Topic perimeter of the right triangle: The perimeter of a right triangle is a fundamental concept in geometry, essential for various applications. This article will guide you through easy steps to calculate it, ensuring a thorough understanding. Whether you're a student, teacher, or enthusiast, you'll find valuable insights and practical tips to master the perimeter of a right triangle.
Table of Content
- Perimeter of a Right Triangle
- Introduction to Right Triangles
- Understanding the Sides of a Right Triangle
- Formula for the Perimeter of a Right Triangle
- Derivation of the Perimeter Formula
- Step-by-Step Calculation of the Perimeter
- Examples of Perimeter Calculation
- Special Cases in Right Triangles
- Applications of Right Triangle Perimeter in Real Life
- Common Mistakes to Avoid
- Practice Problems and Solutions
- YOUTUBE:
Perimeter of a Right Triangle
The perimeter of a right triangle is the total distance around the triangle. It is the sum of the lengths of all three sides. In a right triangle, the sides are commonly referred to as:
- Leg a: One of the two shorter sides
- Leg b: The other shorter side
- Hypotenuse c: The longest side, opposite the right angle
Formula for the Perimeter
The perimeter \( P \) of a right triangle can be calculated using the formula:
\[
P = a + b + c
\]
Using the Pythagorean Theorem
To find the length of the hypotenuse when the lengths of the two legs are known, use the Pythagorean theorem:
\[
c = \sqrt{a^2 + b^2}
\]
Substitute \( c \) back into the perimeter formula:
\[
P = a + b + \sqrt{a^2 + b^2}
\]
Example Calculation
Consider a right triangle with legs \( a = 3 \) units and \( b = 4 \) units.
First, find the hypotenuse \( c \):
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ units}
\]
Then, calculate the perimeter:
\[
P = 3 + 4 + 5 = 12 \text{ units}
\]
Conclusion
The perimeter of a right triangle is a straightforward calculation when the lengths of the sides are known. By using the Pythagorean theorem, even the hypotenuse can be easily determined, allowing for a complete calculation of the perimeter.

READ MORE:
Introduction to Right Triangles
A right triangle is a type of triangle that has one angle measuring 90 degrees. This 90-degree angle is called the right angle. The sides of a right triangle have specific names and properties:
- Legs: The two sides that form the right angle are called the legs. They are typically labeled as \( a \) and \( b \).
- Hypotenuse: The side opposite the right angle is the longest side of the triangle and is called the hypotenuse, labeled as \( c \).
The Pythagorean Theorem is a fundamental principle related to right triangles. It states that:
\[
a^2 + b^2 = c^2
\]
This theorem allows us to calculate the length of any side if the lengths of the other two sides are known. Right triangles are not only fundamental in geometry but also have practical applications in various fields such as construction, navigation, and physics.
Here are some key characteristics and properties of right triangles:
- The sum of the angles in any triangle is 180 degrees. In a right triangle, this includes one right angle and two acute angles.
- The area of a right triangle can be calculated using the formula: \[ \text{Area} = \frac{1}{2} \times a \times b \]
- The perimeter of a right triangle is the sum of the lengths of all three sides: \[ P = a + b + c \]
- Right triangles are often used in trigonometry, where the ratios of their sides define the sine, cosine, and tangent of the acute angles.
Understanding right triangles is crucial for solving many problems in mathematics and science, making them a vital topic in education and practical applications.
Understanding the Sides of a Right Triangle
In a right triangle, the sides have specific names and play unique roles in calculations and properties. These sides are:
- Leg a: One of the two shorter sides that form the right angle.
- Leg b: The other shorter side that forms the right angle.
- Hypotenuse c: The longest side, opposite the right angle.
Each side of a right triangle is essential for various mathematical calculations. Let's explore each side in detail:
- Legs (a and b):
- The legs are perpendicular to each other, meeting at the right angle.
- These sides are used in the Pythagorean Theorem to find the length of the hypotenuse.
- In trigonometry, the legs help define the sine, cosine, and tangent of the angles other than the right angle.
- Hypotenuse (c):
- The hypotenuse is the longest side of the right triangle.
- It is always opposite the right angle.
- The length of the hypotenuse can be found using the Pythagorean Theorem: \[ c = \sqrt{a^2 + b^2} \]
- The hypotenuse is crucial in determining the perimeter of the right triangle.
Using these definitions, we can derive various properties and perform calculations involving right triangles:
- Perimeter: The perimeter of a right triangle is the sum of its three sides: \[ P = a + b + c \]
- Area: The area can be found using the formula: \[ \text{Area} = \frac{1}{2} \times a \times b \]
- Trigonometric Ratios: The ratios of the sides define the sine, cosine, and tangent functions: \[ \sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{a}{c}, \quad \cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{b}{c}, \quad \tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} = \frac{a}{b} \]
Understanding the sides of a right triangle is fundamental for solving various geometric and trigonometric problems, making it an essential topic in mathematics.
Formula for the Perimeter of a Right Triangle
The perimeter of a right triangle is the total distance around the triangle. It is the sum of the lengths of its three sides. In a right triangle, the sides are known as the two legs (\(a\) and \(b\)) and the hypotenuse (\(c\)). To calculate the perimeter, follow these steps:
- Identify the sides: Determine the lengths of the two legs and the hypotenuse. The legs form the right angle, and the hypotenuse is the side opposite the right angle.
- Apply the Pythagorean Theorem: If the length of the hypotenuse is not given, use the Pythagorean Theorem to find it:
\[
c = \sqrt{a^2 + b^2}
\] - Calculate the perimeter: Add the lengths of the three sides using the formula:
\[
P = a + b + c
\]
Let's look at an example to illustrate these steps:
- Example: Suppose we have a right triangle with legs \(a = 3\) units and \(b = 4\) units.
- Step 1: Identify the sides. Here, \(a = 3\) and \(b = 4\).
- Step 2: Apply the Pythagorean Theorem to find the hypotenuse \(c\):
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ units}
\] - Step 3: Calculate the perimeter:
\[
P = 3 + 4 + 5 = 12 \text{ units}
\]
This method ensures that you can accurately determine the perimeter of any right triangle as long as you know the lengths of its sides. Understanding this formula is crucial for solving various geometric problems and applications in real-life scenarios.
Derivation of the Perimeter Formula
The perimeter of a right triangle is derived from the sum of its three sides: the two legs (\(a\) and \(b\)) and the hypotenuse (\(c\)). To understand this derivation step-by-step, follow these steps:
- Identify the Sides:
- Leg \(a\): One of the shorter sides that forms the right angle.
- Leg \(b\): The other shorter side that forms the right angle.
- Hypotenuse \(c\): The longest side, opposite the right angle.
- Use the Pythagorean Theorem: The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs:
\[
c^2 = a^2 + b^2
\] - Solve for the Hypotenuse: To find the length of the hypotenuse, take the square root of both sides of the equation:
\[
c = \sqrt{a^2 + b^2}
\] - Derive the Perimeter Formula: The perimeter (\(P\)) of the right triangle is the sum of the lengths of the three sides:
\[
P = a + b + c
\]Substitute the value of \(c\) from the Pythagorean Theorem:
\p>
\[
P = a + b + \sqrt{a^2 + b^2}
\]
Let's summarize this with an example:
- Example: Suppose we have a right triangle with legs \(a = 5\) units and \(b = 12\) units.
- Step 1: Identify the sides. Here, \(a = 5\) and \(b = 12\).
- Step 2: Apply the Pythagorean Theorem to find the hypotenuse \(c\):
\[
c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \text{ units}
\] - Step 3: Calculate the perimeter:
\[
P = 5 + 12 + 13 = 30 \text{ units}
\]
By understanding the derivation of the perimeter formula, you can accurately calculate the perimeter of any right triangle. This formula is fundamental in geometry and has numerous applications in various fields.

Step-by-Step Calculation of the Perimeter
The perimeter of a right triangle is the sum of the lengths of its three sides: the two legs (\(a\) and \(b\)) and the hypotenuse (\(c\)). Follow these detailed steps to calculate the perimeter of a right triangle:
- Identify the sides:
- Leg \(a\): One of the shorter sides that forms the right angle.
- Leg \(b\): The other shorter side that forms the right angle.
- Hypotenuse \(c\): The longest side, opposite the right angle.
- Apply the Pythagorean Theorem (if needed): If the length of the hypotenuse is not given, use the Pythagorean Theorem to find it:
\[
c = \sqrt{a^2 + b^2}
\] - Calculate the perimeter: Add the lengths of the three sides using the formula:
\[
P = a + b + c
\]
Let's look at an example to illustrate these steps:
- Example: Suppose we have a right triangle with legs \(a = 5\) units and \(b = 12\) units.
- Step 1: Identify the sides. Here, \(a = 5\) and \(b = 12\).
- Step 2: Apply the Pythagorean Theorem to find the hypotenuse \(c\):
\[
c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \text{ units}
\] - Step 3: Calculate the perimeter:
\[
P = 5 + 12 + 13 = 30 \text{ units}
\]
By following these steps, you can accurately determine the perimeter of any right triangle. This method ensures that you include all three sides and apply the correct formulas, providing a comprehensive understanding of the perimeter calculation.
Practice these steps with different sets of values for \(a\) and \(b\) to become proficient in calculating the perimeter of right triangles.
Examples of Perimeter Calculation
To better understand how to calculate the perimeter of a right triangle, let's go through a few detailed examples. These examples will guide you step-by-step through the process.
Example 1
Consider a right triangle with legs \(a = 3\) units and \(b = 4\) units.
- Step 1: Identify the sides. Here, \(a = 3\) and \(b = 4\).
- Step 2: Use the Pythagorean Theorem to find the hypotenuse \(c\):
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ units}
\] - Step 3: Calculate the perimeter:
\[
P = a + b + c = 3 + 4 + 5 = 12 \text{ units}
\]
Example 2
Consider a right triangle with legs \(a = 6\) units and \(b = 8\) units.
- Step 1: Identify the sides. Here, \(a = 6\) and \(b = 8\).
- Step 2: Use the Pythagorean Theorem to find the hypotenuse \(c\):
\[
c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \text{ units}
\] - Step 3: Calculate the perimeter:
\[
P = a + b + c = 6 + 8 + 10 = 24 \text{ units}
\]
Example 3
Consider a right triangle with legs \(a = 7\) units and \(b = 24\) units.
- Step 1: Identify the sides. Here, \(a = 7\) and \(b = 24\).
- Step 2: Use the Pythagorean Theorem to find the hypotenuse \(c\):
\[
c = \sqrt{7^2 + 24^2} = \sqrt{49 + 576} = \sqrt{625} = 25 \text{ units}
\] - Step 3: Calculate the perimeter:
\[
P = a + b + c = 7 + 24 + 25 = 56 \text{ units}
\]
By working through these examples, you can see how the steps to calculate the perimeter of a right triangle are applied. Practice with different values to become more comfortable with the process.
Special Cases in Right Triangles
In geometry, special cases of right triangles often simplify calculations due to their unique properties. Here are some common special cases:
1. Isosceles Right Triangle
An isosceles right triangle has two sides of equal length, which means the two legs are congruent. The properties of an isosceles right triangle include:
- The legs are equal: \(a = b\).
- The hypotenuse can be found using the formula \(c = a\sqrt{2}\).
- The perimeter formula simplifies to \(P = a + a + a\sqrt{2} = 2a + a\sqrt{2}\).
Example Calculation:
If each leg (a) is 5 units, then the hypotenuse (c) is \(5\sqrt{2}\). The perimeter (P) is:
\[ P = 5 + 5 + 5\sqrt{2} = 10 + 5\sqrt{2} \approx 10 + 7.07 = 17.07 \, \text{units} \]
2. 30-60-90 Triangle
A 30-60-90 triangle is another special right triangle where the angles are 30 degrees, 60 degrees, and 90 degrees. The properties of a 30-60-90 triangle include:
- The lengths of the sides are in the ratio \(1:\sqrt{3}:2\).
- If the shorter leg is \(a\), then the longer leg is \(a\sqrt{3}\) and the hypotenuse is \(2a\).
- The perimeter formula is \(P = a + a\sqrt{3} + 2a\).
Example Calculation:
If the shorter leg (a) is 4 units, then the longer leg is \(4\sqrt{3}\) and the hypotenuse is 8 units. The perimeter (P) is:
\[ P = 4 + 4\sqrt{3} + 8 = 12 + 4\sqrt{3} \approx 12 + 6.93 = 18.93 \, \text{units} \]
3. 45-45-90 Triangle
A 45-45-90 triangle is a specific case of an isosceles right triangle where the angles are 45 degrees, 45 degrees, and 90 degrees. Its properties include:
- The legs are equal: \(a = b\).
- The hypotenuse can be found using the formula \(c = a\sqrt{2}\).
- The perimeter formula is \(P = a + a + a\sqrt{2} = 2a + a\sqrt{2}\).
Example Calculation:
If each leg (a) is 3 units, then the hypotenuse (c) is \(3\sqrt{2}\). The perimeter (P) is:
\[ P = 3 + 3 + 3\sqrt{2} = 6 + 3\sqrt{2} \approx 6 + 4.24 = 10.24 \, \text{units} \]
4. Right Triangle with Integer Sides (Pythagorean Triple)
A Pythagorean triple consists of three positive integers \(a\), \(b\), and \(c\) that satisfy the equation \(a^2 + b^2 = c^2\). Common examples include (3, 4, 5) and (5, 12, 13). The properties of a right triangle with integer sides include:
- All sides are integers.
- The hypotenuse and the legs form a Pythagorean triple.
- The perimeter formula is \(P = a + b + c\).
Example Calculation:
If the sides are 3, 4, and 5, the perimeter (P) is:
\[ P = 3 + 4 + 5 = 12 \, \text{units} \]
These special cases make it easier to understand and compute the perimeter of right triangles due to their unique and consistent properties.
Applications of Right Triangle Perimeter in Real Life
The perimeter of a right triangle, which is the sum of the lengths of its three sides, finds practical application in various fields. Here are some key examples:
-
Construction and Architecture
In construction, knowing the perimeter of triangular components helps in determining the amount of materials needed. For example, when framing roofs or creating trusses, the perimeter helps calculate the lengths of timber or metal required.
-
Navigation
In navigation, especially maritime navigation, the principles of right triangles are used to calculate distances and bearings. The perimeter helps in determining the path a ship needs to take, ensuring efficient and safe travel.
-
Surveying
Surveyors use right triangles to measure distances and heights. For example, to find the height of a building, surveyors may measure a baseline on the ground and use the properties of a right triangle. Knowing the perimeter helps in laying out and mapping land accurately.
-
Real Estate and Landscaping
In real estate, the perimeter of plots often needs to be calculated to determine fencing requirements. In landscaping, the perimeter measurement helps in planning the layout and ensuring that garden beds and lawns are appropriately enclosed.
-
Sports and Recreation
Right triangle principles are used in the design and layout of various sports fields and recreational areas. For example, in creating a right-angled running track corner, the perimeter helps in determining the length of the boundary lines and placement of the track.
-
Astronomy and Space Exploration
Astronomers use the properties of right triangles to calculate distances between celestial bodies. For instance, when measuring the distance from Earth to a nearby star, the perimeter of a right triangle can be part of the calculations used to determine such distances accurately.
-
Home Improvement Projects
In DIY projects, calculating the perimeter of right triangular areas is essential for tasks such as tiling, painting, or installing baseboards. For example, when tiling a triangular backsplash, knowing the perimeter helps in purchasing the right amount of materials.
Understanding the perimeter of right triangles is thus crucial in a wide range of practical applications, helping to ensure precision and efficiency in both everyday tasks and professional projects.
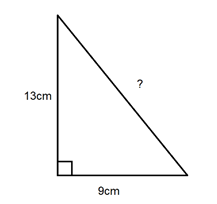
Common Mistakes to Avoid
Calculating the perimeter of a right triangle might seem straightforward, but several common mistakes can lead to incorrect results. Here are some frequent errors and how to avoid them:
- Ignoring the Pythagorean Theorem: When only the lengths of the legs are known, forgetting to use the Pythagorean theorem to find the hypotenuse can result in an incorrect perimeter calculation.
Tip: Always calculate the hypotenuse using \( c = \sqrt{a^2 + b^2} \) when only the legs \( a \) and \( b \) are known.
- Mixing Units: Combining different units of measurement without converting them to a common unit first can lead to errors in the final perimeter.
Tip: Ensure all measurements are in the same unit before performing calculations.
- Rounding Errors: Overly rounding the lengths of sides before the final calculation can significantly affect the accuracy of the perimeter.
Tip: Keep decimal places until the final step to maintain accuracy.
- Forgetting to Add All Sides: A simple but common mistake is forgetting to add all three sides of the triangle when calculating the perimeter.
Tip: Double-check that you've included all three sides in your calculation: \( P = a + b + c \).
- Incorrect Application of Formulas: Misapplying formulas or using the wrong formula altogether can lead to miscalculations.
Tip: Confirm you are using the correct formula for the type of triangle you are dealing with. For right triangles, the perimeter is calculated as \( P = a + b + c \), where \( c \) is the hypotenuse.
Practice Problems and Solutions
Practicing problems on the perimeter of a right triangle helps solidify understanding of the concept and application of the formula. Below are several practice problems along with detailed solutions.
-
Find the perimeter of a right-angled triangle if its base is 6 units, height is 8 units, and hypotenuse is 10 units.
Solution:
Given: base = 6 units, height = 8 units, hypotenuse = 10 units.
The perimeter of the right-angled triangle is calculated by adding all the sides:
\[
\text{Perimeter} = 6 + 8 + 10 = 24 \text{ units}
\] -
In a right-angled triangle, if the base is 5 units and the height is 12 units, find its perimeter.
Solution:
Given: base = 5 units, height = 12 units.
First, calculate the hypotenuse using the Pythagorean theorem:
\[
\text{Hypotenuse}^2 = 5^2 + 12^2 = 25 + 144 = 169
\]\[
\text{Hypotenuse} = \sqrt{169} = 13 \text{ units}
\]Then, find the perimeter:
\[
\text{Perimeter} = 5 + 12 + 13 = 30 \text{ units}
\] -
A right-angled triangle has a hypotenuse of 15 units and one of the legs is 9 units. Find the perimeter.
Solution:
Given: hypotenuse = 15 units, one leg = 9 units.
First, calculate the other leg using the Pythagorean theorem:
\[
\text{Hypotenuse}^2 = \text{Leg}_1^2 + \text{Leg}_2^2
\]\[
15^2 = 9^2 + \text{Leg}_2^2
\]\[
225 = 81 + \text{Leg}_2^2
\]\[
\text{Leg}_2^2 = 144
\]\[
\text{Leg}_2 = \sqrt{144} = 12 \text{ units}
\]Then, find the perimeter:
\[
\text{Perimeter} = 9 + 12 + 15 = 36 \text{ units}
\]
These practice problems cover various scenarios involving the perimeter of right triangles. Ensure to use the Pythagorean theorem where necessary and remember the perimeter is the sum of all three sides.
Diện Tích và Chu Vi của Tam Giác Vuông | Toán Học với Thầy J
READ MORE:
Cách Tinh Tế để Tìm Chu Vi của Tam Giác Vuông | (giải thích từng bước) | #toánhọc #toán