Topic perimeter right angle triangle: Discover the simple steps to calculate the perimeter of a right angle triangle. This guide will help you understand the formula, apply the Pythagorean theorem, and solve problems with ease. Perfect for students, teachers, and anyone interested in geometry, this article breaks down the process into easy-to-follow instructions.
Table of Content
- Perimeter of a Right Angle Triangle
- Introduction to Right Angle Triangles
- Definition and Properties
- Understanding the Perimeter
- Pythagorean Theorem
- Step-by-Step Calculation
- Examples of Perimeter Calculation
- Pythagorean Triples
- Special Cases and Triangles
- Applications in Real Life
- Common Mistakes to Avoid
- Practice Problems
- Summary and Conclusion
- YOUTUBE:
Perimeter of a Right Angle Triangle
The perimeter of a right angle triangle can be calculated by summing the lengths of its three sides. A right angle triangle consists of two legs and a hypotenuse, where the hypotenuse is the longest side opposite the right angle.
Formula for the Perimeter
The formula for the perimeter \( P \) of a right angle triangle with legs \( a \) and \( b \) and hypotenuse \( c \) is given by:
\[ P = a + b + c \]
Using the Pythagorean Theorem
To find the hypotenuse \( c \), we use the Pythagorean theorem:
\[ c = \sqrt{a^2 + b^2} \]
Substituting this into the perimeter formula, we get:
\[ P = a + b + \sqrt{a^2 + b^2} \]
Example Calculation
Consider a right angle triangle with legs \( a = 3 \) and \( b = 4 \):
- Calculate the hypotenuse: \( c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \)
- Calculate the perimeter: \( P = 3 + 4 + 5 = 12 \)
Special Cases
There are certain right angle triangles, known as Pythagorean triples, where the lengths of the sides are all integers. Some common examples include:
- \( (3, 4, 5) \)
- \( (5, 12, 13) \)
- \( (7, 24, 25) \)
Applications
The concept of the perimeter of a right angle triangle is used in various applications including:
- Construction and architecture
- Navigation and mapping
- Trigonometry and geometry problems
Understanding the perimeter helps in solving real-world problems where right angle triangles are involved.

READ MORE:
Introduction to Right Angle Triangles
A right angle triangle is a type of triangle that has one angle equal to 90 degrees. This special characteristic defines its geometric properties and applications. Here, we will explore the fundamental aspects of right angle triangles and their significance in geometry.
The right angle triangle is defined by three main features:
- Right Angle: One of the angles is exactly 90 degrees.
- Legs: The two sides that form the right angle are called the legs. They are usually denoted as \(a\) and \(b\).
- Hypotenuse: The side opposite the right angle is the longest side of the triangle and is called the hypotenuse, denoted as \(c\).
In a right angle triangle, the sides and angles have specific relationships that can be described using the Pythagorean theorem:
\[ c^2 = a^2 + b^2 \]
This theorem states that the square of the length of the hypotenuse (\(c\)) is equal to the sum of the squares of the lengths of the other two sides (\(a\) and \(b\)).
Right angle triangles are crucial in various fields due to their unique properties. Some of their applications include:
- Trigonometry: Fundamental in defining sine, cosine, and tangent functions.
- Construction and Engineering: Essential in designing buildings, bridges, and various structures.
- Navigation: Used in map-making and locating positions.
Understanding the basics of right angle triangles is the first step in delving into more complex geometric concepts and solving real-world problems involving these shapes.
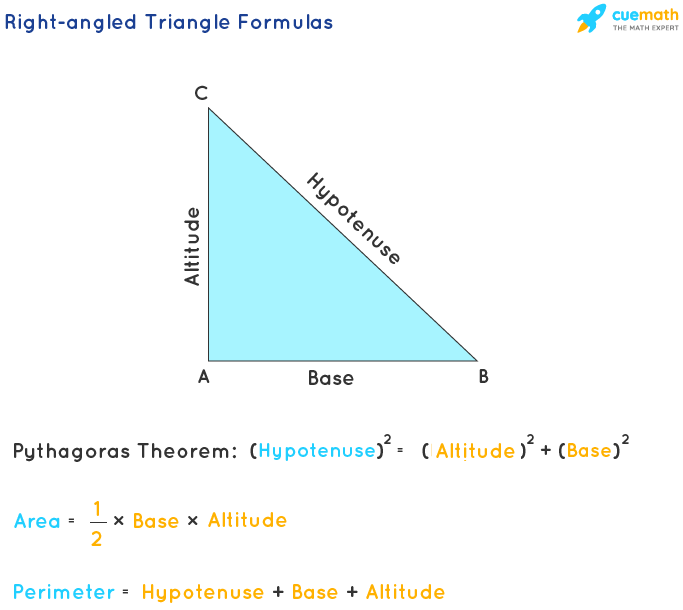
Definition and Properties
A right angle triangle, also known as a right-angled triangle, is a triangle in which one of the angles is a right angle (90 degrees). This unique feature influences the properties and relationships between the sides and angles of the triangle.
The main components of a right angle triangle are:
- Right Angle: One of the angles is exactly 90 degrees, which defines the triangle.
- Legs: The two sides that form the right angle are called the legs. They are typically labeled as \(a\) and \(b\).
- Hypotenuse: The side opposite the right angle is the longest side of the triangle and is referred to as the hypotenuse, labeled as \(c\).
The properties of a right angle triangle include:
- Pythagorean Theorem: This fundamental property states that the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides: \[ c^2 = a^2 + b^2 \]
- Perimeter: The perimeter of a right angle triangle is the sum of the lengths of all three sides. It can be calculated using the formula: \[ P = a + b + c \]
- Area: The area of a right angle triangle is given by half the product of the lengths of the two legs: \[ \text{Area} = \frac{1}{2} \times a \times b \]
- Trigonometric Ratios: The sides of a right angle triangle are related through trigonometric ratios such as sine, cosine, and tangent: \[ \sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}, \quad \cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}}, \quad \tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} \]
Right angle triangles are integral to various mathematical concepts and real-world applications. Their unique properties make them essential in trigonometry, geometry, engineering, and physics.
Understanding the Perimeter
The perimeter of a right-angle triangle is the total distance around the triangle. To understand the perimeter, let's break it down step by step:
A right-angle triangle consists of three sides:
- The two legs (also called the perpendicular sides) which form the right angle.
- The hypotenuse, which is the side opposite the right angle and the longest side of the triangle.
To calculate the perimeter of a right-angle triangle, you need to know the lengths of all three sides. The perimeter is simply the sum of these lengths. The formula for the perimeter \( P \) of a right-angle triangle with legs \( a \) and \( b \), and hypotenuse \( c \) is:
Formula:
\[ P = a + b + c \]
Let's consider an example to illustrate this:
- Identify the lengths of the two legs, \( a \) and \( b \).
- Use the Pythagorean theorem to find the length of the hypotenuse \( c \): \[ c = \sqrt{a^2 + b^2} \]
- Add the lengths of all three sides to find the perimeter: \[ P = a + b + c \]
For instance, if the lengths of the legs are \( a = 3 \) units and \( b = 4 \) units:
- Calculate the hypotenuse: \[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Calculate the perimeter: \[ P = 3 + 4 + 5 = 12 \] units
In summary, the perimeter of a right-angle triangle is determined by summing the lengths of its three sides. Understanding this concept is essential for solving various problems related to right-angle triangles in geometry.
Pythagorean Theorem
The Pythagorean Theorem is a fundamental principle in geometry, specifically for right-angled triangles. This theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
This relationship can be expressed with the formula:
\[ c^2 = a^2 + b^2 \]
where:
- c is the length of the hypotenuse
- a and b are the lengths of the other two sides
To apply the Pythagorean Theorem, follow these steps:
- Identify the lengths of the two legs (a and b) of the right triangle.
- Square both lengths: \(a^2\) and \(b^2\).
- Add the squares together: \(a^2 + b^2\).
- Take the square root of the sum to find the length of the hypotenuse: \(\sqrt{a^2 + b^2} = c\).
For example, if a right-angled triangle has legs of lengths 3 and 4 units, the length of the hypotenuse can be calculated as follows:
- Square the lengths of the legs: \(3^2 = 9\) and \(4^2 = 16\).
- Add the squares: \(9 + 16 = 25\).
- Take the square root of the sum: \(\sqrt{25} = 5\).
Thus, the hypotenuse has a length of 5 units.
The Pythagorean Theorem is not only crucial for geometric calculations but also has applications in various fields such as physics, engineering, computer science, and many real-life scenarios where distances and measurements are involved.

Step-by-Step Calculation
Calculating the perimeter of a right-angle triangle involves determining the lengths of all three sides and then summing them up. Here is a detailed step-by-step guide:
-
Identify the lengths of the sides: In a right-angle triangle, the sides are usually referred to as the base (a), the height (b), and the hypotenuse (c). The hypotenuse is the side opposite the right angle.
-
Use the Pythagorean Theorem if necessary: If only the lengths of the base and height are known, use the Pythagorean Theorem to find the hypotenuse:
\[
c = \sqrt{a^2 + b^2}
\] -
Sum the lengths of all three sides: Once all sides are known, add them together to find the perimeter (P):
\[
P = a + b + c
\]
Example Calculation
Consider a right-angle triangle with a base of 3 units, a height of 4 units, and a hypotenuse of 5 units. Follow these steps to calculate the perimeter:
-
Given:
- Base (a) = 3 units
- Height (b) = 4 units
- Hypotenuse (c) = 5 units
-
Calculate the hypotenuse using the Pythagorean Theorem:
Since the hypotenuse is already given as 5 units, we can confirm it by:
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\] -
Find the perimeter:
\[
P = 3 + 4 + 5 = 12 \text{ units}
\]
Therefore, the perimeter of the right-angle triangle is 12 units.
Additional Example
Consider another right-angle triangle where the base is 5 units, and the hypotenuse is 13 units. The steps to find the perimeter are:
-
Given:
- Base (a) = 5 units
- Hypotenuse (c) = 13 units
- Height (b) = ? (unknown)
-
Calculate the height using the Pythagorean Theorem:
\[
b = \sqrt{c^2 - a^2} = \sqrt{13^2 - 5^2} = \sqrt{169 - 25} = \sqrt{144} = 12 \text{ units}
\] -
Find the perimeter:
\[
P = 5 + 13 + 12 = 30 \text{ units}
\]
Hence, the perimeter of this right-angle triangle is 30 units.
Examples of Perimeter Calculation
Calculating the perimeter of a right-angled triangle involves summing the lengths of its three sides: the base (a), the height (b), and the hypotenuse (c). Here are some examples to illustrate the process:
Example 1
Find the perimeter of a right triangle with sides of length 6 cm, 8 cm, and 10 cm.
- Identify the sides:
- Base (a) = 6 cm
- Height (b) = 8 cm
- Hypotenuse (c) = 10 cm
- Apply the perimeter formula: \( P = a + b + c \)
- Calculate the perimeter:
\( P = 6 + 8 + 10 = 24 \) cm
Example 2
Calculate the perimeter of a right triangle with a base of 5 m and a height of 12 m.
- Find the hypotenuse using the Pythagorean theorem:
\( c = \sqrt{a^2 + b^2} = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \) m
- Apply the perimeter formula: \( P = a + b + c \)
- Calculate the perimeter:
\( P = 5 + 12 + 13 = 30 \) m
Example 3
Determine the perimeter of a right triangle with a height of 9 m and a hypotenuse of 15 m.
- Find the base using the Pythagorean theorem:
\( b = \sqrt{c^2 - a^2} = \sqrt{15^2 - 9^2} = \sqrt{225 - 81} = \sqrt{144} = 12 \) m
- Apply the perimeter formula: \( P = a + b + c \)
- Calculate the perimeter:
\( P = 9 + 12 + 15 = 36 \) m
Example 4
Find the perimeter of a right triangle where the lengths of the two legs are 7 m and 24 m.
- Find the hypotenuse using the Pythagorean theorem:
\( c = \sqrt{a^2 + b^2} = \sqrt{7^2 + 24^2} = \sqrt{49 + 576} = \sqrt{625} = 25 \) m
- Apply the perimeter formula: \( P = a + b + c \)
- Calculate the perimeter:
\( P = 7 + 24 + 25 = 56 \) m
Example 5
Calculate the perimeter of a right triangle with side lengths of 11 cm, 12 cm, and 16.28 cm.
- Identify the sides:
- Base (a) = 11 cm
- Height (b) = 12 cm
- Hypotenuse (c) = 16.28 cm
- Apply the perimeter formula: \( P = a + b + c \)
- Calculate the perimeter:
\( P = 11 + 12 + 16.28 = 39.28 \) cm
These examples show how to apply the Pythagorean theorem and perimeter formula to calculate the perimeter of right-angled triangles. Practice with different sets of given sides to become proficient in these calculations.
Pythagorean Triples
Pythagorean triples are sets of three positive integers \(a\), \(b\), and \(c\) that satisfy the equation \(a^2 + b^2 = c^2\). These triples represent the side lengths of right-angled triangles, where \(c\) is the hypotenuse, and \(a\) and \(b\) are the other two sides. Pythagorean triples can be classified into primitive and non-primitive triples.
Primitive Pythagorean Triples
Primitive Pythagorean triples are sets of three integers that are coprime (i.e., their greatest common divisor is 1). Examples of primitive Pythagorean triples include:
- (3, 4, 5)
- (5, 12, 13)
- (7, 24, 25)
- (9, 40, 41)
Non-Primitive Pythagorean Triples
Non-primitive Pythagorean triples are multiples of primitive triples. For instance, multiplying the primitive triple (3, 4, 5) by 2 yields the non-primitive triple (6, 8, 10). Examples include:
- (6, 8, 10)
- (9, 12, 15)
- (12, 16, 20)
Generating Pythagorean Triples
Pythagorean triples can be generated using formulas, especially for primitive triples:
- For any two positive integers \(m\) and \(n\) with \(m > n\):
- \(a = m^2 - n^2\)
- \(b = 2mn\)
- \(c = m^2 + n^2\)
For example, if \(m = 3\) and \(n = 2\), then:
- \(a = 3^2 - 2^2 = 9 - 4 = 5\)
- \(b = 2 \times 3 \times 2 = 12\)
- \(c = 3^2 + 2^2 = 9 + 4 = 13\)
Examples and Verification
Here are some examples of Pythagorean triples along with their verification:
- Example 1: (3, 4, 5)
- Verification: \(3^2 + 4^2 = 9 + 16 = 25 = 5^2\)
- Example 2: (5, 12, 13)
- Verification: \(5^2 + 12^2 = 25 + 144 = 169 = 13^2\)
- Example 3: (8, 15, 17)
- Verification: \(8^2 + 15^2 = 64 + 225 = 289 = 17^2\)
Special Properties
- Every primitive Pythagorean triple has one odd and one even number.
- The hypotenuse in primitive triples is always odd.
- Scaling a primitive triple by any positive integer yields a non-primitive triple.
Applications
Pythagorean triples are useful in various fields including geometry, number theory, and real-life applications like construction and navigation, where right-angled triangles are common.
Special Cases and Triangles
Right-angled triangles have unique properties, and among them, some special cases stand out due to their consistent side ratios and properties. Understanding these special triangles can simplify many geometric calculations.
30°-60°-90° Triangle
This triangle is characterized by its angles of 30°, 60°, and 90°. The sides of this triangle are in a consistent ratio of 1:√3:2. This means:
- The side opposite the 30° angle is the shortest and is denoted as \( x \).
- The side opposite the 60° angle is \( x\sqrt{3} \).
- The hypotenuse (opposite the 90° angle) is \( 2x \).
For example, if the shortest side \( x \) is 3 units, the other sides will be:
- Side opposite 60°: \( 3\sqrt{3} \) units
- Hypotenuse: \( 6 \) units
45°-45°-90° Triangle
This triangle has two 45° angles and one 90° angle, making it an isosceles right triangle. The sides are in a ratio of 1:1:√2. This means:
- The legs opposite the 45° angles are equal, denoted as \( x \).
- The hypotenuse is \( x\sqrt{2} \).
For instance, if each leg \( x \) is 5 units, the hypotenuse will be:
- Hypotenuse: \( 5\sqrt{2} \) units
Pythagorean Triples
Pythagorean triples are sets of three integers that satisfy the Pythagorean theorem \( a^2 + b^2 = c^2 \). These triples are special because they represent the side lengths of right-angled triangles with integer values.
- Common Pythagorean Triples: Examples include (3, 4, 5), (5, 12, 13), and (8, 15, 17).
- Almost-isosceles Pythagorean Triples: These triples are nearly isosceles, such as (20, 21, 29) and (119, 120, 169).
- Pythagorean Triples in Geometric Progression: Known as Kepler triangles, their sides are in geometric progression, such as (1, φ, φ²) where φ is the golden ratio.
Special right triangles are incredibly useful in various geometric problems, as their fixed ratios and properties can make calculations more straightforward and efficient.

Applications in Real Life
Right-angled triangles have numerous practical applications in various fields. These applications are often related to the calculation of distances, heights, and angles. Below are some examples of how right-angled triangles are used in real life:
1. Architecture and Construction
In architecture, right-angled triangles are used to ensure the structural integrity and proper alignment of buildings.
- Finding the height of a building using trigonometric ratios.
- Ensuring that walls are perpendicular to the ground.
- Determining the length of roof rafters using the Pythagorean theorem.
2. Navigation
Navigation relies heavily on the principles of right-angled triangles for determining distances and plotting courses.
- Calculating the distance between two points using the horizontal and vertical components.
- Determining the position of a ship relative to the shore.
- Using angles of elevation and depression to navigate through hilly terrains.
3. Surveying
Surveyors use right-angled triangles to measure land and determine distances.
- Estimating the height of a structure using a total station theodolite.
- Calculating distances between various points on a plot of land.
4. Astronomy
Right-angled triangles help astronomers calculate distances and angles in space.
- Determining the distance between stars using parallax methods.
- Calculating the height of an astronomical object above the horizon.
5. Carpentry
Carpenters frequently use right-angled triangles to ensure their projects are level and square.
- Creating right angles for furniture and framing.
- Measuring and cutting materials at precise angles.
6. Aviation
Pilots and air traffic controllers use right-angled triangles for navigation and ensuring flight safety.
- Calculating the angle of descent for landing.
- Determining the distance between the aircraft and the runway.
7. Engineering
Engineers use right-angled triangles in various calculations related to design and analysis.
- Designing mechanical parts that require precise angular measurements.
- Analyzing forces and stresses in structures.
8. Everyday Applications
Right-angled triangles are also used in everyday activities.
- Using a ladder safely against a wall.
- Estimating the height of an object by measuring its shadow.
- Creating art and design projects that require precise measurements.
Common Mistakes to Avoid
Calculating the perimeter of a right-angle triangle can be straightforward, but there are several common mistakes that can lead to errors. Here are some of the most frequent mistakes and tips on how to avoid them:
-
Misidentifying the Sides:
One common mistake is confusing the sides of the triangle, especially the hypotenuse (the longest side opposite the right angle) with the legs.
Tip: Always label each side clearly and double-check their lengths before starting any calculations.
-
Incorrect Use of the Pythagorean Theorem:
Some students mistakenly apply the Pythagorean theorem to non-right triangles or use incorrect values.
Tip: Remember, the Pythagorean theorem (\(a^2 + b^2 = c^2\)) only applies to right triangles. Ensure you are working with a right-angle triangle before using this formula.
-
Arithmetic Errors:
Simple addition mistakes can lead to incorrect perimeter values.
Tip: Perform each calculation step carefully, and consider using a calculator to minimize errors.
-
Units of Measurement:
Failing to convert all measurements to the same unit can lead to incorrect results.
Tip: Ensure all side lengths are in the same unit before performing any calculations.
-
Rounding Errors:
Rounding too early in calculations can lead to significant errors in the final perimeter.
Tip: Keep calculations as precise as possible and only round off the final result if necessary.
-
Not Verifying Results:
Students often skip the step of verifying their results, leading to unchecked errors.
Tip: Always review your calculations to ensure accuracy. Cross-check your results with different methods if possible.
Avoiding these common mistakes can greatly improve the accuracy of your calculations. Always approach problems methodically and double-check your work for the best results.
Practice Problems
Here are some practice problems to help you understand how to calculate the perimeter of a right-angled triangle. Use the Pythagorean theorem and the perimeter formula to solve these problems.
-
Find the perimeter of a right-angled triangle with the following sides:
- Base: 6 units
- Height: 8 units
Solution:
- Calculate the hypotenuse using the Pythagorean theorem:
\( \text{Hypotenuse}^2 = \text{Base}^2 + \text{Height}^2 \)
\( \text{Hypotenuse}^2 = 6^2 + 8^2 \)
\( \text{Hypotenuse}^2 = 36 + 64 \)
\( \text{Hypotenuse} = \sqrt{100} = 10 \) units - Find the perimeter:
\( \text{Perimeter} = \text{Base} + \text{Height} + \text{Hypotenuse} \)
\( \text{Perimeter} = 6 + 8 + 10 = 24 \) units
-
Determine the perimeter of a right-angled triangle with the following sides:
- Base: 5 units
- Hypotenuse: 13 units
Solution:
- Calculate the height using the Pythagorean theorem:
\( \text{Hypotenuse}^2 = \text{Base}^2 + \text{Height}^2 \)
\( 13^2 = 5^2 + \text{Height}^2 \)
\( 169 = 25 + \text{Height}^2 \)
\( \text{Height}^2 = 144 \)
\( \text{Height} = \sqrt{144} = 12 \) units - Find the perimeter:
\( \text{Perimeter} = \text{Base} + \text{Height} + \text{Hypotenuse} \)
\( \text{Perimeter} = 5 + 12 + 13 = 30 \) units
-
Calculate the perimeter of a right-angled triangle where:
- Base: 9 units
- Height: 12 units
Solution:
- Calculate the hypotenuse using the Pythagorean theorem:
\( \text{Hypotenuse}^2 = \text{Base}^2 + \text{Height}^2 \)
\( \text{Hypotenuse}^2 = 9^2 + 12^2 \)
\( \text{Hypotenuse}^2 = 81 + 144 \)
\( \text{Hypotenuse} = \sqrt{225} = 15 \) units - Find the perimeter:
\( \text{Perimeter} = \text{Base} + \text{Height} + \text{Hypotenuse} \)
\( \text{Perimeter} = 9 + 12 + 15 = 36 \) units
-
Find the perimeter of a right-angled triangle with sides of lengths:
- 8 units,
- 15 units,
- 17 units.
Solution:
The given sides already form a right-angled triangle (8, 15, 17 is a Pythagorean triple). The perimeter is calculated as follows:
- \( \text{Perimeter} = 8 + 15 + 17 = 40 \) units
Use these practice problems to improve your understanding of calculating the perimeter of right-angled triangles. Remember to always check your calculations carefully.
Summary and Conclusion
In this article, we have explored the concept of the perimeter of a right-angled triangle in depth. We started with an introduction to right-angled triangles, defining them and outlining their key properties. A right-angled triangle is characterized by one angle being exactly 90 degrees, with the sides adjacent to this angle referred to as the base and the height, and the side opposite the right angle known as the hypotenuse.
We learned that the perimeter of a right-angled triangle is the sum of the lengths of all its sides. This can be expressed with the formula:
\[
\text{Perimeter} = a + b + c
\]
where \(a\) and \(b\) are the legs of the triangle and \(c\) is the hypotenuse.
We also discussed the Pythagorean Theorem, a crucial principle for calculating the hypotenuse when the lengths of the other two sides are known. The theorem is stated as:
\[
c^2 = a^2 + b^2
\]
Using this theorem, one can determine the length of the hypotenuse, which is then used to calculate the perimeter.
Key Takeaways
- The perimeter of a right-angled triangle is the total length around the triangle, calculated by adding the lengths of its three sides.
- The Pythagorean Theorem is essential for finding the hypotenuse when only the base and height are known.
- Practical applications of calculating the perimeter include fields such as construction, navigation, and various engineering disciplines.
- Common mistakes to avoid include incorrect application of the Pythagorean Theorem and incorrect summation of the side lengths.
By mastering these concepts, you can accurately determine the perimeter of any right-angled triangle, a fundamental skill in geometry and its numerous real-world applications. Practice with various problems and scenarios to solidify your understanding and proficiency.
Diện Tích và Chu Vi của Tam Giác Vuông | Toán với Thầy J
READ MORE:
Cách Tinh Tế để Tìm Chu Vi của Tam Giác Vuông | (giải thích từng bước) | #toán #toán học