Topic perimeter of an oval: Understanding the perimeter of an oval, or ellipse, is essential for various mathematical and practical applications. This guide explores different methods to calculate the perimeter, including Ramanujan's approximations, numerical integration, and series expansions, offering both accuracy and simplicity. Dive in to enhance your knowledge and application of these fascinating geometric shapes.
Table of Content
- Perimeter of an Oval
- Introduction to Ovals and Ellipses
- Mathematical Definition of an Oval
- Basic Properties of Ellipses
- Methods to Calculate the Perimeter of an Oval
- Ramanujan's Approximations
- Using Numerical Integration
- Series Expansion Methods
- Elliptic Integral Approach
- Comparison of Different Methods
- Applications of Perimeter Calculations
- Practical Examples and Exercises
- Conclusion and Further Reading
- YOUTUBE: Hướng dẫn cách tính diện tích và chu vi của sân hình bầu dục để thu hút người xem và đảm bảo chính tả đúng.
Perimeter of an Oval
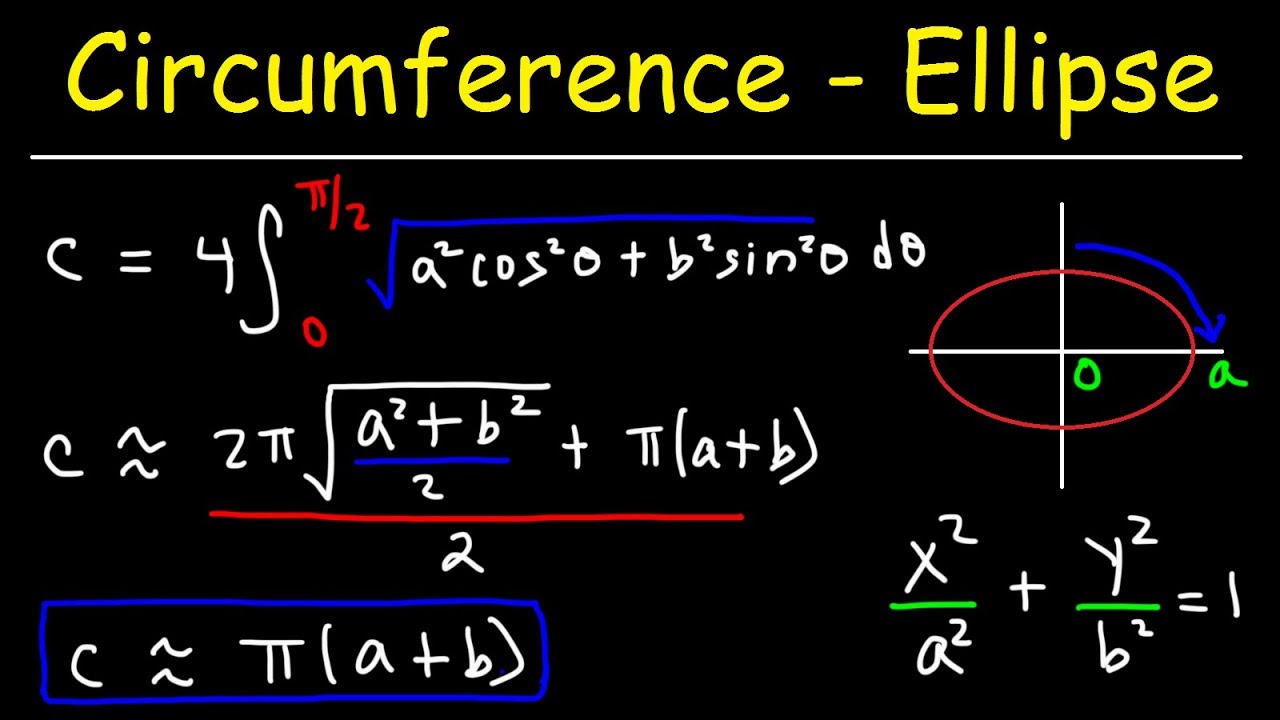
An oval, commonly referred to as an ellipse in mathematics, has a perimeter that is not as straightforward to calculate as that of a circle or rectangle. The perimeter (P) of an ellipse with semi-major axis \(a\) and semi-minor axis \(b\) does not have a simple exact formula but can be approximated by several methods.
Approximation Methods
Here are some commonly used approximation formulas for the perimeter of an ellipse:
- Ramanujan's Approximation:
Ramanujan provided two popular approximations for the perimeter of an ellipse:
- \( P \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right] \)
- \( P \approx \pi \left( a + b \right) \left( 1 + \frac{3h}{10 + \sqrt{4 - 3h}} \right) \)
where \( h = \frac{(a - b)^2}{(a + b)^2} \).
- Numerical Integration:
The perimeter can be computed more accurately using numerical methods. For example:
The complete elliptic integral of the second kind \( E(e) \) can be used, where \( e = \sqrt{1 - \frac{b^2}{a^2}} \) is the eccentricity:
\( P \approx 4a E(e) \)
In this formula, \( E(e) \) is evaluated using numerical methods, making it more complex but accurate.
- Series Expansion:
Another method involves using an infinite series:
\( P \approx \pi (a + b) \left( 1 + \sum_{n=1}^{\infty} \left( \frac{(2n-1)!!}{(2n)!!} \right)^2 \left( \frac{(a-b)^2}{(a+b)^2} \right)^n \right) \)
Here, \( (2n-1)!! \) denotes the double factorial of an odd number, and \( (2n)!! \) denotes the double factorial of an even number.
Conclusion
While there is no simple formula for the exact perimeter of an ellipse, the approximations provided by Ramanujan and other methods give sufficiently accurate results for practical purposes. For highly precise calculations, numerical methods involving elliptic integrals are recommended.

READ MORE:
Introduction to Ovals and Ellipses
An oval, often referred to as an ellipse in mathematical terms, is a smooth, closed curve that resembles the shape of an egg. Ellipses are a specific type of conic section, formed by the intersection of a plane with a cone at an angle that is not perpendicular to the cone's base.
Ellipses have two main axes: the major axis, which is the longest diameter, and the minor axis, which is the shortest diameter. These axes intersect at the center of the ellipse, dividing it into four equal parts.
Some basic properties of ellipses include:
- Foci: Ellipses have two focal points (foci). The sum of the distances from any point on the ellipse to the two foci is constant.
- Eccentricity: The eccentricity of an ellipse, denoted as \(e\), is a measure of how much the ellipse deviates from being a circle. It ranges between 0 (a circle) and 1 (a highly elongated ellipse).
- Major and Minor Axes: The longest diameter of the ellipse is the major axis, and the shortest diameter is the minor axis.
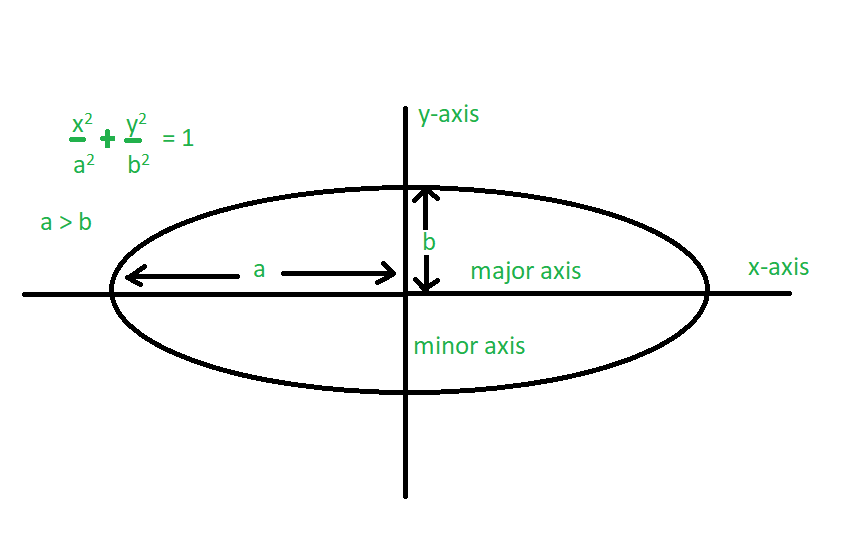
Mathematically, an ellipse can be defined by its equation in Cartesian coordinates:
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
Here, \(a\) is the length of the semi-major axis, and \(b\) is the length of the semi-minor axis.
Ellipses appear in various real-world applications, such as planetary orbits, the design of optical systems, and architectural structures.
Mathematical Definition of an Oval
An oval is a broad term that describes any closed, convex curve resembling the shape of an egg. Unlike a circle or an ellipse, an oval does not have a precise mathematical definition and may not exhibit symmetry along its axes.
The term "oval" comes from the Latin word ovum, meaning egg. This curve can take various forms, including:
- Curves with a single axis of symmetry.
- Shapes that do not significantly deviate from an elliptical form.
- Any differentiable, convex, closed plane curve.
In a more formal geometric context, an oval often refers to:
- Cassini ovals
- Superellipses
- Stadium shapes
- Cartesian ovals
Ellipses, which are a specific type of oval, have two principal axes of symmetry: the major axis and the minor axis. An ellipse is defined by the equation:
\[
\left(\frac{x}{a}\right)^2 + \left(\frac{y}{b}\right)^2 = 1
\]
where \(a\) and \(b\) are the lengths of the semi-major and semi-minor axes, respectively.
To distinguish between general ovals and ellipses:
- All ellipses are ovals, but not all ovals are ellipses.
- Ellipses are symmetrical about both the major and minor axes, whereas ovals may not exhibit this symmetry.
In practical applications, such as technical drawing or architecture, various methods are used to construct ovals, such as using a compass and ruler or a rubber band.
In summary, while ovals and ellipses share similarities, the term "oval" encompasses a broader range of shapes, making it less rigidly defined in mathematical terms compared to an ellipse.
Basic Properties of Ellipses
An ellipse is a fundamental geometric shape characterized by its unique properties and structure. Here are some of the key properties of ellipses:
- Definition: An ellipse is defined as the set of all points in a plane such that the sum of the distances to two fixed points, called foci, is constant. Mathematically, for any point \( P \) on the ellipse, the distances \( d_1 \) and \( d_2 \) to the foci satisfy the equation \( d_1 + d_2 = \text{constant} \).
- Axes:
- Major Axis: The longest diameter of the ellipse, passing through both foci. The endpoints of the major axis are called vertices.
- Minor Axis: The shortest diameter of the ellipse, perpendicular to the major axis at the center. The endpoints of the minor axis are co-vertices.
- Semi-Major and Semi-Minor Axes:
- Semi-Major Axis (a): Half of the major axis.
- Semi-Minor Axis (b): Half of the minor axis.
- Relationship Between Axes and Foci: The distance between the center of the ellipse and each focus is denoted by \( c \). This distance is related to the semi-major and semi-minor axes by the equation \( c^2 = a^2 - b^2 \).
- Equation of an Ellipse:
The standard form of the equation of an ellipse with center at \( (h, k) \) is:
- For a horizontal major axis: \(\frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} = 1\)
- For a vertical major axis: \(\frac{(x - h)^2}{b^2} + \frac{(y - k)^2}{a^2} = 1\)
If the center is at the origin (0, 0), the equations simplify to:
- Horizontal major axis: \(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\)
- Vertical major axis: \(\frac{x^2}{b^2} + \frac{y^2}{a^2} = 1\)
- Parametric Form:
The parametric equations for an ellipse centered at \( (h, k) \) are:
- For a horizontal major axis: \( x = h + a \cos(\theta) \), \( y = k + b \sin(\theta) \)
- For a vertical major axis: \( x = h + b \cos(\theta) \), \( y = k + a \sin(\theta) \)
- Eccentricity (e):
The eccentricity of an ellipse is a measure of its "ovalness" and is given by \( e = \frac{c}{a} \), where \( c \) is the distance from the center to a focus and \( a \) is the length of the semi-major axis. The eccentricity ranges from 0 (a circle) to almost 1 (a highly elongated ellipse).
- Area:
The area of an ellipse is given by the formula:
\( A = \pi \cdot a \cdot b \)
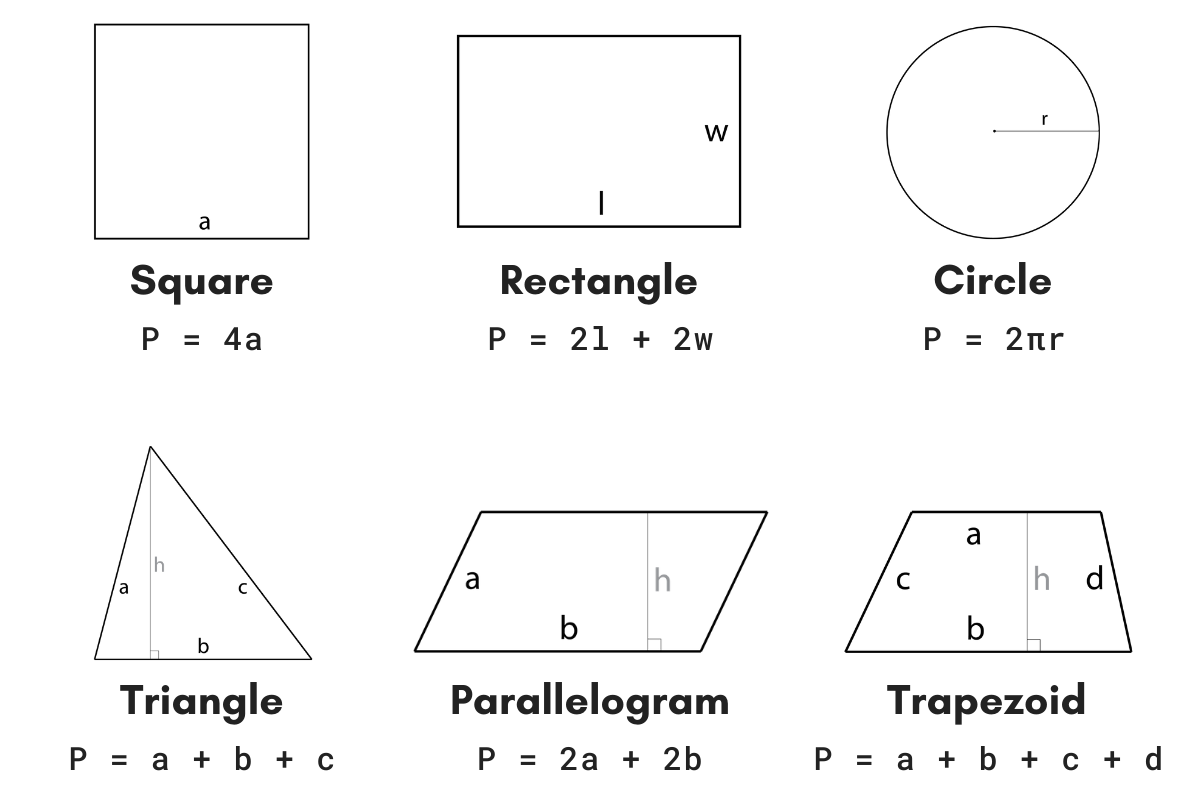
Methods to Calculate the Perimeter of an Oval
The perimeter of an oval, often referred to as an ellipse, cannot be determined using a simple formula like that of a circle. However, there are several methods to approximate the perimeter with varying degrees of accuracy. Here are the most common methods:
-
Naive Formula:
This is the simplest approximation and is given by:
\(P = \pi (a + b)\)
where \(a\) is the length of the semi-major axis and \(b\) is the length of the semi-minor axis. This formula is easy to use but may not be very accurate for ellipses with high eccentricity.
-
Ramanujan's Approximation:
Ramanujan provided a more accurate approximation formula:
\(P \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right]\)
This formula is generally more accurate than the naive formula, especially for ellipses that are not too elongated.
-
Exact Integral Form:
The exact perimeter of an ellipse can be expressed as an elliptic integral:
\(P = 4a \int_{0}^{\pi/2} \sqrt{1 - e^2 \sin^2 \theta} \, d\theta\)
where \(e\) is the eccentricity of the ellipse, defined as \(e = \sqrt{1 - \frac{b^2}{a^2}}\). This integral does not have a simple closed-form solution and typically requires numerical methods to evaluate.
-
Series Expansion Methods:
These methods involve expanding the integral into a series and summing the terms to the desired accuracy. One such series expansion is:
\(P \approx \pi (a + b) \left[1 + \sum_{n=1}^{\infty} \left( \frac{(2n-1)!!}{(2n)!!} \right)^2 \left( \frac{a - b}{a + b} \right)^{2n} \right]\)
where \((2n-1)!!\) is the double factorial.
These methods offer a range of approaches depending on the required accuracy and computational resources available. For practical purposes, the naive and Ramanujan's approximations are often sufficient, while the exact integral and series expansion methods are used for more precise calculations.
Ramanujan's Approximations
Srinivasa Ramanujan, an Indian mathematician, developed several approximations for calculating the perimeter of an ellipse, which are particularly valuable due to the complexity of the exact calculation.
Ramanujan provided two notable approximations for the perimeter \( P \) of an ellipse with semimajor axis \( a \) and semiminor axis \( b \):
- First Approximation:
This simpler form is given by:
\[
P \approx \pi \left( 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right)
\] - Second Approximation:
This is more accurate and widely used:
\[
P \approx \pi (a + b) \left( 1 + \frac{3h}{10 + \sqrt{4 - 3h}} \right)
\]
where
\[
h = \left( \frac{a - b}{a + b} \right)^2
\]
Both formulas provide an efficient way to estimate the perimeter of an ellipse without resorting to elliptic integrals, which are more complex and computationally intensive.
Ramanujan's second approximation, in particular, strikes a balance between simplicity and accuracy, making it highly practical for many applications. It accounts for the shape of the ellipse more effectively by introducing the variable \( h \), which captures the relative difference between the semimajor and semiminor axes.
These approximations are particularly useful in various fields such as engineering, astronomy, and computer graphics, where quick and reasonably accurate calculations of elliptical perimeters are often required.
Using Numerical Integration
Numerical integration is a powerful method to estimate the perimeter of an oval, particularly when analytical solutions are difficult to obtain. Several numerical methods can be employed for this purpose, including the trapezoidal rule, Simpson's rule, and more sophisticated techniques involving elliptic integrals. Below, we detail these methods.
Trapezoidal Rule
The trapezoidal rule approximates the integral by dividing the interval into small segments, approximating the function as a straight line over each segment.
- Divide the interval \([a, b]\) into \(n\) subintervals of equal length \(\Delta x = \frac{b - a}{n}\).
- Evaluate the function at the endpoints of each subinterval.
- Sum the areas of the trapezoids formed by these evaluations.
The formula for the trapezoidal rule is:
\[
T_n = \frac{\Delta x}{2} \left( f(x_0) + 2 \sum_{i=1}^{n-1} f(x_i) + f(x_n) \right)
\]
Simpson's Rule
Simpson's rule provides a more accurate approximation by fitting parabolas to the subintervals.
- Divide the interval \([a, b]\) into \(n\) subintervals, where \(n\) is an even number.
- Calculate \(\Delta x = \frac{b - a}{n}\).
- Evaluate the function at the endpoints and midpoints of the subintervals.
- Apply the Simpson's rule formula to approximate the integral.
The formula for Simpson's rule is:
\[
S_n = \frac{\Delta x}{3} \left( f(x_0) + 4 \sum_{i \text{ odd}} f(x_i) + 2 \sum_{i \text{ even}} f(x_i) + f(x_n) \right)
\]
This method is particularly useful because it generally provides higher accuracy than the trapezoidal rule for the same number of subintervals.
Implementing Numerical Integration
To compute the perimeter of an oval using numerical integration, follow these steps:
- Define the function representing the ellipse's perimeter formula.
- Choose the numerical integration method (e.g., trapezoidal rule or Simpson's rule).
- Implement the chosen method in a computational tool (such as Python).
For example, using Python and the Simpson's rule:
from scipy.integrate import simps
import numpy as np
# Define the function for the ellipse
def ellipse_perimeter(a, b, theta):
return np.sqrt(a**2 * np.sin(theta)**2 + b**2 * np.cos(theta)**2)
# Parameters
a = 5 # semi-major axis
b = 3 # semi-minor axis
theta = np.linspace(0, 2 * np.pi, 1000)
# Compute the perimeter using Simpson's rule
y = ellipse_perimeter(a, b, theta)
perimeter = simps(y, theta)
print(f"The estimated perimeter of the ellipse is {perimeter:.2f}")
This script defines the ellipse's perimeter function, generates theta values over one full period, and uses Simpson's rule to integrate and estimate the perimeter.
Conclusion
Numerical integration methods provide robust techniques for approximating the perimeter of ovals and ellipses. By applying these methods, we can achieve accurate results even when analytical solutions are not feasible.
Series Expansion Methods
Series expansion methods provide an efficient way to approximate the perimeter of an ellipse. These methods involve expressing the perimeter as an infinite series and then truncating it to obtain a practical approximation. One of the most well-known series expansions is derived from the complete elliptic integral of the second kind.
For an ellipse with semi-major axis a and semi-minor axis b, and eccentricity e defined as \( e = \sqrt{1 - \left(\frac{b}{a}\right)^2} \), the perimeter P can be approximated by the series:
- The general form of the series expansion is: \[ P \approx 2\pi a \left(1 - \sum_{n=1}^{\infty} \frac{(2n-1)^2}{(2n)!^2} \left(\frac{e^2}{4}\right)^n \right) \]
- Truncating the series after a few terms, we get a more practical approximation: \[ P \approx 2\pi a \left(1 - \frac{1}{4}e^2 - \frac{3}{64}e^4 - \frac{5}{256}e^6 \right) \]
Another well-known approximation is provided by Ramanujan's series:
- Ramanujan's first approximation for the perimeter of an ellipse is: \[ P \approx \pi \left(3(a + b) - \sqrt{(3a + b)(a + 3b)}\right) \]
- A more accurate approximation by Ramanujan is: \[ P \approx \pi (a + b) \left(1 + \frac{3h}{10 + \sqrt{4 - 3h}}\right) \] where \( h = \left(\frac{a - b}{a + b}\right)^2 \).
These series expansion methods are particularly useful because they provide a balance between computational efficiency and accuracy. By choosing the number of terms to include in the series, one can control the trade-off between precision and computational effort.
Elliptic Integral Approach
The perimeter of an ellipse can be precisely calculated using elliptic integrals. This method involves advanced mathematical functions that provide exact results where elementary functions fall short.
An ellipse is defined by its semi-major axis \(a\) and semi-minor axis \(b\). The general equation for an ellipse is:
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
For an ellipse, the perimeter \(P\) can be given by the complete elliptic integral of the second kind \(E(k)\), where \(k\) is the elliptic modulus defined as:
\[ k = \sqrt{1 - \left(\frac{b}{a}\right)^2} \]
The perimeter is then expressed as:
\[ P = 4aE(k) \]
In practical terms, the elliptic integral \(E(k)\) is not straightforward to evaluate manually, and thus, computational tools are often employed. For example, using Python with the SciPy library, you can calculate it as:
import scipy.special
a = 10 # example value for semi-major axis
b = 5 # example value for semi-minor axis
eccentricity_squared = 1 - (b**2 / a**2)
perimeter = 4 * a * scipy.special.ellipe(eccentricity_squared)
print(perimeter)
Similarly, in Mathematica, the perimeter calculation would be:
4 * a * EllipticE[1 - b^2 / a^2]
This approach is particularly useful for high precision requirements, as it provides an exact result rather than an approximation. The elliptic integral method is a robust solution for determining the perimeter of an ellipse in various scientific and engineering applications.
Comparison of Different Methods
There are several methods to calculate the perimeter of an oval, or more specifically, an ellipse. Each method varies in complexity and accuracy. Here, we compare some of the commonly used approaches:
- Approximation Formulas:
- Ramanujan's First Approximation: \( P \approx \pi [3(a + b) - \sqrt{(3a + b)(a + 3b)}] \)
- Ramanujan's Second Approximation: \( P \approx \pi [a + b]\left(1 + \frac{3h}{10 + \sqrt{4 - 3h}}\right) \) where \( h = \frac{(a - b)^2}{(a + b)^2} \)
- Naive Formula: \( P \approx \pi (a + b) \)
- Numerical Integration:
- This method involves using numerical techniques to approximate the integral of the ellipse's circumference. It's more accurate for ellipses with high eccentricity but requires computational tools.
- Series Expansion Methods:
- These methods expand the perimeter into an infinite series, providing very accurate results for specific cases but can be complex and involve lengthy calculations.
- Elliptic Integral Approach:
- The exact perimeter \( P \) of an ellipse can be expressed using the complete elliptic integral of the second kind \( E(k) \): \[ P = 4aE(e) \] where \( e = \sqrt{1 - \frac{b^2}{a^2}} \) is the eccentricity and \( E(e) \) is the complete elliptic integral of the second kind.
Here is a comparison of these methods in terms of their accuracy and ease of use:
| Method | Accuracy | Ease of Use |
|---|---|---|
| Ramanujan's Approximations | High | Moderate |
| Numerical Integration | Very High | Low (requires computational tools) |
| Series Expansion | Very High | Low (complex calculations) |
| Elliptic Integral | Exact | Low (requires special functions) |
In conclusion, the choice of method depends on the required accuracy and the computational resources available. For practical purposes, Ramanujan's approximations provide a good balance between accuracy and simplicity. However, for precise scientific calculations, numerical integration or the elliptic integral approach is preferred.
Applications of Perimeter Calculations
The calculation of the perimeter of an oval (or ellipse) has a wide range of applications in various fields. Understanding these applications helps in appreciating the practical importance of mathematical concepts and their real-world implications.
- Engineering and Design:
In engineering and design, precise calculations of the perimeter of ovals are crucial for creating components that fit together seamlessly. For instance, in automotive design, the perimeter of elliptical gears and seals must be accurately calculated to ensure proper function and minimal wear.
- Astronomy:
Ovals and ellipses are fundamental in astronomy, particularly in the orbits of planets and satellites. Kepler's laws describe the elliptical orbits of celestial bodies, where the calculation of the perimeter helps in understanding orbital periods and distances.
- Architecture:
Architects often incorporate elliptical shapes in their designs for aesthetic and structural reasons. Calculating the perimeter of these shapes is important for determining material requirements and for precise construction.
- Medical Imaging:
In medical imaging, especially in the analysis of cross-sectional scans (such as MRI or CT scans), the shapes of organs or tumors are often approximated as ellipses. Calculating the perimeter helps in assessing sizes and growth rates accurately.
- Manufacturing:
In manufacturing, especially in industries involving cutting and shaping materials (like textiles, paper, or metal sheets), understanding the perimeter of ovals ensures efficient use of materials and reduces waste.
- Robotics:
Robotic motion planning often involves paths that can be elliptical. Calculating the perimeter of these paths is crucial for determining travel times and for programming efficient movement algorithms.
These are just a few examples demonstrating the diverse applications of perimeter calculations of ovals in various industries and scientific fields. The understanding and application of these calculations facilitate advancements and efficiencies in numerous areas.
Practical Examples and Exercises
Understanding the perimeter of an oval (ellipse) can be enhanced through practical examples and exercises. Below are a few examples and exercises to help solidify the concepts.
Example 1: Calculating the Perimeter of a Basic Ellipse
Given an ellipse with a semi-major axis \( a = 5 \) units and a semi-minor axis \( b = 3 \) units, use Ramanujan's approximation to find the perimeter.
Ramanujan's approximation formula:
\[ P \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right] \]
Substitute the given values:
\[ P \approx \pi \left[ 3(5 + 3) - \sqrt{(3 \cdot 5 + 3)(5 + 3 \cdot 3)} \right] \]
\[ P \approx \pi \left[ 3(8) - \sqrt{(15 + 3)(5 + 9)} \right] \]
\[ P \approx \pi \left[ 24 - \sqrt{18 \cdot 14} \right] \]
\[ P \approx \pi \left[ 24 - \sqrt{252} \right] \]
\[ P \approx \pi \left[ 24 - 15.87 \right] \]
\[ P \approx \pi \left[ 8.13 \right] \approx 25.54 \text{ units} \]
Example 2: Perimeter Calculation Using Numerical Integration
For a more accurate calculation, numerical integration can be used. Given the same ellipse with \( a = 5 \) units and \( b = 3 \) units, the perimeter \( P \) can be found using the integral:
\[ P = 4a \int_0^{\frac{\pi}{2}} \sqrt{1 - e^2 \sin^2 \theta} \, d\theta \]
where \( e = \sqrt{1 - \left(\frac{b}{a}\right)^2} \) is the eccentricity.
Substituting the values:
\[ e = \sqrt{1 - \left(\frac{3}{5}\right)^2} = \sqrt{1 - 0.36} = \sqrt{0.64} = 0.8 \]
Thus, the integral becomes:
\[ P = 20 \int_0^{\frac{\pi}{2}} \sqrt{1 - 0.64 \sin^2 \theta} \, d\theta \]
This integral can be evaluated using numerical methods or appropriate software for a precise result.
Exercise 1: Calculate the Perimeter Using Ramanujan's Approximation
- Given an ellipse with \( a = 6 \) units and \( b = 4 \) units, use Ramanujan's approximation to find the perimeter.
Exercise 2: Numerical Integration Practice
- Given an ellipse with \( a = 7 \) units and \( b = 5 \) units, set up the integral for the perimeter and solve it using numerical methods.
Example 3: Series Expansion Method
The perimeter of an ellipse can also be approximated using a series expansion. For small eccentricities, the series is:
\[ P \approx 2 \pi a \left( 1 - \frac{1}{4} e^2 - \frac{3}{64} e^4 - \frac{5}{256} e^6 - \cdots \right) \]
Given \( a = 4 \) units and \( b = 3 \) units, find the eccentricity \( e \) and calculate the perimeter using the first three terms of the series.
Steps:
- Calculate the eccentricity: \( e = \sqrt{1 - \left(\frac{b}{a}\right)^2} \)
- Substitute \( e \) into the series expansion.
- Sum the first three terms to approximate the perimeter.
Exercise 3: Series Expansion Practice
- Given an ellipse with \( a = 8 \) units and \( b = 6 \) units, calculate the perimeter using the series expansion method up to the second term.
Conclusion
These practical examples and exercises provide a comprehensive understanding of different methods to calculate the perimeter of an oval (ellipse). By practicing these problems, you will gain a deeper insight into the geometric and mathematical properties of ellipses.
Conclusion and Further Reading
Calculating the perimeter of an oval, particularly an ellipse, presents unique challenges due to the complex nature of its geometry. While the circumference of a circle is straightforward to determine, the perimeter of an ellipse requires more advanced mathematical techniques and approximations.
There are several methods to approximate the perimeter of an ellipse, including Ramanujan's approximations, numerical integration, series expansion, and elliptic integrals. Each method offers a different balance between simplicity and accuracy, making it important to choose the appropriate method based on the specific requirements of the problem at hand.
For further exploration and deeper understanding, consider the following resources:
- - A user-friendly introduction to various approximation methods.
- - Detailed explanations and solved examples.
- - Comprehensive coverage of the topic, including exact and approximate formulas.
- - An interactive tool for calculating the perimeter using various methods.
By exploring these resources, you can gain a more profound understanding of the mathematical intricacies involved in determining the perimeter of an oval and appreciate the rich history of mathematical discoveries in this field.
Hướng dẫn cách tính diện tích và chu vi của sân hình bầu dục để thu hút người xem và đảm bảo chính tả đúng.
Cách tính diện tích và chu vi của sân hình bầu dục
READ MORE:
Khám phá lý do tại sao không có phương trình cụ thể cho chu vi của elip và thu hút người xem bằng thông tin chính xác.
Tại sao không có phương trình cho chu vi của elip‽