Topic perimeter formula for a right triangle: Understanding the perimeter formula for a right triangle is essential for solving geometry problems efficiently. This article provides a comprehensive guide on calculating the perimeter using the formula, incorporating the Pythagorean theorem, and applying it in real-life scenarios. Enhance your mathematical skills with clear steps, examples, and practice problems tailored for learners at all levels.
Table of Content
- Perimeter Formula for a Right Triangle
- Introduction to Right Triangles
- Understanding Triangle Perimeters
- Basic Properties of Right Triangles
- Components of a Right Triangle
- Defining the Perimeter
- Perimeter Formula
- Using the Pythagorean Theorem
- Example Calculations
- Applications in Real Life
- Common Mistakes to Avoid
- Practice Problems
- Conclusion
- YOUTUBE: Tìm hiểu về diện tích và chu vi của tam giác vuông với Thầy J. Video này giúp bạn nắm vững các công thức quan trọng trong toán học.
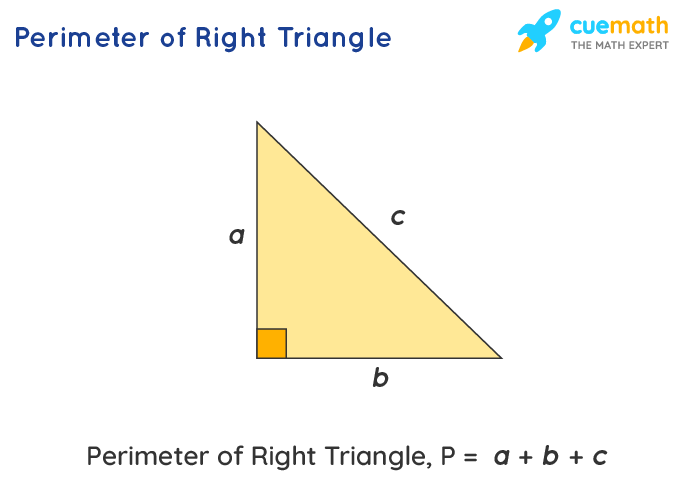
Perimeter Formula for a Right Triangle
The perimeter of a right triangle is the sum of the lengths of its three sides. In a right triangle, there are two legs (often denoted as a and b) and one hypotenuse (denoted as c). The hypotenuse is the side opposite the right angle and is the longest side of the triangle.
Formula
The formula to calculate the perimeter P of a right triangle is given by:
\[ P = a + b + c \]
Steps to Calculate the Perimeter
- Identify the lengths of the two legs of the right triangle (a and b).
- Use the Pythagorean theorem to find the length of the hypotenuse if not given: \[ c = \sqrt{a^2 + b^2} \]
- Add the lengths of the two legs and the hypotenuse to find the perimeter: \[ P = a + b + c \]
Example
Consider a right triangle with legs of lengths 3 units and 4 units.
- Calculate the hypotenuse using the Pythagorean theorem: \[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Calculate the perimeter: \[ P = 3 + 4 + 5 = 12 \]
Thus, the perimeter of the right triangle is 12 units.

READ MORE:
Introduction to Right Triangles
A right triangle is a type of triangle that has one angle measuring 90 degrees. This right angle creates a unique set of properties that distinguish right triangles from other triangles.
Key characteristics of right triangles include:
- Hypotenuse: The longest side of the triangle, opposite the right angle.
- Legs: The two sides that form the right angle.
The Pythagorean theorem is a fundamental principle related to right triangles. It states:
\( c^2 = a^2 + b^2 \)
where c is the length of the hypotenuse, and a and b are the lengths of the legs. This theorem is crucial for calculating the perimeter of a right triangle, as it allows you to determine the length of the hypotenuse when the lengths of the legs are known.
To summarize, right triangles are defined by their 90-degree angle, and their properties can be used to solve various geometric problems. Understanding these basics sets the stage for learning how to calculate the perimeter effectively.
Understanding Triangle Perimeters
The perimeter of a triangle is the total distance around the triangle, which is the sum of the lengths of its sides. For any triangle, including right triangles, the perimeter is calculated by adding the lengths of all three sides.
To understand how to calculate the perimeter of a right triangle, it is important to first recognize its components:
- Hypotenuse (c): The side opposite the right angle and the longest side of the triangle.
- Legs (a and b): The two sides that form the right angle.
The formula for the perimeter (P) of a right triangle is:
\[ P = a + b + c \]
Here is a step-by-step method to calculate the perimeter of a right triangle:
- Measure or determine the lengths of the two legs (a and b) and the hypotenuse (c) of the right triangle.
- Use the Pythagorean theorem if the length of the hypotenuse is not given: \[ c = \sqrt{a^2 + b^2} \]
- Sum the lengths of all three sides to find the perimeter: \[ P = a + b + c \]
To illustrate this, consider a right triangle with legs of lengths 3 units and 4 units:
- Using the Pythagorean theorem: \[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Then, calculate the perimeter: \[ P = 3 + 4 + 5 = 12 \]
Therefore, the perimeter of this right triangle is 12 units.
Basic Properties of Right Triangles
A right triangle, also known as a right-angled triangle, is a type of triangle that has one angle measuring 90 degrees. This unique property defines several important characteristics of right triangles:
- Right Angle: One of the angles in a right triangle is always 90 degrees.
- Hypotenuse: The side opposite the right angle is the longest side of the triangle and is called the hypotenuse.
- Legs: The other two sides of the triangle, which form the right angle, are called the legs. These are usually referred to as the adjacent and opposite sides, depending on the angle of interest.
The basic properties of right triangles can be summarized as follows:
- Pythagorean Theorem: The square of the hypotenuse (c) is equal to the sum of the squares of the legs (a and b). This can be written as:
\[
c^2 = a^2 + b^2
\] - Trigonometric Ratios: Right triangles are fundamental in trigonometry. The primary trigonometric ratios are defined based on the angles and sides of a right triangle:
- Sine: \(\sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{a}{c}\)
- Cosine: \(\cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{b}{c}\)
- Tangent: \(\tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} = \frac{a}{b}\)
- Angle Sum Property: The sum of all internal angles in any triangle is always 180 degrees. For a right triangle, this means:
where \(\alpha\) and \(\beta\) are the other two angles in the triangle.
\[
90^\circ + \alpha + \beta = 180^\circ
\]
These properties are essential for understanding the geometry and trigonometry of right triangles, as well as for solving various mathematical problems involving these triangles.
Components of a Right Triangle
A right triangle is defined by several key components that determine its shape and properties. These components include:
- Vertices: A right triangle has three vertices, which are the points where the sides meet. These are typically labeled as A, B, and C.
- Angles:
- Right Angle: One of the angles is exactly 90 degrees. This is the defining characteristic of a right triangle and is usually denoted by \(\angle C\).
- Acute Angles: The other two angles in the triangle are acute angles (less than 90 degrees). These angles add up to 90 degrees.
- Sides: The sides of a right triangle have specific names and properties:
- Hypotenuse: The side opposite the right angle is called the hypotenuse. It is the longest side of the triangle and is usually denoted by \(c\).
- Legs: The other two sides are called the legs. They form the right angle and are typically labeled as \(a\) and \(b\).
- Adjacent Side: The leg that forms one of the acute angles along with the hypotenuse.
- Opposite Side: The leg that is opposite to the acute angle being considered.
The relationships between these components can be summarized using the Pythagorean Theorem:
\[
c^2 = a^2 + b^2
\]
Additionally, the perimeter of a right triangle is the sum of the lengths of its three sides:
\[
\text{Perimeter} = a + b + c
\]
Understanding these components is essential for solving various problems related to right triangles, including calculating their area, perimeter, and understanding their geometric properties.
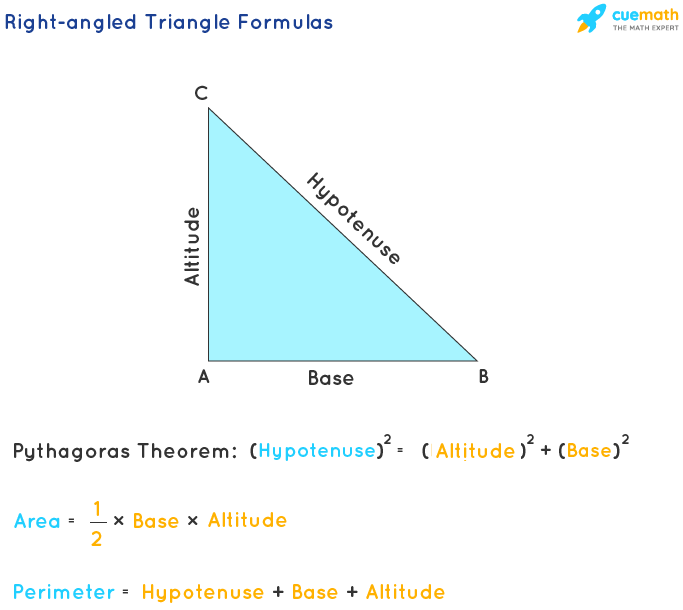
Defining the Perimeter
The perimeter of a right triangle is the total distance around the triangle. It is calculated by adding the lengths of all three sides. In a right triangle, these sides are the two legs (denoted as \(a\) and \(b\)) and the hypotenuse (denoted as \(c\)).
To define the perimeter mathematically, we use the formula:
\[
\text{Perimeter} = a + b + c
\]
Here’s a step-by-step explanation of how to calculate the perimeter of a right triangle:
- Identify the lengths of the legs: Measure or determine the lengths of the two legs of the triangle. These are the sides that form the right angle.
- Determine the length of the hypotenuse: If not already known, calculate the length of the hypotenuse using the Pythagorean Theorem:
\[
c = \sqrt{a^2 + b^2}
\] - Add the lengths of all three sides: Once you have the lengths of \(a\), \(b\), and \(c\), sum them up to find the perimeter:
\[
\text{Perimeter} = a + b + c
\]
Let's consider an example to illustrate the calculation:
- Suppose the lengths of the legs are \(a = 3\) units and \(b = 4\) units.
- First, calculate the hypotenuse using the Pythagorean Theorem:
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\] - Next, add the lengths of all sides to find the perimeter:
\[
\text{Perimeter} = 3 + 4 + 5 = 12 \text{ units}
\]
Therefore, the perimeter of the right triangle in this example is 12 units.
Understanding how to calculate the perimeter of a right triangle is fundamental in various applications, from geometry problems to real-world scenarios where precise measurements are crucial.
Perimeter Formula
The perimeter of a right triangle is the sum of the lengths of its three sides: the two legs and the hypotenuse. To derive the formula for the perimeter, we need to understand the components involved:
- Legs: These are the two sides that form the right angle, typically denoted as \(a\) and \(b\).
- Hypotenuse: This is the side opposite the right angle, denoted as \(c\). It can be calculated using the Pythagorean Theorem if not directly given.
The formula for the perimeter (\(P\)) of a right triangle is straightforward:
\[
P = a + b + c
\]
To better understand this formula, let's break it down step-by-step:
- Measure the Legs: Identify and measure the lengths of the legs \(a\) and \(b\).
- Calculate the Hypotenuse: If the hypotenuse \(c\) is not given, use the Pythagorean Theorem to find it:
\[
c = \sqrt{a^2 + b^2}
\] - Add the Side Lengths: Sum the lengths of the two legs and the hypotenuse to find the perimeter:
\[
P = a + b + c
\]
Consider the following example for clarity:
- Given: \(a = 5\) units, \(b = 12\) units
- Calculate Hypotenuse:
\[
c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \text{ units}
\] - Calculate Perimeter:
\[
P = 5 + 12 + 13 = 30 \text{ units}
\]
Therefore, the perimeter of the right triangle in this example is 30 units.
This formula is essential for solving various problems involving right triangles, including those in geometry, trigonometry, and real-world applications.
Using the Pythagorean Theorem
The Pythagorean Theorem is a fundamental principle in geometry, especially when dealing with right triangles. It states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This relationship is expressed as:
\( c^2 = a^2 + b^2 \)
where:
- \( c \) is the length of the hypotenuse
- \( a \) and \( b \) are the lengths of the other two sides
To use the Pythagorean Theorem to find the perimeter of a right triangle, follow these steps:
- Identify the lengths of the two legs (\( a \) and \( b \)) of the right triangle.
- Use the Pythagorean Theorem to calculate the length of the hypotenuse (\( c \)):
- Once you have the lengths of all three sides (\( a \), \( b \), and \( c \)), add them together to find the perimeter:
\( c = \sqrt{a^2 + b^2} \)
\( \text{Perimeter} = a + b + c \)
Here is an example:
- Suppose \( a = 3 \) units and \( b = 4 \) units.
- Calculate \( c \):
- Calculate the perimeter:
\( c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \) units
\( \text{Perimeter} = 3 + 4 + 5 = 12 \) units
By following these steps, you can easily find the perimeter of any right triangle using the Pythagorean Theorem.
Example Calculations
Let's look at some examples to understand how to calculate the perimeter of a right triangle.
Example 1
Find the perimeter of a right triangle with sides of length 6 cm, 8 cm, and 10 cm.
- Identify the sides:
- Side 1: \( a = 6 \) cm
- Side 2: \( b = 8 \) cm
- Hypotenuse: \( c = 10 \) cm
- Use the perimeter formula:
\[
P = a + b + c
\] - Substitute the values:
\[
P = 6 + 8 + 10 = 24 \text{ cm}
\]
The perimeter of the triangle is 24 cm.
Example 2
Calculate the perimeter of a right triangle with legs of 5 m and 12 m.
- Identify the sides:
- Leg 1: \( a = 5 \) m
- Leg 2: \( b = 12 \) m
- Find the hypotenuse using the Pythagorean theorem:
\[
c = \sqrt{a^2 + b^2} = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \text{ m}
\] - Use the perimeter formula:
\[
P = a + b + c
\] - Substitute the values:
\[
P = 5 + 12 + 13 = 30 \text{ m}
\]
The perimeter of the triangle is 30 m.
Example 3
Find the perimeter of a right triangle with one leg 7 inches and hypotenuse 25 inches.
- Identify the sides:
- Leg 1: \( a = 7 \) inches
- Hypotenuse: \( c = 25 \) inches
- Find the other leg using the Pythagorean theorem:
\[
b = \sqrt{c^2 - a^2} = \sqrt{25^2 - 7^2} = \sqrt{625 - 49} = \sqrt{576} = 24 \text{ inches}
\] - Use the perimeter formula:
\[
P = a + b + c
\] - Substitute the values:
\[
P = 7 + 24 + 25 = 56 \text{ inches}
\]
The perimeter of the triangle is 56 inches.
Example 4
Calculate the perimeter of a right triangle with legs 9 cm and 12 cm.
- Identify the sides:
- Leg 1: \( a = 9 \) cm
- Leg 2: \( b = 12 \) cm
- Find the hypotenuse using the Pythagorean theorem:
\[
c = \sqrt{a^2 + b^2} = \sqrt{9^2 + 12^2} = \sqrt{81 + 144} = \sqrt{225} = 15 \text{ cm}
\] - Use the perimeter formula:
\[
P = a + b + c
\] - Substitute the values:
\[
P = 9 + 12 + 15 = 36 \text{ cm}
\]
The perimeter of the triangle is 36 cm.
Applications in Real Life
Understanding the perimeter formula for a right triangle has numerous practical applications in everyday life. Here are some examples:
-
Construction
In building construction, the perimeter of triangular sections is often used to determine the amount of materials needed, such as framing for roofs. Ensuring precise measurements helps in creating stable and well-fitted structures.
-
Landscaping
Landscape architects use the perimeter of triangular plots to calculate the fencing or edging required for gardens and lawns. Accurate measurements ensure proper layout and efficient use of materials.
-
Navigation and Surveying
Surveyors and navigators apply the perimeter and properties of right triangles to measure distances and plot maps. This is essential in determining boundaries, land areas, and in the planning of roads and bridges.
-
Astronomy
In astronomy, right triangles help in calculating distances between celestial objects and understanding their positions. The perimeter helps in creating accurate models and simulations of astronomical phenomena.
-
Art and Design
Artists and designers use the principles of right triangles to create aesthetically pleasing compositions. Understanding the perimeter helps in planning and constructing various elements within a piece, ensuring balance and harmony.
-
Fashion
Fashion designers often use the perimeter of triangular patterns to create garments. This helps in determining fabric requirements and ensuring precise cuts and fittings for various designs.
-
Technology
In computer graphics and gaming, right triangles are fundamental in rendering scenes and models. The perimeter calculations assist in creating accurate and realistic representations of virtual environments.
Overall, the knowledge of the perimeter formula for a right triangle is invaluable across multiple fields, enabling professionals to solve practical problems efficiently and accurately.
Common Mistakes to Avoid
When calculating the perimeter of a right triangle, it's essential to be aware of common mistakes that can lead to incorrect results. Here are some typical errors and tips on how to avoid them:
-
Confusing Side Lengths
It's easy to mix up the lengths of the legs and the hypotenuse, especially in non-standard triangles.
- Tip: Clearly label each side of the triangle and double-check your labels before performing calculations.
-
Incorrect Application of the Pythagorean Theorem
Using the Pythagorean theorem incorrectly can result in wrong values for the hypotenuse or legs.
- Tip: Remember, the Pythagorean theorem \(a^2 + b^2 = c^2\) applies only to right triangles where \(c\) is the hypotenuse.
-
Arithmetic Errors
Simple arithmetic mistakes can lead to incorrect perimeter values.
- Tip: Perform each calculation step carefully, and consider using a calculator to ensure accuracy.
-
Ignoring Units of Measurement
Not converting all measurements to the same unit can cause significant errors.
- Tip: Always standardize units before starting calculations.
-
Misinterpreting Triangle Properties
Misunderstanding the properties of right triangles can lead to incorrect applications of formulas.
- Tip: Ensure you understand that the hypotenuse is the longest side and opposite the right angle in a right triangle.
-
Forgetting to Include All Sides in the Perimeter Calculation
When summing the sides, missing any side will give an incorrect perimeter.
- Tip: Verify that you have included all three sides in your final perimeter calculation.
By being mindful of these common mistakes, you can improve the accuracy of your perimeter calculations for right triangles. Approach each problem methodically, and always double-check your work to ensure correctness.
Practice Problems
Test your understanding of the perimeter formula for right triangles with these practice problems. Use the Pythagorean theorem and the perimeter formula to find the solutions. Try to solve each problem on your own before checking the answers.
-
A right triangle has sides of lengths 6 m, 8 m, and 10 m. What is the perimeter?
Solution:
- Given sides: \(a = 6 \, \text{m}\), \(b = 8 \, \text{m}\), \(c = 10 \, \text{m}\)
- Perimeter formula: \( p = a + b + c \)
- Calculate: \( p = 6 + 8 + 10 = 24 \, \text{m} \)
-
A right triangle has legs of lengths 5 cm and 12 cm. What is the perimeter?
Solution:
- Given legs: \(a = 5 \, \text{cm}\), \(b = 12 \, \text{cm}\)
- Find hypotenuse \(c\) using the Pythagorean theorem: \(c = \sqrt{a^2 + b^2}\)
- Calculate: \(c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \, \text{cm}\)
- Perimeter formula: \( p = a + b + c \)
- Calculate: \( p = 5 + 12 + 13 = 30 \, \text{cm} \)
-
What is the perimeter of a right triangle with sides of lengths 9 m and 12 m?
Solution:
- Given legs: \(a = 9 \, \text{m}\), \(b = 12 \, \text{m}\)
- Find hypotenuse \(c\) using the Pythagorean theorem: \(c = \sqrt{a^2 + b^2}\)
- Calculate: \(c = \sqrt{9^2 + 12^2} = \sqrt{81 + 144} = \sqrt{225} = 15 \, \text{m}\)
- Perimeter formula: \( p = a + b + c \)
- Calculate: \( p = 9 + 12 + 15 = 36 \, \text{m} \)
-
Find the perimeter of a right triangle with sides of length 7 cm, 24 cm, and 25 cm.
Solution:
- Given sides: \(a = 7 \, \text{cm}\), \(b = 24 \, \text{cm}\), \(c = 25 \, \text{cm}\)
- Perimeter formula: \( p = a + b + c \)
- Calculate: \( p = 7 + 24 + 25 = 56 \, \text{cm} \)
-
A right triangle has one leg of 8 m and a hypotenuse of 17 m. Find the perimeter.
Solution:
- Given leg: \(a = 8 \, \text{m}\), hypotenuse: \(c = 17 \, \text{m}\)
- Find the other leg \(b\) using the Pythagorean theorem: \(b = \sqrt{c^2 - a^2}\)
- Calculate: \(b = \sqrt{17^2 - 8^2} = \sqrt{289 - 64} = \sqrt{225} = 15 \, \text{m}\)
- Perimeter formula: \( p = a + b + c \)
- Calculate: \( p = 8 + 15 + 17 = 40 \, \text{m} \)
Conclusion
Understanding the perimeter formula for a right triangle is a fundamental aspect of geometry that not only helps in academic pursuits but also in practical applications. By mastering this concept, you gain the ability to solve real-world problems and develop a deeper appreciation for the mathematical principles that govern shapes and spaces.
The key takeaways from our discussion include:
- The perimeter of a right triangle is the sum of the lengths of its three sides.
- Using the Pythagorean Theorem, you can calculate the hypotenuse if only the lengths of the two legs are known.
- Practical applications of this knowledge range from construction and design to navigation and more.
- Common mistakes to avoid include incorrect calculations of side lengths and misunderstanding the application of the Pythagorean Theorem.
We encourage you to continue practicing with various problems and scenarios to solidify your understanding. The more you practice, the more intuitive these calculations will become. Geometry is not just about numbers and formulas; it is about understanding the space around us and how we interact with it.
Keep exploring, stay curious, and remember that every mathematical problem you solve enhances your ability to think critically and creatively. As you continue your journey in learning geometry, let each new challenge be an opportunity to grow and discover the fascinating world of mathematics.

Tìm hiểu về diện tích và chu vi của tam giác vuông với Thầy J. Video này giúp bạn nắm vững các công thức quan trọng trong toán học.
Diện Tích và Chu Vi của Tam Giác Vuông | Toán với Thầy J
READ MORE:
Hướng dẫn cách tìm diện tích và chu vi của tam giác vuông một cách chi tiết và dễ hiểu. Video này giúp bạn nắm vững các công thức quan trọng trong toán học.
Cách tìm Diện Tích và Chu Vi của Tam Giác Vuông