Topic perimeter formula of a rhombus: Discover the essentials of the rhombus and learn how to calculate its perimeter with our comprehensive guide. We cover everything from the basic definition and properties to detailed examples and common pitfalls, ensuring you master the perimeter formula of a rhombus with ease. Dive in for practical insights and handy tips!
Table of Content
- Perimeter Formula of a Rhombus
- Introduction to Rhombus
- Definition of a Rhombus
- Properties of a Rhombus
- Understanding Perimeter
- Perimeter Formula of a Rhombus
- Derivation of the Perimeter Formula
- Step-by-Step Calculation Examples
- Applications of the Perimeter Formula
- Common Mistakes to Avoid
- Practice Problems
- FAQs on Rhombus Perimeter
- Conclusion
- YOUTUBE: Hướng dẫn chi tiết cách tính diện tích và chu vi của hình thoi, giúp bạn nắm vững kiến thức một cách dễ dàng và hiệu quả.
Perimeter Formula of a Rhombus
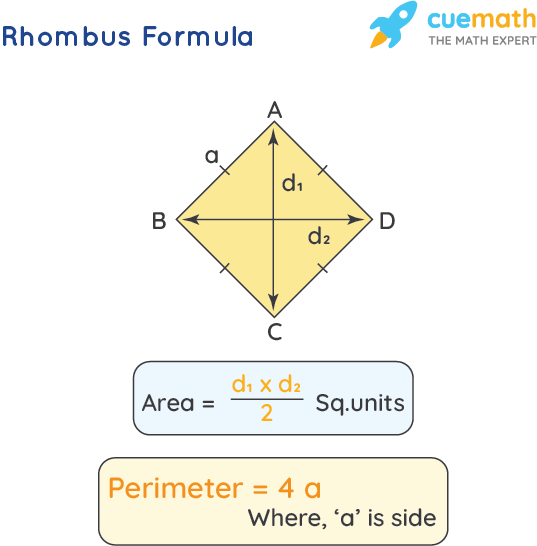
The perimeter of a rhombus can be calculated using the length of one of its sides. Since all sides of a rhombus are of equal length, the perimeter is simply four times the length of one side.
Formula
If \( a \) is the length of a side of the rhombus, then the perimeter \( P \) is given by:
\[
P = 4a
\]
Example Calculation
Suppose the length of a side of the rhombus is 5 units. The perimeter can be calculated as follows:
\[
P = 4 \times 5 = 20 \text{ units}
\]
Alternative Formula Using Diagonals
The perimeter of a rhombus can also be derived if the lengths of the diagonals are known. Let \( d_1 \) and \( d_2 \) be the lengths of the diagonals. The length of a side can be found using the Pythagorean theorem since the diagonals bisect each other at right angles:
\[
a = \sqrt{\left(\frac{d_1}{2}\right)^2 + \left(\frac{d_2}{2}\right)^2}
\]
Then, the perimeter can be calculated as:
\[
P = 4 \sqrt{\left(\frac{d_1}{2}\right)^2 + \left(\frac{d_2}{2}\right)^2}
\]
Example Calculation Using Diagonals
Suppose the lengths of the diagonals of the rhombus are 6 units and 8 units. The side length and perimeter can be calculated as follows:
\[
a = \sqrt{\left(\frac{6}{2}\right)^2 + \left(\frac{8}{2}\right)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ units}
\]
Therefore, the perimeter is:
\[
P = 4 \times 5 = 20 \text{ units}
\]
READ MORE:
Introduction to Rhombus
A rhombus is a type of quadrilateral that is both fascinating and unique. It is a four-sided polygon where all sides have equal length, making it a special case of a parallelogram. The defining characteristics of a rhombus include:
- All four sides are of equal length (\(a\)).
- Opposite angles are equal.
- The diagonals bisect each other at right angles and are not equal in length.
- The diagonals also bisect the angles of the rhombus.
In addition to these properties, the rhombus has intriguing geometric relationships. For example, if the diagonals are given as \(d_1\) and \(d_2\), they form right triangles with the sides of the rhombus. This leads to useful formulas for various calculations.
Understanding these properties is essential as they play a crucial role in calculating the perimeter and area of a rhombus. The perimeter of a rhombus is simply four times the length of one of its sides, given by the formula:
\( P = 4a \)
Whether you are studying for a math test or simply exploring geometric shapes, knowing the fundamental aspects of a rhombus will provide a solid foundation for deeper exploration. Continue reading to learn more about the perimeter formula of a rhombus and how to apply it in different scenarios.
Definition of a Rhombus
A rhombus is a distinctive and symmetrical quadrilateral, characterized by its equal-length sides. It can be seen as an equilateral parallelogram, showcasing both elegance and balance in geometry. To fully understand what a rhombus is, consider the following detailed attributes:
- Equilateral Sides: All four sides of a rhombus have equal lengths. If each side length is denoted as \( a \), then:
\( AB = BC = CD = DA = a \)
- Opposite Angles: The opposite angles of a rhombus are equal. For instance, if \( \angle A = \angle C \) and \( \angle B = \angle D \), these angles are congruent:
\( \angle A = \angle C \) and \( \angle B = \angle D \)
- Diagonals: The diagonals of a rhombus intersect at right angles (90 degrees) and bisect each other. This means that each diagonal divides the rhombus into two congruent right triangles. If \( d_1 \) and \( d_2 \) are the lengths of the diagonals, then:
\( AC = d_1 \) and \( BD = d_2 \)
- Angle Bisectors: The diagonals not only intersect at right angles but also bisect the internal angles of the rhombus. This property is crucial for understanding the internal symmetry of the shape.
The unique combination of these properties makes the rhombus a fascinating figure in geometry. It can also be considered a special type of kite and parallelogram, which highlights its versatility and geometric richness.
Understanding the definition and characteristics of a rhombus is fundamental in grasping its perimeter and area calculations. The perimeter, which is the total length around the shape, is straightforwardly given by the formula:
\( P = 4a \)
This formula reflects the simplicity of the rhombus’s perimeter calculation, directly tied to its defining equal side lengths. Continue reading to explore how these properties relate to practical applications and further geometric insights.
Properties of a Rhombus
A rhombus is a type of polygon that falls under the category of quadrilaterals. It has several unique properties that distinguish it from other quadrilaterals. Here are the key properties of a rhombus:
- All sides are equal: Each side of a rhombus has the same length.
- Opposite angles are equal: The opposite angles of a rhombus are congruent.
- Adjacent angles are supplementary: Any two adjacent angles in a rhombus add up to 180 degrees.
- Diagonals bisect each other: The diagonals of a rhombus intersect at right angles (90 degrees) and bisect each other.
- Diagonals bisect angles: Each diagonal of a rhombus bisects the angles from which it is drawn.
- Symmetry: A rhombus has two lines of symmetry along its diagonals.
The properties of a rhombus can be summarized in the following table:
| Property | Description |
| Equal Sides | All four sides of a rhombus are of equal length. |
| Equal Opposite Angles | The opposite angles in a rhombus are equal. |
| Supplementary Adjacent Angles | Any two adjacent angles add up to 180 degrees. |
| Diagonals Bisect Each Other | The diagonals intersect at right angles and bisect each other. |
| Diagonals Bisect Angles | Each diagonal bisects the angles from which it is drawn. |
| Symmetry | A rhombus has two lines of symmetry along its diagonals. |
Understanding Perimeter
The perimeter of a geometric shape is the total distance around the shape's boundary. For polygons, this means summing the lengths of all sides. In simpler terms, if you walked around the shape, the perimeter would be the total distance you covered.
For a rhombus, which is a type of polygon with four equal sides, understanding its perimeter involves a few key points:
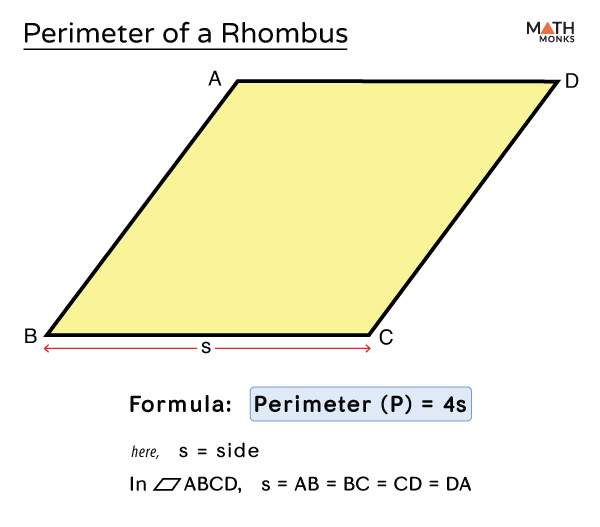
- A rhombus is a quadrilateral with all sides of equal length.
- The diagonals of a rhombus bisect each other at right angles.
- The diagonals are not equal but they bisect each other perpendicularly.
To calculate the perimeter of a rhombus, you can use the following formulae depending on the information you have:
- When the side length (\(s\)) is known:
- Formula: \( P = 4s \)
- Example: If the side length of a rhombus is 8 units, the perimeter would be \( P = 4 \times 8 = 32 \) units.
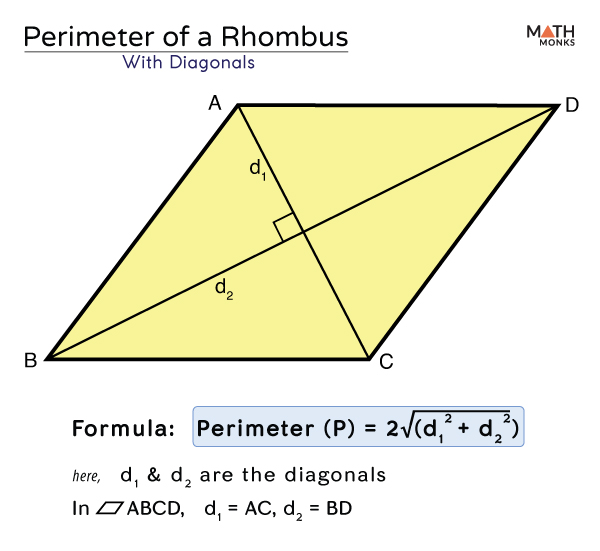
- When the lengths of the diagonals (\(d_1\) and \(d_2\)) are known:
- Formula: \( P = 2 \sqrt{d_1^2 + d_2^2} \)
- Example: If the diagonals of a rhombus are 6 units and 8 units, the perimeter would be \( P = 2 \sqrt{6^2 + 8^2} = 2 \sqrt{36 + 64} = 2 \sqrt{100} = 20 \) units.
Understanding these formulas is crucial for accurately calculating the perimeter of a rhombus, whether you know the side length or the lengths of the diagonals. This knowledge is not only fundamental for geometry studies but also practical in various real-world applications where the perimeter of rhombus-shaped objects needs to be determined.
Perimeter Formula of a Rhombus
The perimeter of a rhombus is the total distance around the shape. Since all four sides of a rhombus are equal in length, the perimeter can be calculated easily if the length of one side is known.
The formula to find the perimeter \( P \) of a rhombus is:
\[
P = 4 \times a
\]
where \( a \) is the length of one side of the rhombus.
To understand this formula, follow these steps:
- Measure the length of one side of the rhombus. Let's denote this length as \( a \).
- Multiply the length \( a \) by 4 because a rhombus has four equal sides.
For example, if the length of one side of the rhombus is 5 units, the perimeter is calculated as follows:
\[
P = 4 \times 5 = 20 \text{ units}
\]
This formula is derived from the property of the rhombus that all four sides are of equal length.
In summary, the perimeter formula for a rhombus is straightforward and relies on the knowledge that each side of the rhombus is the same length.
Derivation of the Perimeter Formula
The perimeter of a rhombus is the total distance around its four sides. Since all sides of a rhombus are of equal length, the formula for the perimeter is quite straightforward.
Using Side Length
If the length of one side of the rhombus is known, the perimeter (P) can be calculated by multiplying the side length (a) by 4:
For example, if the side length of a rhombus is 5 units, the perimeter is:
Using Diagonals
If the lengths of the diagonals are known, the perimeter can be derived using the Pythagorean theorem. Consider a rhombus with diagonals d1 and d2. Each diagonal bisects the rhombus into four right triangles.
The half-lengths of the diagonals are:
Using the Pythagorean theorem in one of these right triangles, we find the side length a:
The perimeter is then:
For example, if d1 = 6 units and d2 = 8 units, the perimeter is:
Thus, by knowing either the side length or the diagonals, you can easily derive the perimeter of a rhombus.
Step-by-Step Calculation Examples
In this section, we'll go through detailed examples to help you understand how to calculate the perimeter of a rhombus using different given parameters.
Example 1: Using Side Length
- Assume the length of one side (a) of the rhombus is 8 cm.
- Apply the perimeter formula: \( P = 4 \times a \).
- Calculate the perimeter: \( P = 4 \times 8 \, \text{cm} = 32 \, \text{cm} \).
Example 2: Using Diagonals
In cases where only the lengths of the diagonals are known, you can still find the perimeter by first determining the side length using the Pythagorean theorem.
- Given diagonal lengths are \( d_1 = 12 \, \text{cm} \) and \( d_2 = 9 \, \text{cm} \).
- Calculate the half lengths of the diagonals: \( \frac{d_1}{2} = 6 \, \text{cm} \) and \( \frac{d_2}{2} = 4.5 \, \text{cm} \).
- Apply the Pythagorean theorem to find one side length: \[ a = \sqrt{\left(\frac{d_1}{2}\right)^2 + \left(\frac{d_2}{2}\right)^2} = \sqrt{6^2 + 4.5^2} = \sqrt{36 + 20.25} = \sqrt{56.25} \approx 7.5 \, \text{cm} \]
- Calculate the perimeter: \( P = 4 \times 7.5 \, \text{cm} \approx 30 \, \text{cm} \).
Example 3: Using Perimeter and Finding Missing Side
- Given the perimeter of a rhombus is 60 cm.
- Use the perimeter formula to find the side length: \[ a = \frac{P}{4} = \frac{60 \, \text{cm}}{4} = 15 \, \text{cm} \]
Example 4: Practical Application
Let's say we need to find the length of fencing required to enclose a rhombus-shaped garden plot.
- Each side of the rhombus is 10 meters.
- Apply the perimeter formula: \( P = 4 \times a = 4 \times 10 \, \text{m} = 40 \, \text{m} \).
Hence, 40 meters of fencing is required to enclose the garden.
Applications of the Perimeter Formula
The perimeter formula of a rhombus, given by \( P = 4s \) where \( s \) is the side length, has various practical applications across different fields. Here are some notable applications:
- Architecture and Construction:
In the design and construction of buildings, especially in tiling and flooring, knowing the perimeter of rhombus-shaped tiles is essential. It helps in calculating the required materials and ensuring precise fitting.
- Landscaping:
For garden designs that incorporate rhombus-shaped plots or pathways, the perimeter formula is used to determine the boundary length, assisting in the planning and allocation of plants or decorative elements.
- Art and Design:
Artists and designers often use geometric shapes, including rhombuses, in their work. Calculating the perimeter allows for accurate framing, border designs, and the creation of aesthetically pleasing patterns.
- Manufacturing:
In manufacturing processes, particularly in metalworking and sheet cutting, understanding the perimeter of rhombus-shaped components ensures precise cutting, reducing material waste and optimizing production efficiency.
- Sports Fields:
Some sports fields and tracks may incorporate rhombus-shaped areas. Knowing the perimeter helps in the design and maintenance of these spaces, ensuring they meet regulatory standards and provide the necessary play area.
- Educational Tools:
Teachers use rhombus shapes in geometry lessons to explain concepts of symmetry, perimeter, and area. Understanding the perimeter formula enhances students' grasp of fundamental mathematical principles.
- Urban Planning:
Urban planners may use rhombus-shaped plots for parks, intersections, or buildings. Calculating the perimeter is crucial for planning the infrastructure and ensuring efficient use of space.
Overall, the perimeter formula of a rhombus is a versatile tool with significant applications in various domains, highlighting the importance of geometric principles in practical scenarios.

Common Mistakes to Avoid
When calculating the perimeter of a rhombus, there are several common mistakes that students and professionals should avoid to ensure accuracy. Here are some of the key mistakes to watch out for:
- Incorrect Formula Usage:
Ensure that you use the correct formula for the given information. The perimeter of a rhombus with side length \( s \) is given by \( P = 4s \). If using diagonals \( d_1 \) and \( d_2 \), the formula is \( P = 2\sqrt{d_1^2 + d_2^2} \).
- Misidentifying the Shape:
A rhombus is often confused with other quadrilaterals such as squares and parallelograms. Remember, all four sides of a rhombus are of equal length, but it does not necessarily have right angles like a square.
- Incorrect Diagonal Calculations:
When using the diagonal formula, ensure that you correctly square the lengths of the diagonals and add them before taking the square root. Double-check the diagonal values to avoid errors.
- Misinterpreting Units:
Always use consistent units throughout the calculation. If the side lengths are given in different units, convert them to the same unit before applying the formula.
- Rounding Errors:
Be mindful of rounding errors, especially when dealing with square roots. Carry out the calculations to a sufficient number of decimal places and round off the final result as needed.
- Assuming Equal Diagonals:
Do not assume that the diagonals of a rhombus are equal. The diagonals of a rhombus bisect each other at right angles, but they are not necessarily of equal length.
- Ignoring Special Cases:
In problems where additional properties or constraints are given, such as specific angles or relationships between sides and diagonals, ensure that these are taken into account in your calculations.
By being aware of these common mistakes, you can improve your accuracy when calculating the perimeter of a rhombus and ensure that your results are reliable.
Practice Problems
Here are some practice problems to help you understand and apply the perimeter formula of a rhombus:
-
A rhombus has sides of length 6 cm. Calculate the perimeter.
Solution:
- Use the formula: \( P = 4s \)
- \( P = 4 \times 6 \)
- \( P = 24 \) cm
-
The perimeter of a rhombus is 64 meters. Find the length of one side.
Solution:
- Use the formula: \( P = 4s \)
- \( 64 = 4s \)
- Solve for \( s \): \( s = \frac{64}{4} \)
- \( s = 16 \) meters
-
A rhombus has a side length of 9 inches. Determine its perimeter.
Solution:
- Use the formula: \( P = 4s \)
- \( P = 4 \times 9 \)
- \( P = 36 \) inches
-
If a rhombus has a perimeter of 100 cm, what is the length of each side?
Solution:
- Use the formula: \( P = 4s \)
- \( 100 = 4s \)
- Solve for \( s \): \( s = \frac{100}{4} \)
- \( s = 25 \) cm
-
The side of a rhombus is 5.5 feet. Calculate its perimeter.
Solution:
- Use the formula: \( P = 4s \)
- \( P = 4 \times 5.5 \)
- \( P = 22 \) feet
FAQs on Rhombus Perimeter
Here are some frequently asked questions about the perimeter of a rhombus:
1. What is the formula for the perimeter of a rhombus?
The formula for the perimeter of a rhombus is given by:
\[ P = 4s \]
where \( P \) is the perimeter and \( s \) is the length of one side of the rhombus.
2. How do you find the perimeter if only the diagonals are given?
If you are given the lengths of the diagonals, you can find the side length using the Pythagorean theorem. If \( d_1 \) and \( d_2 \) are the lengths of the diagonals, then the side length \( s \) can be found as:
\[ s = \sqrt{\left(\frac{d_1}{2}\right)^2 + \left(\frac{d_2}{2}\right)^2} \]
Once you have the side length, you can use the perimeter formula \( P = 4s \).
3. Can a square be considered a rhombus?
Yes, a square is a special type of rhombus where all interior angles are equal to 90 degrees. Therefore, the perimeter formula for a square is the same as that for a rhombus.
4. How is the perimeter of a rhombus related to its side length?
The perimeter of a rhombus is directly proportional to its side length. If the side length of a rhombus doubles, its perimeter also doubles. This is because the perimeter formula \( P = 4s \) simply multiplies the side length by 4.
5. Why is understanding the perimeter of a rhombus important?
Knowing how to calculate the perimeter of a rhombus is useful in various real-life applications, such as determining the amount of material needed for construction projects, designing objects, and solving geometric problems in mathematics.
6. Are the diagonals of a rhombus equal?
No, the diagonals of a rhombus are not equal. However, they bisect each other at right angles (90 degrees) and each diagonal splits the rhombus into two congruent triangles.
7. How can you verify if a given quadrilateral is a rhombus?
To verify if a given quadrilateral is a rhombus, check the following properties:
- All four sides are of equal length.
- Opposite angles are equal.
- Diagonals bisect each other at right angles.
Conclusion
Understanding the perimeter of a rhombus is essential in various mathematical and practical applications. The formula for the perimeter, which is given by
In this guide, we have explored the definition and properties of a rhombus, the detailed derivation of the perimeter formula, and step-by-step examples to ensure thorough comprehension. Additionally, we've discussed the real-life applications of this formula, highlighting its relevance in fields like architecture and design.
Common mistakes such as confusing the formula with that of other quadrilaterals or misapplying the diagonal lengths have been addressed, ensuring clarity and accuracy in calculations. Practice problems and FAQs have further reinforced the understanding of the concept.
By mastering the perimeter formula of a rhombus, students and professionals alike can enhance their mathematical skills and apply this knowledge effectively in academic and real-world scenarios. Keep practicing and exploring more geometric properties to build a robust foundation in mathematics.
Hướng dẫn chi tiết cách tính diện tích và chu vi của hình thoi, giúp bạn nắm vững kiến thức một cách dễ dàng và hiệu quả.
Cách tìm Diện tích và Chu vi của Hình thoi
READ MORE:
Hướng dẫn chi tiết cách tính chu vi của hình thoi từ các đường chéo, giúp bạn nắm vững kiến thức hình học một cách dễ dàng.
Tìm Chu vi của Hình thoi từ Đường chéo | Hình học
