Topic formula for finding perimeter of a circle: Discover the formula for finding the perimeter of a circle with this comprehensive guide. We'll break down the steps and provide clear examples to help you understand and apply the circumference formula using both radius and diameter. Perfect for students, teachers, and anyone looking to deepen their math knowledge.
Table of Content
- Formula for Finding the Perimeter of a Circle
- Introduction to Perimeter of a Circle
- Understanding the Concept of Circumference
- Basic Formulas for Calculating Circumference
- Components and Variables Explained
- Deriving the Formulas
- Practical Examples and Problem Solving
- Visual Representations
- Applications in Real Life
- FAQs and Common Misconceptions
- Advanced Topics Related to Circle Perimeter
- Conclusion and Summary
- YOUTUBE:
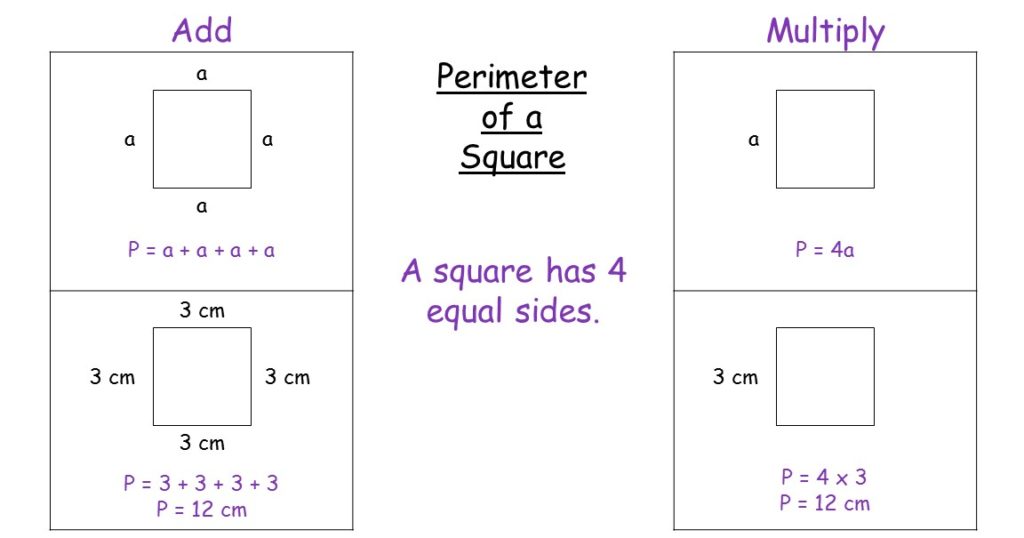
Formula for Finding the Perimeter of a Circle
The perimeter of a circle is commonly referred to as the circumference. The formula to find the circumference (C) is derived from the circle's radius (r) or diameter (d). Below, we explore these formulas and provide detailed examples for better understanding.
Basic Formulas
- When the radius is known:
\[ C = 2 \pi r \]
- When the diameter is known:
\[ C = \pi d \]
Components of the Formula
| Variable | Description |
| \( C \) | The circumference or perimeter of the circle |
| \( r \) | The radius of the circle (distance from the center to any point on the circle) |
| \( d \) | The diameter of the circle (distance across the circle, through the center), which is twice the radius \( (d = 2r) \) |
| \( \pi \) | Pi, a constant approximately equal to 3.14159 |
Examples
- Finding the circumference using the radius:
If the radius of a circle is 7 units, the circumference can be calculated as:
\[ C = 2 \pi \times 7 = 14 \pi \approx 43.98 \, \text{units} \]
- Finding the circumference using the diameter:
If the diameter of a circle is 10 units, the circumference can be calculated as:
\[ C = \pi \times 10 = 10 \pi \approx 31.42 \, \text{units} \]
Visual Representation
Below is a simple diagram showing a circle with its radius and diameter:
Additional Information
The concept of circumference is fundamental in geometry and is used in various applications in science, engineering, and everyday life. Understanding how to calculate it is crucial for solving problems involving circles.

READ MORE:
Introduction to Perimeter of a Circle
The perimeter of a circle, also known as the circumference, is the distance around the circle. It is a fundamental concept in geometry and is crucial for various applications in mathematics and real life.
To understand how to calculate the perimeter of a circle, you need to be familiar with two important terms:
- Radius (r): The distance from the center of the circle to any point on its edge.
- Diameter (d): The distance across the circle, passing through the center. It is twice the radius, so \( d = 2r \).
The formula for finding the perimeter (circumference) of a circle can be expressed in two ways:
- Using the radius: \( C = 2\pi r \)
- Using the diameter: \( C = \pi d \)
Where \( \pi \) (pi) is a constant approximately equal to 3.14159. This constant represents the ratio of the circumference of any circle to its diameter.
Let's look at these formulas step by step:
- Measure the radius or diameter of the circle.
- If you have the radius, multiply it by 2 to get the diameter, or use it directly in the formula \( C = 2\pi r \).
- If you have the diameter, use the formula \( C = \pi d \).
- Multiply the radius or diameter by \( \pi \) to find the circumference.
For example, if a circle has a radius of 5 units:
- Using the radius formula: \( C = 2\pi \times 5 = 10\pi \approx 31.4159 \) units
- Using the diameter formula: First find the diameter \( d = 2 \times 5 = 10 \) units, then \( C = \pi \times 10 = 10\pi \approx 31.4159 \) units
Understanding these basic formulas and steps will help you easily find the perimeter of any circle.
Understanding the Concept of Circumference
The circumference of a circle is the linear distance around its edge. It is an essential concept in geometry, representing the boundary length of a circle.
To understand circumference, let's break it down into key components:
- Circle: A shape with all points equidistant from a central point.
- Radius (r): The distance from the center of the circle to any point on its circumference.
- Diameter (d): The distance across the circle, passing through the center, equal to twice the radius (\(d = 2r\)).
- Pi (\( \pi \)): A mathematical constant approximately equal to 3.14159, representing the ratio of a circle's circumference to its diameter.
The formula to calculate the circumference (C) of a circle can be expressed in two ways:
- Using the radius: \( C = 2\pi r \)
- Using the diameter: \( C = \pi d \)
Here’s a step-by-step explanation:
- Measure the radius or diameter of the circle.
- For the radius, use the formula \( C = 2\pi r \):
- Multiply the radius (r) by 2 to get the diameter (d).
- Multiply the result by \( \pi \) to get the circumference.
- For the diameter, use the formula \( C = \pi d \):
- Simply multiply the diameter (d) by \( \pi \) to get the circumference.
Let’s look at an example:
| Given: | Radius (r) = 7 units |
| Using \( C = 2\pi r \): | \( C = 2 \times \pi \times 7 = 14\pi \approx 43.9823 \) units |
| Given: | Diameter (d) = 14 units |
| Using \( C = \pi d \): | \( C = \pi \times 14 = 14\pi \approx 43.9823 \) units |
Understanding the concept of circumference helps in various fields such as architecture, engineering, and everyday problem-solving where circular measurements are required.
Basic Formulas for Calculating Circumference
Calculating the circumference of a circle is straightforward using basic geometric formulas. The circumference, often denoted as \(C\), is the distance around the edge of a circle. There are two primary formulas to calculate the circumference, depending on whether you know the radius or the diameter of the circle.
Here are the basic formulas:
- Using the Radius (r): The radius is the distance from the center of the circle to any point on its edge.
- Formula: \(C = 2\pi r\)
- Explanation: Multiply the radius by 2 to get the diameter, then multiply by \( \pi \) to find the circumference.
- Using the Diameter (d): The diameter is the distance across the circle, passing through the center.
- Formula: \(C = \pi d\)
- Explanation: Directly multiply the diameter by \( \pi \) to find the circumference.
Let's break down these formulas with step-by-step examples:
- Example Using the Radius:
- Given: Radius (\(r\)) = 8 units
- Step 1: Multiply the radius by 2 to find the diameter: \(d = 2r = 2 \times 8 = 16\) units
- Step 2: Multiply the diameter by \( \pi \) to find the circumference: \(C = \pi \times 16 \approx 50.2655\) units
- Example Using the Diameter:
- Given: Diameter (\(d\)) = 10 units
- Step 1: Multiply the diameter by \( \pi \) to find the circumference: \(C = \pi \times 10 \approx 31.4159\) units
To summarize:
| Formula | Calculation | Example Result |
| \(C = 2\pi r\) | Radius (\(r\)) = 8 units | \(C \approx 50.2655\) units |
| \(C = \pi d\) | Diameter (\(d\)) = 10 units | \(C \approx 31.4159\) units |
Understanding these basic formulas allows you to easily calculate the circumference of any circle, whether you start with the radius or the diameter.
Components and Variables Explained
To fully understand how to calculate the perimeter of a circle, it's important to grasp the components and variables involved in the formula. These key elements include the radius, diameter, and the constant \( \pi \).
- Radius (r):
- Diameter (d):
- Pi (π):
The radius is the distance from the center of the circle to any point on its circumference. It is a crucial variable in calculating the circumference. The radius is denoted by the symbol \( r \). In the formula \( C = 2\pi r \), the radius is multiplied by 2 and \( \pi \) to find the circumference.
The diameter is the distance across the circle, passing through the center. It is twice the length of the radius. The diameter is denoted by the symbol \( d \). The relationship between the diameter and the radius is expressed as \( d = 2r \). In the formula \( C = \pi d \), the diameter is multiplied by \( \pi \) to find the circumference.
Pi (\( \pi \)) is a mathematical constant representing the ratio of a circle's circumference to its diameter. It is approximately equal to 3.14159. Pi is an irrational number, meaning it has an infinite number of decimal places without repeating. In both formulas for calculating circumference, \( \pi \) is used as a multiplier: \( C = 2\pi r \) and \( C = \pi d \).
To illustrate how these components work together, let's look at an example:
- Understanding \( \pi \): \( \pi \) is essential for calculating the circumference, as it provides the constant ratio needed for the formulas.
- Difference Between Radius and Diameter: The diameter is always twice the radius. This relationship is crucial in transforming one variable into another when using different formulas.
- Relation Between Circumference and Diameter: The circumference is directly proportional to the diameter. Using the formula \( C = \pi d \), you can see that the circumference increases linearly as the diameter increases.
Consider a circle with a radius of 5 units:
| Radius (r) | 5 units |
| Diameter (d) | \( d = 2 \times 5 = 10 \) units |
| Circumference (C) | \( C = 2\pi \times 5 = 10\pi \approx 31.4159 \) units |
Understanding these components and their relationships is essential for accurately calculating the perimeter of a circle.

Deriving the Formulas
Understanding the derivation of the formulas for the circumference of a circle helps in grasping the underlying geometry and mathematical concepts. Here, we will explore both historical and geometric perspectives on deriving these formulas.
Historical Perspective on \( \pi \)
The concept of \( \pi \) (\( \pi \)) has been known since ancient times. Mathematicians from various cultures approximated \( \pi \) by measuring circular objects and comparing their circumferences to their diameters. They discovered that the ratio remained constant, leading to the value we now recognize as \( \pi \approx 3.14159 \).
Geometric Derivation
The circumference of a circle is derived from the fundamental properties of a circle. Here's a step-by-step geometric derivation:
- Consider a Circle: Take a circle with a radius \( r \) and a diameter \( d = 2r \).
- Unwrapping the Circle: Imagine "unwrapping" the circle into a straight line. The length of this line is the circumference \( C \).
- Relating to Diameter: The unwrapped circle’s length is directly proportional to its diameter. Therefore, \( C = \pi d \).
- Substitute Diameter: Since \( d = 2r \), we can substitute \( 2r \) for \( d \) in the formula \( C = \pi d \).
- Final Formula: This substitution gives us \( C = \pi \times 2r \) or \( C = 2\pi r \).
To summarize, the formulas for circumference are:
- Using the Radius: \( C = 2\pi r \)
- Using the Diameter: \( C = \pi d \)
Let's see these derivations in action with an example:
| Given Radius (r) | 7 units |
| Calculate Diameter (d) | \( d = 2 \times 7 = 14 \) units |
| Using \( C = 2\pi r \) | \( C = 2 \times \pi \times 7 = 14\pi \approx 43.9823 \) units |
| Using \( C = \pi d \) | \( C = \pi \times 14 = 14\pi \approx 43.9823 \) units |
By understanding both the historical context and the geometric derivation, the formulas for finding the circumference of a circle become clearer and more intuitive.
Practical Examples and Problem Solving
Applying the formulas for calculating the circumference of a circle can be straightforward when following practical examples. Here, we'll explore three scenarios: when the radius is given, when the diameter is given, and when the circumference is given.
Example with Radius Given
Given: Radius (\( r \)) = 6 units
- Use the formula \( C = 2\pi r \).
- Substitute the given radius: \( C = 2 \times \pi \times 6 \).
- Calculate the result: \( C = 12\pi \approx 37.6991 \) units.
Therefore, the circumference of a circle with a radius of 6 units is approximately 37.6991 units.
Example with Diameter Given
Given: Diameter (\( d \)) = 10 units
- Use the formula \( C = \pi d \).
- Substitute the given diameter: \( C = \pi \times 10 \).
- Calculate the result: \( C = 10\pi \approx 31.4159 \) units.
Therefore, the circumference of a circle with a diameter of 10 units is approximately 31.4159 units.
Example with Circumference Given
Given: Circumference (\( C \)) = 50 units
- Use the formula \( C = 2\pi r \) to find the radius.
- Rearrange the formula to solve for \( r \): \( r = \frac{C}{2\pi} \).
- Substitute the given circumference: \( r = \frac{50}{2\pi} \).
- Calculate the result: \( r \approx \frac{50}{6.2832} \approx 7.9577 \) units.
Therefore, a circle with a circumference of 50 units has a radius of approximately 7.9577 units.
Let’s summarize these examples in a table for clarity:
| Given | Formula Used | Calculation | Result |
|---|---|---|---|
| Radius (\( r \)) = 6 units | \( C = 2\pi r \) | \( C = 2 \times \pi \times 6 \) | \( 12\pi \approx 37.6991 \) units |
| Diameter (\( d \)) = 10 units | \( C = \pi d \) | \( C = \pi \times 10 \) | \( 10\pi \approx 31.4159 \) units |
| Circumference (\( C \)) = 50 units | \( r = \frac{C}{2\pi} \) | \( r = \frac{50}{2\pi} \) | \( \approx 7.9577 \) units |
By following these examples, you can confidently solve problems involving the circumference of a circle, whether you start with the radius, diameter, or circumference.
Visual Representations
Visual representations help in understanding the concepts and formulas related to the circumference of a circle. Here, we will look at diagrams that illustrate the circle, radius, diameter, and how the circumference is calculated.
Diagram of a Circle
The following diagram shows a circle with its key components labeled:
- Center: The midpoint of the circle, usually denoted as \( O \).
- Radius (\( r \)): A line segment from the center of the circle to any point on its circumference.
- Diameter (\( d \)): A line segment passing through the center, connecting two points on the circumference. It is twice the length of the radius (\( d = 2r \)).

Illustrations of Radius and Diameter
The radius and diameter are fundamental in understanding the circumference:
- Radius (\( r \)): Any line segment from the center to the edge of the circle. Multiple radii can be drawn, all equal in length.
- Diameter (\( d \)): Any line segment passing through the center, connecting two points on the edge of the circle. The diameter is twice the radius.
The following illustration highlights the radius and diameter:

Visualizing the Circumference
The circumference is the distance around the circle. Visualize unwrapping the circle into a straight line to understand how the radius or diameter relates to the circumference.
Here is an illustration that helps in visualizing the circumference:

Consider the following step-by-step visual explanation:
- Step 1: Start with a circle with a known radius or diameter.
- Step 2: Unwrap the circle into a straight line. This line represents the circumference.
- Step 3: The length of the unwrapped line (circumference) can be calculated using the formulas \( C = 2\pi r \) or \( C = \pi d \).
By using visual aids and step-by-step illustrations, the concepts and calculations related to the circumference of a circle become more intuitive and easier to grasp.
Applications in Real Life
The formula for finding the perimeter of a circle, or its circumference, has numerous practical applications in various fields. Here, we explore its uses in architecture, engineering, and everyday life.
Uses in Architecture
Architects frequently use the circumference formula to design circular structures and features. Understanding the perimeter of circular elements ensures precise construction and aesthetics. Examples include:
- Domes: Calculating the circumference helps in planning the base of domes and curved surfaces.
- Columns: Designing round columns requires knowledge of their circumference for accurate material estimation and placement.
- Rotundas: Creating circular rooms or spaces involves using the circumference to determine dimensions and layout.
Role in Engineering
Engineers apply the circumference formula in various ways to ensure functionality and efficiency. Key applications include:
- Gear Design: Calculating the circumference of gears is crucial for ensuring proper meshing and operation in machinery.
- Pipeline Construction: Determining the circumference of pipes aids in calculating flow rates and material requirements.
- Rotary Engines: Designing rotary engines involves using the circumference to optimize performance and minimize wear.
Everyday Applications
In daily life, the concept of circumference is used more often than one might realize. Practical examples include:
- Measuring Wheels: The circumference of a wheel helps in determining the distance traveled per revolution, useful in vehicles and bicycles.
- Sports Equipment: Calculating the circumference of balls and other round equipment ensures they meet standard sizes for sports like basketball and soccer.
- Crafts and DIY Projects: Knowing the circumference is helpful in activities like creating circular tablecloths, knitting, or any project involving round objects.
To illustrate, consider the example of a circular garden path:
- Determine the Radius: Measure the radius of the garden path, say it is 4 meters.
- Calculate the Circumference: Use the formula \( C = 2\pi r \) to find the perimeter of the path. Here, \( C = 2 \times \pi \times 4 = 8\pi \approx 25.132 \) meters.
- Plan the Materials: With the circumference known, calculate the amount of edging material needed to outline the path.
These applications show how the formula for finding the perimeter of a circle is not just a mathematical concept but a practical tool used in various aspects of life and industry.

FAQs and Common Misconceptions
Here are some frequently asked questions and common misconceptions about the perimeter (circumference) of a circle:
1. What is the formula for the perimeter of a circle?
The formula to find the perimeter (circumference) of a circle depends on whether you know the radius or the diameter of the circle:
- If you know the radius (r): \( C = 2 \pi r \)
- If you know the diameter (d): \( C = \pi d \) (since \( d = 2r \))
2. What is \( \pi \) (pi)?
Pi (\( \pi \)) is a mathematical constant representing the ratio of a circle's circumference to its diameter. It is approximately equal to 3.14159, but it is often approximated as 3.14 or \(\frac{22}{7}\).
3. How can I find the radius if I know the circumference?
If you know the circumference (C) of a circle, you can find the radius (r) using the formula:
\( r = \frac{C}{2\pi} \)
Simply divide the circumference by \( 2\pi \).
4. What are common misconceptions about the perimeter of a circle?
- Misconception 1: The terms 'perimeter' and 'circumference' are often used interchangeably for circles, but 'perimeter' generally refers to polygons.
- Misconception 2: Some people believe \( \pi \) is exactly 3.14, but it is an irrational number with a non-repeating, non-terminating decimal expansion.
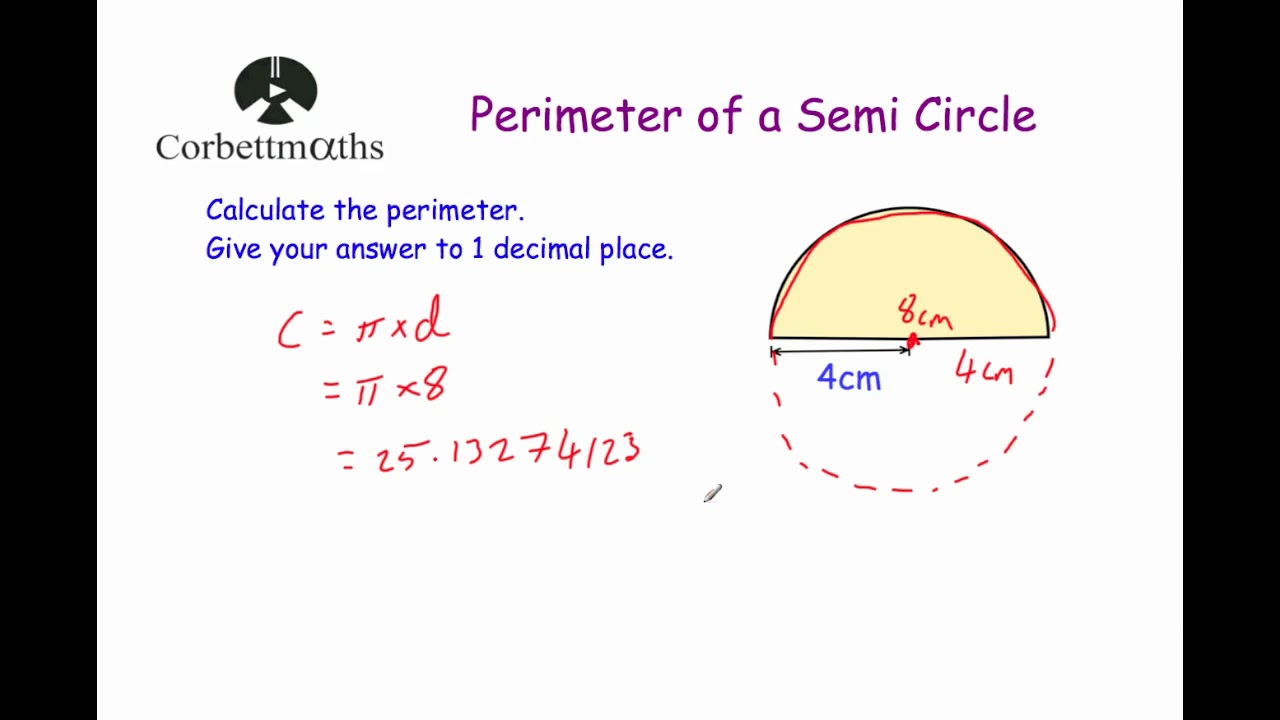
5. How do you calculate the perimeter of a semi-circle?
The perimeter of a semi-circle includes the half circumference plus the diameter:
\( \text{Perimeter} = \pi r + 2r \)
6. How does the formula change if the circle is not perfect?
If the shape is not a perfect circle, the term 'circumference' no longer applies, as the formula \( C = 2\pi r \) is specific to perfect circles.
7. Can the value of \( \pi \) vary?
No, \( \pi \) is a constant value. Its decimal representation can be truncated or approximated for practical calculations, but its true value remains the same.
8. Is the circumference always greater than the diameter?
Yes, because \( C = \pi d \) and \( \pi \) is approximately 3.14, the circumference will always be about three times greater than the diameter.
9. What are practical applications of the circumference formula?
- In construction and engineering to determine the length of materials needed to go around circular objects.
- In everyday life, such as calculating the distance around circular tracks or objects.
Understanding these fundamental aspects of the perimeter (circumference) of a circle helps clarify common doubts and ensures accurate calculations in various applications.
Advanced Topics Related to Circle Perimeter
The concept of the perimeter of a circle, also known as the circumference, extends into various advanced topics and applications. This section explores some of these topics in detail.
Calculating the Perimeter of Semi-Circles
A semi-circle is half of a circle. To calculate the perimeter of a semi-circle, you need to account for both the curved part and the straight edge (diameter).
Formula:
\[ \text{Perimeter} = \pi r + 2r \]
where \( r \) is the radius.
This formula includes the half-circumference \( \pi r \) and the diameter \( 2r \).
Perimeter of Complex Circular Shapes
Circular shapes can have additional features such as sectors and segments. Calculating the perimeter of these shapes involves more advanced formulas:
Perimeter of a Sector
A sector is a portion of a circle enclosed by two radii and an arc. The perimeter (or arc length) of a sector can be calculated using:
\[ \text{Perimeter} = r \theta + 2r \]
where \( r \) is the radius and \( \theta \) is the central angle in radians.
Perimeter of a Segment
A segment is a region of a circle bounded by a chord and the corresponding arc. The perimeter of a segment includes the arc length and the chord length:
\[ \text{Perimeter} = r \theta + 2r \sin\left(\frac{\theta}{2}\right) \]
where \( \theta \) is the central angle in radians.
Using Area to Find Circumference
In some cases, you may know the area of a circle but not its radius or diameter. You can still find the circumference using the area with the following formula:
\[ C = 2\sqrt{\pi A} \]
where \( C \) is the circumference and \( A \) is the area of the circle.
Geometric Derivations and Historical Context
The value of \( \pi \) (pi) is crucial in the calculation of the circumference. Historically, various mathematicians have approximated \( \pi \) through geometric methods:
- Archimedes' method of inscribing and circumscribing polygons around a circle.
- The use of infinite series in calculus to derive more accurate values of \( \pi \).
Applications in Real Life
The perimeter of circles and semi-circles is widely used in various fields:
- Architecture: Designing arches, domes, and round structures.
- Engineering: Calculating material lengths for pipes, wheels, and gears.
- Everyday Applications: Measuring distances around circular tracks, gardens, and fountains.
Conclusion and Summary
Understanding the perimeter, or circumference, of a circle is fundamental in geometry. The circumference is the distance around the circle and can be calculated using the formulas:
- Using the radius: \( C = 2\pi r \)
- Using the diameter: \( C = \pi d \)
Here, \( r \) represents the radius, \( d \) represents the diameter, and \( \pi \) (Pi) is approximately 3.14159. These formulas highlight the direct relationship between the circle's radius, diameter, and its circumference.
Additionally, the concept of \( \pi \) is critical as it represents the ratio of the circumference of any circle to its diameter. This constant is integral not only in calculating the circumference but also in understanding other geometric properties of circles.
For practical applications, knowing how to derive the perimeter of a circle allows for solving real-world problems, such as determining the length of a boundary or the amount of material needed to cover the edge of a circular object.
We also explored advanced topics like the perimeter of semicircles and segments, emphasizing the versatility of these calculations in various fields including architecture, engineering, and everyday life.
In summary, mastering the formulas and understanding the variables involved in calculating the perimeter of a circle is essential for both academic purposes and practical applications. This knowledge forms the basis for further studies in geometry and its applications in numerous disciplines.
Làm Thế Nào Để Tính Chu Vi Hình Tròn Từ Đường Kính
READ MORE:
Làm Thế Nào Để Tính Chu Vi Hình Tròn