Topic b+-square root b2-4ac 2a: Unlock the secrets of solving quadratic equations with the powerful quadratic formula, b+-square root b2-4ac 2a. This comprehensive guide will take you step-by-step through the process, ensuring you master the method and apply it confidently. Whether you're a student or math enthusiast, this article will enhance your understanding and skills.
Table of Content
- Quadratic Formula
- Introduction to Quadratic Equations
- Derivation of the Quadratic Formula
- Understanding the Components of the Formula
- Steps to Solve Quadratic Equations Using the Quadratic Formula
- Analyzing the Discriminant
- Examples of Solving Quadratic Equations
- Special Cases of Quadratic Equations
- Graphical Interpretation of Quadratic Equations
- Applications of Quadratic Equations in Real Life
- Common Mistakes and How to Avoid Them
- Practice Problems and Solutions
- Additional Resources and Further Reading
- YOUTUBE: Xem video này để học cách đánh giá một biểu thức trong dạng (b^2-4ac)/(2a). Video sẽ giúp bạn hiểu rõ hơn về cách tính toán và áp dụng công thức này.
Quadratic Formula
The quadratic formula is used to find the solutions to a quadratic equation of the form \(ax^2 + bx + c = 0\). The solutions are given by:
Steps to Solve a Quadratic Equation Using the Quadratic Formula
- Identify the coefficients \(a\), \(b\), and \(c\) in the quadratic equation \(ax^2 + bx + c = 0\).
- Compute the discriminant, \(b^2 - 4ac\).
- Substitute the values of \(a\), \(b\), and \(c\) into the quadratic formula:
- Simplify the expression under the square root (the discriminant).
- Simplify the fractions to find the two possible solutions for \(x\).
Discriminant Analysis
The value of the discriminant \(b^2 - 4ac\) determines the nature of the roots:
- If \(b^2 - 4ac > 0\), there are two distinct real roots.
- If \(b^2 - 4ac = 0\), there is one real root (repeated).
- If \(b^2 - 4ac < 0\), there are two complex roots.
Example
Consider the quadratic equation \(2x^2 + 3x - 2 = 0\).
Here, \(a = 2\), \(b = 3\), and \(c = -2\). Using the quadratic formula:
Calculate the discriminant:
So, the solutions are:
This gives two solutions:

READ MORE:
Introduction to Quadratic Equations
Quadratic equations are polynomial equations of the second degree, generally represented in the form:
\( ax^2 + bx + c = 0 \)
where \(a\), \(b\), and \(c\) are constants, with \(a \neq 0\). The term \(ax^2\) is the quadratic term, \(bx\) is the linear term, and \(c\) is the constant term.
Quadratic equations are fundamental in algebra and appear frequently in various branches of mathematics, physics, engineering, and many real-life applications. The solutions to quadratic equations can be found using several methods, including:
- Factoring
- Completing the Square
- Using the Quadratic Formula
- Graphing
The quadratic formula is a universally applicable method for solving quadratic equations, and it is derived from the standard form of a quadratic equation. The formula is:
\( x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{{2a}} \)
This formula provides the solutions (roots) of the quadratic equation by substituting the values of \(a\), \(b\), and \(c\) from the given quadratic equation. The term under the square root, \(b^2 - 4ac\), is called the discriminant, which determines the nature of the roots:
- If \(b^2 - 4ac > 0\), the equation has two distinct real roots.
- If \(b^2 - 4ac = 0\), the equation has exactly one real root (a repeated root).
- If \(b^2 - 4ac < 0\), the equation has two complex roots.
Understanding how to solve quadratic equations and the significance of the discriminant is crucial for tackling more complex mathematical problems and applications. In the subsequent sections, we will delve deeper into the derivation of the quadratic formula, analyze the components, and explore various examples to solidify our understanding.
Derivation of the Quadratic Formula
To derive the quadratic formula, we start with a general quadratic equation in the form:
\( ax^2 + bx + c = 0 \)
Our goal is to solve for \( x \). The quadratic formula is obtained by using the method of completing the square. Here’s a step-by-step derivation:
- Divide through by \( a \):
- Isolate the constant term on the right side:
- Add the square of half the coefficient of \( x \) to both sides to complete the square:
- Rewrite the left side as a perfect square trinomial:
- Combine the fractions on the right side:
- Take the square root of both sides:
- Isolate \( x \) by subtracting \( \frac{b}{2a} \) from both sides:
- Combine the fractions into a single expression:
\( x^2 + \frac{b}{a} x + \frac{c}{a} = 0 \)
\( x^2 + \frac{b}{a} x = -\frac{c}{a} \)
\( x^2 + \frac{b}{a} x + \left(\frac{b}{2a}\right)^2 = \left(\frac{b}{2a}\right)^2 - \frac{c}{a} \)
\( \left( x + \frac{b}{2a} \right)^2 = \frac{b^2}{4a^2} - \frac{c}{a} \)
\( \left( x + \frac{b}{2a} \right)^2 = \frac{b^2 - 4ac}{4a^2} \)
\( x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 - 4ac}}{2a} \)
\( x = -\frac{b}{2a} \pm \frac{\sqrt{b^2 - 4ac}}{2a} \)
\( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)
This final expression is the quadratic formula, which gives the solutions to any quadratic equation \( ax^2 + bx + c = 0 \).
Understanding the Components of the Formula
The quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \) is used to find the roots of a quadratic equation \( ax^2 + bx + c = 0 \). Let's break down the components of this formula to understand their roles and meanings:
- Coefficient \( a \): This is the coefficient of the \( x^2 \) term in the quadratic equation. It determines the "width" and direction of the parabola. If \( a \) is positive, the parabola opens upwards; if \( a \) is negative, it opens downwards.
- Coefficient \( b \): This is the coefficient of the \( x \) term. It affects the location of the vertex of the parabola and influences the symmetry of the quadratic function.
- Constant \( c \): This is the constant term in the quadratic equation. It represents the y-intercept of the quadratic function, which is the point where the graph intersects the y-axis.
- Discriminant \( b^2 - 4ac \): This part of the formula under the square root sign determines the nature of the roots. It tells us how many and what type of solutions we have:
- If \( b^2 - 4ac > 0 \), there are two distinct real roots.
- If \( b^2 - 4ac = 0 \), there is exactly one real root (a repeated root).
- If \( b^2 - 4ac < 0 \), there are two complex conjugate roots.
- Term \( -b \): This represents the horizontal shift of the roots along the x-axis. It is part of the numerator and affects the root values directly.
- Square root \( \sqrt{b^2 - 4ac} \): This term determines the distance between the roots and the axis of symmetry of the parabola. It adds or subtracts this value from \( -b \).
- Division by \( 2a \): This normalizes the expression by the leading coefficient \( a \), adjusting for the "scale" of the quadratic equation. It ensures the final roots are correctly positioned relative to the parabola's width and direction.
- Plus-minus symbol \( \pm \): This indicates that there are two possible values for \( x \), representing the two roots of the quadratic equation. One root is found by adding the square root term, and the other by subtracting it.
By understanding each component of the quadratic formula, we can gain deeper insight into the behavior and solutions of quadratic equations.
Steps to Solve Quadratic Equations Using the Quadratic Formula
The quadratic formula is used to find the solutions of a quadratic equation of the form \(ax^2 + bx + c = 0\). The formula is:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
Follow these steps to solve quadratic equations using the quadratic formula:
- Identify the coefficients: In the quadratic equation \(ax^2 + bx + c = 0\), identify the coefficients \(a\), \(b\), and \(c\).
- Calculate the discriminant: Compute the value of the discriminant using the formula: \[ \Delta = b^2 - 4ac \] The discriminant will help determine the nature of the roots.
- Analyze the discriminant:
- If \(\Delta > 0\), the equation has two distinct real roots.
- If \(\Delta = 0\), the equation has exactly one real root (repeated root).
- If \(\Delta < 0\), the equation has two complex roots.
- Apply the quadratic formula: Substitute the values of \(a\), \(b\), and \(\Delta\) into the quadratic formula: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \] Solve for the roots \(x_1\) and \(x_2\).
- Simplify the results: Simplify the expression under the square root and the fraction to find the exact values of the roots.
Let's look at an example to illustrate these steps:
Example: Solve \(2x^2 + 3x - 2 = 0\)
- Identify the coefficients: \(a = 2\), \(b = 3\), \(c = -2\)
- Calculate the discriminant: \[ \Delta = b^2 - 4ac = 3^2 - 4(2)(-2) = 9 + 16 = 25 \]
- Analyze the discriminant: \(\Delta = 25 > 0\), so there are two distinct real roots.
- Apply the quadratic formula: \[ x = \frac{-3 \pm \sqrt{25}}{2 \cdot 2} = \frac{-3 \pm 5}{4} \] Solving this, we get: \[ x_1 = \frac{-3 + 5}{4} = \frac{2}{4} = \frac{1}{2} \] \[ x_2 = \frac{-3 - 5}{4} = \frac{-8}{4} = -2 \]
- Simplify the results: The roots are \(x_1 = \frac{1}{2}\) and \(x_2 = -2\).
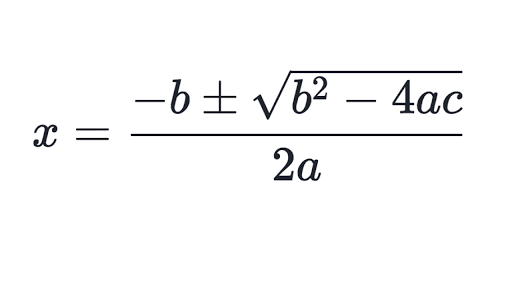
Analyzing the Discriminant
The discriminant of a quadratic equation \(ax^2 + bx + c = 0\) is a key component in determining the nature of the roots. It is given by the expression:
\[
\Delta = b^2 - 4ac
\]
Here's how to analyze the discriminant step by step:
- Identify the coefficients: In the quadratic equation \(ax^2 + bx + c = 0\), identify the coefficients \(a\), \(b\), and \(c\).
- Calculate the discriminant: Compute the value of the discriminant using the formula: \[ \Delta = b^2 - 4ac \] This value will help determine the nature of the roots.
- Interpret the discriminant: Based on the value of \(\Delta\), the roots of the quadratic equation can be determined as follows:
- If \(\Delta > 0\), the equation has two distinct real roots. This means the parabola intersects the x-axis at two points.
- If \(\Delta = 0\), the equation has exactly one real root (a repeated root). This means the parabola touches the x-axis at one point (the vertex).
- If \(\Delta < 0\), the equation has two complex roots. This means the parabola does not intersect the x-axis.
Let's look at examples for each case to illustrate:
| Example | Equation | Discriminant Calculation | Nature of Roots |
|---|---|---|---|
| 1 | \(x^2 - 3x + 2 = 0\) | \[ \Delta = (-3)^2 - 4(1)(2) = 9 - 8 = 1 \] | Two distinct real roots |
| 2 | \(x^2 - 4x + 4 = 0\) | \[ \Delta = (-4)^2 - 4(1)(4) = 16 - 16 = 0 \] | One real repeated root |
| 3 | \(x^2 + x + 1 = 0\) | \[ \Delta = 1^2 - 4(1)(1) = 1 - 4 = -3 \] | Two complex roots |
By analyzing the discriminant, you can predict the nature of the roots without actually solving the quadratic equation.
Examples of Solving Quadratic Equations
Let's go through some detailed examples of solving quadratic equations using the quadratic formula. The quadratic formula is:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
Here are a few examples:
Example 1: \(x^2 - 5x + 6 = 0\)
- Identify the coefficients: \(a = 1\), \(b = -5\), \(c = 6\).
- Calculate the discriminant: \[ \Delta = b^2 - 4ac = (-5)^2 - 4(1)(6) = 25 - 24 = 1 \]
- Since \(\Delta > 0\), there are two distinct real roots.
- Apply the quadratic formula: \[ x = \frac{-(-5) \pm \sqrt{1}}{2(1)} = \frac{5 \pm 1}{2} \]
- Simplify to find the roots: \[ x_1 = \frac{5 + 1}{2} = \frac{6}{2} = 3 \] \[ x_2 = \frac{5 - 1}{2} = \frac{4}{2} = 2 \]
- The roots are \(x_1 = 3\) and \(x_2 = 2\).
Example 2: \(2x^2 + 4x + 2 = 0\)
- Identify the coefficients: \(a = 2\), \(b = 4\), \(c = 2\).
- Calculate the discriminant: \[ \Delta = b^2 - 4ac = 4^2 - 4(2)(2) = 16 - 16 = 0 \]
- Since \(\Delta = 0\), there is one repeated real root.
- Apply the quadratic formula: \[ x = \frac{-4 \pm \sqrt{0}}{2(2)} = \frac{-4}{4} = -1 \]
- The repeated root is \(x = -1\).
Example 3: \(x^2 + 2x + 5 = 0\)
- Identify the coefficients: \(a = 1\), \(b = 2\), \(c = 5\).
- Calculate the discriminant: \[ \Delta = b^2 - 4ac = 2^2 - 4(1)(5) = 4 - 20 = -16 \]
- Since \(\Delta < 0\), there are two complex roots.
- Apply the quadratic formula: \[ x = \frac{-2 \pm \sqrt{-16}}{2(1)} = \frac{-2 \pm 4i}{2} = -1 \pm 2i \]
- The roots are \(x_1 = -1 + 2i\) and \(x_2 = -1 - 2i\).
By following these examples, you can solve any quadratic equation using the quadratic formula. Remember to always start by identifying the coefficients and calculating the discriminant to understand the nature of the roots.
Special Cases of Quadratic Equations
Quadratic equations in the standard form \( ax^2 + bx + c = 0 \) have several special cases based on the values of coefficients \( a \), \( b \), and \( c \).
- Perfect Square Trinomial: When the discriminant \( \Delta = b^2 - 4ac \) equals zero, the quadratic equation has a double root, indicating that both solutions are identical. Mathematically, this occurs when the equation can be factored into a perfect square, such as \( (mx + n)^2 = 0 \).
- Real and Equal Roots: This case arises when \( \Delta > 0 \) and the roots of the quadratic equation are distinct but equal in magnitude, often represented as \( x = \frac{{-b \pm \sqrt{b^2 - 4ac}}}{{2a}} \).
- Real and Unequal Roots: When \( \Delta > 0 \), the quadratic equation has two distinct real roots that differ in value.
- Complex Roots: If \( \Delta < 0 \), the roots of the quadratic equation are complex numbers, usually in the form \( x = \frac{{-b \pm \sqrt{b^2 - 4ac}i}}{{2a}} \), where \( i \) is the imaginary unit.
- Linear Equation: When \( a = 0 \) and \( b \neq 0 \), the quadratic equation reduces to a linear equation \( bx + c = 0 \), resulting in a single solution.
- Constant Equation: If both \( a = 0 \) and \( b = 0 \), the equation \( c = 0 \) holds true for all \( x \), meaning every real number is a solution.
Graphical Interpretation of Quadratic Equations
Graphically, quadratic equations represent parabolas, which are U-shaped curves on the coordinate plane.
- Vertex: The vertex of a parabola given by \( ax^2 + bx + c \) occurs at \( x = -\frac{b}{2a} \) and can be found using the formula for the axis of symmetry.
- Direction and Shape: The coefficient \( a \) determines whether the parabola opens upwards (\( a > 0 \)) or downwards (\( a < 0 \)).
- Intercepts:
- y-Intercept: The y-intercept of the parabola is at \( (0, c) \).
- x-Intercepts: The roots of the quadratic equation \( ax^2 + bx + c = 0 \) correspond to the x-coordinates where the parabola intersects the x-axis.
- Vertex Form: The vertex form of a quadratic equation \( a(x - h)^2 + k \) explicitly shows the vertex \( (h, k) \) and the direction of opening.
- Discriminant and Nature of Roots: The discriminant \( \Delta = b^2 - 4ac \) determines the nature of the roots and hence how the parabola intersects the x-axis.
- Axis of Symmetry: The line \( x = -\frac{b}{2a} \) divides the parabola symmetrically.

Applications of Quadratic Equations in Real Life
Quadratic equations are widely used in various real-life applications to model and solve problems involving quadratic relationships.
- Physics: Projectile motion of objects such as projectiles, balls, and rockets follow a parabolic path described by quadratic equations.
- Engineering: Structural engineers use quadratic equations to determine the dimensions of arches and bridges, which involve parabolic curves for optimal design.
- Economics: Quadratic equations are used in economics to model revenue, profit, cost functions, and optimization problems.
- Biology: Population growth of species can be modeled using quadratic equations, especially when considering factors like birth rate, death rate, and carrying capacity.
- Computer Graphics: In computer graphics, quadratic equations are used to define curves and surfaces, such as Bezier curves and parabolic shapes.
- Finance: Quadratic equations are utilized in finance for various applications, including compound interest calculations and portfolio optimization.
- Optics: Quadratic equations describe the focal length and properties of lenses and mirrors in optics, essential for designing optical instruments.
- Statistics: In statistics, quadratic regression models are used to fit curves to data points and make predictions based on quadratic relationships.
Common Mistakes and How to Avoid Them
Understanding and solving quadratic equations can sometimes lead to common errors, which can be avoided with careful attention to details and methods.
- Misinterpreting the Quadratic Formula: Ensure correct usage of the quadratic formula \( x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{{2a}} \) and its components.
- Errors in Calculating the Discriminant: Double-check calculations for the discriminant \( \Delta = b^2 - 4ac \) to accurately determine the nature of roots.
- Incorrect Application of Signs: Pay close attention to signs when substituting values into the quadratic formula to avoid computational mistakes.
- Forgetting Special Cases: Remember to consider special cases such as perfect square trinomials or equations that reduce to linear or constant forms.
- Ignoring Graphical Interpretation: Utilize graphical methods to verify solutions and understand the behavior of quadratic equations visually.
- Skipping Verification of Solutions: Always verify obtained solutions by substituting back into the original equation to ensure correctness.
- Overlooking Algebraic Simplification: Simplify algebraic steps carefully to avoid errors in manipulating quadratic expressions.
- Not Checking for Extraneous Solutions: Be cautious of solutions that may satisfy derived equations but not the original quadratic equation.
Practice Problems and Solutions
Practice solving quadratic equations with these problems, along with detailed step-by-step solutions to guide your understanding.
- Solve the quadratic equation \( 3x^2 - 4x + 1 = 0 \).
- Determine the roots of \( 2x^2 + 5x - 3 = 0 \).
- Find the solutions for \( x^2 - 9 = 0 \).
- Solve \( 4x^2 - 12x = 0 \) and identify any special cases.
- Calculate the roots of \( x^2 + 4x + 4 = 0 \) and interpret the discriminant.
- Find the values of \( x \) for \( x^2 + 6x + 9 = 0 \) and explain the nature of the solutions.
- Solve \( 2x^2 - 7x - 15 = 0 \) using the quadratic formula and verify your solutions.
- Determine the solutions to \( x^2 - 2x - 8 = 0 \) and check for any mistakes in the calculation.
Additional Resources and Further Reading
Explore more about quadratic equations with these recommended resources and further readings.

Xem video này để học cách đánh giá một biểu thức trong dạng (b^2-4ac)/(2a). Video sẽ giúp bạn hiểu rõ hơn về cách tính toán và áp dụng công thức này.
Ví dụ: Đánh giá một Biểu thức trong Dạng (b^2-4ac)/(2a)
READ MORE:
Xem video này để học cách giải phương trình bậc hai bằng công thức tổng quát. Video sẽ giúp bạn hiểu rõ hơn về cách tính toán và áp dụng công thức này.
Phương trình bậc hai bằng công thức tổng quát