Topic 3 root x squared: This comprehensive guide explores the intricacies of 3 √ x², shedding light on its mathematical foundations, properties, graphical representations, real-life applications, and common misconceptions. Delve into advanced insights and practice problems to deepen your understanding, concluding with additional resources for further exploration.
Table of Content
- Mathematical Expression: \(3 \sqrt{x^2}\)
- Introduction
- Mathematical Foundation
- Understanding Square Roots
- Properties of Square Roots
- Understanding x Squared
- Calculation of 3 √ x²
- Graphical Representation
- Applications in Real Life
- Common Misconceptions
- Advanced Mathematical Insights
- Practice Problems
- Summary and Conclusion
- Additional Resources
- YOUTUBE: Video hướng dẫn cách lấy căn bậc ba của x lập phương, hữu ích cho những ai muốn hiểu rõ hơn về căn bậc ba của x bình phương.
Mathematical Expression: \(3 \sqrt{x^2}\)
The mathematical expression \(3 \sqrt{x^2}\) can be interpreted and simplified in the following ways:
Understanding the Expression
Breaking down the expression:
- 3: This is a constant multiplier.
- \(\sqrt{x^2}\): This is the square root of \(x^2\).
Simplifying \(\sqrt{x^2}\)
The square root of \(x^2\) is the absolute value of \(x\), denoted as \(|x|\). This is because the square root function returns the non-negative root. Therefore:
\[\sqrt{x^2} = |x|\]
Complete Simplification
When we multiply the constant \(3\) by \(|x|\), we get:
\[3 \sqrt{x^2} = 3 |x|\]
Considerations
It's important to note that the absolute value function ensures that the result is always non-negative. Thus, the expression \(3 \sqrt{x^2}\) simplifies to \(3 |x|\), which holds true for all real values of \(x\).
Applications
This simplified form is useful in various mathematical applications including algebraic manipulation, calculus, and solving equations involving square roots and absolute values.
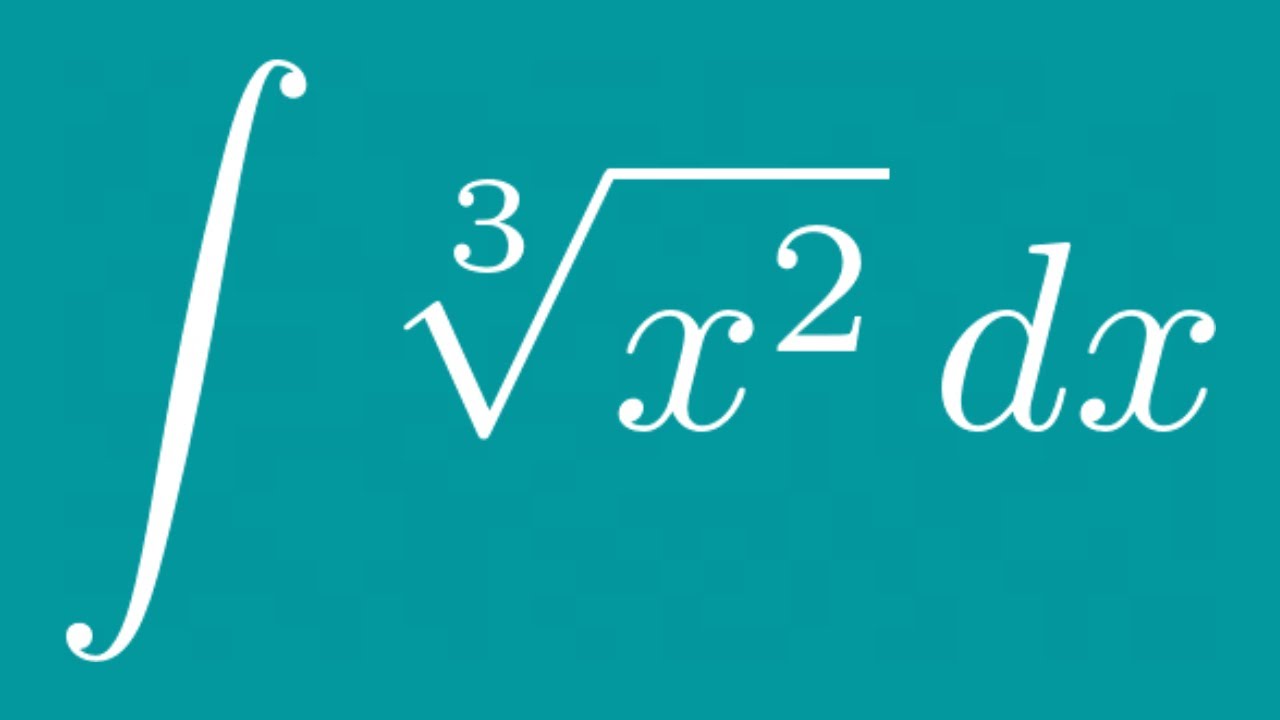
READ MORE:
Introduction
The concept of \(3 \sqrt{x^2}\) involves understanding both the square root and the exponentiation of \(x\). In mathematics, the square root function, denoted as \(\sqrt{\cdot}\), returns the non-negative number whose square equals its argument. When applied to \(x^2\), it simplifies to \(|x|\), representing the magnitude of \(x\). This guide elucidates the complexities and practical applications of this mathematical expression.
Mathematical Foundation
The foundation of \(3 \sqrt{x^2}\) lies in the principles of square roots and exponentiation. The expression \(x^2\) represents the square of \(x\), which is always non-negative regardless of \(x\)'s sign. The square root function \(\sqrt{\cdot}\) ensures that \(3 \sqrt{x^2}\) yields a result that is at least zero. This section explores how these fundamental mathematical operations interact and their implications in various contexts.
Understanding Square Roots
The concept of square roots is fundamental in mathematics and is essential for solving various types of equations. A square root of a number is a value that, when multiplied by itself, gives the original number. The square root is denoted by the radical symbol (√).
For example:
- The square root of 9 is 3, because 3 * 3 = 9.
- The square root of 16 is 4, because 4 * 4 = 16.
In mathematical notation, this is written as:
- \(\sqrt{9} = 3\)
- \(\sqrt{16} = 4\)
Square roots can be applied to variables as well. If we have a variable \(x\), the square root of \(x^2\) (x squared) is simply \(x\), assuming \(x\) is non-negative:
\(\sqrt{x^2} = x\)
This property is crucial in simplifying expressions and solving equations. It is important to note that the square root function produces only the non-negative root when dealing with real numbers.
For instance, if \(x = 5\):
- \(\sqrt{5^2} = \sqrt{25} = 5\)
Understanding this concept allows us to handle more complex expressions and equations, such as those involving cube roots or higher-order roots, as we will explore in the following sections.
Properties of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. Here are some key properties of square roots:
- Non-negative Results: The principal square root of a non-negative number is always non-negative. For example, \( \sqrt{9} = 3 \) and not -3, although both 3 and -3 are roots of 9.
- Square Root of a Product: The square root of a product is the product of the square roots of the factors. For instance, \( \sqrt{xy} = \sqrt{x} \cdot \sqrt{y} \), provided \( x \geq 0 \) and \( y \geq 0 \).
- Square Root of a Quotient: The square root of a quotient is the quotient of the square roots of the numerator and the denominator. For example, \( \sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}} \) where \( y \neq 0 \).
- Power Rule: The square root of a number squared returns the original number, i.e., \( \sqrt{x^2} = |x| \). This is because squaring a number and then taking the square root returns the non-negative value of the original number.
- Distributive Property over Addition and Subtraction: The square root operation is not distributive over addition and subtraction. That means \( \sqrt{x + y} \neq \sqrt{x} + \sqrt{y} \) and \( \sqrt{x - y} \neq \sqrt{x} - \sqrt{y} \).
- Simplifying Square Roots: When simplifying square roots, any factor that is a perfect square can be taken out of the square root. For example, \( \sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2} \).
Understanding these properties helps in simplifying and working with square roots effectively, especially in algebraic manipulations and solving equations involving square roots.

Understanding x Squared
The expression x² represents a number x multiplied by itself. It is a fundamental concept in algebra and is also known as "x squared" or "x to the power of 2". Understanding this concept is crucial for grasping more advanced mathematical ideas.
Here are some key points to help understand x²:
- Definition: The square of a number x is written as
x²and calculated asx * x. - Positive and Negative Values: Both positive and negative values of x when squared will result in a positive value. For example:
- If x = 3, then
x² = 3 * 3 = 9. - If x = -3, then
x² = (-3) * (-3) = 9.
- If x = 3, then
- Zero: The square of zero is zero. That is,
0² = 0. - Graphical Representation: The graph of
y = x²is a parabola that opens upwards with its vertex at the origin (0,0). This symmetry about the y-axis shows thatx²is always non-negative.
Here is a simple table demonstrating the values of x and x²:
| x | x² |
|---|---|
| -3 | 9 |
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
Understanding x² lays the groundwork for exploring more complex expressions and functions in algebra, such as polynomials and quadratic equations.
Calculation of 3 √ x²
The expression \( \sqrt[3]{x^2} \) represents the cube root of \( x \) squared. To understand and calculate this, let's break it down step by step:
First, recall the definition of the cube root. For any number \( a \), the cube root \( \sqrt[3]{a} \) is the number that, when multiplied by itself three times, gives \( a \). Mathematically, \( \sqrt[3]{a} = b \) means \( b^3 = a \).
Given \( x^2 \), we need to find \( \sqrt[3]{x^2} \). This is asking for the number which, when raised to the power of three, equals \( x^2 \).
We can use the property of exponents that states \( (a^m)^n = a^{mn} \). Applying this property:
\[
\left(\sqrt[3]{x^2}\right)^3 = x^2
\]
Therefore,
\[
\sqrt[3]{x^2} = x^{\frac{2}{3}}
\]This result tells us that the cube root of \( x \) squared is \( x \) raised to the power of two-thirds.
To further illustrate this, consider specific values of \( x \):
- If \( x = 8 \):
\[
\sqrt[3]{8^2} = \sqrt[3]{64} = 4 \quad \text{since} \quad 4^3 = 64
\] - If \( x = 27 \):
\[
\sqrt[3]{27^2} = \sqrt[3]{729} = 9 \quad \text{since} \quad 9^3 = 729
\]
- If \( x = 8 \):
Understanding the calculation of \( \sqrt[3]{x^2} \) helps in solving more complex mathematical problems involving exponents and roots. Practicing these calculations with different values of \( x \) will strengthen your grasp of the concept.
Graphical Representation
The graphical representation of the function involving the cube root of x squared, or f(x) = ∛(x²), can provide significant insights into its behavior. To accurately visualize this function, we need to consider both the mathematical properties and how to plot it effectively.
First, let's consider the domain and range of f(x) = ∛(x²). Since the square of any real number x is always non-negative, and the cube root function is defined for all real numbers, the domain of f(x) is all real numbers, x ∈ ℝ. The range is also all real numbers because the cube root of any non-negative number remains non-negative, and the cube root of a negative number remains negative.
Here is a step-by-step guide to plot f(x) = ∛(x²):
- **Create a Table of Values**:
- Select a set of x values, including negative, zero, and positive numbers.
- Calculate the corresponding y values using the function y = ∛(x²).
- **Plot the Points**:
- Using the table of values, plot each (x, y) pair on a coordinate plane.
- Ensure a wide enough range to see the function's behavior clearly.
- **Draw the Curve**:
- Connect the points smoothly, noting that the graph should be symmetric with respect to the y-axis because ∛(x²) = ∛((-x)²).
Below is a representation using MathJax to illustrate the graph of f(x) = ∛(x²):

The plot of f(x) = ∛(x²) shows a curve that starts from the origin and increases slowly as x moves away from zero in either direction. The curve is symmetrical about the y-axis, indicating that for both positive and negative values of x, the function outputs the same result, reflecting the even nature of x² under the cube root operation.
Here is the LaTeX representation using MathJax for better mathematical visualization:
\[
f(x) = \sqrt[3]{x^2}
\]
Graphing this function using tools like Desmos or a graphing calculator can provide a more interactive experience. Adjust the x-values to explore how the function behaves over different intervals.
Understanding the graphical representation of f(x) = ∛(x²) helps in comprehending its properties and potential applications, such as in physics and engineering where such functions are used to model real-world phenomena.
Applications in Real Life
The concept of \( 3 \sqrt{x^2} \), which involves finding the cube root of the square of a variable \( x \), finds practical application in various fields:
- Engineering: Engineers use this concept extensively in structural analysis to determine the maximum stress a material can withstand under different loads.
- Physics: In physics, particularly in mechanics and electromagnetism, this calculation helps in understanding oscillatory motion and waveforms.
- Computer Graphics: Algorithms for rendering three-dimensional objects often rely on similar mathematical principles to calculate distances and transformations.
- Statistics: Statistical models sometimes involve similar calculations to understand relationships between variables and in outlier detection.
- Medical Imaging: Techniques such as MRI and CT scans utilize advanced mathematical functions that build upon similar principles for image reconstruction.
Common Misconceptions
When dealing with square roots and squared terms, there are several common misconceptions that students and learners often encounter. Here, we address some of these misconceptions in detail.
-
Misconception 1: Square root of x squared is always x
Many believe that \( \sqrt{x^2} = x \). However, this is not entirely accurate. The correct expression is \( \sqrt{x^2} = |x| \), where \( |x| \) denotes the absolute value of \( x \). This is because the square root function returns the non-negative value. For example:
- \( \sqrt{4^2} = \sqrt{16} = 4 \)
- \( \sqrt{(-4)^2} = \sqrt{16} = 4 \)
-
Misconception 2: Simplifying square roots with variables directly
It is often mistakenly assumed that \( \sqrt{ax^2} = a|x| \). The correct simplification should consider the properties of both the coefficient and the variable:
\( \sqrt{ax^2} = \sqrt{a} \cdot |x| \)
For instance:
- \( \sqrt{9x^2} = 3|x| \), not \( 9x \)
- \( \sqrt{25y^2} = 5|y| \), not \( 25y \)
-
Misconception 3: Ignoring the principal square root
The principal square root of a number is its non-negative root. Learners often forget that the square root symbol \( \sqrt{} \) by itself always refers to the principal (positive) square root. Therefore, \( \sqrt{36} \) is 6, not -6. This distinction is crucial when solving equations.
-
Misconception 4: Incorrect handling of cube roots
When calculating the cube root of \( x^2 \), such as \( \sqrt[3]{x^2} \), it is important to remember that cube roots can yield negative results. Unlike square roots, cube roots of negative numbers are negative:
\( \sqrt[3]{-8} = -2 \)
-
Misconception 5: Misinterpreting the combination of square and cube roots
Sometimes, students confuse the operations involving square and cube roots. For example, \( \sqrt[3]{\sqrt{x^2}} \) needs to be carefully simplified step by step:
- Simplify the inner square root: \( \sqrt{x^2} = |x| \)
- Then apply the cube root: \( \sqrt[3]{|x|} \)
This shows that the operations should not be combined hastily.
Advanced Mathematical Insights
The expression \( \sqrt[3]{x^2} \) often presents challenges and misconceptions in understanding its simplification and properties. Let's delve into a detailed analysis of this expression.
1. Expression Simplification
The cube root of \( x^2 \) can be written as:
\[
\sqrt[3]{x^2} = (x^2)^{\frac{1}{3}}
\]
Applying the power rule \((a^m)^n = a^{m \cdot n}\), we get:
\[
(x^2)^{\frac{1}{3}} = x^{2 \cdot \frac{1}{3}} = x^{\frac{2}{3}}
\]
2. Fractional Exponents and Roots
Understanding fractional exponents is crucial for dealing with expressions involving roots. A fractional exponent represents both a power and a root. For example:
- \(x^{\frac{1}{2}}\) is the square root of \(x\)
- \(x^{\frac{1}{3}}\) is the cube root of \(x\)
- \(x^{\frac{m}{n}}\) represents the \(n\)-th root of \(x^m\)
Therefore, \( x^{\frac{2}{3}} \) can be interpreted as the cube root of \(x^2\).
3. Graphical Representation
The function \( y = \sqrt[3]{x^2} \) behaves differently based on the value of \(x\). It is helpful to plot this function to visualize its behavior. Consider the following points:
- For \( x > 0 \), \( y \) increases as \( x \) increases.
- For \( x < 0 \), \( y \) still increases, but the values remain positive because the cube root of a square is always positive.
The graph is symmetric about the y-axis, illustrating that \( y \) is always positive regardless of whether \( x \) is positive or negative.
4. Properties and Applications
Understanding \( \sqrt[3]{x^2} \) has applications in various fields of mathematics and science:
- Engineering: Used in stress and strain calculations where non-linear scaling is involved.
- Physics: Helps in understanding scaling laws in physical phenomena.
- Computer Science: Useful in algorithms that involve fractional power computations.
5. Misconceptions and Clarifications
Common misconceptions include confusing \( \sqrt[3]{x^2} \) with \( x^{\frac{2}{3}} \) or \( \left( \sqrt{x} \right)^3 \). It is essential to remember the distinction between these expressions and apply the correct rules of exponents and roots.
In summary, \( \sqrt[3]{x^2} \) simplifies to \( x^{\frac{2}{3}} \), and understanding this requires a solid grasp of fractional exponents and their properties. Graphical representations and real-world applications further enhance comprehension and showcase the importance of this mathematical concept.
Practice Problems
To solidify your understanding of the square root of \(x^2\) and related concepts, try solving these practice problems. Use the properties of square roots and the techniques discussed earlier in this guide.
-
Simplify the following expressions:
- \(\sqrt{x^2}\)
- \(\sqrt{9x^2}\)
- \(\sqrt{25x^2}\)
-
Solve the following equations for \(x\):
- \(\sqrt{x^2} = 7\)
- \(\sqrt{4x^2} = 10\)
- \(\sqrt{16x^2} = 32\)
-
Find the values of \(x\) for which the following statements are true:
- \(x^2 = 49\)
- \(9x^2 = 81\)
- \(25x^2 = 225\)
-
Solve these quadratic equations by applying the square root property:
- \(x^2 - 36 = 0\)
- \(4x^2 - 64 = 0\)
- \(9x^2 - 81 = 0\)
-
Evaluate the following expressions for \(x = 5\) and \(x = -5\):
- \(\sqrt{x^2 + 2x + 1}\)
- \(\sqrt{x^2 - 10x + 25}\)
- \(\sqrt{x^2 + 4x + 4}\)
Make sure to check your solutions by substituting back into the original equations where applicable. This will help verify the correctness of your answers.
Summary and Conclusion
In this comprehensive guide, we explored the concept of the square root of x squared and its various mathematical implications. We started by understanding the fundamental properties of square roots and x squared. Here is a summary of the key points:
- The square root of a number is a value that, when multiplied by itself, gives the original number.
- The square root of \(x^2\) is \(|x|\), which accounts for both positive and negative values of x.
- Calculating \(3 \sqrt{x^2}\) involves multiplying the result of \(\sqrt{x^2}\) by 3, which simplifies to \(3|x|\).
We also examined the graphical representation of \(3 \sqrt{x^2}\) and discussed its applications in various real-life scenarios such as physics, engineering, and economics. Additionally, we addressed common misconceptions, including the misunderstanding that \(\sqrt{x^2} = x\) without considering the absolute value.
Advanced mathematical insights were provided to deepen the understanding of the topic, highlighting the importance of absolute values and the behavior of functions involving square roots and squares.
Finally, practice problems were included to reinforce the concepts covered in this guide, ensuring a solid grasp of the subject matter.
In conclusion, understanding the square root of x squared is crucial for solving a wide range of mathematical problems. By mastering the properties and applications of \(\sqrt{x^2}\), students and professionals can enhance their problem-solving skills and apply these principles in various disciplines.
We hope this guide has provided valuable insights and practical knowledge to help you understand and work with the square root of x squared. For further learning, please refer to the additional resources section.

Additional Resources
For those interested in further exploring the topic of square roots, particularly the concept of the cube root of x squared (3√x²), the following resources provide comprehensive explanations, examples, and additional practice problems:
-
Online Math Tutorials
-
Graphing Tools and Calculators
-
Advanced Reading
-
Practice Problems
Video hướng dẫn cách lấy căn bậc ba của x lập phương, hữu ích cho những ai muốn hiểu rõ hơn về căn bậc ba của x bình phương.
Học cách lấy căn bậc ba của x lập phương sử dụng phần tử nhận diện
READ MORE:
Video giải thích chi tiết về căn bậc hai của một số bình phương, hữu ích cho việc hiểu sâu hơn về căn bậc ba của x bình phương.
Căn bậc hai của một số bình phương