What is the Square Root of 208? Learn the Calculation and Methods

The square root of a number is a value that, when multiplied by itself, gives the original number. The square root of 208 can be expressed in several ways:

Exact Value

The exact square root of 208 can be represented as:

\(\sqrt{208}\)

Decimal Approximation

Using a calculator or a numerical method, the square root of 208 is approximately:

\(\sqrt{208} \approx 14.4222\)

Simplified Radical Form

To simplify the square root of 208, we factor it into prime numbers:

208 = 2 × 2 × 2 × 26 = 2³ × 13

Therefore, we can express \(\sqrt{208}\) as:

\(\sqrt{208} = \sqrt{2^3 \times 13} = \sqrt{2^2 \times 2 \times 13} = 2\sqrt{52} = 4\sqrt{13}\)

Step-by-Step Calculation

The step-by-step process to find the square root of 208 involves:

1. Factorize 208 into its prime factors.
2. Identify pairs of prime factors.
3. Take one factor out of each pair and multiply.
4. Multiply the result by the square root of any remaining factors.

For 208:

• Prime factorization: 208 = 2 × 2 × 2 × 26
• Pairs: (2 × 2) = 4
• Remaining factors: 2 and 13

Therefore, \(\sqrt{208} = 4\sqrt{13}\)

Verification

To verify the calculation, we can square the simplified result:

\((4\sqrt{13})^2 = 4^2 \times (\sqrt{13})^2 = 16 \times 13 = 208\)

This confirms that \(\sqrt{208} = 4\sqrt{13}\) is correct.

1. Introduction
2. Definition of Square Root
3. Calculation Methods
• Prime Factorization
• Long Division Method
• Estimation and Refinement
4. Mathematical Approaches
• Algebraic Approach
• Geometric Interpretation
5. Numerical Approximations
• Using a Calculator
• Manual Calculation Steps
6. Historical Significance
• Ancient Civilizations
• Modern Developments
7. Practical Applications
• Engineering
• Physics
• Everyday Life
8. Conclusion

The square root of a number is a value that, when multiplied by itself, gives the original number. In this section, we will explore the square root of 208, its significance, and various ways to understand and calculate it.

The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). For the number 208, the square root is a value which, when squared, equals 208.

Using Mathjax, the square root of 208 can be represented as \( \sqrt{208} \).

Prime Factorization

One way to find the square root of 208 is through prime factorization. The prime factors of 208 are:

\( 208 = 2^4 \times 13 \)

Taking the square root of both sides:

\( \sqrt{208} = \sqrt{2^4 \times 13} = 2^2 \times \sqrt{13} = 4\sqrt{13} \)

Long Division Method

The long division method is a manual technique for finding the square root. It involves a step-by-step process of dividing and averaging to reach the desired precision.

Estimation and Refinement

Estimating and refining involves making an educated guess of the square root, then using that guess to improve accuracy. For instance, since \( 14^2 = 196 \) and \( 15^2 = 225 \), we know that \( \sqrt{208} \) is between 14 and 15.

Algebraic Approach

Using algebra, the square root function can be applied to equations to solve for unknown variables, such as in the quadratic formula.

Geometric Interpretation

Geometrically, the square root of a number can be understood as the side length of a square with an area equal to that number. For 208, it's the side length of a square with an area of 208 square units.

Using a Calculator

Modern calculators provide quick and accurate approximations of square roots. By inputting 208, we find that:

\( \sqrt{208} \approx 14.422 \)

Manual Calculation Steps

Manual steps can involve methods like the Newton-Raphson iteration to approximate square roots to a high degree of accuracy.

Ancient Civilizations

Square roots have been studied since ancient times, with significant contributions from Greek, Indian, and Chinese mathematicians.

Modern Developments

In modern mathematics, the concept of square roots is fundamental to various fields including algebra, calculus, and number theory.

Engineering

Square roots are used in engineering to calculate distances, areas, and in various formulas such as those for stress and strain.

Physics

In physics, square roots appear in equations relating to wave functions, quantum mechanics, and relativity.

Everyday Life

Square roots are useful in everyday problems such as determining the dimensions of a garden, calculating diagonal distances, and in financial calculations.

The square root of 208, like other square roots, has profound implications and applications in various fields of science and daily life. Understanding different methods of calculation and the historical context enriches our appreciation of this mathematical concept.

The square root of 208 is an important mathematical concept with various applications in both theoretical and practical fields. The square root of a number \( n \) is a value that, when multiplied by itself, gives the original number \( n \). For the number 208, its square root is approximately 14.422. This value is derived through different methods such as the prime factorization method, the long division method, and the repeated subtraction method.

One of the primary methods to find the square root of 208 is by using the prime factorization technique. Here, 208 can be expressed as the product of its prime factors: \( 208 = 2 \times 2 \times 2 \times 2 \times 13 \). Simplifying this expression under the square root gives us:

\[\sqrt{208} = \sqrt{2 \times 2 \times 2 \times 2 \times 13} = 2 \times 2 \sqrt{13} = 4\sqrt{13}\]

Thus, the simplified form of the square root of 208 is \( 4\sqrt{13} \), which approximates to 14.422.

Another common approach is the long division method, which involves a step-by-step process to approximate the square root. By pairing the digits and finding the closest squares, we continuously refine our estimate. The result of this method also leads to the approximation:

\[\sqrt{208} \approx 14.422\]

The repeated subtraction method, although less commonly used, involves subtracting successive odd numbers from 208 until the result is zero. This method confirms that 208 is not a perfect square, thus reinforcing that \( \sqrt{208} \) is an irrational number.

Understanding these methods not only helps in computing the square root but also provides insight into the properties and behaviors of numbers. The square root of 208, being an irrational number, has a non-repeating, non-terminating decimal expansion, which is an interesting aspect in the study of number theory.

The square root of a number is a value that, when multiplied by itself, gives the original number. It is often denoted using the radical symbol √. For instance, the square root of 25 is 5 because \(5 \times 5 = 25\). Similarly, we can express the square root of 208 using the radical form: \( \sqrt{208} \).

Mathematically, if \( x \) is the square root of \( y \), then \( x \times x = y \). Therefore, in the case of 208:

\( \sqrt{208} = x \)

\( x \times x = 208 \)

The square root of 208 is not a perfect square, meaning it does not yield a whole number. Instead, it results in an irrational number, which is a non-repeating, non-terminating decimal. The approximate value of the square root of 208 is:

\( \sqrt{208} \approx 14.422 \)

We can simplify the square root of 208 by breaking it down into its prime factors:

\( \sqrt{208} = \sqrt{4 \times 52} = \sqrt{4 \times 4 \times 13} = 4\sqrt{13} \)

In summary:

• The square root of 208 is approximately 14.422.
• It can be expressed in simplified radical form as \( 4\sqrt{13} \).
• Since it is an irrational number, it cannot be exactly represented as a fraction.

Understanding the square root is crucial in various mathematical concepts and applications, including geometry, algebra, and calculus.

Calculating the square root of 208 involves several methods, each with its unique steps and applications. Here are three commonly used methods:

Prime Factorization Method

The prime factorization method involves expressing 208 as a product of its prime factors. Here’s how it works:

• Prime factorize 208: \(208 = 2 \times 2 \times 2 \times 2 \times 13\).
• Group the prime factors into pairs: \( \sqrt{208} = \sqrt{2^4 \times 13} \).
• Simplify the square root: \( \sqrt{208} = \sqrt{(2^2)^2 \times 13} = 2^2 \sqrt{13} = 4\sqrt{13} \).
• Therefore, \( \sqrt{208} \approx 14.422 \).

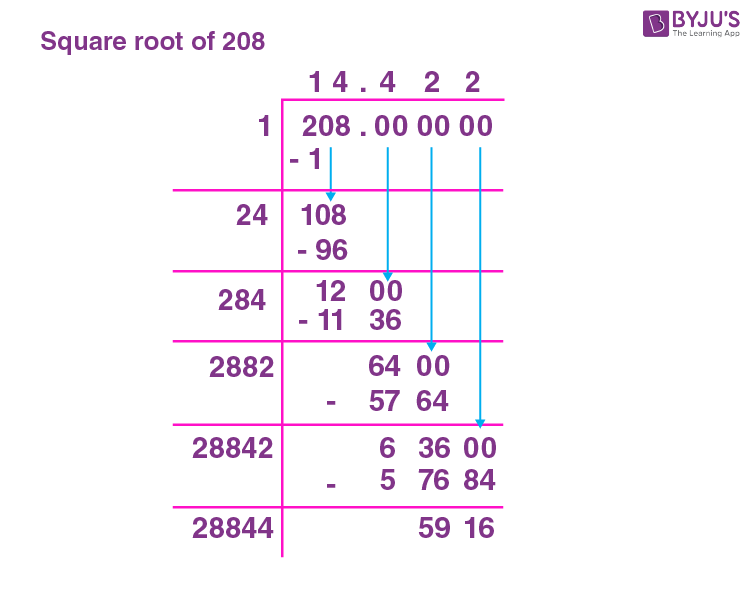
Long Division Method

The long division method is a step-by-step approach to finding the square root of a number. Here’s a detailed procedure:

1. Pair the digits of 208 from right to left: 2 and 08.
2. Find the largest number whose square is less than or equal to 2: This number is 1. Write 1 as the quotient.
3. Subtract the square of the quotient from the leftmost pair (2): \( 2 - 1 = 1 \).
4. Bring down the next pair (08) to get 108.
5. Double the quotient (1) and find the next digit: \( 20 \times 1 = 20 \) (use 1 again as the next digit).
6. Subtract and repeat the process until you reach the desired precision: \( \sqrt{208} \approx 14.422 \).

Repeated Subtraction Method

The repeated subtraction method involves subtracting successive odd numbers from 208 until you reach zero or a negative number. This method is less precise for non-perfect squares but helps understand the concept:

• 208 - 1 = 207
• 207 - 3 = 204
• 204 - 5 = 199
• Continue this process until a negative number is reached.
• Since 208 is not a perfect square, this method will indicate that \( \sqrt{208} \) is an irrational number.

Using these methods, we can determine that the square root of 208 is approximately 14.422. This value is irrational, meaning it cannot be precisely expressed as a simple fraction.

The square root of 208 can be approached through various mathematical methods, each providing a unique perspective on understanding and calculating square roots. Here, we explore some common approaches:

• Prime Factorization:

  One method to find the square root is by breaking down the number into its prime factors. The prime factorization of 208 is:
  \[
  208 = 2^4 \times 13
  \]
  From this factorization, we can simplify the square root as follows:
  \[
  \sqrt{208} = \sqrt{2^4 \times 13} = \sqrt{2^4} \times \sqrt{13} = 4\sqrt{13}
  \]

• Product Rule for Radicals:

  Another approach involves using the product rule for radicals, which states that the square root of a product is the product of the square roots of each factor. For 208:
  \[
  \sqrt{208} = \sqrt{16 \times 13} = \sqrt{16} \times \sqrt{13} = 4 \times \sqrt{13}
  \]

• Decimal Approximation:

  When a precise value is not necessary, a decimal approximation can be useful. Using a calculator, we find:
  \[
  \sqrt{208} \approx 14.4222
  \]
  This approximation is particularly useful for practical applications where an exact radical form is not required.

• Graphical Method:

  The square root can also be estimated graphically by plotting the function \( y = \sqrt{x} \) and finding the value at \( x = 208 \). This visual method helps in understanding the behavior of the square root function.

Each of these methods provides a different insight into the concept of square roots and their calculation, showcasing the versatility and depth of mathematical approaches.

The square root of 208 can be approximated using various numerical methods. Here, we will explore several techniques to find an approximate value for √208:

1. Simple Estimation

To estimate the square root of 208, consider the perfect squares around 208. We know that:

• \(\sqrt{196} = 14\)
• \(\sqrt{225} = 15\)

Since 208 is closer to 196 than to 225, we can estimate that:

\(14 < \sqrt{208} < 15\)

2. Decimal Approximation

Using a calculator, we find that the square root of 208 is approximately:

\(\sqrt{208} \approx 14.4222\)

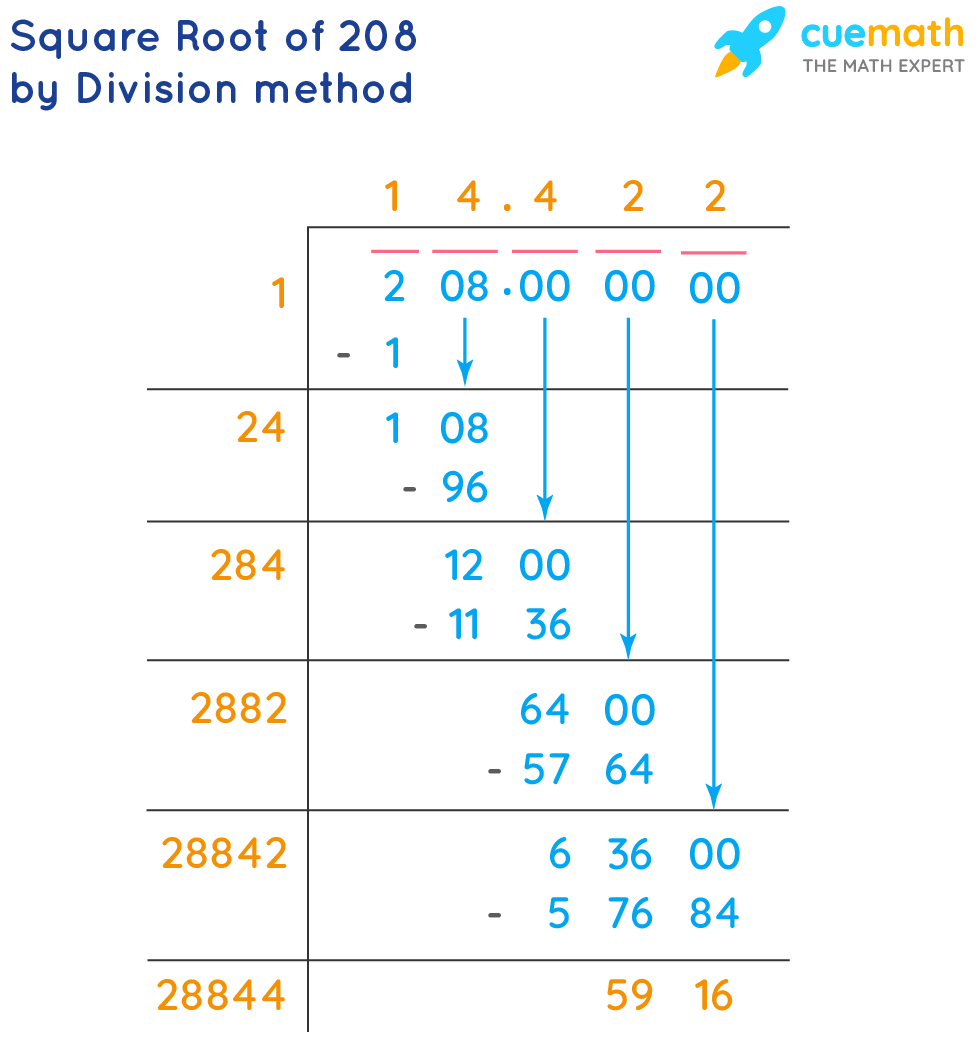
3. Long Division Method

The long division method can be used to find the square root to several decimal places. Here’s a brief outline of the steps:

1. Group the digits in pairs from the decimal point. For 208, this is 2 | 08.
2. Find the largest number whose square is less than or equal to the first pair (2). This number is 1 because \(1^2 = 1\).
3. Subtract 1 from 2, bringing down the next pair (08), to get 108.
4. Double the quotient (1) and use it as the next divisor. Guess the largest digit (X) to append to the divisor and quotient such that \(20X \times X \leq 108\). The digit is 4 because \(204 \times 4 = 816\).
5. Subtract 816 from 1080 (bringing down another pair of zeros) to get 26400.
6. Continue this process to get more decimal places.

4. Newton-Raphson Method

Newton's method provides a way to approximate the roots of a real-valued function. For finding \(\sqrt{208}\), we use:

\( x_{n+1} = \frac{1}{2} \left( x_n + \frac{208}{x_n} \right) \)

Starting with an initial guess \( x_0 = 14 \), we can iterate:

• \( x_1 = \frac{1}{2} \left( 14 + \frac{208}{14} \right) \approx 14.4286 \)
• \( x_2 = \frac{1}{2} \left( 14.4286 + \frac{208}{14.4286} \right) \approx 14.4222 \)

After a few iterations, we converge to the approximate value:

\(\sqrt{208} \approx 14.4222\)

5. Continued Fractions

Another method is using continued fractions. The square root of 208 can be expressed as a continued fraction which provides a way to approximate the value:

\(\sqrt{208} = 14 + \frac{1}{1 + \frac{1}{1 + \frac{1}{2 + \ldots}}}\)

Truncating the continued fraction gives successive approximations:

• \( \sqrt{208} \approx 14 \)
• \( \sqrt{208} \approx 14 + \frac{1}{1} = 15 \)
• \( \sqrt{208} \approx 14 + \frac{1}{1 + \frac{1}{1}} = 14.5 \)

Summary

Using these numerical methods, we find that the square root of 208 is approximately 14.4222. Each method provides a different approach to understanding and approximating the value.

The concept of the square root has deep historical roots, dating back to ancient civilizations. The calculation and understanding of square roots were crucial in the development of mathematics, particularly in solving quadratic equations and understanding geometric properties.

One of the earliest known methods for finding square roots is the "Babylonian method," also known as Heron's method. This iterative approach was used by the ancient Babylonians around 1800 BCE and is remarkably similar to the methods used today.

In ancient Greece, the mathematician Euclid (circa 300 BCE) discussed the properties of square roots in his seminal work, "Elements." Euclid's algorithm for finding the greatest common divisor can be adapted to calculate square roots, showing the interconnectedness of mathematical concepts.

During the Islamic Golden Age (8th to 14th centuries), Persian mathematician Al-Khwarizmi made significant contributions to algebra and introduced methods for solving quadratic equations, which inherently involve finding square roots. His works were later translated into Latin and influenced the development of mathematics in medieval Europe.

By the Renaissance, the understanding and computation of square roots had advanced significantly. The invention of the printing press allowed for wider dissemination of mathematical texts, further spreading knowledge about square roots and other mathematical operations.

In more recent history, the development of calculus by Isaac Newton and Gottfried Wilhelm Leibniz in the 17th century provided new tools for understanding and approximating square roots. The introduction of the decimal system and modern notation also made calculations more accessible and precise.

Overall, the historical development of square roots is a testament to the continuous advancement of mathematical knowledge and its foundational role in various scientific and engineering disciplines.

The square root of 208, approximately 14.42, finds practical applications across various fields. Below are some key examples:

• Engineering and Construction:

  Square roots are critical in calculating lengths of diagonal braces and other angled components to maintain structural integrity. For example, in constructing a right triangle where the legs are 10 units each, the diagonal (hypotenuse) is calculated as \(\sqrt{10^2 + 10^2} = \sqrt{200}\), which is approximately 14.14 units. This principle is used extensively in ensuring buildings and bridges are stable.

• Physics:

  In physics, the square root function is used to compute various quantities like velocity, energy, and force. For instance, the formula for the root mean square velocity of gas particles in a container involves the square root of temperature and molecular mass.

• Finance:

  Square roots are used in calculating stock market volatility, which involves taking the square root of the variance of stock returns. This helps investors assess the risk associated with different investments and make informed decisions.

• Statistics:

  In statistics, the square root is used to calculate standard deviation, which is a measure of the amount of variation or dispersion in a set of values. The standard deviation is the square root of the variance and is crucial for interpreting data distributions.

• Computer Graphics:

  In computer graphics, calculating the distance between points often involves the square root function. For instance, the distance \(D\) between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by \(D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\). This is used in rendering and collision detection in games and simulations.

• Cryptography:

  Square roots play a role in cryptography, particularly in algorithms for digital signatures and public key encryption. These applications ensure secure data transmission and authentication in digital communications.

• Navigation:

  In navigation, the square root is used to calculate distances between points on a map. For example, pilots use the square root formula to determine the shortest flight path between two locations, improving efficiency and safety.

• Telecommunication:

  Square roots are essential in understanding signal strength in wireless communication. The inverse square law, which states that signal strength decreases with the square of the distance from the source, is fundamental in designing efficient communication networks.

The square root of 208, approximately 14.422, is an intriguing number with both theoretical and practical significance. As we have explored, the calculation of this square root can be approached using several methods including prime factorization, long division, and repeated subtraction.

By prime factorization, we discovered that 208 can be expressed as \(208 = 2^4 \times 13\), leading to a simplified radical form of \(4\sqrt{13}\). The long division method provided a step-by-step procedural approach, and the repeated subtraction method highlighted the nature of 208 as a non-perfect square.

Understanding that the square root of 208 is irrational underscores its complexity and the broader category of irrational numbers. These numbers cannot be expressed as simple fractions, adding to their mathematical fascination.

In practical terms, the square root of 208 finds application in various fields such as engineering, physics, and architecture, where precise calculations are essential. Whether used to determine dimensions in construction or to solve complex equations in scientific research, the ability to approximate and understand this square root is invaluable.

In conclusion, the exploration of the square root of 208 reveals both its abstract mathematical beauty and its concrete utility in the real world. This dual nature exemplifies the richness of mathematical study and its relevance to diverse applications.