Topic square root of negative 20: Explore the concept of the square root of negative 20 and its application in mathematics. Learn how imaginary numbers, represented as \( \sqrt{-20} = 2\sqrt{5} \cdot i \), play a crucial role in various theoretical and practical scenarios. Delve into examples and gain insights into the fascinating world of complex numbers.
Table of Content
Square Root of -20
The square root of -20 is expressed using imaginary numbers:
$$\sqrt{-20} = \sqrt{20} \cdot i = 2\sqrt{5} \cdot i$$
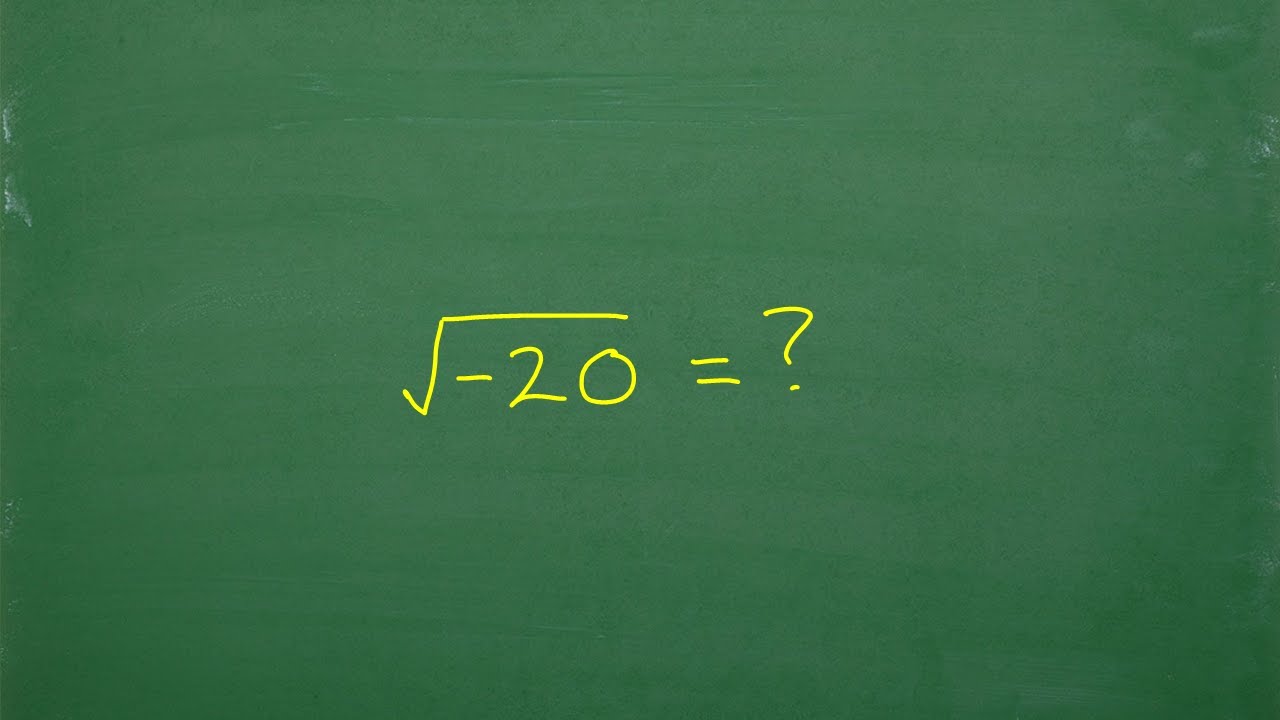
READ MORE:
Introduction
The square root of -20 involves the concept of imaginary numbers, essential in mathematics for dealing with roots of negative values. In this context, the square root of a negative number, such as -20, is expressed as \( \sqrt{-20} = \sqrt{20} \cdot i \), where \( i \) denotes the imaginary unit. This representation extends the number system beyond real numbers, providing solutions to equations that involve negative roots.
Definition of Imaginary Numbers
Imaginary numbers are a class of complex numbers where the real part is zero and the imaginary part is non-zero. They are typically represented as multiples of the imaginary unit \(i\), which is defined as the square root of -1.
To understand imaginary numbers, it is essential to grasp the concept of the imaginary unit \(i\). By definition:
\[ i = \sqrt{-1} \]
Using this definition, any imaginary number can be expressed in the form \(bi\), where \(b\) is a real number. For example, \(5i\) and \(-3i\) are imaginary numbers.
Imaginary numbers extend the real number system to the complex number system, which consists of all possible sums of real numbers and imaginary numbers. A complex number is typically written in the form:
\[ z = a + bi \]
where \(a\) and \(b\) are real numbers. In this form, \(a\) is the real part and \(b\) is the imaginary part of the complex number \(z\).
The introduction of imaginary numbers allows for the solution of equations that do not have real solutions. For example, the equation \(x^2 + 1 = 0\) has no real solution because there is no real number that, when squared, equals -1. However, it has two imaginary solutions:
\[ x = i \text{ and } x = -i \]
Imaginary numbers are useful in various fields, including engineering, physics, and applied mathematics, where they are used to describe phenomena such as oscillations, waveforms, and electrical circuits.
Here are some properties of the imaginary unit \(i\):
- \( i^2 = -1 \)
- \( i^3 = -i \)
- \( i^4 = 1 \)
- The powers of \(i\) repeat every four exponents: \(i, -1, -i, 1\).
In summary, imaginary numbers, represented as multiples of \(i\), are essential components of complex numbers and play a significant role in expanding the number system beyond the real numbers.
Calculation of Square Root of -20
Calculating the square root of a negative number involves using imaginary numbers, denoted by i, where \( i = \sqrt{-1} \).
- First, recognize that the square root of -20 can be expressed as: \[ \sqrt{-20} = \sqrt{20 \cdot -1} \]
- Next, separate the radical into the product of two square roots: \[ \sqrt{-20} = \sqrt{20} \cdot \sqrt{-1} \]
- Since \( \sqrt{-1} = i \): \[ \sqrt{-20} = \sqrt{20} \cdot i \]
- Calculate \( \sqrt{20} \): \[ \sqrt{20} = \sqrt{4 \cdot 5} = \sqrt{4} \cdot \sqrt{5} = 2\sqrt{5} \]
- Combine the results: \[ \sqrt{-20} = 2\sqrt{5} \cdot i \]
Therefore, the square root of -20 is:
\[
\sqrt{-20} = 2\sqrt{5}i
\]
Examples and Applications
Imaginary numbers, particularly those involving the square roots of negative numbers, have several practical applications across various fields. Let's explore some examples and their applications:
- Electrical Engineering: In alternating current (AC) circuit analysis, complex numbers are used to represent impedances. For instance, the impedance of a circuit can be expressed as \( Z = R + iX \), where \( R \) is the resistance and \( X \) is the reactance. Calculations involving \( \sqrt{-1} \) help in understanding phase differences and impedance in AC circuits.
- Signal Processing: Imaginary numbers are crucial in signal processing, particularly in Fourier transforms. The Fourier transform decomposes a function (signal) into its constituent frequencies. The use of \( i = \sqrt{-1} \) allows for the representation and manipulation of these frequency components.
- Quantum Mechanics: In quantum mechanics, complex numbers are essential in describing the state of a system. The wave function, which encapsulates the probabilities of a particle's position and momentum, is a complex-valued function. Imaginary numbers play a key role in the Schrödinger equation, which governs the evolution of these wave functions.
- Control Theory: Control systems often use complex numbers to analyze system stability. The roots of the characteristic equation of a system's differential equation can be complex, and their real and imaginary parts provide information on the system's behavior over time.
- Computer Graphics: Complex numbers are used in computer graphics to perform rotations and transformations. For example, to rotate a point in the complex plane, one can multiply its complex coordinate by another complex number representing the rotation.
Here are some detailed examples to illustrate the calculation and application of the square root of a negative number:
- Example 1: Calculating \( \sqrt{-9} \)
- We know that \( \sqrt{-1} = i \).
- Therefore, \( \sqrt{-9} = \sqrt{9 \cdot (-1)} = \sqrt{9} \cdot \sqrt{-1} = 3i \).
- Example 2: Calculating \( \sqrt{-16} \)
- Similarly, \( \sqrt{-16} = \sqrt{16 \cdot (-1)} = \sqrt{16} \cdot \sqrt{-1} = 4i \).
These examples demonstrate how imaginary numbers, derived from the square roots of negative numbers, are not just theoretical constructs but have significant real-world applications in various scientific and engineering fields.

Conclusion
In this article, we explored the fascinating concept of the square root of -20, diving into the realms of imaginary and complex numbers. Understanding the square root of negative numbers requires a shift from real to complex numbers, where the imaginary unit i plays a crucial role.
We started with the definition of imaginary numbers, establishing that the imaginary unit i is defined as the square root of -1. This foundation allowed us to approach the calculation of the square root of -20.
Through step-by-step calculations, we demonstrated how to simplify √-20 using the properties of imaginary numbers. We expressed -20 as the product of 20 and -1, leading to the result 2√5i.
We also explored examples and applications of imaginary and complex numbers, highlighting their importance in various fields such as engineering, physics, and signal processing. Complex numbers are essential in representing and solving problems involving alternating currents, impedance, and wave functions.
Understanding the square root of negative numbers opens the door to a broader understanding of complex numbers, which have real-world applications in advanced scientific and engineering contexts. By mastering these concepts, you build a strong foundation for further exploration and application of complex mathematical principles.
We encourage you to continue practicing and exploring these concepts to deepen your understanding and confidence. The world of complex numbers is vast and rich with applications, and your journey into this fascinating area of mathematics is just beginning.
Giải Thích Căn Bậc Hai của -20
READ MORE:
Đại Số 2 - Đơn Giản Hóa Căn Bậc Hai để Chuẩn Bị cho Số Ảo, căn(9), căn(20)