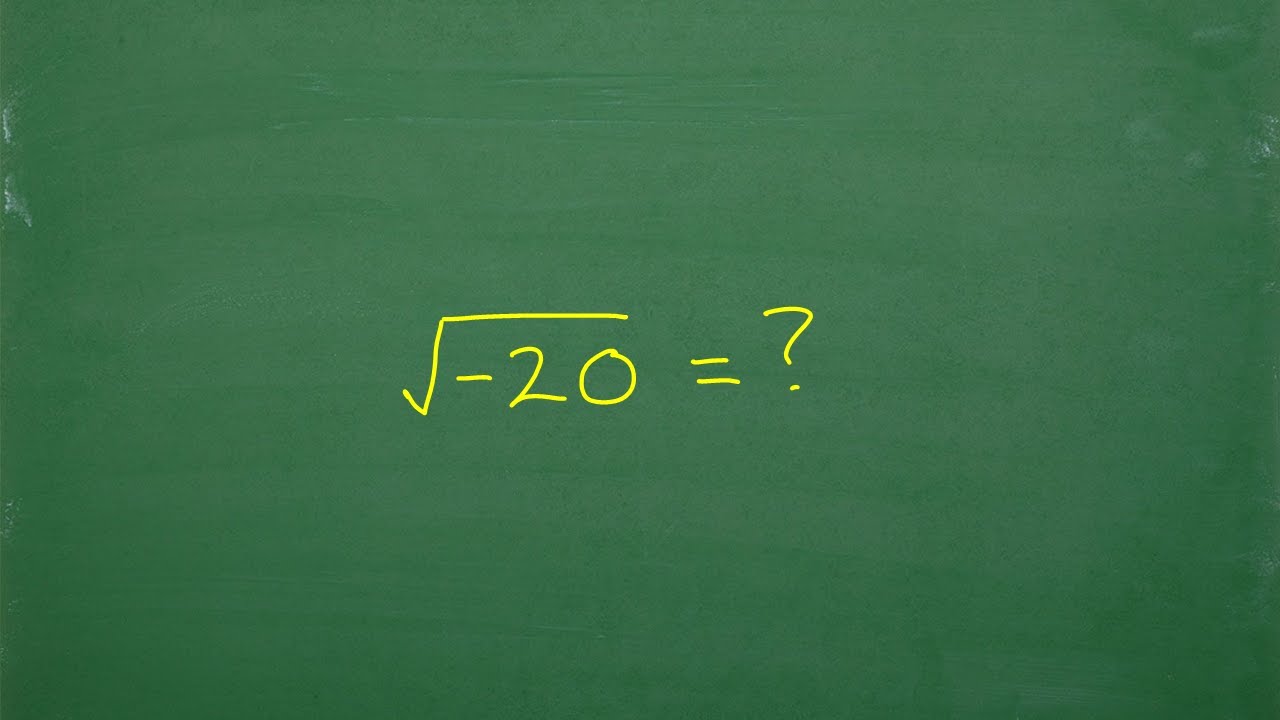Topic squaring square roots: Unlock the secrets of squaring square roots with our comprehensive guide. Learn the fundamental concepts, explore detailed examples, and discover practical applications in algebra and calculus. Whether you're a student or a math enthusiast, this article will help you master the art of simplifying square roots and enhance your mathematical skills.
Table of Content
- Squaring Square Roots
- Introduction to Squaring Square Roots
- Basic Concept of Squaring Square Roots
- Mathematical Representation and Examples
- Properties of Squaring Square Roots
- Applications in Algebra
- Applications in Calculus
- Common Mistakes and Misconceptions
- Advanced Techniques
- Practice Problems and Solutions
- Frequently Asked Questions (FAQ)
- Summary and Conclusion
- YOUTUBE: Xem video để học cách bình phương một đơn thức với dấu căn. Phù hợp cho người học toán và muốn nắm vững các khái niệm về bình phương căn bậc hai.
Squaring Square Roots
The process of squaring square roots involves simplifying expressions that contain square roots by raising them to the power of two. This is an essential concept in algebra that helps in solving equations and simplifying expressions.
Basic Concept
To square a square root, you raise the square root to the power of two. Mathematically, this is represented as:
For example:
This is because the square root and the square are inverse operations.
Examples
Properties
When dealing with variables or more complex expressions, the same rule applies:
Applications
Squaring square roots is useful in solving equations where square roots appear:
- Isolate the square root on one side of the equation:
- Square both sides of the equation to eliminate the square root:
This technique is widely used in algebra and calculus to simplify expressions and solve equations.

READ MORE:
Introduction to Squaring Square Roots
Squaring square roots is a fundamental mathematical operation that simplifies the process of handling square roots in equations and expressions. This technique is crucial for students and professionals in various fields of mathematics and science. Understanding the principles of squaring square roots can help solve complex problems more efficiently.
When you square a square root, you are essentially reversing the operation of taking the square root. The general formula for squaring a square root is:
Here are the steps to understand and perform squaring square roots:
- Identify the square root in the expression.
- Raise the square root to the power of two.
- Simplify the resulting expression to eliminate the square root.
For example, consider the following expression:
When squared, it becomes:
Understanding this process is essential for solving more advanced mathematical problems. In the next sections, we will explore detailed examples, properties, and applications of squaring square roots in algebra and calculus.
Basic Concept of Squaring Square Roots
The concept of squaring square roots involves two fundamental mathematical operations: taking the square root of a number and then squaring that result. These operations are inverse processes, meaning that they cancel each other out when applied consecutively.
To understand this concept, let's break it down step by step:
- Square Root: The square root of a number \( x \) is a value that, when multiplied by itself, gives the original number \( x \). It is denoted by the radical symbol \( \sqrt{} \). For example, the square root of 9 is 3, because \( 3 \times 3 = 9 \). Mathematically, this is represented as \( \sqrt{9} = 3 \).
- Squaring: Squaring a number means multiplying the number by itself. For instance, the square of 3 is \( 3^2 = 9 \).
When you square the square root of a number, you essentially reverse the process of taking the square root, arriving back at the original number. This is represented mathematically as:
\[
(\sqrt{x})^2 = x
\]
For example, if we take the square root of 16, we get 4 because \( \sqrt{16} = 4 \). If we then square this result, we get back to 16 because \( 4^2 = 16 \).
Here is another example with different numbers:
- Find the square root of 25: \( \sqrt{25} = 5 \).
- Square the result: \( 5^2 = 25 \).
Therefore, \( (\sqrt{25})^2 = 25 \).
This principle applies universally, regardless of the number involved, as long as it is a non-negative number, because square roots of negative numbers involve complex numbers (imaginary numbers).
The properties of squaring square roots are foundational in many areas of mathematics, including algebra and calculus, where they are used to simplify expressions and solve equations.
Mathematical Representation and Examples
Squaring a square root is a fundamental concept in mathematics, often seen in various algebraic and geometric contexts. This section explores the process and provides examples to illustrate the principle.
Basic Concept
The square root of a number \( x \), denoted as \( \sqrt{x} \), is a value which, when multiplied by itself, gives \( x \). Mathematically, if \( y = \sqrt{x} \), then \( y^2 = x \).
Squaring a Square Root
When you square a square root, the operations of squaring and square rooting are inverses, and they cancel each other out. This can be represented as:
\( (\sqrt{x})^2 = x \)
For example:
- If \( x = 9 \), then \( \sqrt{9} = 3 \) and \( (\sqrt{9})^2 = 3^2 = 9 \).
- If \( x = 16 \), then \( \sqrt{16} = 4 \) and \( (\sqrt{16})^2 = 4^2 = 16 \).
Examples with Variables
When dealing with variables under the square root, the principle remains the same:
\( (\sqrt{a})^2 = a \)
For example:
- If \( a = x \), then \( (\sqrt{x})^2 = x \).
- If \( a = 4y \), then \( (\sqrt{4y})^2 = 4y \).
Algebraic Expressions
Squaring a square root in algebraic expressions follows the same rules. For instance:
\( (\sqrt{3x + 4})^2 = 3x + 4 \)
This identity can simplify solving equations:
If \( \sqrt{2x + 5} = 3 \), then squaring both sides gives \( 2x + 5 = 9 \).
Complex Numbers
For complex numbers, the concept of squaring a square root extends into imaginary numbers. For example, for a negative number \( x \), say \( -4 \):
\( \sqrt{-4} = 2i \)
Squaring both sides yields:
\( (\sqrt{-4})^2 = (2i)^2 = -4 \)
Square Root of Perfect Squares
Perfect squares are numbers whose square roots are integers. Examples include:
- \( \sqrt{25} = 5 \)
- \( \sqrt{36} = 6 \)
Squaring these square roots reverts them to their original perfect squares:
- \( (\sqrt{25})^2 = 25 \)
- \( (\sqrt{36})^2 = 36 \)
Non-Perfect Squares
For non-perfect squares, squaring the square root still yields the original number. For example:
- \( (\sqrt{2})^2 = 2 \)
- \( (\sqrt{7})^2 = 7 \)
Summary Table
| Expression | Value |
|---|---|
| \( (\sqrt{25})^2 \) | 25 |
| \( (\sqrt{3})^2 \) | 3 |
| \( (\sqrt{-9})^2 \) | -9 |
| \( (\sqrt{a})^2 \) | a |
Understanding the interplay between squaring and square roots is crucial for solving various mathematical problems, from simple arithmetic to complex algebra.
Properties of Squaring Square Roots
Understanding the properties of squaring square roots involves recognizing the fundamental characteristics and mathematical principles that govern these operations. Here are some key properties:
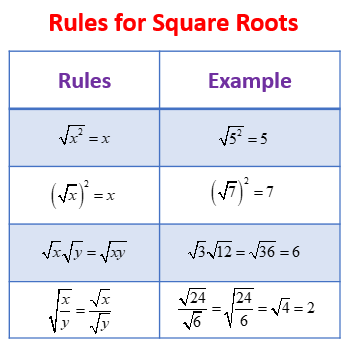
- Square of a Square Root: The square of the square root of a number returns the original number. Mathematically, this is represented as: \[ (\sqrt{x})^2 = x \]
- Commutative Property: Squaring the square root of a number yields the same result as taking the square root of the square of that number. In other words: \[ \sqrt{(x^2)} = x \]
- Positive and Negative Roots: While squaring, both the positive and negative square roots of a number yield the original number. That is: \[ (\sqrt{x})^2 = (\sqrt{-x})^2 = x \]
- Multiplication Property: The square of the product of two numbers is equal to the product of their squares: \[ (\sqrt{x} \times \sqrt{y})^2 = xy \]
- Exponentiation: The square root of a number can be represented as the number raised to the power of 1/2, and squaring this representation returns the number: \[ (\sqrt{x})^2 = (x^{1/2})^2 = x^{1} = x \]
- Even and Odd Properties:
- The square root of an even number is always even, and the square root of an odd number is always odd.
- If a number ends with an even number of zeros, its square root will be an integer.
- If a number ends with an odd number of zeros, its square root will not be a whole number.
- Imaginary Numbers: The square root of a negative number does not exist in the set of real numbers but in the set of complex numbers, represented as: \[ \sqrt{-x} = i\sqrt{x} \] where \( i \) is the imaginary unit.
- Sum of Odd Numbers: The square of a natural number is the sum of the first \( n \) odd numbers. For example: \[ n^2 = 1 + 3 + 5 + \ldots + (2n-1) \]
Examples
Here are some examples to illustrate the properties:
- Example 1: Squaring the square root of 16: \[ (\sqrt{16})^2 = 16 \]
- Example 2: Multiplying and then squaring square roots: \[ (\sqrt{4} \times \sqrt{9})^2 = (2 \times 3)^2 = 6^2 = 36 \]
- Example 3: Square root of a negative number: \[ \sqrt{-25} = 5i \]
Summary
The properties of squaring square roots are fundamental in algebra and calculus, providing a basis for more complex mathematical operations and problem-solving. These properties highlight the consistent and predictable nature of mathematical functions.
Applications in Algebra
Squaring square roots is a fundamental concept in algebra with a variety of applications. Here are some key areas where this concept is utilized:
- Solving Equations:
One of the most common applications is in solving equations involving square roots. For example, to solve an equation like \( \sqrt{x} = 5 \), you would square both sides to eliminate the square root:
\[
(\sqrt{x})^2 = 5^2 \implies x = 25
\] - Quadratic Equations:
Squaring square roots is often used in solving quadratic equations by taking the square root of both sides. For example, for the equation \( x^2 = 16 \), you solve by taking the square root of both sides:
\[
x = \pm \sqrt{16} \implies x = \pm 4
\] - Area and Geometry:
In geometry, squaring square roots is used to find the side length of a square given its area. For instance, if the area \( A \) of a square is known, the side length \( s \) is found by:
\[
s = \sqrt{A}
\]For example, if \( A = 64 \) square units, then:
\[
s = \sqrt{64} = 8 \text{ units}
\] - Solving Radical Equations:
In algebra, radical equations often require squaring both sides to solve for the variable. Consider the equation \( \sqrt{x + 3} = 4 \). Squaring both sides gives:
\[
(\sqrt{x + 3})^2 = 4^2 \implies x + 3 = 16 \implies x = 13
\] - Physics and Engineering:
Square roots are used in various formulas in physics and engineering, such as in calculating the speed of an object under gravity. The time \( t \) for an object to fall from a height \( h \) is given by:
\[
t = \frac{\sqrt{2h}}{g}
\]
In each of these cases, squaring the square root is a crucial step in simplifying the problem and finding the solution.
Applications in Calculus
The concept of squaring square roots finds several important applications in calculus. These applications often involve solving integrals and differential equations where the square root function appears. Here, we will explore some specific scenarios and techniques used in calculus that leverage the properties of squaring square roots.
1. Integration Involving Square Roots
Integrals involving square roots are common in calculus, especially when dealing with certain types of functions and substitutions. One standard method is to use trigonometric substitution to simplify these integrals. For example, consider the integral:
\[
\int \sqrt{x^2 - a^2} \, dx
\]
To solve this, we use the substitution \( x = a \sec(\theta) \). This changes the integral to a form that can be more easily managed:
\[
x = a \sec(\theta), \quad dx = a \sec(\theta) \tan(\theta) \, d\theta
\]
Then, the integral becomes:
\[
\int a \sec(\theta) \tan(\theta) \sqrt{a^2 \sec^2(\theta) - a^2} \, d\theta = \int a^2 \sec(\theta) \tan^2(\theta) \, d\theta
\]
This can be further simplified using trigonometric identities and standard integration techniques.
2. Differential Equations Involving Square Roots
Square roots also appear in the solutions of certain differential equations. For instance, consider a simple differential equation involving a square root:
\[
\frac{dy}{dx} = \sqrt{y}
\]
To solve this, we can separate the variables and integrate both sides:
\[
\int \frac{1}{\sqrt{y}} \, dy = \int dx
\]
This yields:
\[
2\sqrt{y} = x + C
\]
Squaring both sides, we get the solution:
\[
y = \left(\frac{x + C}{2}\right)^2
\]
3. Applications in Arc Length Calculations
The square root function often appears in the formula for arc length of a curve given by \( y = f(x) \). The arc length \( L \) from \( x = a \) to \( x = b \) is given by:
\[
L = \int_a^b \sqrt{1 + \left(\frac{dy}{dx}\right)^2} \, dx
\]
This integral often requires techniques involving squaring the square root and simplifying the integrand.
4. Area Under Curves
Another application is in finding the area under a curve that involves a square root function. For example, finding the area under the curve \( y = \sqrt{x} \) from \( x = 0 \) to \( x = a \) involves the integral:
\[
\int_0^a \sqrt{x} \, dx = \int_0^a x^{1/2} \, dx
\]
Evaluating this integral, we get:
\[
\left[ \frac{2}{3} x^{3/2} \right]_0^a = \frac{2}{3} a^{3/2}
\]
5. Optimization Problems
In optimization problems, functions involving square roots are common. For instance, minimizing the time taken for an object to travel along a path described by a square root function may involve squaring the square root during the process of finding critical points and evaluating second derivatives.
Overall, squaring square roots is a crucial technique in various calculus problems, from integration and differential equations to geometric applications like arc length and area calculations.
Common Mistakes and Misconceptions
Understanding the concept of squaring square roots can sometimes lead to common mistakes and misconceptions. Here are some of the most frequent errors students make and how to avoid them:
- Incorrectly Simplifying Square Roots: One common mistake is assuming that the square root of a sum is the sum of the square roots. For example, many think that \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\), which is incorrect. The correct simplification is \(\sqrt{a + b}\) remains as it is unless specific values of \(a\) and \(b\) allow further simplification.
- Confusing Squaring and Square Roots: Another misconception is that squaring and taking the square root are always interchangeable operations. Remember that \((\sqrt{a})^2 = a\) and \(\sqrt{a^2} = |a|\), not just \(a\). The absolute value is essential to account for both positive and negative values.
- Ignoring Negative Results: When solving equations involving square roots, students often forget that both positive and negative values should be considered. For instance, the equation \(\sqrt{x^2} = x\) should be properly understood as \(\sqrt{x^2} = |x|\), acknowledging that \(x\) can be either positive or negative.
- Mistaking Perfect Squares: Misidentifying non-perfect squares as perfect squares can lead to errors. For example, assuming \(\sqrt{50} = 5\) because \(50\) is close to \(49\), a perfect square. However, the correct simplification is \(\sqrt{50} = 5\sqrt{2}\).
- Errors in Fractional Exponents: Misapplying the rules of exponents when they involve fractions, such as assuming \((a^{1/2})^2 = a^{1/2+2}\). The correct rule is \((a^{1/2})^2 = a^{(1/2) \cdot 2} = a\).
To avoid these common mistakes, it is essential to practice and understand the fundamental properties of square roots and squaring operations. Here's a quick table summarizing the correct and incorrect approaches:
| Incorrect | Correct |
|---|---|
| \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\) | \(\sqrt{a + b}\) |
| \(\sqrt{a^2} = a\) | \(\sqrt{a^2} = |a|\) |
| \(\sqrt{50} = 5\) | \(\sqrt{50} = 5\sqrt{2}\) |
| \((a^{1/2})^2 = a^{1/2+2}\) | \((a^{1/2})^2 = a\) |
By recognizing these misconceptions and applying the correct mathematical principles, you can avoid common pitfalls and strengthen your understanding of squaring square roots.
Advanced Techniques
Squaring square roots may seem straightforward, but there are advanced techniques that can make the process more efficient and provide deeper insights. Here, we explore some of these techniques:
-
Decomposition Method:
This method involves breaking down a number into its prime factors. For instance, to find the square of a square root, we can decompose the number first.
Example:
\(\sqrt{72}\)
- Prime factorize 72: \(72 = 2^3 \cdot 3^2\)
- Take the square root of each factor: \(\sqrt{72} = \sqrt{2^3 \cdot 3^2} = \sqrt{2^3} \cdot \sqrt{3^2} = 2^{3/2} \cdot 3\)
- Simplify: \(2^{3/2} \cdot 3 = 2 \sqrt{2} \cdot 3 = 3 \cdot 2 \sqrt{2} = 6 \sqrt{2}\)
-
Using Algebraic Identities:
Leveraging algebraic identities can simplify complex expressions involving square roots. One such identity is:
\((a+b)^2 = a^2 + 2ab + b^2\)
By substituting square roots into these identities, we can derive simplified results.
Example:
\((\sqrt{a} + \sqrt{b})^2 = a + 2\sqrt{ab} + b\)
-
Iterative Methods for Estimation:
When dealing with non-perfect squares, iterative methods such as Newton's Method can be employed to find more accurate approximations of square roots.
Example:
To find \(\sqrt{N}\):
- Start with an initial guess \(x_0\)
- Use the iteration formula: \(x_{n+1} = \frac{1}{2}\left(x_n + \frac{N}{x_n}\right)\)
- Repeat until the desired precision is achieved.
For instance, to find \(\sqrt{10}\), start with \(x_0 = 3\):
- \(x_1 = \frac{1}{2}\left(3 + \frac{10}{3}\right) = \frac{1}{2}\left(3 + 3.33\right) = 3.165\)
- \(x_2 = \frac{1}{2}\left(3.165 + \frac{10}{3.165}\right) \approx 3.162\)
-
Complex Numbers and Square Roots:
Advanced techniques also extend to complex numbers, where the concept of squaring square roots involves imaginary units.
Example:
The square root of a negative number involves 'i', the imaginary unit: \(\sqrt{-a} = i\sqrt{a}\)
To square it: \((i\sqrt{a})^2 = i^2 \cdot a = -a\)
These advanced techniques not only simplify calculations but also enhance the understanding of the underlying mathematical principles. Practicing these methods can significantly improve problem-solving skills in more complex scenarios.
Practice Problems and Solutions
Practice problems are essential for mastering the concept of squaring square roots. Below are several problems with detailed solutions to help you understand the steps involved.
Problem 1: Basic Square Root
Simplify the following expression:
\(\sqrt{16}\)
Solution:
- Identify the square root of 16, which is a perfect square.
- \(\sqrt{16} = 4\)
Problem 2: Square Root of a Product
Simplify the expression:
\(\sqrt{36 \times 25}\)
Solution:
- Break down the square roots: \(\sqrt{36 \times 25} = \sqrt{36} \times \sqrt{25}\)
- Calculate each square root: \(\sqrt{36} = 6\) and \(\sqrt{25} = 5\)
- Multiply the results: \(6 \times 5 = 30\)
- Thus, \(\sqrt{36 \times 25} = 30\)
Problem 3: Square Root of an Algebraic Expression
Simplify the expression:
\(\sqrt{49x^2}\)
Solution:
- Identify the square root of each component: \(\sqrt{49} = 7\) and \(\sqrt{x^2} = x\)
- Multiply the results: \(7 \times x = 7x\)
- Thus, \(\sqrt{49x^2} = 7x\)
Problem 4: Solving an Equation
Solve for \(x\):
\(\sqrt{x} = 5\)
Solution:
- Square both sides of the equation to eliminate the square root: \((\sqrt{x})^2 = 5^2\)
- This simplifies to: \(x = 25\)
Problem 5: Word Problem
The area of a square is 81 square inches. Find the side length of the square.
Solution:
- Use the formula for the area of a square: \(A = s^2\)
- Given \(A = 81\), solve for \(s\): \(s^2 = 81\)
- Take the square root of both sides: \(s = \sqrt{81}\)
- Since \(\sqrt{81} = 9\), the side length \(s = 9\) inches.
Problem 6: Advanced Algebraic Expression
Simplify the expression:
\(\sqrt{8x^3}\)
Solution:
- Identify the largest square factors: \(8 = 4 \times 2\) and \(x^3 = x^2 \times x\)
- Rewrite the expression: \(\sqrt{8x^3} = \sqrt{4 \times 2 \times x^2 \times x}\)
- Separate the square roots: \(\sqrt{4} \times \sqrt{2} \times \sqrt{x^2} \times \sqrt{x}\)
- Simplify: \(2 \times \sqrt{2} \times x \times \sqrt{x} = 2x\sqrt{2x}\)
- Thus, \(\sqrt{8x^3} = 2x\sqrt{2x}\)
Practice Problems
- Simplify \(\sqrt{49}\)
- Simplify \(\sqrt{100 \times 9}\)
- Simplify \(\sqrt{64y^2}\)
- Solve for \(x\): \(\sqrt{x} = 12\)
- If the area of a square is 144 square centimeters, what is the side length?
Solutions
- \(\sqrt{49} = 7\)
- \(\sqrt{100 \times 9} = \sqrt{100} \times \sqrt{9} = 10 \times 9 = 90\)
- \(\sqrt{64y^2} = 8y\)
- \(\sqrt{x} = 12 \Rightarrow x = 144\)
- Side length = \(\sqrt{144} = 12\) cm
Frequently Asked Questions (FAQ)
Here are some common questions and detailed answers about squaring square roots:
-
Q: What happens when you square a square root?
A: When you square a square root, you get the original number. This is because squaring and taking the square root are inverse operations. Mathematically, \( (\sqrt{x})^2 = x \).
-
Q: What is the difference between a square and a square root?
A: A square is the result of multiplying a number by itself, denoted as \( n^2 \). A square root is a number that, when multiplied by itself, gives the original number, denoted as \( \sqrt{n} \). For example, \( 3^2 = 9 \) and \( \sqrt{9} = 3 \).
-
Q: How do you solve a square-root equation?
A: To solve a square-root equation, isolate the square root on one side and then square both sides of the equation to eliminate the square root. For example, to solve \( \sqrt{x} = 5 \), square both sides to get \( x = 25 \).
-
Q: What are extraneous solutions, and how do you identify them?
A: Extraneous solutions are solutions derived from an equation that do not satisfy the original equation. These often arise when squaring both sides of an equation. Always substitute the solutions back into the original equation to verify their validity.
-
Q: What does it mean to rationalize the denominator?
A: Rationalizing the denominator involves eliminating any square roots in the denominator of a fraction. For instance, to rationalize \( \frac{1}{\sqrt{2}} \), multiply both the numerator and the denominator by \( \sqrt{2} \) to get \( \frac{\sqrt{2}}{2} \).
-
Q: How are square roots used in the real world?
A: Square roots are used in various real-world applications, including calculating areas, in engineering to determine dimensions and tolerances, in physics for solving equations involving speed and distance, and in statistics for standard deviation and normal distribution calculations.
Summary and Conclusion
The process of squaring square roots involves understanding both squaring and square rooting as fundamental mathematical operations. Here’s a comprehensive summary of the key points:
- Basic Definitions:
- Square Root: The square root of a number \(a\) is a value \(b\) such that \(b^2 = a\). This can be denoted as \(\sqrt{a}\).
- Squaring: Squaring a number means multiplying it by itself, i.e., \(a^2 = a \times a\).
- Mathematical Properties:
- Principal Square Root: The principal square root of a non-negative number is its non-negative root. For example, \(\sqrt{25} = 5\), not \(-5\).
- Squaring a Square Root: When you square a square root, you get the original number, i.e., \((\sqrt{a})^2 = a\).
- Applications:
- Algebra: Squaring and square roots are fundamental in solving quadratic equations and understanding polynomial roots.
- Calculus: These operations are crucial in derivatives and integrals involving root functions and in solving differential equations.
- Common Mistakes:
- Confusing the principal square root with the negative square root.
- Incorrectly assuming \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) for negative values.
- Advanced Techniques:
- Using prime factorization to find square roots of larger numbers.
- Applying long division methods for precise calculation of square roots.
In conclusion, understanding the relationship between squaring and square roots is essential for various mathematical applications. Mastering these concepts enables solving more complex problems in algebra and calculus, and helps avoid common pitfalls associated with these operations. Continuous practice and application of these principles will enhance proficiency and confidence in handling mathematical challenges involving square roots and their squares.
Xem video để học cách bình phương một đơn thức với dấu căn. Phù hợp cho người học toán và muốn nắm vững các khái niệm về bình phương căn bậc hai.
Bình phương một đơn thức với dấu căn
READ MORE:
Khám phá cách bình phương các căn bậc hai trong toán học với những ví dụ minh họa dễ hiểu và thú vị.
Bình Phương Các Căn Bậc Hai