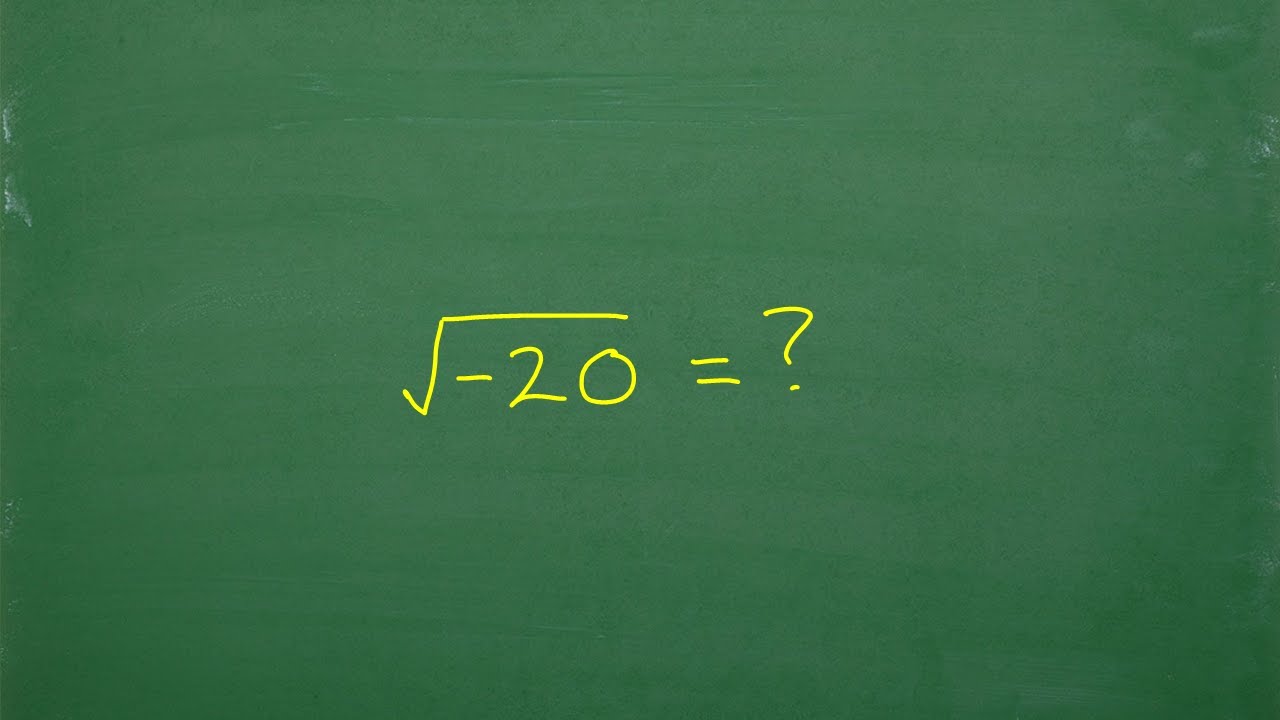Topic square root 2 x square root 2: Discover the fundamentals of multiplying square roots of 2 in this comprehensive guide. Learn how to calculate and apply this mathematical operation with ease. Explore practical examples and gain insights into its significance in various mathematical contexts.
Table of Content
Square Root of 2 Times Square Root of 2
In mathematics, when you multiply the square root of 2 by itself, denoted as \( \sqrt{2} \times \sqrt{2} \), the result simplifies as follows:
\[ \sqrt{2} \times \sqrt{2} = 2 \]
This is because multiplying a number by itself is equivalent to squaring the number.
Therefore, the product of \( \sqrt{2} \) and \( \sqrt{2} \) is \( 2 \).
READ MORE:
Understanding the Basics
When dealing with the expression "square root 2 x square root 2," it's essential to grasp the fundamental concepts of square roots and their multiplication:
- Square Root Definition: The square root of a number \( x \), denoted as \( \sqrt{x} \), is a value that, when multiplied by itself, gives \( x \).
- Square Root of 2: \( \sqrt{2} \) is an irrational number approximately equal to 1.414.
- Multiplication of Square Roots: When multiplying square roots, such as \( \sqrt{2} \times \sqrt{2} \), you multiply the numbers inside the square root: \( \sqrt{2} \times \sqrt{2} = \sqrt{2 \times 2} = \sqrt{4} = 2 \).
- Result Interpretation: The result \( 2 \) indicates that the square root of 2 multiplied by itself equals 2, reinforcing the basic property of square roots.
Properties of Square Roots
Square roots have several important properties that are fundamental to understanding their behavior in mathematics. Here, we will discuss some key properties and illustrate them with examples, especially focusing on √2.
1. Product of Square Roots
One of the essential properties is that the product of the square roots of two numbers is equal to the square root of the product of those two numbers:
\[
\sqrt{a} \times \sqrt{b} = \sqrt{a \times b}
\]
For example:
\[
\sqrt{2} \times \sqrt{2} = \sqrt{2 \times 2} = \sqrt{4} = 2
\]
2. Simplifying Square Roots
Square roots can often be simplified if the number under the square root is a perfect square or can be factored into perfect squares. For instance:
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- \(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\)
3. Square Root of a Product
We have already seen that \(\sqrt{a} \times \sqrt{b} = \sqrt{a \times b}\). Let's see another example:
\[
\sqrt{3} \times \sqrt{12} = \sqrt{3 \times 12} = \sqrt{36} = 6
\]
4. Rationalizing Denominators
When a square root appears in the denominator of a fraction, it is often desirable to rationalize the denominator. This involves multiplying the numerator and the denominator by a suitable square root to eliminate the square root in the denominator. For example:
\[
\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]
5. Properties Involving Addition and Subtraction
Unlike multiplication, the square root of a sum or difference is not simply the sum or difference of the square roots. For instance:
- \(\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}\)
- \(\sqrt{a - b} \neq \sqrt{a} - \sqrt{b}\)
However, you can often simplify expressions involving square roots using other algebraic techniques.
6. Special Values
Some square roots have special values that are often used in mathematical problems. These include:
- \(\sqrt{1} = 1\)
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- \(\sqrt{16} = 4\)
- \(\sqrt{25} = 5\)
7. Square Root Function
The square root function, \(f(x) = \sqrt{x}\), is defined for non-negative real numbers. It is a fundamental function in mathematics with the following properties:
- Domain: \(x \geq 0\)
- Range: \(y \geq 0\)
- The graph of \(f(x) = \sqrt{x}\) is a curve that increases slowly as \(x\) increases.
Understanding these properties of square roots is crucial for solving various mathematical problems and for simplifying expressions involving square roots.
Calculation Methods
Calculating the product of square roots can be done using several methods. Here, we will explore different techniques to calculate \(\sqrt{2} \times \sqrt{2}\) in a detailed and step-by-step manner.
1. Direct Multiplication
The most straightforward method is to use the property of square roots that states:
\[
\sqrt{a} \times \sqrt{b} = \sqrt{a \times b}
\]
Applying this to our specific example:
\[
\sqrt{2} \times \sqrt{2} = \sqrt{2 \times 2} = \sqrt{4} = 2
\]
2. Using Exponents
Square roots can also be expressed using fractional exponents. This method involves the following steps:
- Express the square root as an exponent: \(\sqrt{2} = 2^{1/2}\)
- Multiply the exponents: \(2^{1/2} \times 2^{1/2} = 2^{(1/2 + 1/2)} = 2^1\)
- Simplify the result: \(2^1 = 2\)
3. Numerical Approximation
In cases where an exact value might be less intuitive or when dealing with irrational numbers, numerical approximation can be used:
- Approximate \(\sqrt{2} \approx 1.414\)
- Multiply the approximations: \(1.414 \times 1.414 \approx 2\)
4. Visual Method
For visual learners, understanding the multiplication of square roots can be reinforced using geometric interpretation:
Consider a square with side length \(\sqrt{2}\). The area of the square can be calculated as:
\[
\text{Area} = \sqrt{2} \times \sqrt{2} = 2
\]
This geometric visualization confirms that the product \(\sqrt{2} \times \sqrt{2}\) indeed equals 2.
5. Verification by Squaring
Another method to verify the result is by squaring the product of the square roots:
- Calculate the product: \(x = \sqrt{2} \times \sqrt{2}\)
- Square both sides: \(x^2 = (\sqrt{2} \times \sqrt{2})^2\)
- Since \((\sqrt{2} \times \sqrt{2})^2 = 2\): \(x^2 = 2\)
- Take the square root of both sides to solve for \(x\): \(x = \sqrt{2}\)
Thus, confirming that \(\sqrt{2} \times \sqrt{2} = 2\).
Summary
All these methods demonstrate that the product of \(\sqrt{2} \times \sqrt{2}\) consistently results in 2. Understanding and applying these various calculation techniques can help reinforce the fundamental properties of square roots and their operations.
Applications in Mathematics
Understanding how the multiplication of square roots, such as , is applied in various mathematical contexts is crucial for both theoretical and practical purposes. Here are some notable applications:
1. Simplifying Radical Expressions
One of the fundamental applications of multiplying square roots is in simplifying radical expressions. By understanding that , students can simplify complex radical expressions more efficiently.
2. Geometry and Area Calculations
In geometry, square roots are often used to determine the lengths of sides when the area is known. For instance, the area (A) of a square is related to the length of its sides (s) by the formula . If the area of a square is 4 square units, then each side is units.
3. Solving Quadratic Equations
Square roots are essential in solving quadratic equations using the quadratic formula, where solutions are given by . Here, the term under the square root determines the nature of the solutions.
4. Physics and Engineering
In physics, square roots are used in formulas involving gravitational force, kinematics, and energy. For example, the time (t) it takes for an object to fall from a height (h) under gravity is given by . This application shows the direct use of square roots in calculating time from a given height.
5. Real-World Problem Solving
Square roots are used in various real-world scenarios such as determining speeds from skid marks in accident investigations or calculating side lengths in construction projects. For example, if the skid marks are d feet long, the speed (v) of the car can be approximated by .
6. Trigonometry
In trigonometry, square roots appear in the Pythagorean theorem and in the calculation of distances in coordinate geometry. For instance, the distance between two points is given by .
Conclusion
The multiplication of square roots, such as , is not just a fundamental mathematical operation but also a powerful tool applied across various fields. Its applications range from simplifying expressions to solving real-world problems, highlighting its importance in both theoretical and practical mathematics.

Practical Examples and Exercises
Understanding the multiplication of square roots can be enhanced through practical examples and exercises. Here, we provide a variety of problems to solidify your comprehension of
Example 1: Simplifying Square Roots
Simplify the following expression:
- \(\sqrt{2} \times \sqrt{2}\)
Solution:
Using the property of square roots, \(\sqrt{a} \times \sqrt{a} = a\), we find:
Example 2: Applying the Product Rule
Simplify \(\sqrt{8} \times \sqrt{2}\).
- \(\sqrt{8} \times \sqrt{2} = \sqrt{8 \times 2}\)
- \(\sqrt{16} = 4\)
Exercise 1: Simplify Square Roots
- Simplify \(\sqrt{50} \times \sqrt{2}\)
- Simplify \(\sqrt{18} \times \sqrt{2}\)
Exercise 2: Solve Equations Involving Square Roots
Find the value of \(x\) in the following equation:
Solution:
- Square both sides: \((\sqrt{2x + 3})^2 = 10^2\)
- Result: \(2x + 3 = 100\)
- Simplify: \(2x = 97\)
- Divide: \(x = \frac{97}{2} = 48.5\)
Table of Square Roots
| Number | Square Root |
|---|---|
| 2 | \(\sqrt{2} \approx 1.414\) |
| 8 | \(\sqrt{8} \approx 2.828\) |
| 16 | \(\sqrt{16} = 4\) |
| 50 | \(\sqrt{50} \approx 7.071\) |
| 18 | \(\sqrt{18} \approx 4.243\) |
Exercise 3: More Simplification Problems
- Simplify \(\sqrt{75} \times \sqrt{3}\)
- Simplify \(\sqrt{200} \times \sqrt{2}\)
These exercises and examples help in understanding the multiplication and simplification of square roots, reinforcing the mathematical concepts with practical application.
Conclusion
Understanding the calculation of \( \sqrt{2} \times \sqrt{2} \) offers valuable insights into the properties and applications of square roots. This exploration highlights a fundamental principle: the product of two square roots of the same number equals the original number.
For instance, \( \sqrt{2} \times \sqrt{2} = \sqrt{4} = 2 \). This principle can be extended to other square roots, providing a consistent method for simplifying expressions and solving equations.
In mathematics, the properties of square roots are utilized in various domains, including algebra, geometry, and calculus. They play a crucial role in solving quadratic equations, simplifying complex expressions, and understanding the behavior of functions.
The practical examples and exercises covered in this guide demonstrate the versatility of square roots in mathematical problem-solving. Whether rationalizing denominators, completing the square, or evaluating roots of negative numbers, the ability to manipulate and simplify square roots is a fundamental skill.
By mastering these concepts, students and mathematicians alike can deepen their understanding of mathematical relationships and enhance their problem-solving capabilities. This foundational knowledge paves the way for more advanced studies and applications in various fields of science, engineering, and beyond.
In conclusion, the exploration of \( \sqrt{2} \times \sqrt{2} \) is more than a simple calculation; it is a gateway to appreciating the elegance and power of mathematical principles that underpin much of the mathematical world.
READ MORE:
Khám phá video 'Căn Bậc Hai của 2' và tìm hiểu các ứng dụng và tính chất của căn bậc hai trong toán học.
Căn Bậc Hai của 2