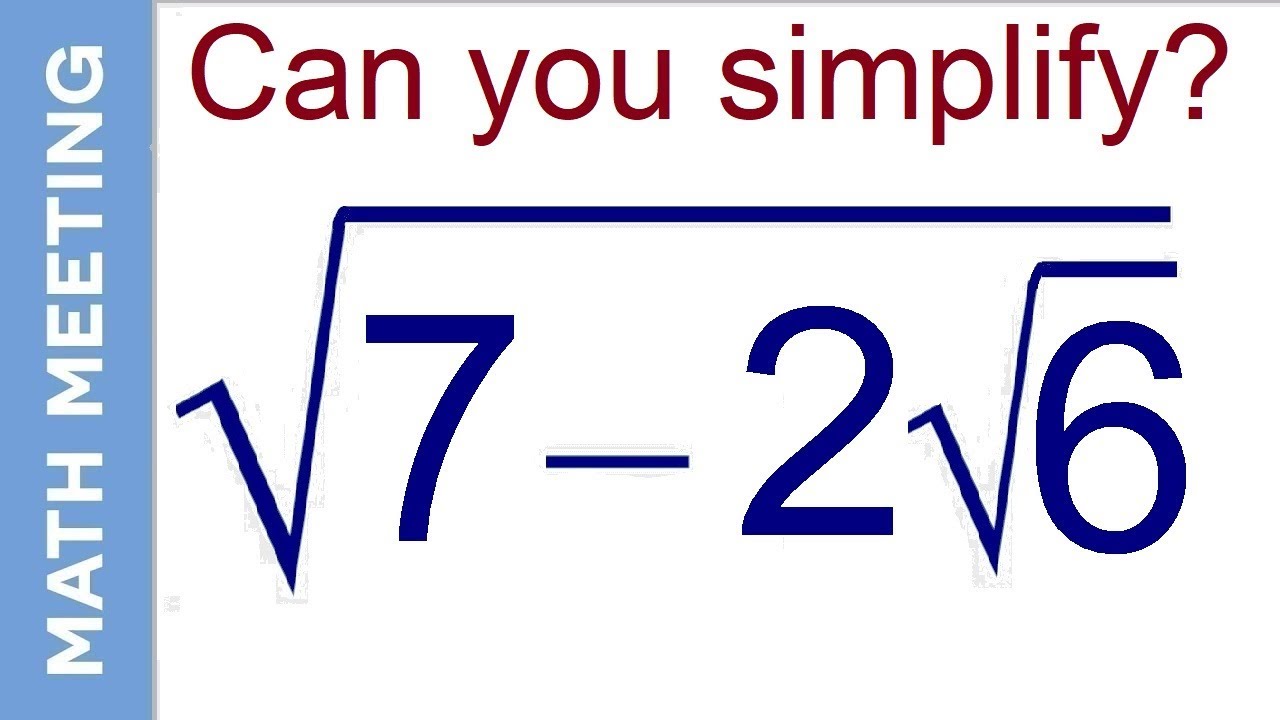4 Root 2 Squared: Understanding and Simplifying the Expression

When squaring the expression \( (4\sqrt{2})^2 \), we need to apply the rules of exponents and radicals. Here is a step-by-step guide:

Step-by-Step Simplification

1. Start with the expression: \( (4\sqrt{2})^2 \)
2. Use the property of exponents: \( (a \cdot b)^2 = a^2 \cdot b^2 \)
3. Apply this property: \( (4\sqrt{2})^2 = 4^2 \cdot (\sqrt{2})^2 \)
4. Simplify each part:
   • \( 4^2 = 16 \)
   • \( (\sqrt{2})^2 = 2 \)
5. Multiply the results: \( 16 \cdot 2 = 32 \)

Therefore, the simplified form of \( (4\sqrt{2})^2 \) is \( 32 \).

Mathematical Explanation Using MathJax

To further understand this, we can use MathJax to display the mathematical process:

\[ (4\sqrt{2})^2 = 4^2 \cdot (\sqrt{2})^2 = 16 \cdot 2 = 32 \]

General Property of Squaring a Product

This example demonstrates a general property of squaring a product of a constant and a square root:

\[ (a\sqrt{b})^2 = a^2 \cdot b \]

Where \( a \) is any real number and \( b \) is a non-negative number.

Conclusion

Understanding the properties of exponents and radicals allows us to simplify expressions like \( (4\sqrt{2})^2 \) efficiently. This process is crucial in algebra and higher-level mathematics.

Square roots and exponents are fundamental concepts in mathematics that form the basis for many advanced topics. Understanding these concepts is crucial for solving various mathematical problems and for applications in science and engineering.

Square Roots:

• The square root of a number x, denoted as \( \sqrt{x} \), is a value that, when multiplied by itself, gives the number x.
• For example, \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \).
• Square roots can also be expressed using fractional exponents: \( \sqrt{x} = x^{1/2} \).
• Negative numbers do not have real square roots since a negative number times itself is always positive. However, complex numbers can have square roots.

Exponents:

• An exponent indicates how many times a number, called the base, is multiplied by itself. For instance, in \( 3^2 \), 3 is the base and 2 is the exponent, meaning \( 3 \times 3 \).
• Exponents are written as superscripts. The expression \( a^n \) means that the base a is raised to the power of n.
• Common rules of exponents include:
  • Product Rule: \( a^m \times a^n = a^{m+n} \)
  • Quotient Rule: \( \frac{a^m}{a^n} = a^{m-n} \)
  • Power Rule: \( (a^m)^n = a^{mn} \)
  • Zero Exponent: \( a^0 = 1 \) (where a ≠ 0)
  • Negative Exponent: \( a^{-n} = \frac{1}{a^n} \)

In the context of square roots and exponents, understanding the relationship between these two concepts is vital. For example, squaring a square root, as in \( (\sqrt{4})^2 \), simplifies back to the original number, in this case, 4. Similarly, taking the square root of a squared number, \( \sqrt{(4^2)} \), also returns to the original base, which is 4.

Squaring a number is a fundamental mathematical operation that involves multiplying a number by itself. This operation is denoted using the exponent 2, as in \( a^2 \), where \( a \) is the base.

Here is a step-by-step explanation of squaring:

1. Definition:
   • Squaring a number means raising it to the power of 2.
   • The result of squaring a number \( a \) is \( a^2 \).
   • For example, squaring 3 gives \( 3^2 = 9 \).
2. Mathematical Notation:
   • The notation \( a^2 \) is read as "a squared" and represents \( a \times a \).
   • In general, if \( a \) is any real number, \( a^2 = a \times a \).
3. Properties of Squaring:
   • Squaring a positive number results in a positive number.
   • Squaring a negative number results in a positive number. For example, \( (-3)^2 = 9 \).
   • Squaring zero results in zero: \( 0^2 = 0 \).
4. Squaring Square Roots:
   • When a square root is squared, the result is the original number inside the square root.
   • For example, \( (\sqrt{2})^2 = 2 \).
   • This is because \( \sqrt{2} \times \sqrt{2} = 2 \).
5. Example of Squaring a Number with a Square Root:
   • Consider the expression \( (4\sqrt{2})^2 \).
   • Using the property of exponents, we can expand this as:

     \[
     (4\sqrt{2})^2 = 4^2 \times (\sqrt{2})^2
     \]

   • Calculating each part:

     \[
     4^2 = 16
     \]

     \[
     (\sqrt{2})^2 = 2
     \]

   • Therefore:

     \[
     (4\sqrt{2})^2 = 16 \times 2 = 32
     \]

Understanding the concept of squaring is essential for solving problems involving exponents, polynomials, and algebraic expressions. It is also a building block for more advanced mathematical topics.

The expression \( (4\sqrt{2})^2 \) can be simplified by following these steps:

1. Identify the Components:
   • The expression consists of the number 4 and the square root of 2, which are multiplied together.
   • To square this expression, we need to square both components.
2. Rewrite the Expression:
   • Using the property of exponents, we can rewrite the expression:

     \[
     (4\sqrt{2})^2 = 4^2 \times (\sqrt{2})^2
     \]

3. Square Each Component:
   • Square the number 4:

     \[
     4^2 = 16
     \]

   • Square the square root of 2:

     \[
     (\sqrt{2})^2 = 2
     \]

4. Multiply the Results:
   • Multiply the results of the squaring operations:

     \[
     16 \times 2 = 32
     \]

5. Final Simplified Form:
   • Thus, the simplified result of the expression \( (4\sqrt{2})^2 \) is:

     \[
     (4\sqrt{2})^2 = 32
     \]

This step-by-step process shows how to simplify the expression \( (4\sqrt{2})^2 \) by squaring each part and then combining the results. This method can be used for other similar expressions involving multiplication and square roots.

To solve the expression (4√2)², we can apply mathematical rules and properties related to exponents and square roots.

1. Understand the Expression:

   The given expression is (4√2)². This means we need to square both the numerical part (4) and the square root part (√2).

2. Apply the Square to Each Part:

   We can rewrite the expression as:

   (4√2)² = (4²) × (√2)²

3. Calculate Each Component:
   • Square the Numerical Part:

     4² = 16

   • Square the Square Root Part:

     (√2)² = 2

4. Combine the Results:

   Now, multiply the results from the two components:

   16 × 2 = 32

Thus, (4√2)² = 32.

Properties Used:

• Exponentiation and Square Roots:

  When you square a square root, the result is the number under the square root. For example, (√a)² = a.

• Multiplication of Exponents:

  When multiplying terms with exponents, you apply the exponent to each part of the term separately, then combine the results.

Common Mistakes to Avoid:

• Not Squaring Each Component Separately:

  Ensure to square both the numerical and the square root parts individually before combining them.

• Incorrectly Handling Square Roots:

  Remember that squaring a square root eliminates the square root, leaving the base number.

When calculating \((4\sqrt{2})^2\), it's easy to make some common mistakes. Being aware of these errors can help improve your accuracy and mathematical skills.

• Misinterpreting the Order of Operations: Always follow the correct order of operations. First, handle the square root, then the multiplication, and finally the squaring. Incorrectly sequencing these steps can lead to errors.

  Correct Calculation:

  1. Compute the square root: \(\sqrt{2}\)
  2. Multiply by 4: \(4 \cdot \sqrt{2}\)
  3. Square the result: \((4\sqrt{2})^2\)

• Incorrect Squaring of a Product: Remember, squaring the product of numbers is different from squaring each number separately. For \((4\sqrt{2})^2\), you must square the entire product, not individually.

  Correct Formula:

  \[(4\sqrt{2})^2 = 4^2 \cdot (\sqrt{2})^2 = 16 \cdot 2 = 32\]

• Approximating Too Early: The square root of 2 is an irrational number. Avoid rounding it off too early in your calculations, as this can lead to significant inaccuracies.

  Tip: Keep your calculations in exact form as long as possible before approximating the final result.

• Forgetting Parentheses: Ensure that you use parentheses correctly to indicate the operations. This helps in maintaining the intended order of calculations and avoids errors, especially when dealing with complex expressions.

  Example:

  Correct: \((4\sqrt{2})^2\)

  Incorrect: \(4 \sqrt{2}^2\)

• Ignoring Mathematical Conventions: Follow standard mathematical conventions such as the precedence of operations. Disregarding these rules can lead to incorrect results.

By being aware of these common mistakes and practicing careful and accurate methods, you can significantly improve your mathematical proficiency.

Understanding how to work with square roots and exponents is essential in various fields such as physics, engineering, and computer science. Here, we will explore practical examples and applications of squaring the expression \(4\sqrt{2}\).

Example 1: Simplifying the Expression \((4\sqrt{2})^2\)

1. First, recall the mathematical property that \((a\sqrt{b})^2 = a^2 \cdot b\).
2. In this case, \(a = 4\) and \(b = 2\).
3. Calculate \(a^2\): \(4^2 = 16\).
4. Multiply the result by \(b\): \(16 \cdot 2 = 32\).
5. Thus, \((4\sqrt{2})^2 = 32\).

Example 2: Applying in a Physics Problem

Consider a scenario where you need to calculate the kinetic energy (KE) of an object with mass \(m\) moving at velocity \(v = 4\sqrt{2}\) m/s. The formula for kinetic energy is:

\(KE = \frac{1}{2}mv^2\)

1. Substitute \(v = 4\sqrt{2}\) into the formula: \(KE = \frac{1}{2}m(4\sqrt{2})^2\).
2. Simplify the expression inside the parentheses: \((4\sqrt{2})^2 = 32\).
3. Now the formula is \(KE = \frac{1}{2}m \cdot 32\).
4. Simplify further: \(KE = 16m\).
5. Hence, the kinetic energy is \(16m\) joules, where \(m\) is the mass of the object in kilograms.

Example 3: Using in Engineering Calculations

In electrical engineering, consider a scenario where you need to find the power \(P\) dissipated in a resistor with resistance \(R\) when the current \(I = 4\sqrt{2}\) amperes flows through it. The power formula is:

\(P = I^2R\)

1. Substitute \(I = 4\sqrt{2}\) into the formula: \(P = (4\sqrt{2})^2R\).
2. Simplify the expression: \((4\sqrt{2})^2 = 32\).
3. Now the formula is \(P = 32R\).
4. Thus, the power dissipated is \(32R\) watts, where \(R\) is the resistance in ohms.

Practical Tip

When dealing with square roots and exponents in real-life applications, always ensure to simplify the expressions step-by-step to avoid errors. The property \((a\sqrt{b})^2 = a^2 \cdot b\) is particularly useful and can simplify many calculations quickly.

Squaring radicals can sometimes be confusing, especially with terms involving roots and exponents. Here are some frequently asked questions to help clarify the process:

• What does it mean to square a radical?

  Squaring a radical means multiplying the radical by itself. For example, \((\sqrt{a})^2 = a\). This process removes the square root, resulting in the original number under the radical.

• What is the square of \(4\sqrt{2}\)?

  To find the square of \(4\sqrt{2}\), you multiply the expression by itself:

  \[
  (4\sqrt{2})^2 = 4^2 \cdot (\sqrt{2})^2 = 16 \cdot 2 = 32
  \]

• Are there any common mistakes to avoid when squaring radicals?

  Yes, a common mistake is forgetting to square both the coefficient and the radical separately. For example, with \(3\sqrt{5}\), you should compute \( (3\sqrt{5})^2 \) as follows:

  \[
  (3\sqrt{5})^2 = 3^2 \cdot (\sqrt{5})^2 = 9 \cdot 5 = 45
  \]

• Can negative numbers be squared inside radicals?

  Yes, but it’s important to remember that squaring a negative number results in a positive number. For example:

  \[
  (-\sqrt{a})^2 = (\sqrt{a})^2 = a
  \]

  This holds true because the square of any real number is always non-negative.

• What happens if you square an imaginary number under a radical?

  Squaring an imaginary number involves using \(i\), where \(i = \sqrt{-1}\). For example:

  \[
  (\sqrt{-4})^2 = (\sqrt{-1 \cdot 4})^2 = (\sqrt{-1} \cdot \sqrt{4})^2 = (2i)^2 = 4i^2 = 4(-1) = -4
  \]

  This shows that squaring an imaginary number results in a negative real number.

• What is the principal square root?

  The principal square root is the non-negative root of a number. For example, the principal square root of 25 is 5, even though -5 is also a square root of 25. The symbol \(\sqrt{}\) typically represents the principal square root.

For those looking to delve deeper into the topic of squaring radicals and square roots, the following resources offer comprehensive explanations and additional practice problems:

• This video series explains the fundamentals of square roots and provides step-by-step instructions on how to calculate them. It also covers the relationship between squares and square roots.

• An extensive guide that explains what square roots are, how to calculate them, and their properties. It also includes interactive elements and practical examples to aid learning.

• This resource provides detailed explanations of square roots and exponents, including rules and properties. It also features example problems and practice exercises.

• An article that covers the mathematical concept of square roots, including historical context and practical applications. It is a great resource for those interested in the theoretical background.

• This educational resource explains square roots in the context of rational numbers and provides examples to illustrate key concepts. It is ideal for pre-algebra students.

These resources should help you gain a deeper understanding of square roots and their applications, offering both theoretical knowledge and practical problem-solving techniques.