Topic what is the square root of 2000: Discover the intriguing world of mathematics as we explore the square root of 2000, a key concept bridging theory and practical application, from basic calculations to advanced mathematical theorems and real-world examples.
Table of Content
What is the square root of 2000?
To find the square root of 2000, we can simplify it by factoring out perfect squares. Starting with 2000, we can see that 2000 = 400 * 5.
Now, we can write the square root of 2000 as the square root of (400 * 5).
Using the property that the square root of a product is the product of the square roots of the factors, we can rewrite it as the square root of 400 times the square root of 5.
The square root of 400 is a perfect square, which is 20. Therefore, the square root of 2000 is equal to 20 times the square root of 5.
Thus, the simplified form of the square root of 2000 is 20√5.
READ MORE:
Definition and Value
The square root of a number is a value that, when multiplied by itself, gives the original number. In the case of 2000, the square root is denoted as √2000, representing a number that squared equals 2000. This concept is fundamental in both algebra and geometry, offering insights into various mathematical and real-world problems.
To find the value of √2000, we use numerical methods or a calculator, as the square root of 2000 is not a whole number. The precise value of √2000 is approximately 44.7214. This number, though irrational, plays a crucial role in calculations and theoretical math, providing a bridge to understanding complex mathematical concepts and their applications.
Understanding the square root of 2000 also involves familiarity with the properties of square roots in general, such as:
- The square root of a number can be positive or negative since both squared will give the original positive number.
- Square roots of non-perfect squares are irrational numbers, meaning they cannot be expressed as a simple fraction.
- The square root function is crucial in solving quadratic equations, which appear in various scientific and engineering contexts.
Thus, the square root of 2000 is more than just a number; it\"s a gateway to deeper mathematical exploration and understanding.

Calculation Methods
Calculating the square root of 2000 can be approached through several methods, each with its unique steps and applications. Here, we explore the most common techniques used to find √2000, suitable for different levels of mathematical proficiency.
- Using a Calculator: The simplest method is to use a scientific calculator. Entering 2000 and pressing the square root function (√) will instantly give you the result, approximately 44.7214.
- Estimation: Start by identifying the perfect squares closest to 2000, which are 44^2=1936 and 45^2=2025. Since 2000 is closer to 2025, you can estimate that √2000 is slightly less than 45.
- Prime Factorization: Break down 2000 into its prime factors (2^4 * 5^3) and take the square root of each factor. This method simplifies the original square root calculation but requires familiarity with prime numbers.
- Newton\"s Method: An iterative numerical method that starts with an initial guess and refines it using the formula xₙ₊₁ = 1/2(xₙ + 2000/xₙ). This method is more complex but highly effective for precise calculations.
- Babylonian Method: Also known as the Hero\"s method, it is similar to Newton\"s method and involves making an initial guess followed by iterative adjustments to get closer to the actual square root value.
Each of these methods offers a different path to understanding and calculating the square root of 2000, from simple estimations to more sophisticated numerical techniques. Depending on the context and required precision, the choice of method can vary, highlighting the rich variety of tools available in mathematics for solving seemingly straightforward problems.

Applications and Examples
The square root of 2000, while a specific mathematical concept, finds relevance in various practical, educational, and professional scenarios. Understanding its applications helps bridge the gap between abstract mathematics and real-world problems.
- Geometry: In geometry, calculating the area of squares and rectangles often involves square roots. For example, if the area of a square is 2000 square units, finding one side of the square requires computing the square root of 2000, approximately 44.7214 units.
- Physics: Square roots play a crucial role in physics, particularly in formulas involving speed, velocity, and other rates of change. For instance, in determining the intensity of a physical quantity that spreads out in a spherical manner from a point source, the inverse square law is applied, which often requires the use of square roots.
- Statistics and Probability: The standard deviation, a fundamental concept in statistics, involves the square root in its calculation. Understanding the dispersion or spread of a set of values around their mean in datasets approximating or exceeding 2000 elements can involve square root computations.
- Engineering: Engineers often use square roots when calculating resistances, forces, and energies, especially in fields like structural, electrical, and mechanical engineering. The square root of 2000 could represent specific thresholds or parameters within these calculations.
- Finance: In finance, the square root is used in the computation of compound interest, volatility measures, and in the assessment of risk and return in investment portfolios. For example, understanding the volatility of an asset might involve calculations that include the square root of 2000 or similar values.
These examples illustrate the broad utility of the square root of 2000 across disciplines, underscoring the importance of mathematical concepts in analyzing and solving complex problems in both theoretical and practical contexts.
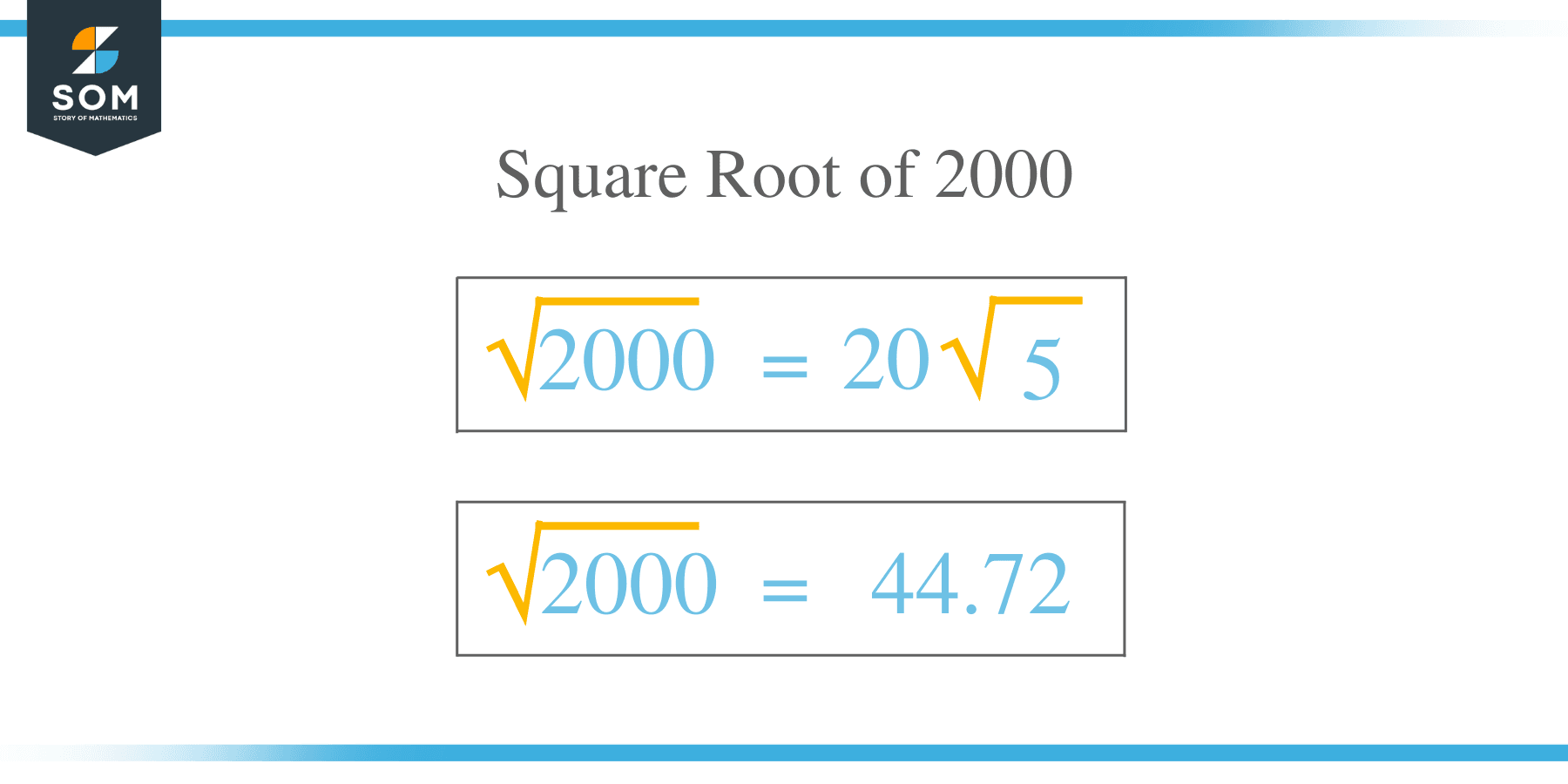
Tools and Calculators
Calculating the square root of 2000 is made accessible by a variety of tools and calculators, each designed to fit different needs and levels of complexity. Whether you are a student, educator, or professional, these resources can provide accurate results efficiently.
- Scientific Calculators: Most scientific calculators have a square root function, allowing for quick calculations. Simply enter 2000 and press the square root button to get the result.
- Online Calculators: There are numerous free online calculators specifically designed for square root calculations. These tools often provide step-by-step solutions, making them ideal for educational purposes.
- Math Software: Programs like MATLAB, Mathematica, and Python (with libraries such as NumPy) offer powerful functions for calculating square roots and are widely used in engineering and scientific research.
- Mobile Apps: Several mobile applications are available that not only calculate square roots but also offer tutorials and practice problems to help understand the concept better.
- Spreadsheets: Spreadsheet software like Microsoft Excel and Google Sheets can calculate square roots using built-in functions. For example, entering \"=SQRT(2000)\" will yield the square root of 2000.
These tools and calculators simplify complex calculations and enhance learning and problem-solving skills by providing quick and accurate results for the square root of 2000 and other mathematical operations.

_HOOK_
Mathematical Concepts and Theorems
Understanding the square root of 2000 opens the door to various mathematical concepts and theorems that are foundational to both pure and applied mathematics. These principles not only explain the properties of square roots but also their significance in broader mathematical contexts.
- Square Root Principle: This principle states that for any positive number x, there exists a positive number y such that y² = x. This concept is pivotal in solving quadratic equations and in understanding the geometric interpretation of numbers.
- Pythagorean Theorem: A cornerstone of geometry, the Pythagorean theorem, relates the lengths of the sides of a right triangle. The square root plays a critical role in calculating the length of a side when the lengths of the other two are known.
- Irrational Numbers: The square root of 2000 is an irrational number, which means it cannot be exactly expressed as a fraction of two integers. The concept of irrational numbers is vital in understanding the continuum of real numbers.
- Limit and Continuity: The calculation of square roots can be approached through the concept of limits, especially in the context of Newton\"s method. This ties into the broader mathematical concepts of limit and continuity, fundamental in calculus.
- Algebraic Identities: Square roots are involved in various algebraic identities and formulas, such as the binomial theorem and the difference of squares, which are used to simplify expressions and solve equations.
These concepts and theorems illustrate the depth and breadth of mathematical knowledge connected to the square root of 2000, showcasing its importance beyond a mere number and highlighting its role in the vast universe of mathematics.
Embark on a fascinating journey through mathematics with the square root of 2000, where theory meets application, enriching our understanding of the world through the elegance and complexity of numbers.

Find the square root of 2000 without a calculator
\"Unravel the mystery of the square root with this captivating video! Watch as complex mathematical concepts are simplified and discover the beauty hidden within numbers. Enhance your math skills and uncover the secrets of the square root today!\"
READ MORE:
Solve sqrt(2000) + sqrt(500) | Math Olympiads | A nice square root question
\"Enter the thrilling world of Math Olympiads with this incredible video! Journey alongside the brightest minds as they battle it out in intense competitions, showcasing their exceptional problem-solving abilities. Be inspired and take your own mathematical abilities to new heights by watching this riveting Math Olympiads video!\"