Topic what is the square root of 202: Curious about the square root of 202? In this article, we explore the value and significance of this mathematical concept. Learn how to calculate it, its applications, and why it's important in various fields. Join us on a journey to understand the square root of 202 and enhance your math knowledge!
Table of Content
- Square Root of 202
- Introduction to Square Roots
- Definition and Basic Concepts
- Mathematical Background of Square Roots
- How to Calculate the Square Root of 202
- Methods for Finding Square Roots
- Approximation Techniques for Square Roots
- Using a Calculator to Find Square Roots
- Manual Calculation Methods
- Prime Factorization Method
- Long Division Method
- Properties of Square Roots
- Real-World Applications of Square Roots
- Scientific Uses of Square Roots
- Square Roots in Engineering
- Square Roots in Daily Life
- Conclusion
- YOUTUBE: SQUARE ROOT OF 202
Square Root of 202
The square root of 202 is approximately \( \sqrt{202} \approx 14.2127 \).

READ MORE:
Introduction to Square Roots
Square roots are fundamental mathematical concepts that allow us to determine a number which, when multiplied by itself, gives the original number. For example, the square root of 202 is a number that, when squared, equals 202. Mathematically, this is represented as:
\[\sqrt{202}\]
In general, the square root of a number \( x \) is written as:
\[\sqrt{x}\]
Here are some important properties and steps to understand square roots:
- Definition: The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \).
- Notation: The square root of \( x \) is denoted as \(\sqrt{x}\).
- Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. For example, the square roots of 202 are \(\sqrt{202}\) and \(-\sqrt{202}\).
- Perfect Squares: A number is a perfect square if its square root is an integer. For instance, 16 is a perfect square because \(\sqrt{16} = 4\).
Calculating the square root of a number can be done using various methods, including estimation, prime factorization, and using a calculator. Below is a step-by-step outline of these methods:
- Estimation: Find two perfect squares between which the number lies. For 202, it lies between 196 (\(14^2\)) and 225 (\(15^2\)). Thus, \(\sqrt{202}\) is between 14 and 15.
- Prime Factorization: Break down the number into its prime factors and simplify. However, for 202, which is not a perfect square, this method is less straightforward.
- Using a Calculator: The most accurate way to find the square root of 202 is by using a scientific calculator, which gives approximately \(\sqrt{202} \approx 14.21\).
Understanding square roots is crucial in various fields such as algebra, geometry, engineering, and physics, where they are used to solve equations, determine distances, and more.
Definition and Basic Concepts
The square root of a number is a value which, when multiplied by itself, gives the original number. In mathematical notation, the square root of a number \( x \) is denoted as \( \sqrt{x} \). For example, the square root of 202 can be expressed as \( \sqrt{202} \).
The square root of 202 is an irrational number, meaning it cannot be expressed as a simple fraction. The approximate decimal form of the square root of 202 is:
\[
\sqrt{202} \approx 14.2127
\]
To understand the concept of square roots more thoroughly, consider the following properties and methods:
- Radicand: The number under the radical sign. For \( \sqrt{202} \), 202 is the radicand.
- Perfect Squares: Numbers whose square roots are integers. For example, 16 is a perfect square because \( \sqrt{16} = 4 \). However, 202 is not a perfect square.
- Principal Square Root: The non-negative square root of a number. In our case, the principal square root of 202 is approximately 14.2127.
Square roots can be found using various methods, including:
- Using a Calculator: Most calculators have a square root function, usually represented as \( \sqrt{x} \). Entering 202 and pressing this function key will yield approximately 14.2127.
- Long Division Method: A manual method involving setting up the number in pairs of digits and finding the largest possible digit at each step to construct the square root. This method is less common with the availability of calculators.
The square root can also be expressed using exponents. The square root of 202 can be written as:
\[
\sqrt{202} = 202^{1/2}
\]
Understanding the square root concept is fundamental in various fields, including mathematics, engineering, and science, where it is often necessary to solve quadratic equations, analyze periodic functions, and more.
Mathematical Background of Square Roots
The concept of square roots is foundational in mathematics, deeply intertwined with the operations of squaring and radicals. To understand square roots, we start with the idea of squaring a number, which involves multiplying the number by itself. For example, \(5 \times 5 = 25\), so the square of 5 is 25. Conversely, the square root of a number is a value that, when multiplied by itself, yields the original number. For instance, the square root of 25 is 5, denoted as \(\sqrt{25} = 5\).
Square roots have several key properties:
- Principal Square Root: This refers to the non-negative square root of a number. For example, while both 5 and -5 are square roots of 25, \(\sqrt{25}\) typically refers to the positive root, 5.
- Negative Square Roots: Every positive number has two square roots: one positive and one negative. Therefore, \(\sqrt{25} = \pm5\).
- Zero: Zero is the only number that has exactly one square root, which is zero itself, \(\sqrt{0} = 0\).
The process of finding square roots can vary based on the nature of the number:
- Perfect Squares: These are numbers like 1, 4, 9, 16, etc., which are squares of integers. Their square roots are exact integers. For example, \(\sqrt{16} = 4\).
- Non-Perfect Squares: Numbers that are not perfect squares have irrational square roots. For example, \(\sqrt{2}\) is approximately 1.414 and continues indefinitely without repeating.
To calculate square roots, several methods can be used:
- Using a Calculator: The most straightforward way to find a square root is by using a calculator. For instance, \(\sqrt{202}\) can be found directly by pressing the square root button on a calculator.
- Manual Methods: Techniques such as the long division method or iterative methods like the one developed by Heron of Alexandria can be used for manual calculation. These methods involve making an initial guess and refining it through iterations to get closer to the actual square root.
Understanding square roots is not only crucial for solving mathematical problems but also for applications in various fields such as engineering, physics, and statistics, where they are used to describe relationships and patterns within data.
How to Calculate the Square Root of 202
Calculating the square root of 202 can be approached in several ways, including using a calculator, approximation techniques, and manual calculation methods. Below, we will detail these methods step-by-step.
Using a Calculator
One of the simplest methods is to use a calculator:
- Turn on the calculator.
- Enter the number 202.
- Press the square root (√) button.
- The display will show the square root of 202, which is approximately 14.2127.
Approximation Techniques
If you don't have a calculator, you can estimate the square root of 202 by finding the two perfect squares it lies between:
- 142 = 196
- 152 = 225
Since 202 is closer to 196, you can start with 14.2 and refine your estimate:
- Calculate 14.22 = 201.64
- This is very close to 202, so the square root of 202 is approximately 14.2.
Manual Calculation Methods
There are also manual methods like the Long Division Method:
Long Division Method
- Start with a guess (e.g., 14) and divide 202 by this guess: 202 / 14 ≈ 14.4286.
- Averaging 14 and 14.4286 gives a better approximation: (14 + 14.4286) / 2 ≈ 14.2143.
- Repeat the process with the new estimate: 202 / 14.2143 ≈ 14.2124.
- Averaging again: (14.2143 + 14.2124) / 2 ≈ 14.2133.
- Continue iterating until the desired precision is achieved. The square root of 202 is approximately 14.2127.
Prime Factorization Method
The Prime Factorization Method is less straightforward for 202, as it is not a perfect square. For completeness, 202 can be factored into primes:
- 202 = 2 × 101
Since these factors don't pair, this method confirms that 202 isn't a perfect square and manual or calculator methods are preferable for finding its square root.
By following these methods, you can accurately determine the square root of 202, whether you use a calculator, estimation techniques, or manual calculations.

Methods for Finding Square Roots
There are several methods to find the square root of a number like 202:
- Estimation Method: By approximation, we can estimate that the square root of 202 is approximately between 14 and 15.
- Prime Factorization Method: Breaking down 202 into its prime factors (2 and 101) allows us to find the square root manually.
- Long Division Method: This method involves a step-by-step division process to find the square root of 202 with precision.
- Newton's Method: A numerical approximation method that iteratively improves estimates using calculus.
Approximation Techniques for Square Roots
When finding the square root of 202, approximation techniques can be helpful:
- Digit-by-Digit Method: A sequential approach to approximate each digit of the square root of 202.
- Newton's Method: Iterative method using calculus to refine the estimate of the square root of 202.
- Binomial Expansion: Using the first few terms of the binomial series to estimate the square root of 202.
- Using Logarithms: Utilizing properties of logarithms to estimate the square root of 202.
Using a Calculator to Find Square Roots
Calculating the square root of 202 using a calculator is straightforward:
- Enter the number 202 into the calculator.
- Press the square root (√) button or use the appropriate function on the calculator.
- Obtain the result, which should be approximately 14.2126.
Manual Calculation Methods
Manual methods for calculating the square root of 202 include:
- Prime Factorization Method: Breaking down 202 into prime factors (2 and 101) and using properties of exponents.
- Long Division Method: Step-by-step division process to find the square root of 202 with precision.

Prime Factorization Method
The prime factorization method for finding the square root of 202 involves these steps:
- Identify the prime factors of 202, which are 2 and 101.
- Group the prime factors into pairs: \( \sqrt{202} = \sqrt{2 \times 101} \).
- Take the square root of each pair: \( \sqrt{2 \times 101} = \sqrt{2} \times \sqrt{101} \).
- Calculate the square roots individually: \( \sqrt{2} \approx 1.414 \) and \( \sqrt{101} \approx 10.05 \).
- Multiply the results: \( \sqrt{202} \approx 1.414 \times 10.05 \approx 14.177 \).
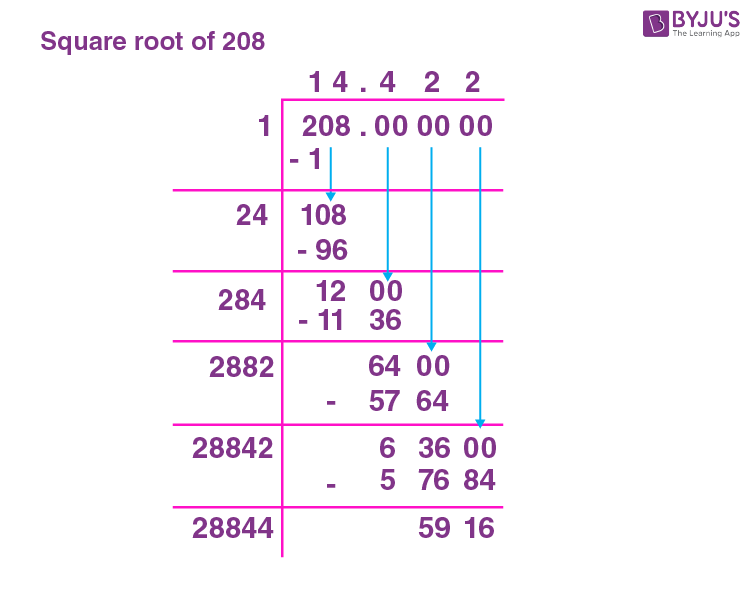
Long Division Method
The long division method is a manual way to find the square root of a number. Here, we will calculate the square root of 202 step by step using this method.
- Set up 202 in pairs of digits from right to left and add one set of 00 because we want to find a decimal value:
2 | 02 | 00
- Starting with the first set (2):
The largest perfect square less than or equal to 2 is 1, and the square root of 1 is 1. Write 1 above the line and 1 below the 2.
1 1 2 -1 1 - Calculate 2 - 1 = 1 and bring down the next pair of digits (02):
1 1 02 -1 1 - Double the current quotient (1), which gives us 2, and write it below:
1 1 02 2_ -1 1 Find a digit (X) such that 2X * X is less than or equal to 102. The digit X here is 4, since 24 * 4 = 96.
- Place 4 in the quotient and subtract 96 from 102:
1 4 1 02 24 * 4 -96 6 - Bring down the next pair of digits (00) to make it 600. Double the quotient (14) and write it below:
1 4 1 02 24 * 4 -96 6 28_ Find a digit (Y) such that 280Y * Y is less than or equal to 600. The digit Y here is 2, since 282 * 2 = 564.
- Place 2 in the quotient and subtract 564 from 600:
1 4 2 1 02 24 * 4 -96 6 280 * 2 -564 36 - The quotient so far is 14.2, and you can continue this process to get more decimal places as needed.
Therefore, the approximate value of the square root of 202 using the long division method is 14.2.
Properties of Square Roots
The square root is a unique mathematical operation with several interesting properties. Understanding these properties is essential for mastering various mathematical concepts. Here are some of the key properties of square roots:
- Non-negative Output: The principal square root of a non-negative number is always non-negative. For example, \(\sqrt{25} = 5\) and not \(-5\).
- Square of a Square Root: The square of the square root of a number returns the original number. Mathematically, \( (\sqrt{a})^2 = a \). For example, \( (\sqrt{9})^2 = 9 \).
- Product Property: The square root of a product is equal to the product of the square roots of the factors. This can be expressed as: \[ \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \] where \(a \geq 0\) and \(b \geq 0\).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and denominator. This property is represented as: \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \] where \(b \neq 0\).
- Even and Odd Properties: The square root of an even perfect square is always even, and the square root of an odd perfect square is always odd. For example, \(\sqrt{144} = 12\) (even) and \(\sqrt{225} = 15\) (odd).
- Irrationality: If a number is not a perfect square, its square root is irrational. For example, \(\sqrt{2}\) and \(\sqrt{3}\) are irrational numbers.
- Imaginary Numbers: The square root of a negative number is imaginary. This is denoted using the imaginary unit \(i\), where \(i = \sqrt{-1}\). For example, \(\sqrt{-9} = 3i\).
- Perfect Square Property: The square root of a perfect square is always an integer. For example, \(\sqrt{49} = 7\).
Understanding these properties allows for a deeper comprehension of algebraic manipulations and problem-solving techniques involving square roots.
Real-World Applications of Square Roots
Square roots have numerous practical applications in various fields. Here are some key areas where square roots are essential:
- Engineering: In engineering, square roots are used to determine the natural frequency of structures like bridges and buildings. This helps engineers predict how structures will react to different loads, such as wind or traffic, and ensure their stability and safety.
- Finance: In finance, square roots are used to calculate stock market volatility. By taking the square root of the return variance, investors can assess the risk of an investment. This helps in making informed decisions about buying or selling stocks.
- Architecture: Architects use square roots to determine distances and design elements accurately. For example, the Pythagorean theorem, which involves square roots, is crucial in calculating the length of the sides of right-angled triangles in various architectural designs.
- Physics: In physics, square roots are used in formulas to calculate velocities, accelerations, and other dynamic properties of objects. This is essential for understanding the motion and interaction of physical bodies.
- Statistics: Square roots are used in statistics to calculate standard deviation, a measure of how spread out numbers are in a data set. The standard deviation is the square root of the variance and is crucial for data analysis and interpretation.
- Computer Science: In computer science, square roots are used in algorithms for encryption, image processing, and graphics. For instance, encryption algorithms use square roots to generate secure keys for data protection.
- Navigation: Square roots are used in navigation to calculate the shortest distance between two points. This is essential for pilots, sailors, and hikers to determine the most efficient routes.
- Telecommunications: In telecommunications, the signal strength decreases with the square of the distance from the transmitter, known as the inverse square law. This principle helps in designing efficient communication systems.
- Photography: In photography, the aperture of a camera lens is related to the square root of the f-number. This relationship helps photographers control the amount of light entering the camera to achieve the desired exposure.
Overall, square roots are fundamental in solving real-world problems across diverse disciplines, making them a crucial mathematical tool.

Scientific Uses of Square Roots
Square roots play a crucial role in various scientific disciplines, facilitating calculations and understanding phenomena that involve quadratic relationships or measurements of magnitude.
- Physics: In physics, square roots are used extensively in equations involving energy, such as the calculation of potential energy in gravitational systems or the determination of wave amplitudes in electromagnetic waves.
- Engineering: Engineers utilize square roots in structural analysis to assess forces acting on materials or components, determining safe load capacities and stress distributions in bridges, buildings, and machinery.
- Statistics: In statistical analysis, square roots are employed to calculate standard deviations, which measure the amount of variation or dispersion in a set of data points.
- Computer Science: Algorithms in computer science often require square roots for tasks like numerical methods, optimization techniques, and cryptography where prime factorization methods depend on efficient square root calculations.
Overall, square roots are a fundamental mathematical tool across scientific fields, enabling precise calculations and enhancing understanding of complex phenomena.
Square Roots in Engineering
Square roots play a crucial role in various engineering fields, providing essential tools for solving problems related to design, analysis, and construction. Here are some key applications of square roots in engineering:
1. Structural Engineering
In structural engineering, square roots are used to calculate the natural frequencies of structures. The natural frequency is crucial for ensuring that a building or bridge does not resonate with external vibrations, which could lead to structural failure. The formula involves the square root of the stiffness to mass ratio:
\[ f = \frac{1}{2\pi} \sqrt{\frac{k}{m}} \]
where \( f \) is the natural frequency, \( k \) is the stiffness, and \( m \) is the mass of the structure.
2. Electrical Engineering
In electrical engineering, square roots are used in the calculation of root mean square (RMS) values of alternating current (AC) voltages and currents. RMS values are essential for determining the effective power in AC circuits:
\[ V_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} v^2(t) \, dt} \]
where \( V_{RMS} \) is the root mean square voltage, \( T \) is the period, and \( v(t) \) is the instantaneous voltage.
3. Mechanical Engineering
In mechanical engineering, the square root is used to determine the velocity of an object in free fall. This is derived from the kinematic equation for distance traveled under constant acceleration:
\[ v = \sqrt{2gh} \]
where \( v \) is the final velocity, \( g \) is the acceleration due to gravity, and \( h \) is the height from which the object falls.
4. Civil Engineering
Square roots are essential in civil engineering for calculating the critical speed of vehicles on curved paths. The critical speed is determined by balancing the centripetal force and the frictional force between the tires and the road:
\[ v_c = \sqrt{\mu g R} \]
where \( v_c \) is the critical speed, \( \mu \) is the coefficient of friction, \( g \) is the acceleration due to gravity, and \( R \) is the radius of the curve.
5. Aerospace Engineering
In aerospace engineering, the square root function is used in the calculation of the Mach number, which is the ratio of an object's speed to the speed of sound in the surrounding medium. The Mach number is critical for designing and analyzing aircraft performance:
\[ M = \frac{v}{\sqrt{\gamma R T}} \]
where \( M \) is the Mach number, \( v \) is the object's speed, \( \gamma \) is the specific heat ratio, \( R \) is the specific gas constant, and \( T \) is the temperature.
6. Environmental Engineering
In environmental engineering, square roots are used to model the dispersion of pollutants in the atmosphere. The dispersion model often involves Gaussian plume models, where the standard deviation of the distribution is a function of the square root of the time elapsed:
\[ \sigma_y = \sqrt{2Dt} \]
where \( \sigma_y \) is the standard deviation in the lateral direction, \( D \) is the diffusion coefficient, and \( t \) is the time.
These examples illustrate the diverse applications of square roots in engineering, highlighting their importance in calculations that ensure safety, efficiency, and performance in engineering projects.
Square Roots in Daily Life
The square root of 202, approximately 14.21, has various practical applications in daily life. Understanding square roots can enhance problem-solving skills and provide insights into various real-world scenarios.
1. Home Improvement and DIY Projects
Square roots are often used in home improvement and DIY projects. For instance:
- Area Calculations: When you need to determine the dimensions of a square area, such as for tiling a floor or painting a wall, the square root helps find the side length from the area. If a room is 202 square feet, the side length of a square room would be approximately 14.21 feet.
- Diagonal Measurements: Knowing the square root is useful for calculating diagonal distances. For a square with sides of 14.21 feet, the diagonal can be found using the Pythagorean theorem: √(14.212 + 14.212).
2. Finance and Investment
In finance, square roots are used to compute various financial metrics and risk assessments:
- Standard Deviation: This statistical measure, used to gauge market volatility, involves square roots. The square root of the variance provides the standard deviation, giving investors insights into investment risks.
- Compound Interest: The formula for compound interest includes roots when calculating the growth rate over time.
3. Sports and Fitness
Square roots are applied in sports and fitness for accurate measurements and performance analysis:
- Training Regimens: Athletes use square roots to analyze and optimize training intensities, ensuring balanced workout routines.
- Field Dimensions: Understanding the dimensions of sports fields, such as calculating the diagonal of a rectangular field, involves square roots.
4. Cooking and Baking
Precision in cooking and baking can be enhanced with the use of square roots:
- Recipe Adjustments: When scaling recipes up or down, especially for baking, accurate measurements are crucial. For example, doubling a recipe may require understanding the square root of ingredient quantities to maintain proportions.
5. Technology and Engineering
Square roots are fundamental in technology and engineering, particularly in design and diagnostics:
- Signal Processing: Engineers use square roots to analyze signal strength and noise levels, ensuring clear communication and data transmission.
- Material Strength: Calculations involving the stress and strain on materials often use square roots to predict performance and safety thresholds.
6. Nature and Environmental Studies
Square roots appear in nature and environmental studies, helping to understand natural patterns and phenomena:
- Population Studies: Ecologists use square roots to model population growth and distribution, aiding in conservation efforts.
- Geometric Growth: The growth patterns of certain plants and natural formations, like crystals, follow principles involving square roots.
In summary, the square root of 202, like many other mathematical concepts, has diverse applications in everyday life. From practical household tasks to complex financial and engineering problems, understanding and using square roots can provide valuable insights and solutions.
Conclusion
The journey to understanding the square root of 202 reveals not only a specific numerical value but also the broader significance of square roots in various fields. The square root of 202, approximately 14.2127, demonstrates the concept of finding a number which, when multiplied by itself, returns the original number. This process is fundamental in algebra and essential for various practical applications.
Through this guide, we've explored different methods to calculate the square root of 202, from manual techniques like the long division method to the convenience of calculators and computer functions. We've also delved into the importance of square roots in daily life and their extensive use in engineering, scientific research, and beyond.
Understanding square roots equips us with tools to solve real-world problems, from architectural design to financial modeling, and enhances our mathematical literacy. As we conclude, it’s evident that the seemingly simple concept of a square root holds a powerful place in both theoretical and applied mathematics, proving that foundational knowledge can have widespread and impactful applications.

SQUARE ROOT OF 202
SQUARE ROOT OF 202
How To Calculate Square Roots - Numerals That Changed Math Forever
Find the square root of 200×201×202×203+1
"`sqrt(53824)=?`(a) 202 (b) 232 (c) 242 (d) 332"
Indian vs Japanese Maths 🔥| Vedic Maths Trick for Fast Calculation | Speed Maths #trending #shorts
READ MORE: