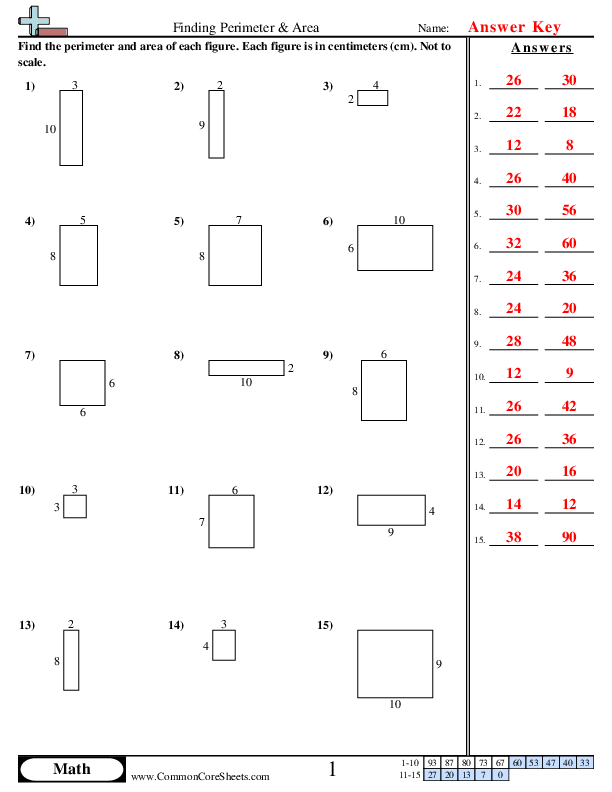
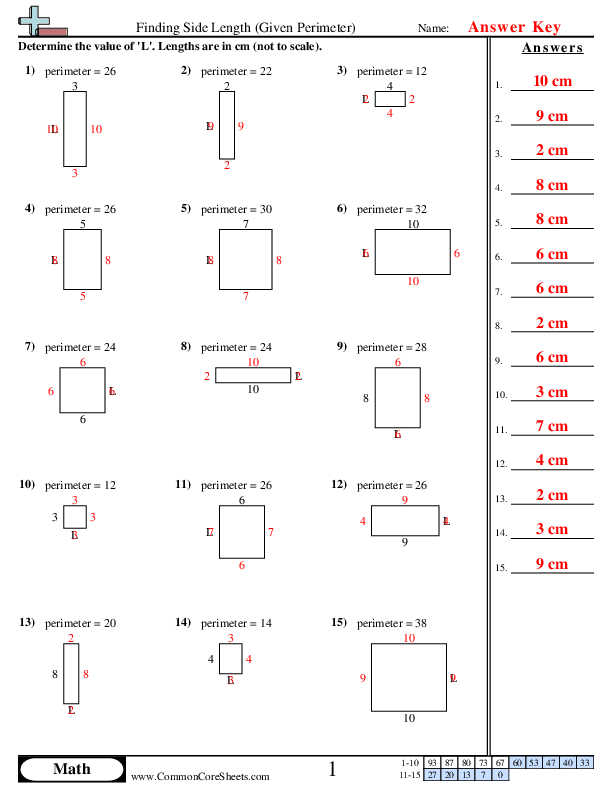
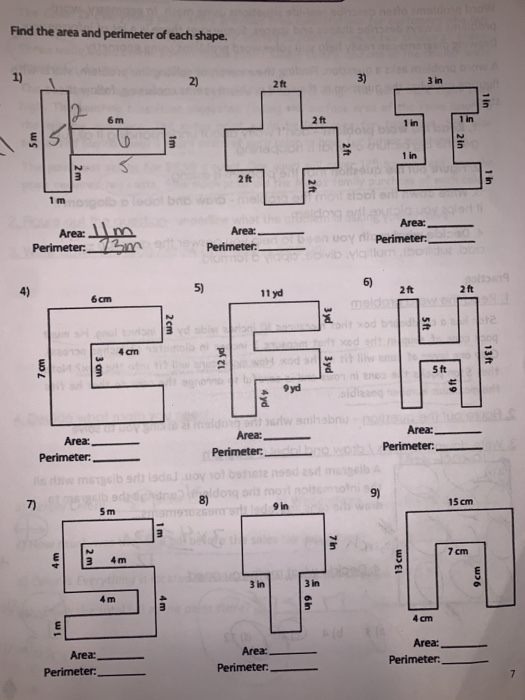
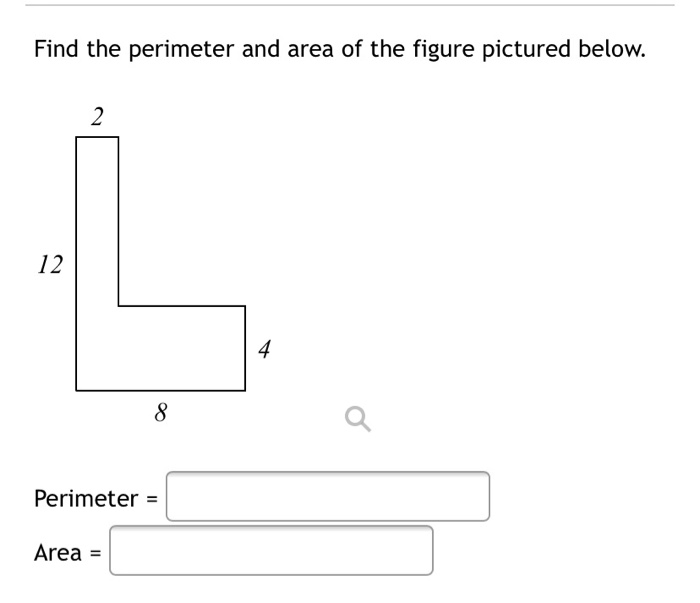
Topic area and perimeter on the coordinate plane: Discover the essentials of calculating area and perimeter on the coordinate plane with our detailed guide. Perfect for students and educators alike, this article breaks down key concepts, offers practical examples, and provides interactive tools to enhance your understanding. Dive in to master these fundamental geometry skills and boost your confidence in coordinate geometry.
Table of Content
- Area and Perimeter on the Coordinate Plane
- Introduction to Coordinate Plane
- Understanding Coordinates
- Plotting Points on the Coordinate Plane
- Basics of Area Calculation
- Calculating Area of Polygons
- Area of Rectangles and Squares
- Area of Triangles
- Area of Irregular Shapes
- Basics of Perimeter Calculation
- Calculating Perimeter of Polygons
- Perimeter of Rectangles and Squares
- Perimeter of Triangles
- Perimeter of Irregular Shapes
- Using Distance Formula for Perimeter
- Applications of Area and Perimeter
- Word Problems and Practical Examples
- Interactive Tools and Resources
- Common Mistakes and How to Avoid Them
- YOUTUBE: Video này giải thích cách tính diện tích và chu vi trên mặt phẳng tọa độ, giúp bạn hiểu rõ hơn về hình học và toán học.
Area and Perimeter on the Coordinate Plane
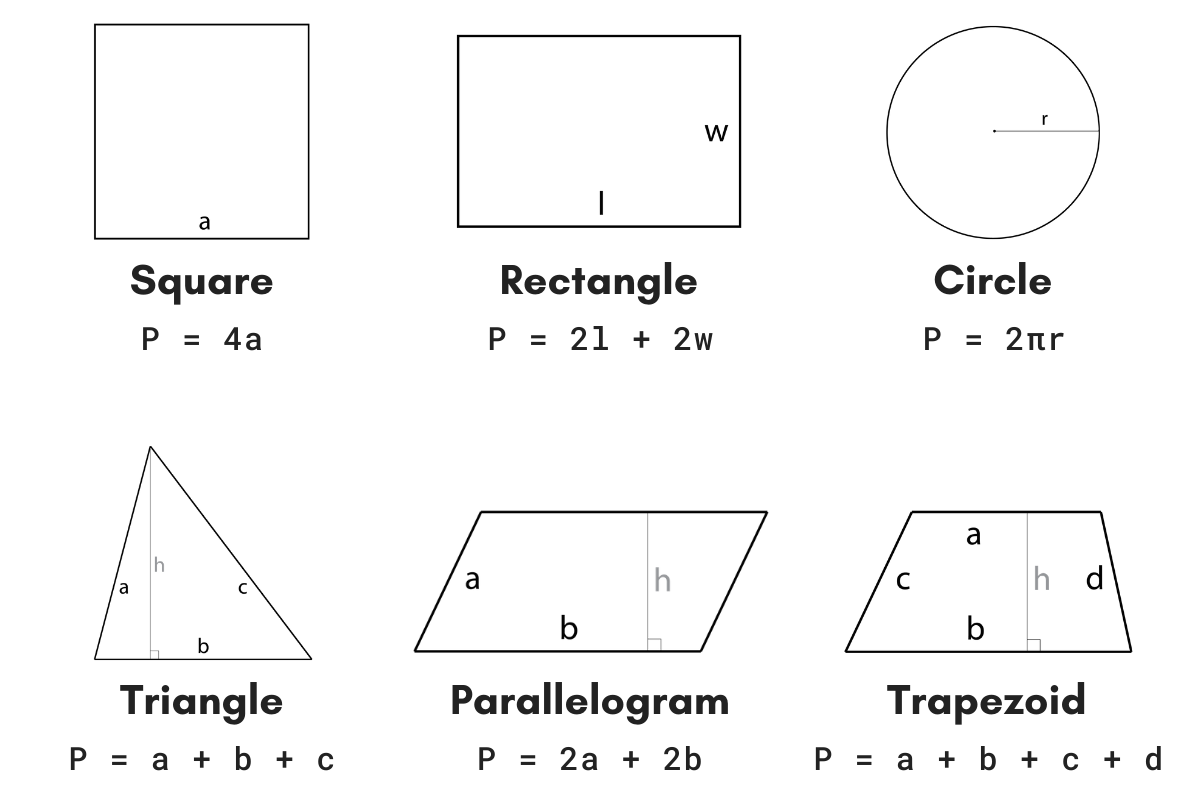
Calculating the area and perimeter of shapes on the coordinate plane involves using the coordinates of the vertices to determine side lengths and then applying standard geometric formulas. Here is a comprehensive guide on how to approach these calculations.
Understanding the Basics
When working with shapes on the coordinate plane, you often need to:
- Determine the coordinates of the vertices.
- Use the distance formula to calculate the lengths of sides.
- Apply geometric formulas to find the area and perimeter.
Distance Formula
The distance formula is essential for finding the length of sides. Given two points \((x_1, y_1)\) and \((x_2, y_2)\), the distance \(d\) between them is:
$$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$
Example: Rectangle
Consider a rectangle with vertices at \((1, 2)\), \((1, 6)\), \((5, 6)\), and \((5, 2)\).
To find the lengths of the sides:
- Length: $$l = \sqrt{(5 - 1)^2 + (6 - 6)^2} = 4$$ units
- Width: $$w = \sqrt{(1 - 1)^2 + (6 - 2)^2} = 4$$ units
Using these, the perimeter \(P\) and area \(A\) are:
- Perimeter: $$P = 2(l + w) = 2(4 + 4) = 16$$ units
- Area: $$A = l \times w = 4 \times 4 = 16$$ square units
Example: Triangle
For a triangle with vertices at \((2, 3)\), \((6, 7)\), and \((8, 3)\):
Use the distance formula to find the lengths of the sides:
- Side 1: $$\sqrt{(6 - 2)^2 + (7 - 3)^2} = \sqrt{16 + 16} = \sqrt{32} = 5.66$$ units
- Side 2: $$\sqrt{(8 - 6)^2 + (3 - 7)^2} = \sqrt{4 + 16} = \sqrt{20} = 4.47$$ units
- Side 3: $$\sqrt{(8 - 2)^2 + (3 - 3)^2} = 6$$ units
Using these, the perimeter \(P\) is:
- Perimeter: $$P = 5.66 + 4.47 + 6 = 16.13$$ units
To find the area \(A\), use the formula for the area of a triangle with vertices \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\):
$$A = \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$$
Substituting in the values:
$$A = \frac{1}{2} |2(7 - 3) + 6(3 - 3) + 8(3 - 7)| = \frac{1}{2} |8 + 0 - 32| = \frac{1}{2} \times 24 = 12$$ square units
Composite Figures
For composite figures, break them down into simpler shapes like rectangles and triangles, calculate the area and perimeter for each, and then sum them up.
Example: For a shape that can be divided into a rectangle and a triangle, calculate the area and perimeter of each part separately, then add them to get the total area and perimeter.
Summary
Using the coordinate plane to find area and perimeter involves a combination of the distance formula and standard geometric formulas. Practice these steps to gain proficiency:
- Identify vertices' coordinates.
- Calculate side lengths using the distance formula.
- Apply appropriate formulas to find area and perimeter.
With these skills, solving problems on the coordinate plane becomes a systematic and manageable process.

READ MORE:
Introduction to Coordinate Plane
The coordinate plane, also known as the Cartesian plane, is a two-dimensional surface defined by two perpendicular axes: the x-axis (horizontal) and the y-axis (vertical). These axes intersect at a point called the origin, denoted by (0,0).
To understand the coordinate plane, follow these steps:
- Identify the Axes: The x-axis runs horizontally, and the y-axis runs vertically. The point where they intersect is the origin.
- Plotting Points: Points on the coordinate plane are represented by ordered pairs (x, y). The first number, x, denotes the horizontal distance from the origin, and the second number, y, denotes the vertical distance.
- Quadrants: The coordinate plane is divided into four quadrants:
- Quadrant I: Both x and y are positive.
- Quadrant II: x is negative, y is positive.
- Quadrant III: Both x and y are negative.
- Quadrant IV: x is positive, y is negative.
- Example: To plot the point (3, 4), start at the origin. Move 3 units to the right (positive x-direction) and 4 units up (positive y-direction). Place a dot at this location.
Understanding the coordinate plane is essential for solving problems involving area and perimeter of shapes plotted on this plane. It provides a visual way to see the relationships between geometric figures and their measurements.
Understanding Coordinates
Coordinates are a set of values that show an exact position on a coordinate plane. The coordinate system is used to uniquely determine the position of a point or other geometric element in a plane using an ordered pair of numbers.
To understand coordinates, follow these steps:
- Coordinate Pair: Each point on the coordinate plane is represented by an ordered pair \((x, y)\), where \(x\) is the horizontal distance from the origin and \(y\) is the vertical distance.
- Positive and Negative Values:
- Positive \(x\) values are to the right of the origin.
- Negative \(x\) values are to the left of the origin.
- Positive \(y\) values are above the origin.
- Negative \(y\) values are below the origin.
- Plotting Coordinates: To plot a point given its coordinates \((x, y)\):
- Start at the origin \((0,0)\).
- Move horizontally to the \(x\) value: right if \(x\) is positive, left if \(x\) is negative.
- Move vertically to the \(y\) value: up if \(y\) is positive, down if \(y\) is negative.
- Mark the point at the final position.
- Example: To plot the point \((3, -2)\), start at the origin. Move 3 units to the right (positive \(x\)) and 2 units down (negative \(y\)). Place a dot at this location.
Understanding how to read and plot coordinates is fundamental for working with the coordinate plane, as it allows you to precisely locate points and define shapes necessary for calculating areas and perimeters.
Plotting Points on the Coordinate Plane
Plotting points on the coordinate plane is an essential skill for understanding geometry and algebra. Follow these detailed steps to accurately plot points:
- Understand the Coordinate System:
- The horizontal axis is the x-axis.
- The vertical axis is the y-axis.
- The point where these axes intersect is the origin \((0,0)\).
- Identify the Coordinates: Each point is represented by an ordered pair \((x, y)\), where \(x\) indicates the horizontal position and \(y\) indicates the vertical position.
- Move Horizontally to the x-value:
- If \(x\) is positive, move right from the origin.
- If \(x\) is negative, move left from the origin.
- Move Vertically to the y-value:
- If \(y\) is positive, move up from the x-axis.
- If \(y\) is negative, move down from the x-axis.
- Plot the Point: Mark the point where the horizontal and vertical movements intersect.
- Example: To plot the point \((4, -3)\):
- Start at the origin \((0,0)\).
- Move 4 units to the right (positive \(x\)).
- Move 3 units down (negative \(y\)).
- Place a dot at this final position.
By following these steps, you can accurately plot any point on the coordinate plane. This skill is crucial for graphing equations, visualizing geometric shapes, and solving real-world problems involving area and perimeter.
Basics of Area Calculation
Calculating the area of shapes on the coordinate plane involves determining the space enclosed within the shape's boundaries. Here are the basic steps and principles for calculating area:
- Identify the Shape: Determine the type of shape you are dealing with (e.g., rectangle, triangle, polygon).
- Use Appropriate Formulas: Each shape has a specific formula for area calculation. Here are some common ones:
- Rectangle: The area \(A\) is calculated using the formula \(A = \text{length} \times \text{width}\).
- Triangle: The area \(A\) is calculated using the formula \(A = \frac{1}{2} \times \text{base} \times \text{height}\).
- Parallelogram: The area \(A\) is calculated using the formula \(A = \text{base} \times \text{height}\).
- Polygon: For complex polygons, divide the shape into simpler components (like triangles) and sum their areas.
- Plot and Label Points: On the coordinate plane, accurately plot and label all vertices of the shape.
- Apply the Distance Formula: If needed, use the distance formula to find lengths of sides. The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Calculate the Area: Using the identified shape and appropriate formula, calculate the area. For example:
- Example for a Rectangle: If the vertices of a rectangle are \((1,1)\), \((1,4)\), \((5,1)\), and \((5,4)\), calculate the length and width using the distance formula, then find the area.
Understanding these basics will help you accurately calculate the area of various shapes on the coordinate plane, which is a fundamental skill in geometry and its applications.
Calculating Area of Polygons
Calculating the area of polygons on the coordinate plane can be done using various methods. Here, we will explore the step-by-step process using the Shoelace formula, also known as Gauss's area formula for polygons.
Consider a polygon with vertices \( (x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n) \) listed in counterclockwise order. The Shoelace formula is given by:
\[
\text{Area} = \frac{1}{2} \left| \sum_{i=1}^{n-1} (x_i y_{i+1} - y_i x_{i+1}) + (x_n y_1 - y_n x_1) \right|
\]
Follow these steps to calculate the area:
- List the coordinates of the vertices in order.
- Apply the Shoelace formula by substituting the coordinates into the formula.
- Calculate the sum inside the absolute value and then multiply by \( \frac{1}{2} \).
- Take the absolute value of the result to ensure the area is non-negative.
For example, let's find the area of a polygon with vertices \( (2, 1), (4, 5), (7, 8), (6, 3) \):
| Vertex | \( x \) | \( y \) |
|---|---|---|
| 1 | 2 | 1 |
| 2 | 4 | 5 |
| 3 | 7 | 8 |
| 4 | 6 | 3 |
Now, apply the Shoelace formula:
\[
\begin{align*}
\text{Area} & = \frac{1}{2} \left| (2 \cdot 5 + 4 \cdot 8 + 7 \cdot 3 + 6 \cdot 1) - (1 \cdot 4 + 5 \cdot 7 + 8 \cdot 6 + 3 \cdot 2) \right| \\
& = \frac{1}{2} \left| (10 + 32 + 21 + 6) - (4 + 35 + 48 + 6) \right| \\
& = \frac{1}{2} \left| 69 - 93 \right| \\
& = \frac{1}{2} \left| -24 \right| \\
& = \frac{1}{2} \cdot 24 \\
& = 12
\end{align*}
\]
Therefore, the area of the polygon is 12 square units.
Using this method, you can calculate the area for any polygon by following these steps and applying the Shoelace formula.
Area of Rectangles and Squares
Understanding the area of rectangles and squares on the coordinate plane is essential for various mathematical applications. Here, we will discuss how to calculate the area of these shapes using their coordinates.
Rectangles
To find the area of a rectangle, you need to determine its width and height. These can be calculated using the coordinates of the vertices of the rectangle. Follow these steps:
- Identify the coordinates of the vertices of the rectangle, say \( (x_1, y_1) \), \( (x_2, y_2) \), \( (x_3, y_3) \), and \( (x_4, y_4) \).
- Calculate the width of the rectangle using the distance formula for horizontal distance: \( \text{width} = |x_2 - x_1| \) or \( |x_4 - x_3| \).
- Calculate the height of the rectangle using the distance formula for vertical distance: \( \text{height} = |y_3 - y_1| \) or \( |y_4 - y_2| \).
- Use the area formula for rectangles: \( \text{Area} = \text{width} \times \text{height} \).
For example, if the vertices of the rectangle are at \( (1, 2) \), \( (1, 5) \), \( (4, 5) \), and \( (4, 2) \), then:
- \(\text{Width} = |4 - 1| = 3\)
- \(\text{Height} = |5 - 2| = 3\)
- \(\text{Area} = 3 \times 3 = 9\)
Squares
For squares, all sides are equal, so you only need to find the length of one side and square it to find the area. Follow these steps:
- Identify the coordinates of two adjacent vertices of the square, say \( (x_1, y_1) \) and \( (x_2, y_2) \).
- Calculate the side length using the distance formula: \[ \text{side length} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Use the area formula for squares: \( \text{Area} = \text{side length}^2 \).
For example, if the vertices of the square are at \( (1, 2) \) and \( (4, 2) \), then:
- \(\text{Side length} = |4 - 1| = 3\)
- \(\text{Area} = 3^2 = 9\)
These methods ensure accurate calculations of the area for rectangles and squares on the coordinate plane using their vertex coordinates.
Area of Triangles
To find the area of a triangle on the coordinate plane, we use the formula that involves the coordinates of its vertices. Given a triangle with vertices at coordinates \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\), the formula for the area is:
\[
A = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right|
\]
This formula calculates the absolute value to ensure the area is always positive. Here are the steps to calculate the area of a triangle using this method:
- Identify the coordinates of the three vertices of the triangle.
- Substitute the coordinates into the formula.
- Perform the calculations inside the absolute value sign.
- Take the absolute value of the result.
- Multiply by \(\frac{1}{2}\) to get the area.
Let's consider an example to illustrate this method:
Example: Find the area of a triangle with vertices at \(A(1, 2)\), \(B(4, 6)\), and \(C(5, 3)\).
Substitute the coordinates into the formula:
\[
A = \frac{1}{2} \left| 1(6 - 3) + 4(3 - 2) + 5(2 - 6) \right|
\]
Calculate each term:
- \(1(6 - 3) = 1 \cdot 3 = 3\)
- \(4(3 - 2) = 4 \cdot 1 = 4\)
- \(5(2 - 6) = 5 \cdot (-4) = -20\)
Sum the terms and take the absolute value:
\[
A = \frac{1}{2} \left| 3 + 4 - 20 \right| = \frac{1}{2} \left| -13 \right| = \frac{1}{2} \cdot 13 = 6.5
\]
Thus, the area of the triangle is 6.5 square units.
Another method to find the area of a triangle when you know the lengths of the sides is using Heron's formula. This involves three steps:
- Calculate the length of each side using the distance formula:
- Compute the semi-perimeter \(s\) of the triangle:
- Apply Heron's formula to find the area:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
\[
s = \frac{a + b + c}{2}
\]
\[
A = \sqrt{s(s - a)(s - b)(s - c)}
\]
For triangles on a grid, you can also use the "box method," which involves drawing the smallest rectangle that encloses the triangle, calculating the area of the rectangle, and subtracting the areas of the right triangles and rectangles outside the main triangle.
Area of Irregular Shapes
Calculating the area of irregular shapes on the coordinate plane involves breaking down the shape into simpler geometric figures or applying specific formulas. Here, we will discuss two primary methods: using unit squares and the shoelace formula.
Using Unit Squares
This method is useful for shapes with curved edges or those that do not fit easily into standard polygons. Here’s how you can calculate the area:
- Overlay a grid of unit squares on the shape.
- Count the full unit squares inside the shape.
- Estimate the area covered by partial squares. Count them if they are more than half-covered.
- Add the areas together to get the total area of the shape.
For example, if a shape contains 6 fully covered unit squares and 4 partially covered squares that are more than half-filled, the total area will be approximately 10 unit squares.
Dividing into Regular Shapes
Many irregular shapes can be divided into a combination of triangles, rectangles, and other polygons. Follow these steps:
- Identify and draw lines to divide the irregular shape into known shapes.
- Calculate the area of each known shape using standard formulas:
- Rectangle: \( \text{Area} = \text{length} \times \text{width} \)
- Triangle: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
- Circle/Semicircle: \( \text{Area} = \pi r^2 \) or \( \frac{1}{2} \pi r^2 \)
- Sum the areas of all the smaller shapes to find the total area of the irregular shape.
Shoelace Formula
The shoelace formula is a more advanced method suitable for calculating the area of any polygon when the coordinates of its vertices are known. Here’s the formula:
\[ \text{Area} = \frac{1}{2} \left| \sum_{i=1}^{n-1} (x_i y_{i+1} - y_i x_{i+1}) + (x_n y_1 - y_n x_1) \right| \]
Steps to apply the formula:
- List the coordinates of the vertices in order, repeating the first vertex at the end.
- Multiply the x-coordinate of each vertex by the y-coordinate of the next vertex and sum these products.
- Multiply the y-coordinate of each vertex by the x-coordinate of the next vertex and sum these products.
- Subtract the second sum from the first sum.
- Take the absolute value of the result and divide by 2 to get the area.
For example, consider a polygon with vertices at \((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\). Applying the shoelace formula will yield the area of this polygon.
By using these methods, you can effectively calculate the area of various irregular shapes on the coordinate plane.

Basics of Perimeter Calculation
The perimeter of a shape on the coordinate plane is the total distance around the shape. To find the perimeter, you need to determine the length of each side and then sum these lengths. Here are the steps to calculate the perimeter of various shapes on the coordinate plane:
Steps to Calculate Perimeter
-
Identify the vertices of the shape: List the coordinates of each vertex of the shape. For example, for a rectangle with vertices at \( A(x_1, y_1) \), \( B(x_2, y_2) \), \( C(x_3, y_3) \), and \( D(x_4, y_4) \).
-
Use the distance formula to find the lengths of the sides: The distance formula between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by:
\[
\text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]Apply this formula to each pair of adjacent vertices to find the lengths of the sides.
-
Sum the lengths of all sides: Once you have the lengths of all sides, add them together to get the perimeter.
For example, if the lengths of the sides of a rectangle are \( l \) and \( w \), the perimeter \( P \) is:
\[
P = 2l + 2w
\]
Example
Consider a rectangle on the coordinate plane with vertices at \((2, 3)\), \((2, 7)\), \((5, 7)\), and \((5, 3)\).
- Calculate the length of one side using the distance formula:
- Calculate the length of the adjacent side:
- Sum the lengths of all sides to find the perimeter:
\[
\text{Length} = \sqrt{(5 - 2)^2 + (7 - 7)^2} = \sqrt{3^2 + 0^2} = \sqrt{9} = 3
\]
\[
\text{Width} = \sqrt{(2 - 2)^2 + (7 - 3)^2} = \sqrt{0 + 4^2} = \sqrt{16} = 4
\]
\[
P = 2 \times 3 + 2 \times 4 = 6 + 8 = 14 \text{ units}
\]
Special Cases
- Squares and Rectangles: For squares, all sides are equal, so the perimeter is four times the side length. For rectangles, use the formula \( P = 2l + 2w \).
- Triangles: Sum the lengths of all three sides. For right triangles, you can also use the Pythagorean theorem to find the length of the hypotenuse.
- Irregular Shapes: Break down the shape into simpler components if necessary, calculate the perimeter of each component, and then sum them up.
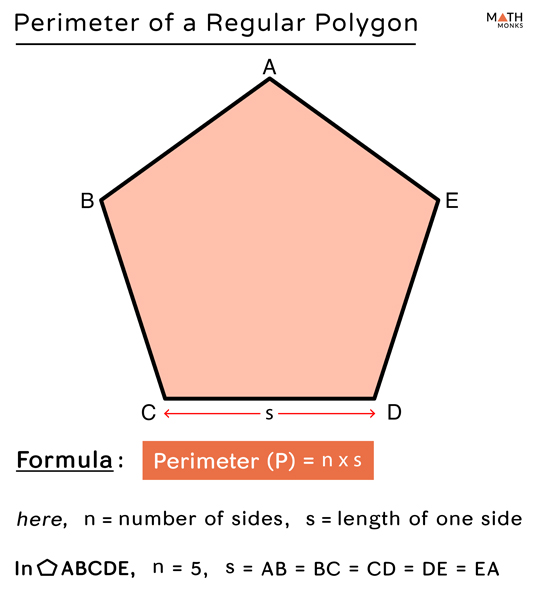
Calculating Perimeter of Polygons
Calculating the perimeter of polygons involves summing the lengths of all their sides. Polygons can be regular, with all sides and angles equal, or irregular, with sides and angles of different lengths and measures. Below are the steps to calculate the perimeter of both regular and irregular polygons on the coordinate plane.
Steps for Calculating the Perimeter of a Regular Polygon
- Determine the number of sides \( n \) of the polygon.
- Measure the length of one side \( s \).
- Use the formula:
\[ \text{Perimeter} = n \times s \]
For example, for a square with side length \( s = 5 \) units:
\[
\text{Perimeter} = 4 \times 5 = 20 \text{ units}
\]
Steps for Calculating the Perimeter of an Irregular Polygon
- List all the vertices of the polygon and label them as \((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\).
- Calculate the distance between each pair of consecutive vertices using the distance formula: \[ \text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Sum all the distances to get the perimeter: \[ \text{Perimeter} = \sum_{i=1}^{n-1} \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} + \sqrt{(x_1 - x_n)^2 + (y_1 - y_n)^2} \]
For instance, for a polygon with vertices at \((1, 2)\), \((4, 6)\), and \((7, 2)\):
- Calculate distances between each pair of vertices: \[ \sqrt{(4-1)^2 + (6-2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5 \text{ units} \] \[ \sqrt{(7-4)^2 + (2-6)^2} = \sqrt{3^2 + (-4)^2} = \sqrt{9 + 16} = 5 \text{ units} \] \[ \sqrt{(1-7)^2 + (2-2)^2} = \sqrt{(-6)^2 + 0^2} = 6 \text{ units} \]
- Sum the distances: \[ \text{Perimeter} = 5 + 5 + 6 = 16 \text{ units} \]
Special Cases: Using the Distance Formula
When dealing with vertices on a coordinate plane, the distance formula is essential. This formula helps to compute the lengths of sides accurately, especially when they are not aligned with the axes.
The distance formula is given by:
\[
D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
This approach ensures precise calculation of the lengths of sides, crucial for determining the perimeter of complex polygons.
Perimeter of Rectangles and Squares
Calculating the perimeter of rectangles and squares on the coordinate plane involves determining the lengths of the sides using their coordinates and then summing these lengths.
Steps to Calculate the Perimeter of Rectangles
- Identify the coordinates of the vertices of the rectangle. For example, let's say the vertices are \( A(x_1, y_1) \), \( B(x_2, y_2) \), \( C(x_3, y_3) \), and \( D(x_4, y_4) \).
- Calculate the lengths of the sides using the distance formula:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\] - Find the lengths of all four sides. Since opposite sides of a rectangle are equal, calculate the length and width using:
- Length \( l = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
- Width \( w = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \)
- Sum the lengths of all sides to get the perimeter:
\[
P = 2 \cdot (l + w)
\]
Example Calculation
Suppose we have a rectangle with vertices at \( A(1, 2) \), \( B(1, 5) \), \( C(4, 5) \), and \( D(4, 2) \).
- Length: \( l = \sqrt{(1 - 1)^2 + (5 - 2)^2} = \sqrt{0 + 9} = 3 \)
- Width: \( w = \sqrt{(4 - 1)^2 + (5 - 5)^2} = \sqrt{9 + 0} = 3 \)
- Perimeter: \( P = 2 \cdot (3 + 3) = 2 \cdot 6 = 12 \)
Steps to Calculate the Perimeter of Squares
- Identify the coordinates of the vertices of the square. For example, let's say the vertices are \( A(x_1, y_1) \), \( B(x_2, y_2) \), \( C(x_3, y_3) \), and \( D(x_4, y_4) \).
- Calculate the length of one side using the distance formula:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\] - Since all sides of a square are equal, calculate the perimeter as:
where \( s \) is the length of one side.
\[
P = 4 \cdot s
\]
Example Calculation
Suppose we have a square with vertices at \( A(2, 2) \), \( B(2, 5) \), \( C(5, 5) \), and \( D(5, 2) \).
- Side length: \( s = \sqrt{(2 - 2)^2 + (5 - 2)^2} = \sqrt{0 + 9} = 3 \)
- Perimeter: \( P = 4 \cdot 3 = 12 \)
Perimeter of Triangles
Calculating the perimeter of a triangle on the coordinate plane involves finding the sum of the lengths of its sides. Here's a detailed step-by-step guide:
-
Identify the vertices:
Determine the coordinates of the three vertices of the triangle. Let's denote them as \( A(x_1, y_1) \), \( B(x_2, y_2) \), and \( C(x_3, y_3) \).
-
Calculate the lengths of the sides:
Use the distance formula to calculate the length of each side of the triangle. The distance formula between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]- Length of side \( AB \): \[ AB = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Length of side \( BC \): \[ BC = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \]
- Length of side \( CA \): \[ CA = \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} \]
-
Sum the lengths:
Add the lengths of all three sides to get the perimeter of the triangle:
\[
\text{Perimeter} = AB + BC + CA
\]
For example, if we have a triangle with vertices at \( A(1, 2) \), \( B(4, 6) \), and \( C(7, 2) \), the perimeter calculation would be as follows:
-
Calculate \( AB \):
\[
AB = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\] -
Calculate \( BC \):
\[
BC = \sqrt{(7 - 4)^2 + (2 - 6)^2} = \sqrt{3^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\] -
Calculate \( CA \):
\[
CA = \sqrt{(7 - 1)^2 + (2 - 2)^2} = \sqrt{6^2 + 0^2} = \sqrt{36} = 6
\] -
Sum the lengths:
\[
\text{Perimeter} = 5 + 5 + 6 = 16
\]
Thus, the perimeter of the triangle is 16 units.
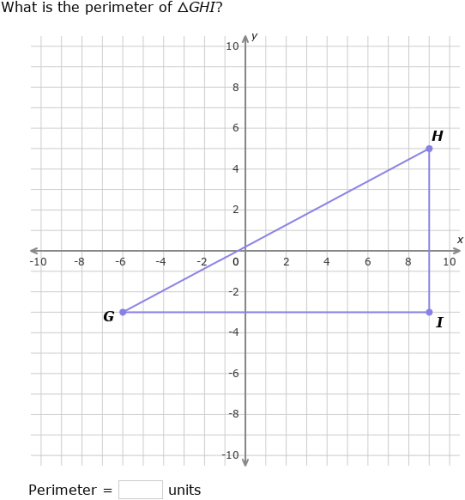
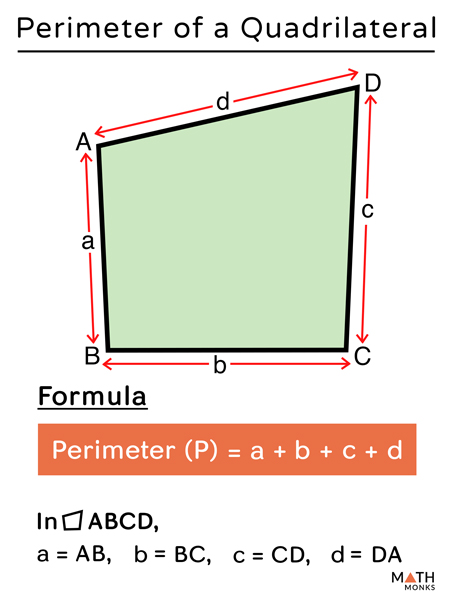
Perimeter of Irregular Shapes
Calculating the perimeter of irregular shapes on the coordinate plane involves summing the lengths of all sides of the shape. Here’s a step-by-step guide to finding the perimeter of such shapes:
-
Identify the vertices:
List the coordinates of all vertices of the irregular shape. For example, consider a quadrilateral with vertices at
(x_1, y_1),(x_2, y_2),(x_3, y_3), and(x_4, y_4). -
Calculate the distance between each pair of consecutive vertices:
Use the distance formula to find the length of each side. The distance formula between two points
(x_1, y_1)and(x_2, y_2)is:\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]- Distance between
(x_1, y_1)and(x_2, y_2): - Distance between
(x_2, y_2)and(x_3, y_3): - Distance between
(x_3, y_3)and(x_4, y_4): - Distance between
(x_4, y_4)and(x_1, y_1):
\[
d_{12} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]\[
d_{23} = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2}
\]\[
d_{34} = \sqrt{(x_4 - x_3)^2 + (y_4 - y_3)^2}
\]\[
d_{41} = \sqrt{(x_4 - x_1)^2 + (y_4 - y_1)^2}
\] - Distance between
-
Sum the lengths of all sides:
Add the distances calculated in the previous step to find the total perimeter of the irregular shape:
\[
\text{Perimeter} = d_{12} + d_{23} + d_{34} + d_{41}
\]
Here’s an example to illustrate the process:
-
Example:
Consider an irregular shape with vertices at
(1, 2),(4, 5),(6, 2), and(3, 0).-
Calculate the distances:
- Distance between
(1, 2)and(4, 5): - Distance between
(4, 5)and(6, 2): - Distance between
(6, 2)and(3, 0): - Distance between
(3, 0)and(1, 2):
\[
d_{12} = \sqrt{(4 - 1)^2 + (5 - 2)^2} = \sqrt{3^2 + 3^2} = \sqrt{18} = 3\sqrt{2}
\]\[
d_{23} = \sqrt{(6 - 4)^2 + (2 - 5)^2} = \sqrt{2^2 + (-3)^2} = \sqrt{13}
\]\[
d_{34} = \sqrt{(3 - 6)^2 + (0 - 2)^2} = \sqrt{(-3)^2 + (-2)^2} = \sqrt{13}
\]\[
d_{41} = \sqrt{(1 - 3)^2 + (2 - 0)^2} = \sqrt{(-2)^2 + 2^2} = \sqrt{8} = 2\sqrt{2}
\] - Distance between
-
Sum the distances:
Add the lengths of all sides to find the perimeter:
\[
\text{Perimeter} = 3\sqrt{2} + \sqrt{13} + \sqrt{13} + 2\sqrt{2} = 5\sqrt{2} + 2\sqrt{13}
\]
-
Calculate the distances:
Thus, the perimeter of the irregular shape is \( 5\sqrt{2} + 2\sqrt{13} \).
Using Distance Formula for Perimeter
The distance formula is essential for calculating the perimeter of shapes on the coordinate plane. This formula helps determine the distance between any two points, which can be summed to find the total perimeter. Here’s how you can use the distance formula step-by-step:
-
Understand the distance formula:
The distance \(d\) between two points \((x_1, y_1)\) and \((x_2, y_2)\) on the coordinate plane is given by:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\] -
Identify the vertices of the shape:
List the coordinates of all vertices. For example, a pentagon with vertices at \((x_1, y_1)\), \((x_2, y_2)\), \((x_3, y_3)\), \((x_4, y_4)\), and \((x_5, y_5)\).
-
Calculate the distance between consecutive vertices:
Apply the distance formula to each pair of consecutive vertices to find the lengths of the sides:
- Distance between \((x_1, y_1)\) and \((x_2, y_2)\):
- Distance between \((x_2, y_2)\) and \((x_3, y_3)\):
- Distance between \((x_3, y_3)\) and \((x_4, y_4)\):
- Distance between \((x_4, y_4)\) and \((x_5, y_5)\):
- Distance between \((x_5, y_5)\) and \((x_1, y_1)\):
\[
d_{12} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]\[
d_{23} = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2}
\]\[
d_{34} = \sqrt{(x_4 - x_3)^2 + (y_4 - y_3)^2}
\]\[
d_{45} = \sqrt{(x_5 - x_4)^2 + (y_5 - y_4)^2}
\]\[
d_{51} = \sqrt{(x_5 - x_1)^2 + (y_5 - y_1)^2}
\] -
Sum the distances:
Add the distances of all sides to find the total perimeter:
\[
\text{Perimeter} = d_{12} + d_{23} + d_{34} + d_{45} + d_{51}
\]
Here’s a detailed example to clarify:
-
Example:
Calculate the perimeter of a triangle with vertices at \((1, 2)\), \((4, 6)\), and \((7, 3)\).
-
Distance between \((1, 2)\) and \((4, 6)\):
\[
d_{12} = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\] -
Distance between \((4, 6)\) and \((7, 3)\):
\[
d_{23} = \sqrt{(7 - 4)^2 + (3 - 6)^2} = \sqrt{3^2 + (-3)^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2}
\] -
Distance between \((7, 3)\) and \((1, 2)\):
\[
d_{31} = \sqrt{(7 - 1)^2 + (3 - 2)^2} = \sqrt{6^2 + 1^2} = \sqrt{36 + 1} = \sqrt{37}
\] -
Sum the distances:
Add the lengths of all sides to find the total perimeter:
\[
\text{Perimeter} = 5 + 3\sqrt{2} + \sqrt{37}
\]
-
Distance between \((1, 2)\) and \((4, 6)\):
The perimeter of the triangle is \( 5 + 3\sqrt{2} + \sqrt{37} \).
Applications of Area and Perimeter
The concepts of area and perimeter have numerous practical applications across various fields. Understanding these applications can help in solving real-world problems involving measurement and optimization. Here are some key applications:
-
Landscaping and Agriculture:
In landscaping, knowing the area of a plot of land helps in determining the amount of materials like soil, mulch, or sod required. For instance:
- Calculating Area for Planting: Determine the area to allocate space for different plants. For a rectangular garden bed with length \( l \) and width \( w \), the area \( A \) is:
- Fencing: Calculate the perimeter to determine the length of fencing needed around the plot. For a rectangular plot, the perimeter \( P \) is:
\[
A = l \times w
\]\[
P = 2l + 2w
\] -
Architecture and Construction:
In architecture, area and perimeter calculations are crucial for designing layouts and determining material quantities. Examples include:
- Floor Plans: Calculate the area of rooms to ensure proper use of space and placement of furniture. For example, the area of a triangular room with base \( b \) and height \( h \) is:
- Building Perimeters: Determine the perimeter to plan the exterior walls and roofing materials. For irregular shapes, sum the distances between consecutive vertices using the distance formula.
\[
A = \frac{1}{2} b \times h
\] -
Sports Fields and Courts:
Accurate measurements of sports fields and courts are essential for construction and maintenance. For example:
- Soccer Field: Calculate the area to ensure it meets regulations. A standard soccer field might be 100 meters long and 64 meters wide, so the area \( A \) is:
- Tennis Court: Calculate the perimeter to determine the amount of fencing needed around the court. For a standard tennis court, with length \( l \) and width \( w \), the perimeter \( P \) is:
\[
A = 100 \times 64 = 6400 \text{ square meters}
\]\[
P = 2l + 2w
\] -
Art and Design:
Artists and designers use area and perimeter calculations in creating patterns, designs, and layouts. For example:
- Creating Patterns: Calculate areas to design repeated patterns that fit within a specific space. For a repeating hexagonal pattern, where each hexagon has a side length \( s \), the area \( A \) of one hexagon is:
- Framing Art: Determine the perimeter of artwork to select appropriate frame sizes. For a rectangular piece of art, calculate the perimeter using the standard formula.
\[
A = \frac{3\sqrt{3}}{2} s^2
\] -
Environmental Studies:
In environmental science, area and perimeter calculations help in understanding habitats and ecosystems. Examples include:
- Estimating Habitat Size: Calculate the area of habitats to assess the space available for wildlife. For a circular habitat with radius \( r \), the area \( A \) is:
- Measuring Shoreline Length: Use the perimeter to understand the length of shorelines or boundaries in ecological studies.
\[
A = \pi r^2
\] -
Urban Planning:
Urban planners use area and perimeter calculations for efficient city layout and infrastructure development:
- City Blocks: Calculate the area and perimeter of city blocks for zoning and construction purposes.
- Parks and Recreational Areas: Determine the area of parks to plan facilities and green spaces. The perimeter helps in planning pathways and boundaries.
These applications show how the concepts of area and perimeter are integral to various fields, providing solutions and optimizations for real-world challenges.
Word Problems and Practical Examples
Understanding area and perimeter on the coordinate plane can be enhanced through practical examples and word problems. These exercises demonstrate the application of mathematical concepts in real-world scenarios. Here’s a detailed exploration of some word problems:
-
Finding the Area of a Triangle:
Problem: Given a triangle with vertices at \((1, 2)\), \((4, 5)\), and \((7, 2)\), calculate the area.
- Plot the points on the coordinate plane and visualize the triangle.
- Use the formula for the area of a triangle with vertices \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\):
- Substitute the coordinates into the formula:
- Therefore, the area of the triangle is \( 9 \) square units.
\[
\text{Area} = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right|
\]\[
\text{Area} = \frac{1}{2} \left| 1(5 - 2) + 4(2 - 2) + 7(2 - 5) \right| = \frac{1}{2} \left| 3 + 0 - 21 \right| = \frac{1}{2} \left| -18 \right| = 9
\] -
Calculating the Perimeter of a Rectangle:
Problem: Determine the perimeter of a rectangle with opposite corners at \((2, 3)\) and \((8, 6)\).
- Plot the points and draw the rectangle.
- Identify the lengths of the sides by calculating the differences in the \(x\) and \(y\) coordinates:
- Length of the side parallel to the \(x\)-axis:
- Length of the side parallel to the \(y\)-axis:
- Calculate the perimeter using the formula \( P = 2l + 2w \):
- Thus, the perimeter of the rectangle is \( 18 \) units.
\[
l = |8 - 2| = 6
\]\[
w = |6 - 3| = 3
\]\[
P = 2 \times 6 + 2 \times 3 = 12 + 6 = 18
\] -
Area of an Irregular Polygon:
Problem: Find the area of a polygon with vertices at \((2, 1)\), \((4, 5)\), \((7, 8)\), and \((3, 7)\).
- Plot the points and connect them to form the polygon.
- Use the Shoelace formula to calculate the area:
- Substitute the coordinates into the formula:
- Thus, the area of the irregular polygon is \( 8.5 \) square units.
\[
\text{Area} = \frac{1}{2} \left| x_1y_2 + x_2y_3 + x_3y_4 + x_4y_1 - (y_1x_2 + y_2x_3 + y_3x_4 + y_4x_1) \right|
\]\[
\text{Area} = \frac{1}{2} \left| 2 \cdot 5 + 4 \cdot 8 + 7 \cdot 7 + 3 \cdot 1 - (1 \cdot 4 + 5 \cdot 7 + 8 \cdot 3 + 7 \cdot 2) \right|
\]\[
= \frac{1}{2} \left| 10 + 32 + 49 + 3 - (4 + 35 + 24 + 14) \right| = \frac{1}{2} \left| 94 - 77 \right| = \frac{1}{2} \times 17 = 8.5
\] -
Perimeter of an Irregular Shape:
Problem: Calculate the perimeter of a quadrilateral with vertices at \((1, 1)\), \((5, 1)\), \((6, 4)\), and \((2, 6)\).
- Plot the points and connect them to form the quadrilateral.
- Calculate the distances between consecutive vertices using the distance formula:
- Distance between \((1, 1)\) and \((5, 1)\):
- Distance between \((5, 1)\) and \((6, 4)\):
- Distance between \((6, 4)\) and \((2, 6)\):
- Distance between \((2, 6)\) and \((1, 1)\):
- Sum the distances to find the perimeter:
- The perimeter of the quadrilateral is \( 4 + \sqrt{10} + 2\sqrt{5} + \sqrt{26} \) units.
\[
d_{12} = \sqrt{(5 - 1)^2 + (1 - 1)^2} = \sqrt{16 + 0} = 4
\]\[
d_{23} = \sqrt{(6 - 5)^2 + (4 - 1)^2} = \sqrt{1 + 9} = \sqrt{10}
\]\[
d_{34} = \sqrt{(2 - 6)^2 + (6 - 4)^2} = \sqrt{16 + 4} = \sqrt{20} = 2\sqrt{5}
\]\[
d_{41} = \sqrt{(1 - 2)^2 + (1 - 6)^2} = \sqrt{1 + 25} = \sqrt{26}
\]\[
\text{Perimeter} = 4 + \sqrt{10} + 2\sqrt{5} + \sqrt{26}
\]
These word problems illustrate how to apply the principles of area and perimeter to various shapes on the coordinate plane, enhancing problem-solving skills and practical understanding.

Interactive Tools and Resources
Interactive tools and resources can greatly enhance the understanding of area and perimeter on the coordinate plane. These tools allow for dynamic exploration and visualization of mathematical concepts. Here’s a guide to some of the best interactive tools and resources available:
-
Graphing Calculators:
Graphing calculators enable users to plot points, draw shapes, and calculate area and perimeter on the coordinate plane. Some popular online graphing calculators include:
- Desmos: An intuitive and powerful graphing calculator that allows users to plot functions, points, and shapes. It provides interactive sliders to adjust parameters dynamically.
- GeoGebra: A versatile tool that supports geometry, algebra, and calculus. Users can create and manipulate geometric shapes and visualize their properties.
- Symbolab: Offers advanced features for graphing and solving equations, with a specific focus on step-by-step solutions.
These tools support the visualization and exploration of geometric properties, making it easier to understand area and perimeter calculations.
-
Interactive Geometry Software:
Interactive geometry software allows users to construct and explore geometric figures. Some notable software includes:
- Geometer's Sketchpad: Facilitates the construction and manipulation of geometric shapes, making it ideal for educational purposes.
- Cabri Geometry: Offers tools for constructing and measuring shapes, providing a hands-on approach to learning geometry.
These applications help users develop a deeper understanding of geometric principles through direct manipulation of shapes on the coordinate plane.
-
Educational Websites and Resources:
Numerous websites offer interactive lessons, tutorials, and exercises on area and perimeter. Some valuable resources include:
- Khan Academy: Provides comprehensive lessons on area and perimeter, complete with interactive exercises and quizzes.
- Math is Fun: Features clear explanations and interactive practice problems to reinforce learning.
- IXL: Offers a wide range of interactive problems and immediate feedback to help students master area and perimeter concepts.
These websites provide structured learning paths and practice opportunities to solidify understanding of area and perimeter on the coordinate plane.
-
Interactive Games and Apps:
Games and apps provide a fun and engaging way to practice area and perimeter. Notable options include:
- Math Playground: Features a variety of games focused on geometry, including area and perimeter challenges.
- Prodigy Math Game: Integrates math practice into a role-playing game format, motivating students to learn through play.
- BrainingCamp: Offers interactive simulations and tools to explore geometric concepts, including area and perimeter.
These games and apps make learning math enjoyable, helping users practice and apply their knowledge in a playful context.
-
Online Calculators and Solvers:
Online calculators and solvers can assist with complex area and perimeter problems. Useful tools include:
- CalculatorSoup: Provides online calculators for area and perimeter, including for polygons and irregular shapes.
- Wolfram Alpha: Offers powerful computation capabilities for solving equations and visualizing geometric shapes.
- Mathway: Helps solve area and perimeter problems with step-by-step solutions and explanations.
These online tools are helpful for quickly solving problems and verifying calculations.
Leveraging these interactive tools and resources can enhance understanding and provide practical experience with area and perimeter calculations on the coordinate plane.
Common Mistakes and How to Avoid Them
Calculating area and perimeter on the coordinate plane can be straightforward with practice, but there are several common mistakes that students often make. Here are some of those mistakes and tips on how to avoid them:
-
Mistake 1: Miscounting the Units
When determining the lengths of sides by counting the units on the coordinate grid, students may miscount. Always ensure you start counting from zero and carefully track each unit.
- How to Avoid: Double-check your counts and use a ruler or a straightedge to help guide your counting.
-
Mistake 2: Incorrect Use of the Distance Formula
The distance formula is crucial for finding lengths of sides, especially diagonals. Mistakes often occur in applying the formula \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\).
- How to Avoid: Write down each step clearly and double-check your calculations. Verify the coordinates before substituting them into the formula.
-
Mistake 3: Confusing Perimeter and Area
Students sometimes confuse the formulas and methods for calculating perimeter and area. Remember, perimeter is the total distance around a shape, while area is the amount of space inside it.
- How to Avoid: Memorize and understand the specific formulas for perimeter and area. Use labeled diagrams to help visualize each concept.
-
Mistake 4: Ignoring Units
Another common error is not paying attention to the units used in the problem. This can lead to incorrect interpretations of the results.
- How to Avoid: Always include units in your calculations and final answers. Double-check that your units are consistent throughout the problem.
-
Mistake 5: Incorrectly Dividing Irregular Shapes
When calculating the area of irregular shapes, students may not divide the shape into manageable sections correctly.
- How to Avoid: Practice dividing complex shapes into familiar shapes like rectangles and triangles. Verify that your subdivisions cover the entire shape without overlap or omission.
By being aware of these common mistakes and following the tips to avoid them, you can improve your accuracy in calculating area and perimeter on the coordinate plane.
Let's see an example of using these tips:
Example: Calculating the Perimeter and Area of a Rectangle
Consider a rectangle with vertices at (1, 2), (1, 5), (4, 5), and (4, 2) on the coordinate plane.
- Calculate the side lengths using the distance formula:
- \( \text{Length} = |4 - 1| = 3 \) units
- \( \text{Width} = |5 - 2| = 3 \) units
- Find the perimeter:
- \( \text{Perimeter} = 2 \times ( \text{Length} + \text{Width} ) = 2 \times (3 + 3) = 12 \) units
- Calculate the area:
- \( \text{Area} = \text{Length} \times \text{Width} = 3 \times 3 = 9 \) square units
By following these steps and being mindful of common pitfalls, you can successfully tackle problems involving area and perimeter on the coordinate plane.
Video này giải thích cách tính diện tích và chu vi trên mặt phẳng tọa độ, giúp bạn hiểu rõ hơn về hình học và toán học.
Diện Tích & Chu Vi Trên Mặt Phẳng Tọa Độ | Hình Học | Ăn Pi
READ MORE:
Xem video để hiểu cách tính diện tích và chu vi của các tam giác trên mặt phẳng tọa độ. Hãy tìm hiểu cách sử dụng các công thức và phương pháp tính toán hiệu quả.
Diện tích và Chu vi của Tam giác trên Mặt phẳng Tọa độ