Topic formulas for area perimeter and volume: Welcome to our comprehensive guide on formulas for area, perimeter, and volume. This article will provide you with essential formulas and concepts to solve various geometric problems. Whether you're a student, educator, or professional, you'll find valuable information and practical examples to help you understand and apply these formulas effectively.
Table of Content
- Formulas for Area, Perimeter, and Volume
- Introduction to Area, Perimeter, and Volume
- Fundamental Concepts and Definitions
- Area Formulas for Common Geometric Shapes
- Perimeter Formulas for Common Geometric Shapes
- Volume Formulas for Common Geometric Solids
- Applications of Area, Perimeter, and Volume in Real Life
- How to Choose the Right Formula for Different Problems
- Visual Representations and Diagrams
- Advanced Topics: Calculating Surface Area and Volume for Complex Shapes
- Practical Examples and Step-by-Step Solutions
- Common Mistakes and How to Avoid Them
- Summary and Key Takeaways
- Additional Resources and Further Reading
- YOUTUBE: Xem video về Diện tích, Chu vi, và Thể tích để hiểu rõ hơn về các công thức cơ bản trong toán học.
Formulas for Area, Perimeter, and Volume
This page provides a comprehensive list of formulas for calculating the area, perimeter, and volume of various geometric shapes. Use these formulas to solve problems in geometry and related fields.
Area Formulas
- Square: \( A = s^2 \)
where \( s \) is the length of a side. - Rectangle: \( A = l \times w \)
where \( l \) is the length and \( w \) is the width. - Triangle: \( A = \frac{1}{2} \times b \times h \)
where \( b \) is the base and \( h \) is the height. - Circle: \( A = \pi r^2 \)
where \( r \) is the radius. - Parallelogram: \( A = b \times h \)
where \( b \) is the base and \( h \) is the height. - Trapezoid: \( A = \frac{1}{2} (b_1 + b_2) \times h \)
where \( b_1 \) and \( b_2 \) are the bases and \( h \) is the height.
Perimeter Formulas
- Square: \( P = 4s \)
where \( s \) is the length of a side. - Rectangle: \( P = 2l + 2w \)
where \( l \) is the length and \( w \) is the width. - Triangle: \( P = a + b + c \)
where \( a, b, \) and \( c \) are the lengths of the sides. - Circle (Circumference): \( C = 2\pi r \)
where \( r \) is the radius.
Volume Formulas
- Cube: \( V = s^3 \)
where \( s \) is the length of a side. - Rectangular Prism: \( V = l \times w \times h \)
where \( l \) is the length, \( w \) is the width, and \( h \) is the height. - Cylinder: \( V = \pi r^2 h \)
where \( r \) is the radius and \( h \) is the height. - Sphere: \( V = \frac{4}{3} \pi r^3 \)
where \( r \) is the radius. - Cone: \( V = \frac{1}{3} \pi r^2 h \)
where \( r \) is the radius and \( h \) is the height. - Pyramid: \( V = \frac{1}{3} B \times h \)
where \( B \) is the area of the base and \( h \) is the height.
Table of Common Shapes and Their Formulas
| Shape | Area Formula | Perimeter/Circumference Formula | Volume Formula |
|---|---|---|---|
| Square | \( A = s^2 \) | \( P = 4s \) | N/A |
| Rectangle | \( A = l \times w \) | \( P = 2l + 2w \) | N/A |
| Triangle | \( A = \frac{1}{2} \times b \times h \) | \( P = a + b + c \) | N/A |
| Circle | \( A = \pi r^2 \) | \( C = 2\pi r \) | N/A |
| Cube | N/A | N/A | \( V = s^3 \) |
| Rectangular Prism | N/A | N/A | \( V = l \times w \times h \) |
| Cylinder | N/A | N/A | \( V = \pi r^2 h \) |
| Sphere | N/A | N/A | \( V = \frac{4}{3} \pi r^3 \) |
| Cone | N/A | N/A | \( V = \frac{1}{3} \pi r^2 h \) |
| Pyramid | N/A | N/A | \( V = \frac{1}{3} B \times h \) |
READ MORE:
Introduction to Area, Perimeter, and Volume
Understanding the concepts of area, perimeter, and volume is essential in geometry. These measurements are used to describe the size and extent of various shapes and solids. Let's delve into each concept to build a solid foundation:
- Area: The area is the measure of the space inside a two-dimensional shape. It's expressed in square units (e.g., cm², m²). Common formulas include:
- Rectangle: \( A = l \times w \)
- Triangle: \( A = \frac{1}{2} \times b \times h \)
- Circle: \( A = \pi r^2 \)
- Perimeter: The perimeter is the total distance around the edge of a two-dimensional shape. It's expressed in linear units (e.g., cm, m). Common formulas include:
- Rectangle: \( P = 2(l + w) \)
- Triangle: \( P = a + b + c \)
- Circle (Circumference): \( P = 2\pi r \)
- Volume: The volume measures the space inside a three-dimensional object. It's expressed in cubic units (e.g., cm³, m³). Common formulas include:
- Cube: \( V = a^3 \)
- Rectangular Prism: \( V = l \times w \times h \)
- Cylinder: \( V = \pi r^2 h \)
By mastering these fundamental formulas, you can solve a wide range of problems related to shapes and solids, from simple calculations to more complex applications in real life.
Fundamental Concepts and Definitions
To effectively use the formulas for area, perimeter, and volume, it's crucial to understand some fundamental concepts and definitions. These concepts form the basis of geometric calculations and will help you apply the formulas correctly.
Key Definitions:
- Point: A location in space with no dimensions (length, width, or height).
- Line: A one-dimensional figure that extends infinitely in both directions with no width or height.
- Plane: A flat, two-dimensional surface that extends infinitely in all directions.
- Polygon: A closed figure formed by a finite number of line segments. Common polygons include triangles, rectangles, and squares.
- Circle: A set of points in a plane that are equidistant from a given point called the center.
- Solid: A three-dimensional object with volume. Common solids include cubes, spheres, and cylinders.
Important Concepts:
- Length: A measurement of distance from one point to another. Common units include meters (m) and centimeters (cm).
- Width: A measurement of the extent of an object from side to side.
- Height: A measurement of how tall an object is.
- Base (b): The bottom side of a polygon or the bottom face of a solid.
- Height (h): The perpendicular distance from the base to the topmost point of a shape or solid.
- Radius (r): The distance from the center of a circle to any point on its circumference.
- Diameter (d): The distance across a circle, passing through the center, equal to twice the radius (\( d = 2r \)).
Formulas Recap:
| Shape | Area Formula | Perimeter Formula | Volume Formula |
|---|---|---|---|
| Rectangle | \( A = l \times w \) | \( P = 2(l + w) \) | N/A |
| Triangle | \( A = \frac{1}{2} \times b \times h \) | \( P = a + b + c \) | N/A |
| Circle | \( A = \pi r^2 \) | \( P = 2\pi r \) | N/A |
| Cube | N/A | N/A | \( V = a^3 \) |
| Rectangular Prism | N/A | N/A | \( V = l \times w \times h \) |
| Cylinder | N/A | N/A | \( V = \pi r^2 h \) |
Understanding these fundamental concepts and definitions will help you accurately apply the formulas for area, perimeter, and volume to solve various geometric problems.
Area Formulas for Common Geometric Shapes
Calculating the area of various geometric shapes is a fundamental aspect of geometry. Here are the area formulas for some common shapes:
Rectangle
The area of a rectangle is calculated by multiplying its length (\(l\)) by its width (\(w\)).
Formula: \( A = l \times w \)
Square
The area of a square is found by squaring the length of one of its sides (\(s\)).
Formula: \( A = s^2 \)
Triangle
The area of a triangle is determined by multiplying the base (\(b\)) by the height (\(h\)) and then dividing by 2.
Formula: \( A = \frac{1}{2} \times b \times h \)
Circle
The area of a circle is calculated by multiplying pi (\(\pi\)) by the square of the radius (\(r\)).
Formula: \( A = \pi r^2 \)
Parallelogram
The area of a parallelogram is found by multiplying the base (\(b\)) by the height (\(h\)).
Formula: \( A = b \times h \)
Trapezoid
The area of a trapezoid is calculated by adding the lengths of the two parallel sides (\(a\) and \(b\)), multiplying by the height (\(h\)), and then dividing by 2.
Formula: \( A = \frac{1}{2} \times (a + b) \times h \)
Ellipse
The area of an ellipse is determined by multiplying pi (\(\pi\)), the semi-major axis (\(a\)), and the semi-minor axis (\(b\)).
Formula: \( A = \pi a b \)
Table of Area Formulas
| Shape | Area Formula |
|---|---|
| Rectangle | \( A = l \times w \) |
| Square | \( A = s^2 \) |
| Triangle | \( A = \frac{1}{2} \times b \times h \) |
| Circle | \( A = \pi r^2 \) |
| Parallelogram | \( A = b \times h \) |
| Trapezoid | \( A = \frac{1}{2} \times (a + b) \times h \) |
| Ellipse | \( A = \pi a b \) |
Understanding these area formulas will help you solve various geometric problems efficiently. Practice applying these formulas to different shapes to enhance your skills.
Perimeter Formulas for Common Geometric Shapes
The perimeter of a geometric shape is the total distance around the edge of the shape. Here are the perimeter formulas for some common shapes:
Rectangle
The perimeter of a rectangle is calculated by adding together twice the length (\(l\)) and twice the width (\(w\)).
Formula: \( P = 2l + 2w \) or \( P = 2(l + w) \)
Square
The perimeter of a square is found by multiplying the length of one side (\(s\)) by four.
Formula: \( P = 4s \)
Triangle
The perimeter of a triangle is determined by adding the lengths of all three sides (\(a\), \(b\), and \(c\)).
Formula: \( P = a + b + c \)
Circle (Circumference)
The perimeter of a circle, also known as the circumference, is calculated by multiplying pi (\(\pi\)) by the diameter (\(d\)), or twice the radius (\(r\)).
Formula: \( P = \pi d \) or \( P = 2\pi r \)
Parallelogram
The perimeter of a parallelogram is found by adding twice the base (\(b\)) and twice the side length (\(s\)).
Formula: \( P = 2b + 2s \)
Trapezoid
The perimeter of a trapezoid is calculated by adding the lengths of all four sides (\(a\), \(b\), \(c\), and \(d\)).
Formula: \( P = a + b + c + d \)
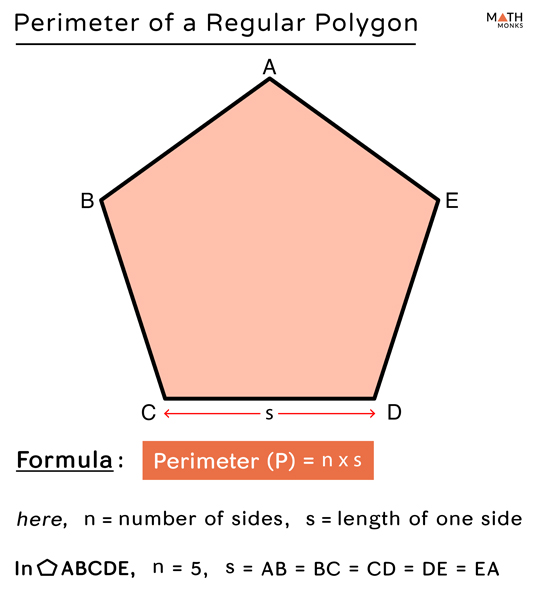
Regular Polygon
The perimeter of a regular polygon (a polygon with all sides and angles equal) is found by multiplying the length of one side (\(s\)) by the number of sides (\(n\)).
Formula: \( P = n \times s \)
Table of Perimeter Formulas
| Shape | Perimeter Formula |
|---|---|
| Rectangle | \( P = 2(l + w) \) |
| Square | \( P = 4s \) |
| Triangle | \( P = a + b + c \) |
| Circle | \( P = 2\pi r \) |
| Parallelogram | \( P = 2b + 2s \) |
| Trapezoid | \( P = a + b + c + d \) |
| Regular Polygon | \( P = n \times s \) |
These perimeter formulas are essential for solving various geometric problems. Practicing these formulas will help you become proficient in calculating the perimeters of different shapes.

Volume Formulas for Common Geometric Solids
Volume is a measure of the amount of space a three-dimensional solid occupies. Here are the volume formulas for some common geometric solids:
Cube
The volume of a cube is found by cubing the length of one of its sides (\(a\)).
Formula: \( V = a^3 \)
Rectangular Prism
The volume of a rectangular prism is calculated by multiplying its length (\(l\)), width (\(w\)), and height (\(h\)).
Formula: \( V = l \times w \times h \)
Sphere
The volume of a sphere is determined by multiplying \(\frac{4}{3}\) by pi (\(\pi\)) and the cube of the radius (\(r\)).
Formula: \( V = \frac{4}{3} \pi r^3 \)
Cylinder
The volume of a cylinder is found by multiplying the area of its base (\(\pi r^2\)) by its height (\(h\)).
Formula: \( V = \pi r^2 h \)
Cone
The volume of a cone is calculated by multiplying \(\frac{1}{3}\) by the area of its base (\(\pi r^2\)) and its height (\(h\)).
Formula: \( V = \frac{1}{3} \pi r^2 h \)
Pyramid
The volume of a pyramid is determined by multiplying \(\frac{1}{3}\) by the area of its base (\(B\)) and its height (\(h\)).
Formula: \( V = \frac{1}{3} B h \)
Table of Volume Formulas
| Solid | Volume Formula |
|---|---|
| Cube | \( V = a^3 \) |
| Rectangular Prism | \( V = l \times w \times h \) |
| Sphere | \( V = \frac{4}{3} \pi r^3 \) |
| Cylinder | \( V = \pi r^2 h \) |
| Cone | \( V = \frac{1}{3} \pi r^2 h \) |
| Pyramid | \( V = \frac{1}{3} B h \) |
Knowing these volume formulas allows you to calculate the space occupied by various three-dimensional solids. Practice using these formulas to enhance your understanding and problem-solving skills in geometry.
Applications of Area, Perimeter, and Volume in Real Life
The concepts of area, perimeter, and volume are not just theoretical; they have numerous practical applications in everyday life. Here are some examples of how these formulas are used in various fields:
Architecture and Construction
- Area: Architects and builders calculate the area of floors, walls, and roofs to determine the amount of materials needed (e.g., tiles, paint).
- Perimeter: The perimeter is used to outline the boundaries of properties, buildings, and rooms, helping to plan fencing and layout.
- Volume: Volume calculations are essential for determining the capacity of spaces, such as rooms, tanks, and swimming pools.
Interior Design
- Area: Interior designers use area calculations to arrange furniture, plan flooring, and select the right amount of carpeting or wallpaper.
- Perimeter: Measuring the perimeter helps in designing trim, moldings, and other decorative elements that run along the edges of spaces.
Gardening and Landscaping
- Area: Gardeners calculate the area of lawns, flower beds, and garden plots to determine the amount of soil, fertilizer, and plants needed.
- Perimeter: Landscaping plans often involve calculating the perimeter for pathways, fencing, and garden borders.
- Volume: Volume is used to calculate the capacity of planters, compost bins, and water features like ponds and fountains.
Sports and Recreation
- Area: Sports fields and courts are designed using area calculations to ensure proper dimensions for playing surfaces.
- Perimeter: The perimeter is important for planning tracks, boundary lines, and fencing around sports facilities.
- Volume: Swimming pools and other recreational facilities require volume calculations to determine water capacity and other materials.
Manufacturing and Packaging
- Area: Manufacturers calculate the area of materials required to produce products, such as fabric for clothing or metal sheets for machinery.
- Perimeter: The perimeter is used in designing labels, packaging, and containers, ensuring proper fit and efficient use of materials.
- Volume: Volume calculations help in designing and producing containers, bottles, and other packaging to ensure they hold the correct amount of product.
Everyday Life
- Area: People use area calculations in home projects, such as painting a room or laying new flooring.
- Perimeter: The perimeter is helpful for tasks like measuring the length of a garden hose needed to water a lawn or determining the amount of trim needed for a room.
- Volume: Volume is used in cooking and baking to measure ingredients and in organizing spaces to determine storage capacity.
These are just a few examples of how area, perimeter, and volume formulas are applied in real life. Understanding and using these concepts can simplify many everyday tasks and professional projects.
How to Choose the Right Formula for Different Problems
Selecting the appropriate formula for calculating area, perimeter, or volume depends on the specific characteristics of the geometric shape or solid in question. Here’s a step-by-step guide to help you choose the right formula for different problems:
1. Identify the Shape or Solid
The first step is to determine the type of geometric shape or solid you are dealing with. Common shapes include rectangles, squares, triangles, and circles, while common solids include cubes, rectangular prisms, spheres, cylinders, cones, and pyramids.
2. Determine What Needs to be Calculated
- Area: If you need to find the amount of space inside a 2D shape, you are calculating the area.
- Perimeter: If you need to find the total distance around the edge of a 2D shape, you are calculating the perimeter.
- Volume: If you need to find the amount of space inside a 3D solid, you are calculating the volume.
3. Use the Appropriate Formula
Once you have identified the shape or solid and determined what needs to be calculated, use the relevant formula from the following tables:
Area Formulas
| Shape | Area Formula |
|---|---|
| Rectangle | \( A = l \times w \) |
| Square | \( A = s^2 \) |
| Triangle | \( A = \frac{1}{2} \times b \times h \) |
| Circle | \( A = \pi r^2 \) |
| Parallelogram | \( A = b \times h \) |
| Trapezoid | \( A = \frac{1}{2} \times (a + b) \times h \) |
| Ellipse | \( A = \pi a b \) |
Perimeter Formulas
| Shape | Perimeter Formula |
|---|---|
| Rectangle | \( P = 2(l + w) \) |
| Square | \( P = 4s \) |
| Triangle | \( P = a + b + c \) |
| Circle (Circumference) | \( P = 2\pi r \) |
| Parallelogram | \( P = 2b + 2s \) |
| Trapezoid | \( P = a + b + c + d \) |
| Regular Polygon | \( P = n \times s \) |
Volume Formulas
| Solid | Volume Formula |
|---|---|
| Cube | \( V = a^3 \) |
| Rectangular Prism | \( V = l \times w \times h \) |
| Sphere | \( V = \frac{4}{3} \pi r^3 \) |
| Cylinder | \( V = \pi r^2 h \) |
| Cone | \( V = \frac{1}{3} \pi r^2 h \) |
| Pyramid | \( V = \frac{1}{3} B h \) |
4. Check Units and Convert if Necessary
Ensure that all measurements are in the same units before applying the formulas. If necessary, convert measurements to the same unit system to maintain consistency.
5. Solve and Verify
Perform the calculations using the chosen formula and verify the results. Double-check your work to ensure accuracy.
By following these steps, you can confidently choose the right formula to solve a variety of geometric problems involving area, perimeter, and volume.
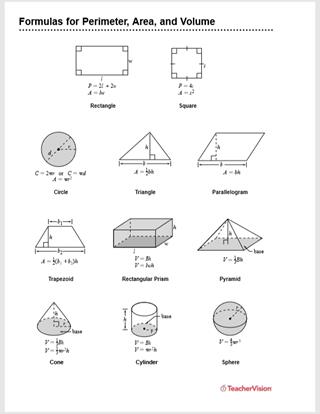
Visual Representations and Diagrams
Visual representations and diagrams are essential tools for understanding and applying formulas for area, perimeter, and volume. They provide a clear and intuitive way to grasp geometric concepts and solve problems effectively. Below are some visual aids for common geometric shapes and solids:
2D Shapes
Rectangle

Formula for Area: \( A = l \times w \)
Formula for Perimeter: \( P = 2(l + w) \)
Square

Formula for Area: \( A = s^2 \)
Formula for Perimeter: \( P = 4s \)
Triangle

Formula for Area: \( A = \frac{1}{2} \times b \times h \)
Formula for Perimeter: \( P = a + b + c \)
Circle

Formula for Area: \( A = \pi r^2 \)
Formula for Circumference: \( C = 2\pi r \)
3D Solids
Cube

Formula for Volume: \( V = a^3 \)
Rectangular Prism

Formula for Volume: \( V = l \times w \times h \)
Sphere

Formula for Volume: \( V = \frac{4}{3} \pi r^3 \)
Cylinder

Formula for Volume: \( V = \pi r^2 h \)
Cone

Formula for Volume: \( V = \frac{1}{3} \pi r^2 h \)
Pyramid

Formula for Volume: \( V = \frac{1}{3} B h \)
Using these visual aids, students and professionals can better understand how to apply the formulas for area, perimeter, and volume to different shapes and solids. Diagrams help in visualizing the dimensions and relationships between different parts of the shapes, making problem-solving more intuitive and effective.

Advanced Topics: Calculating Surface Area and Volume for Complex Shapes
Calculating the surface area and volume for complex shapes involves a deeper understanding of geometric principles and often requires breaking down the shapes into simpler components. Here’s a step-by-step guide to approach these calculations:
1. Decompose the Complex Shape
Begin by breaking down the complex shape into simpler geometric shapes whose surface area and volume formulas are known. For example, a complex solid might be decomposed into a combination of cylinders, spheres, cones, and prisms.
2. Calculate the Surface Area
To find the surface area, calculate the area of each visible face of the decomposed shapes and sum them up. Here are some common formulas:
- Cylinder: \( SA = 2\pi r(h + r) \)
- Sphere: \( SA = 4\pi r^2 \)
- Cone: \( SA = \pi r(r + l) \) where \( l \) is the slant height
- Rectangular Prism: \( SA = 2(lw + lh + wh) \)
3. Calculate the Volume
For volume, calculate the volume of each decomposed shape and sum them up:
- Cylinder: \( V = \pi r^2 h \)
- Sphere: \( V = \frac{4}{3} \pi r^3 \)
- Cone: \( V = \frac{1}{3} \pi r^2 h \)
- Rectangular Prism: \( V = l \times w \times h \)
Example: Composite Shape
Consider a shape that combines a cylinder with a hemisphere on top:
- Decompose the Shape:
- The bottom part is a cylinder.
- The top part is a hemisphere.
- Calculate the Surface Area:
- Cylinder (without top base): \( SA_{cylinder} = 2\pi r h + \pi r^2 \)
- Hemisphere (only curved surface): \( SA_{hemisphere} = 2\pi r^2 \)
- Total Surface Area: \( SA = 2\pi r h + \pi r^2 + 2\pi r^2 = 2\pi r h + 3\pi r^2 \)
- Calculate the Volume:
- Cylinder: \( V_{cylinder} = \pi r^2 h \)
- Hemisphere: \( V_{hemisphere} = \frac{2}{3} \pi r^3 \)
- Total Volume: \( V = \pi r^2 h + \frac{2}{3} \pi r^3 \)
Tips for Complex Shapes
- Use Symmetry: Leverage symmetrical properties to simplify calculations.
- Double-Check Units: Ensure all measurements are in the same units to avoid errors.
- Visualize the Shape: Drawing the shape and its components can help in understanding and breaking it down.
By following these steps, you can effectively calculate the surface area and volume for complex geometric shapes, making it easier to tackle advanced problems in geometry.
Practical Examples and Step-by-Step Solutions
Understanding how to apply the formulas for area, perimeter, and volume is crucial for solving real-life problems. Below are detailed, step-by-step solutions for common geometric shapes.
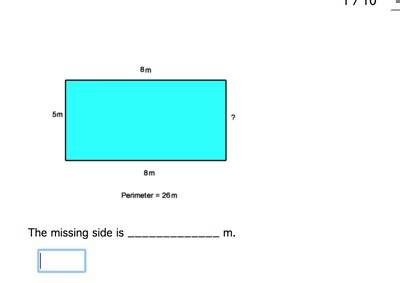
Example 1: Area and Perimeter of a Rectangle
Problem: Find the area and perimeter of a rectangle with a length of 8 meters and a width of 5 meters.
- Identify the formula for the area of a rectangle:
\( \text{Area} = \text{Length} \times \text{Width} \)
- Substitute the given values:
\( \text{Area} = 8 \, \text{m} \times 5 \, \text{m} = 40 \, \text{m}^2 \)
- Identify the formula for the perimeter of a rectangle:
\( \text{Perimeter} = 2 \times (\text{Length} + \text{Width}) \)
- Substitute the given values:
\( \text{Perimeter} = 2 \times (8 \, \text{m} + 5 \, \text{m}) = 2 \times 13 \, \text{m} = 26 \, \text{m} \)
Example 2: Area and Circumference of a Circle
Problem: Find the area and circumference of a circle with a radius of 7 cm.
- Identify the formula for the area of a circle:
\( \text{Area} = \pi r^2 \)
- Substitute the given values:
\( \text{Area} = \pi \times (7 \, \text{cm})^2 = \pi \times 49 \, \text{cm}^2 = 153.94 \, \text{cm}^2 \) (using \( \pi \approx 3.14 \))
- Identify the formula for the circumference of a circle:
\( \text{Circumference} = 2\pi r \)
- Substitute the given values:
\( \text{Circumference} = 2 \pi \times 7 \, \text{cm} = 44 \, \text{cm} \) (using \( \pi \approx 3.14 \))
Example 3: Volume of a Rectangular Prism
Problem: Find the volume of a rectangular prism with a length of 10 cm, a width of 4 cm, and a height of 5 cm.
- Identify the formula for the volume of a rectangular prism:
\( \text{Volume} = \text{Length} \times \text{Width} \times \text{Height} \)
- Substitute the given values:
\( \text{Volume} = 10 \, \text{cm} \times 4 \, \text{cm} \times 5 \, \text{cm} = 200 \, \text{cm}^3 \)
Example 4: Volume of a Cylinder
Problem: Find the volume of a cylinder with a radius of 3 meters and a height of 6 meters.
- Identify the formula for the volume of a cylinder:
\( \text{Volume} = \pi r^2 h \)
- Substitute the given values:
\( \text{Volume} = \pi \times (3 \, \text{m})^2 \times 6 \, \text{m} = \pi \times 9 \, \text{m}^2 \times 6 \, \text{m} = 169.56 \, \text{m}^3 \) (using \( \pi \approx 3.14 \))
Example 5: Area of a Triangle
Problem: Find the area of a triangle with a base of 12 cm and a height of 9 cm.
- Identify the formula for the area of a triangle:
\( \text{Area} = \frac{1}{2} \times \text{Base} \times \text{Height} \)
- Substitute the given values:
\( \text{Area} = \frac{1}{2} \times 12 \, \text{cm} \times 9 \, \text{cm} = 54 \, \text{cm}^2 \)
Practice Problems
Try solving the following problems to test your understanding:
- If a square has an area of 625 sq.m., find its perimeter.
- The length and width of a rectangle are 11.5 cm and 8.8 cm, respectively. Find its area and perimeter.
- If the height of a triangle is 19 cm and its base length is 12 cm, find the area.
- The perimeter of an equilateral triangle is 21 cm. Find its area.
- A parallelogram has a base length of 16 cm and a height of 7.5 cm. Find its area.
Common Mistakes and How to Avoid Them
When working with formulas for area, perimeter, and volume, students and practitioners often encounter common mistakes that can lead to incorrect results. Recognizing these mistakes and understanding how to avoid them is crucial for accurate calculations. Here are some typical errors and tips on how to prevent them:
1. Confusing Perimeter with Area
Perimeter measures the distance around a shape, while area measures the space within the shape. To avoid this confusion:
- Perimeter: Sum of all side lengths. For example, for a rectangle with length \( l \) and width \( w \): \( P = 2l + 2w \).
- Area: Space inside the shape. For a rectangle: \( A = l \times w \).
2. Misapplying Formulas
Using the wrong formula for the shape or dimension can lead to errors. Ensure the correct formula is applied for the specific measurement:
- Circle Area: \( A = \pi r^2 \)
- Circle Circumference: \( C = 2\pi r \)
- Rectangle Volume: \( V = l \times w \times h \)
3. Incorrect Units
Using inconsistent units can cause incorrect calculations. Always ensure that all measurements are in the same units before performing calculations:
- Convert all lengths to the same unit (e.g., all in meters or centimeters).
- Area units will be squared (e.g., cm2, m2).
- Volume units will be cubed (e.g., cm3, m3).
4. Overlooking the Height in Volume Calculations
Volume calculations for 3D shapes often require height, which can be overlooked. Ensure all dimensions are included:
- Volume of a Cylinder: \( V = \pi r^2 h \)
- Volume of a Cone: \( V = \frac{1}{3}\pi r^2 h \)
5. Calculation Errors
Simple arithmetic mistakes can lead to incorrect results. Double-check calculations and consider using tools like calculators or software for complex computations.
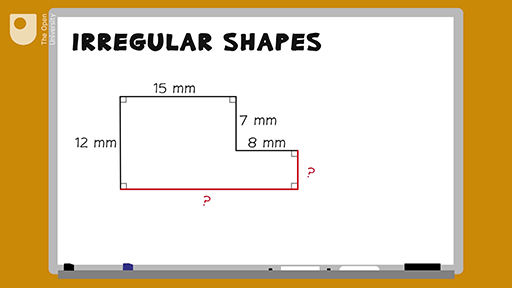
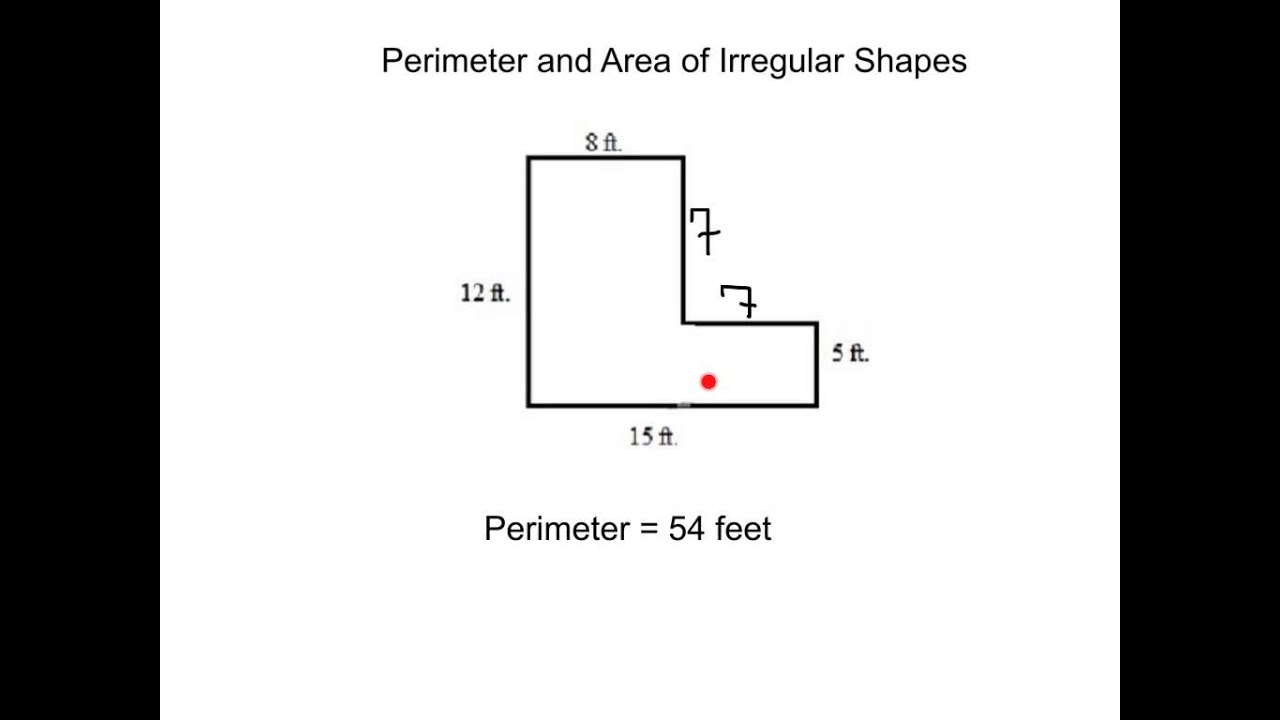
6. Misunderstanding Composite Shapes
For shapes made up of multiple simple shapes, calculate each part separately and then combine the results:
- For composite areas, sum the areas of each part.
- For composite volumes, sum the volumes of each part.
Examples of Common Mistakes and Correct Solutions
-
Problem: Calculating the area of a triangle using the perimeter formula.
Mistake: Using \( P = a + b + c \) instead of \( A = \frac{1}{2} \times base \times height \).
Solution: Use the correct area formula: \( A = \frac{1}{2} \times 5 \times 10 = 25 \) square units.
-
Problem: Mixing units, such as using cm for length and mm for width.
Mistake: Inconsistent units lead to incorrect area or volume.
Solution: Convert all measurements to the same unit before calculating.
-
Problem: Forgetting to include the height in volume calculations for a rectangular prism.
Mistake: Calculating volume as \( l \times w \) instead of \( l \times w \times h \).
Solution: Include all three dimensions: \( V = 2 \times 3 \times 4 = 24 \) cubic units.
By being aware of these common mistakes and understanding how to avoid them, you can ensure more accurate and reliable results in your calculations of area, perimeter, and volume.
Summary and Key Takeaways
Understanding the formulas for calculating area, perimeter, and volume is essential for solving various mathematical and real-world problems. Let's summarize the key points:
- Area formulas provide the measure of space enclosed by a 2-dimensional shape. The area of common geometric shapes like squares, rectangles, triangles, circles, and parallelograms can be calculated using specific formulas.
- Perimeter formulas determine the total length of the boundary of a 2-dimensional shape. Perimeter is crucial for determining fencing requirements, material costs, and more.
- Volume formulas are used to find the amount of space occupied by a 3-dimensional object. These formulas apply to various solid shapes such as cubes, cylinders, spheres, cones, and prisms.
- Applications of area, perimeter, and volume extend beyond the classroom. They are essential in fields like architecture, engineering, construction, and even everyday tasks like gardening or DIY projects.
- Choosing the right formula depends on the given problem and the specific shape involved. Understanding the properties of each shape helps in selecting the appropriate formula for calculation.
- Visual representations, such as diagrams and illustrations, aid in better understanding the concepts and facilitate problem-solving.
- Advanced topics include calculating surface area and volume for complex shapes, which require breaking down the shape into simpler components and applying relevant formulas.
- Practical examples with step-by-step solutions help reinforce understanding and demonstrate the application of formulas in solving real-world problems.
- Avoiding common mistakes, such as miscalculations or misinterpretations of geometric properties, ensures accurate results.
- In conclusion, mastering the formulas for area, perimeter, and volume empowers individuals to tackle a wide range of mathematical and practical challenges effectively.

Additional Resources and Further Reading
For further exploration of formulas for area, perimeter, and volume, consider the following resources:
- : This comprehensive resource provides a wide range of formulas for geometric shapes, along with clear explanations and interactive examples.
- : Khan Academy offers extensive video tutorials and practice exercises covering various geometric concepts, including area, perimeter, and volume.
- : Purplemath offers a collection of formulas, explanations, and tips for mastering geometry concepts, including formulas for area, perimeter, and volume.
- : This resource provides a concise list of formulas for calculating area and perimeter for various geometric shapes, along with example problems.
- : Math Warehouse offers interactive tools, visualizations, and explanations for geometry concepts, including formulas for area, perimeter, and volume.
Xem video về Diện tích, Chu vi, và Thể tích để hiểu rõ hơn về các công thức cơ bản trong toán học.
Diện tích, Chu vi, và Thể tích Giải thích | Toán với Thầy J
READ MORE:
Xem video về Diện tích và Chu vi để tìm hiểu về các khái niệm cơ bản trong toán học.
Diện tích và Chu vi