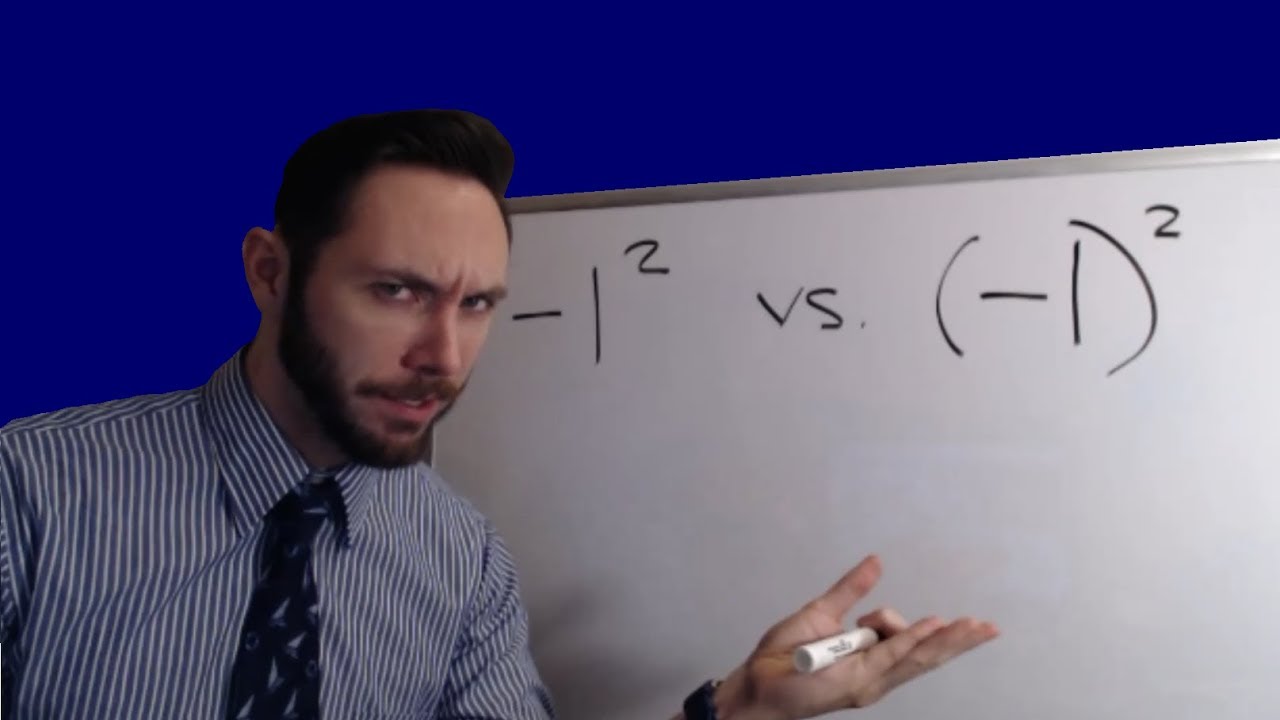How Much is 1 Squared? Discover the Simple Yet Fascinating Answer

The phrase "how much is 1 squared" refers to the mathematical operation of squaring the number 1. Squaring a number means multiplying the number by itself. Here, we will delve into the concept and provide a detailed explanation.

Mathematical Explanation

To find the square of 1, we use the following formula:

\[ 1^2 = 1 \times 1 \]

When we multiply 1 by itself, the result is:

\[ 1 \times 1 = 1 \]

Therefore, the answer to "how much is 1 squared" is:

\[ 1^2 = 1 \]

Applications of Squaring Numbers

Squaring numbers is a fundamental operation in mathematics with various applications in different fields. Some of the key areas include:

• Geometry: Calculating the area of squares.
• Physics: Understanding concepts like acceleration and force.
• Statistics: Working with variance and standard deviation.
• Engineering: Analyzing stress and load on structures.

Visual Representation

Here is a simple visual representation of squaring the number 1:

Conclusion

Understanding how to square a number is essential for grasping more complex mathematical concepts. The result of squaring 1 is straightforward and provides a foundation for learning how to square other numbers.

Squaring a number is one of the most fundamental operations in mathematics. It involves multiplying a number by itself, which is often represented as raising the number to the power of two. This operation is essential for understanding more complex mathematical concepts and has numerous practical applications.

To square a number, you follow these steps:

• Take the number you want to square.
• Multiply the number by itself.
• The result is the squared value of the number.

For example, to square the number 1, we use the following calculation:

\[ 1^2 = 1 \times 1 \]

The result is:

\[ 1^2 = 1 \]

Squaring numbers is a key operation in various fields:

• Geometry: Used to calculate the area of squares, as the area is the side length squared.
• Algebra: Fundamental in solving quadratic equations and understanding parabolas.
• Physics: Essential in formulas involving acceleration and energy, such as kinetic energy where \( E = \frac{1}{2} mv^2 \).
• Statistics: Important for calculating variance and standard deviation, which measure data dispersion.

Understanding the process of squaring numbers helps build a strong foundation in mathematics, enabling the exploration of more advanced topics and practical applications in science and engineering.

The concept of squaring a number is a fundamental arithmetic operation that involves multiplying a number by itself. This operation is often denoted using the exponent 2, indicating that the number is raised to the power of two. Squaring is a crucial building block in various mathematical and scientific applications.

Here’s a step-by-step explanation of how to square a number:

1. Identify the number you wish to square.
2. Multiply the number by itself.
3. The result is the squared value of the number.

For example, to square the number 1, we perform the following calculation:

\[ 1^2 = 1 \times 1 \]

The result is:

\[ 1^2 = 1 \]

Squaring is not only a basic mathematical operation but also has practical significance in various fields:

• Geometry: The area of a square is calculated by squaring the length of its side.
• Algebra: Squaring is used to solve quadratic equations and to work with polynomial expressions.
• Physics: Squaring is involved in formulas for kinetic energy, where the energy depends on the square of the velocity.
• Statistics: Squaring deviations from the mean is part of calculating the variance and standard deviation, which measure data variability.

Understanding the basic concept of squaring is essential for progressing to more advanced mathematical operations and for applying these concepts in practical situations. By mastering squaring, one gains a deeper insight into how numbers and formulas work in everyday applications and scientific studies.

Squaring a number means multiplying the number by itself. The notation for squaring is to use an exponent of 2. For example, squaring the number 1 is written as:

1^2

This means:

Let's break this down step by step:

1. Take the number 1.
2. Multiply it by itself.

In mathematical terms, this is:

1 \times 1 = 1

The result of squaring 1 is therefore:

1^2 = 1

This process holds true for any number. When you square a number, you are essentially finding the area of a square with sides of that length. In the case of 1, it is a square with sides of length 1, which results in an area of:

1 \text{ unit}^2

This simple concept forms the foundation for understanding more complex mathematical principles involving exponents and powers.

Squaring numbers, a fundamental mathematical operation, has numerous applications across various fields. Below are some notable examples:

• Physics: Squaring is used in physics to calculate quantities such as the kinetic energy of an object, which is given by the formula \( E_k = \frac{1}{2}mv^2 \), where \( m \) is the mass and \( v \) is the velocity. The use of squaring in this context helps to describe the energy associated with motion.
• Engineering: In electrical engineering, the power dissipated by a resistor is calculated using the formula \( P = I^2R \), where \( I \) is the current and \( R \) is the resistance. This squared relationship is crucial for designing circuits and managing energy efficiency.
• Statistics: Squaring is fundamental in statistics, particularly in the calculation of variance and standard deviation. Variance is the average of the squared differences from the mean, and it provides a measure of data dispersion.
• Computer Graphics: Squaring functions are used to create smooth shading and realistic lighting effects. For example, the intensity of light at a point on a surface can be determined using squared distance values, enhancing the visual realism in 3D modeling.
• Economics and Finance: Squaring is used in various financial formulas, including the calculation of compound interest and risk assessment models. For instance, the standard deviation of investment returns involves squaring deviations from the mean return.
• Biology and Medicine: In medical imaging, such as MRI scans, the intensity of the images often involves squaring signal values to improve contrast and detail, aiding in better diagnosis and treatment planning.

These applications highlight the versatility and importance of squaring in both theoretical and practical contexts, demonstrating how a simple mathematical operation can have wide-reaching impacts.

Understanding the concept of squaring can be greatly enhanced by visual representations. Squaring a number means multiplying the number by itself. This can be visually demonstrated in various ways:

• Geometric Interpretation:

  Imagine a square with side length \( n \). The area of the square is given by \( n^2 \). For example, if \( n = 1 \), the square has an area of \( 1^2 = 1 \) square unit.

  $1^2$

  Area: 1 square unit

  

• Using Grids:

  Visualize squaring by using a grid. For instance, a 1x1 grid represents \( 1^2 = 1 \). This method is particularly useful for larger numbers, where you can see the square composed of smaller unit squares.

  

• Real-Life Examples:

  Relating squaring to everyday objects can make it easier to grasp. Consider a tile floor where each tile is a square with a side length of 1 foot. One tile would cover an area of \( 1^2 = 1 \) square foot.

  1 foot

  1 foot

These visual aids help solidify the understanding of squaring numbers by providing tangible examples of how the concept applies in both mathematical and real-world contexts.

Understanding the concept of squaring numbers is fundamental in mathematics and has various important applications. Here are some key reasons why mastering this concept is crucial:

• Basic Mathematical Operations: Squaring is one of the simplest forms of exponentiation, where a number is multiplied by itself. For example, 1 squared is 1 (1^2 = 1 \times 1 = 1). This foundational knowledge is essential for understanding more complex mathematical concepts.
• Algebra and Beyond: In algebra, the ability to square numbers is used to solve quadratic equations, work with binomials, and understand polynomial functions. For example, the equation x^2 = 4 has solutions x = 2 and x = -2 because squaring a number always results in a positive number.
• Geometry and Area Calculation: Squaring numbers is directly related to calculating the area of squares. The area of a square is found by squaring the length of its side. For instance, a square with a side length of 1 unit has an area of 1^2 = 1 square unit.
• Physics and Engineering: In physics and engineering, squaring is used in various formulas, including those that calculate energy, force, and other physical properties. For example, the kinetic energy of an object is given by \frac{1}{2}mv^2, where v is the velocity squared.
• Computer Science and Algorithms: Squaring numbers is a common operation in computer science, especially in algorithms that involve optimization, cryptography, and data analysis. Efficient algorithms often rely on mathematical operations like squaring to perform calculations quickly and accurately.
• Statistical Analysis: In statistics, squaring deviations from the mean is a step in calculating variance and standard deviation, which measure the spread of data points. This is critical in fields like data science, economics, and social sciences.
• Real-Life Applications: Squaring numbers is used in real-life scenarios such as calculating areas for construction projects, determining dosages in medicine, and analyzing financial growth patterns. For example, understanding how investments grow over time often involves squaring growth rates.

Overall, a solid grasp of squaring numbers enhances problem-solving skills and analytical thinking, making it a vital mathematical tool across various disciplines.

Understanding the concept of squaring numbers is fundamental in mathematics, but several common misconceptions can lead to confusion. Here are some of the most prevalent misunderstandings:

• Misconception 1: Squaring Always Makes Numbers Larger

  Many people believe that squaring any number will always result in a larger number. While this is true for numbers greater than 1, it does not apply universally. For example, squaring fractions less than 1 results in a smaller number (e.g., \( (\frac{1}{2})^2 = \frac{1}{4} \)), and squaring 1 itself gives 1.

• Misconception 2: Negative Numbers Squared Are Negative

  Another common error is thinking that squaring a negative number results in a negative number. In reality, the square of a negative number is positive because multiplying two negative numbers yields a positive product (e.g., \( (-3)^2 = 9 \)).

• Misconception 3: Confusing Squaring with Multiplication

  Some might confuse squaring a number with simply multiplying it by 2. Squaring a number means multiplying it by itself, not by 2 (e.g., \( 3^2 = 3 \times 3 = 9 \), not \( 3 \times 2 = 6 \)).

• Misconception 4: Zero Squared Is Undefined

  There's a misconception that squaring zero is undefined or problematic. However, zero squared is defined and is simply zero (e.g., \( 0^2 = 0 \)).

• Misconception 5: Squaring Is a Linear Operation

  Some believe that squaring is a linear operation, meaning that the square of a sum is the sum of the squares. This is incorrect, as shown by the distributive property: \( (a + b)^2 \neq a^2 + b^2 \). Instead, \( (a + b)^2 = a^2 + 2ab + b^2 \).

Addressing these misconceptions requires a clear understanding of the fundamental principles of squaring numbers and recognizing the mathematical rules that govern these operations. By clarifying these points, learners can build a more accurate and robust mathematical foundation.

Understanding squaring is not just an abstract mathematical concept; it has numerous practical applications in the real world. Below are some real-world examples where squaring numbers is essential:

• Area Calculation: One of the most common applications of squaring is in calculating the area of squares and rectangles. For example, if the side of a square is 4 meters, the area is calculated as \( 4^2 = 16 \) square meters.
• Physics and Engineering: In physics, the concept of squaring is used in various formulas. For example, the kinetic energy (KE) of an object is given by \( \frac{1}{2} mv^2 \), where \( m \) is the mass and \( v \) is the velocity. Here, the velocity is squared.
• Finance: Squaring is used in financial calculations, such as in the determination of the variance and standard deviation in statistics, which are essential for assessing the risk and volatility of investments. The variance is the average of the squared differences from the mean.
• Computer Graphics: In computer graphics, the distance between two points in a plane can be found using the Pythagorean theorem, which involves squaring the differences in x and y coordinates: \( \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
• Medicine: Dosage calculations in medicine often involve squaring. For instance, the body surface area (BSA), used for determining chemotherapy dosages, is calculated using the square of height and weight in specific formulas.

These examples illustrate that squaring is a fundamental operation with wide-ranging applications that make it an essential concept to understand in both academic and practical contexts.

Understanding the concept of squaring numbers, particularly the example of squaring 1, is fundamental to grasping broader mathematical principles and applications. Here, we reflect on the importance of this simple yet powerful mathematical operation.

• Simplicity and Foundation: The calculation of \(1^2 = 1\) is straightforward, yet it forms the foundation for understanding more complex squaring operations and algebraic concepts. This simplicity helps build confidence in learning and applying mathematics.
• Mathematical Identity: Squaring the number 1 demonstrates the identity property in mathematics, where any number multiplied by 1 remains unchanged. This property is crucial in various proofs and algebraic manipulations.
• Geometric Interpretation: Geometrically, squaring a number relates to finding the area of a square. For 1 squared, this is a 1x1 unit square, emphasizing the basic geometric interpretation of squared values.
• Real-World Applications: Squaring is used extensively in real-world scenarios, such as calculating areas, in physics equations like Einstein’s E=mc², and in statistical formulas such as variance and standard deviation.
• Problem-Solving Skills: Mastery of squaring and understanding its properties enhance problem-solving skills. It encourages logical thinking and the ability to simplify complex problems into manageable parts.
• Preparation for Advanced Topics: A solid grasp of squaring prepares students for advanced mathematical topics, including quadratic equations, polynomial functions, and calculus. It acts as a stepping stone for higher-level math.

In conclusion, the significance of 1 squared lies not only in its simplicity but also in its foundational role in mathematics. It exemplifies core mathematical properties, aids in real-world problem-solving, and paves the way for advanced mathematical learning.