Topic what is x+1 squared: The expression "what is x+1 squared" refers to the mathematical operation of squaring the binomial (x+1), resulting in a quadratic expression. This concept is fundamental in algebra and is widely used in various mathematical applications. Understanding this operation helps in simplifying equations and solving quadratic problems effectively.
Table of Content
- Understanding the Expression (x+1)2
- Introduction
- Definition and Basic Concept
- Step-by-Step Expansion of (x+1) Squared
- Graphical Representation
- Applications in Solving Equations
- Related Algebraic Properties
- Common Mistakes and How to Avoid Them
- Practice Problems and Solutions
- Advanced Topics
- Resources for Further Study
- YOUTUBE: Xem video này để hiểu tại sao 'lũy thừa một nửa của x' tương đương với căn bậc hai và cách áp dụng trong toán học.
Understanding the Expression (x+1)2
The expression (x+1)^2 represents the square of the binomial x+1. This can be expanded and simplified using the distributive property, also known as the FOIL (First, Outer, Inner, Last) method.
Step-by-Step Expansion
Let's break down the expansion of (x+1)^2:
- First: Multiply the first terms in each binomial:
x * x = x^2 - Outer: Multiply the outer terms in the binomials:
x * 1 = x - Inner: Multiply the inner terms in the binomials:
1 * x = x - Last: Multiply the last terms in each binomial:
1 * 1 = 1
Now, combine all these results:
(x+1)^2 = x^2 + x + x + 1 = x^2 + 2x + 1
Mathematical Representation
Using MathJax, the expansion of (x+1)^2 is represented as:
\[(x+1)^2 = x^2 + 2x + 1\]
Applications and Examples
The binomial square formula is a fundamental algebraic identity and is widely used in various mathematical problems. Here are a few applications:
- Solving Quadratic Equations: Helps in factoring and solving quadratic equations.
- Geometry: Used to find the area of squares when the side length is represented as a binomial expression.
- Data Analysis: Essential in statistical formulas like the variance and standard deviation.
Interactive Tools
There are several online tools and calculators that can help you understand and solve such expressions:
Video Explanation
For a visual explanation, you can watch a detailed tutorial on .

READ MORE:
Introduction
When you encounter the expression \((x+1)^2\), it refers to the square of the binomial \(x+1\). This mathematical operation is fundamental in algebra and involves both expansion and simplification processes. Expanding \((x+1)^2\) follows the distributive property and results in a quadratic expression. Understanding this concept is crucial for solving more complex algebraic problems and can be applied in various mathematical contexts.
- Identify the binomial: \((x+1)\).
- Apply the distributive property: \((x+1)(x+1)\).
- Expand the expression:
- \(x \cdot x = x^2\)
- \(x \cdot 1 = x\)
- \(1 \cdot x = x\)
- \(1 \cdot 1 = 1\)
- Combine like terms:
- \(x^2\)
- \(x + x = 2x\)
- \(1\)
- Result: \(x^2 + 2x + 1\)
The final expanded form of \((x+1)^2\) is \(x^2 + 2x + 1\). This process illustrates how algebraic principles are used to simplify and solve equations, providing a foundation for more advanced mathematical operations.
Definition and Basic Concept
The expression \( (x+1)^2 \) represents the square of the binomial \( x+1 \). Squaring a binomial involves multiplying the binomial by itself, which can be expanded using the distributive property, also known as the FOIL (First, Outer, Inner, Last) method.
To understand the expansion step-by-step, consider the binomial \( (x+1) \):
- First: Multiply the first terms of each binomial: \( x \cdot x = x^2 \)
- Outer: Multiply the outer terms: \( x \cdot 1 = x \)
- Inner: Multiply the inner terms: \( 1 \cdot x = x \)
- Last: Multiply the last terms of each binomial: \( 1 \cdot 1 = 1 \)
Combining these results, we get:
| First: | \( x^2 \) |
| Outer: | \( x \) |
| Inner: | \( x \) |
| Last: | \( 1 \) |
Summing these terms, the expanded form of \( (x+1)^2 \) is:
\( x^2 + x + x + 1 \), which simplifies to \( x^2 + 2x + 1 \).
Thus, the squared binomial \( (x+1)^2 \) equals \( x^2 + 2x + 1 \).
Step-by-Step Expansion of (x+1) Squared
Expanding the expression \((x+1)^2\) involves using the distributive property (also known as the FOIL method for binomials) to simplify the expression step by step. Here is a detailed breakdown:
Write the expression as a product of two binomials:
\[(x+1)^2 = (x+1)(x+1)\]
Apply the distributive property (FOIL method):
First: Multiply the first terms in each binomial:
\[x \cdot x = x^2\]
Outside: Multiply the outer terms in the product:
\[x \cdot 1 = x\]
Inside: Multiply the inner terms:
\[1 \cdot x = x\]
Last: Multiply the last terms in each binomial:
\[1 \cdot 1 = 1\]
Add all the products together:
\[x^2 + x + x + 1\]
Combine like terms:
\[x^2 + 2x + 1\]
Thus, the expansion of \((x+1)^2\) results in:
\[x^2 + 2x + 1\]
Graphical Representation
The equation \((x+1)^2\) represents a parabola when graphed on the coordinate plane. Here is a detailed breakdown of how this graph is represented:
- Equation: \((x+1)^2 = x^2 + 2x + 1\)
- Vertex: The vertex of the parabola is at \((-1, 0)\), since shifting the standard parabola \(y = x^2\) one unit to the left aligns with the equation \(y = (x+1)^2\).
- Axis of Symmetry: The axis of symmetry for this parabola is the vertical line \(x = -1\).
- Direction: Since the coefficient of \(x^2\) is positive, the parabola opens upwards.
Graphing this function involves plotting key points and drawing a smooth curve through these points to represent the parabola. Tools like Desmos or graphing calculators can be used to visualize this equation effectively.
| x | y |
| -3 | 4 |
| -2 | 1 |
| -1 | 0 |
| 0 | 1 |
| 1 | 4 |
By plotting these points and connecting them with a smooth curve, you will obtain the graph of \((x+1)^2\), showcasing its parabolic shape with a vertex at \((-1, 0)\) and an axis of symmetry at \(x = -1\).
Applications in Solving Equations
The expression \( (x+1)^2 \) is frequently encountered in algebra and has various applications in solving equations. Below, we explore these applications in detail.
-
Quadratic Equations:
When expanded, \( (x+1)^2 = x^2 + 2x + 1 \). This form is useful for solving quadratic equations. For instance, in the equation \( (x+1)^2 = 9 \), we can solve for \( x \) by first taking the square root of both sides:
- \( (x+1)^2 = 9 \)
- \( x+1 = \pm3 \)
- \( x = 2 \text{ or } x = -4 \)
-
Factoring:
Understanding the square of a binomial helps in factoring complex expressions. For example, knowing \( (x+1)^2 \) allows us to recognize and factor expressions like \( x^2 + 2x + 1 \) back into \( (x+1)^2 \).
-
Inequalities:
In solving inequalities, the squared term \( (x+1)^2 \) can simplify the process. For example, solving \( (x+1)^2 \leq 16 \) involves taking the square root of both sides and solving the resulting inequalities:
- \( (x+1)^2 \leq 16 \)
- \( -4 \leq x+1 \leq 4 \)
- \( -5 \leq x \leq 3 \)
-
Completing the Square:
The process of completing the square often uses \( (x+1)^2 \) to solve quadratic equations. For example, for the equation \( x^2 + 2x + 5 = 0 \), we can rewrite it as \( (x+1)^2 - 1 + 5 = 0 \), which simplifies further to find the roots of the equation.
Related Algebraic Properties
When delving into the realm of algebraic expressions like (x+1) squared, it's essential to understand various related properties that come into play. Here's a breakdown:
- Exponents Rules: These rules govern the manipulation of exponents, crucial for understanding expressions like (x+1) squared. They include the Product Rule, Quotient Rule, and Power Rule.
- Polynomials: (x+1) squared represents a polynomial expression. Understanding the definition of polynomials, their degree, and leading coefficients is fundamental in algebra.
- Factoring Techniques: Knowing how to factor expressions like (x+1) squared can simplify problem-solving. Techniques such as Difference of Squares and Perfect Squares play a significant role here.
Common Mistakes and How to Avoid Them
While dealing with expressions like (x+1) squared, it's common to encounter certain mistakes. Here's how to steer clear of them:
- Incorrect Expansion: One common error is misapplying the distributive property or the FOIL method when expanding (x+1) squared. Always double-check your expansion steps to ensure accuracy.
- Omitting Terms: It's easy to overlook terms or make calculation errors while expanding complex expressions. Take your time and be thorough in each step to avoid omitting crucial terms.
- Confusing with Other Forms: Sometimes, students may confuse (x+1) squared with other algebraic forms, leading to errors in calculations or problem-solving. Practice distinguishing different forms to enhance clarity.
- Forgetting to Simplify: After expanding (x+1) squared, failing to simplify the resulting expression can lead to inaccuracies in further calculations. Always simplify your expressions whenever possible to avoid complications.
Practice Problems and Solutions
Practice makes perfect! Here are some problems related to (x+1) squared along with their solutions:
- Problem 1: Expand (x+1) squared.
- Problem 2: Given the expression x^2 + 2x + 1, factor it.
- Problem 3: Solve the equation (x+1) squared = 16.
| Solution 1: | Using the distributive property, we get: |
| (x+1)(x+1) = x(x) + x(1) + 1(x) + 1(1) = x^2 + x + x + 1 = x^2 + 2x + 1 |
| Solution 2: | Recognizing that x^2 + 2x + 1 is a perfect square trinomial, we factor it as (x+1)(x+1). |
| Solution 3: | By expanding (x+1) squared and setting it equal to 16, we get: |
| x^2 + 2x + 1 = 16 | |
| x^2 + 2x - 15 = 0 | |
| Factoring, we have (x+5)(x-3) = 0. | |
| So, the solutions are x = -5 and x = 3. |
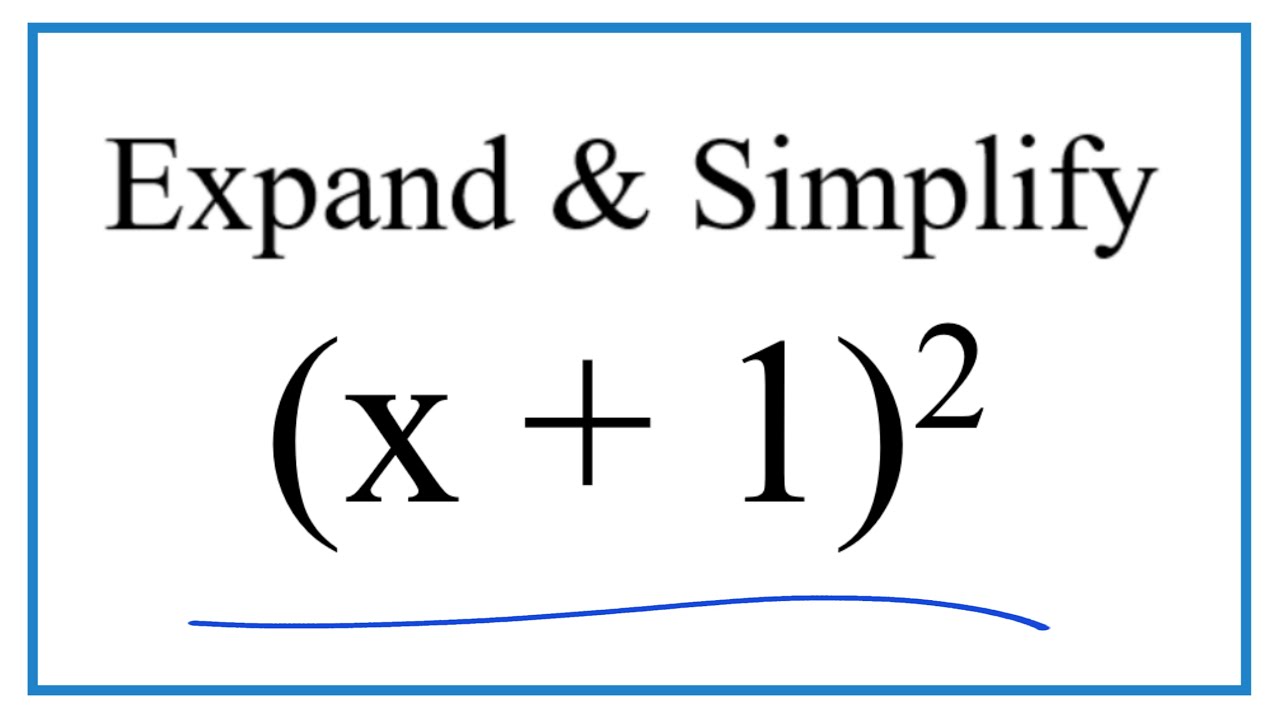
Advanced Topics
Delving deeper into the concept of (x+1) squared opens the door to more advanced topics in mathematics:
- Complex Numbers: Expanding expressions involving (x+1) squared may lead to the introduction of imaginary numbers. Understanding complex numbers and their operations is crucial for tackling more complex algebraic problems.
- Multivariable Calculus: Extending the concept of (x+1) squared to functions of several variables introduces the realm of multivariable calculus. This advanced topic deals with functions of multiple independent variables and their derivatives, integrals, and applications.
Resources for Further Study
Expand your understanding of (x+1) squared with these valuable resources:
- : Dive deeper into quadratic functions and equations, including (x+1) squared, with comprehensive video tutorials and interactive exercises.
- : Explore the world of polynomials, including (x+1) squared, through clear explanations, examples, and interactive activities.
- : Learn how to expand expressions like (x+1) squared step-by-step with detailed explanations and practice problems.
Xem video này để hiểu tại sao 'lũy thừa một nửa của x' tương đương với căn bậc hai và cách áp dụng trong toán học.
Tại sao "lũy thừa một nửa của x" có nghĩa là căn bậc hai?
READ MORE:
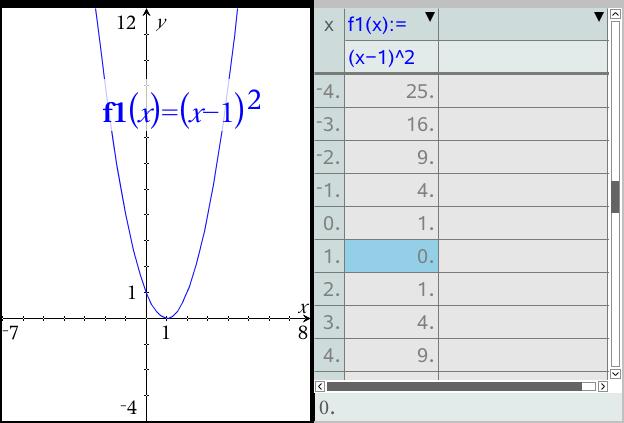
Xem video này để học cách giải các phương trình bình phương của x, như (x-1) ^2 = 0, và áp dụng chúng trong các bài toán toán học thực tế.
Giải phương trình cho các giá trị bình phương của x, ví dụ (x-1) ^2 = 0