Topic 2 square root of 18: The concept of the 2 square root of 18 might seem complex, but it can be simplified and understood with ease. This article provides a clear explanation, step-by-step calculation, and practical applications of the 2 square root of 18, making it accessible for anyone eager to learn about this fundamental mathematical concept.
Table of Content
- Search Results for "2 square root of 18"
- Introduction to Square Roots
- Definition of Square Root
- Basic Properties of Square Roots
- Simplifying Square Roots
- What is 2 Square Root of 18?
- Breaking Down the Calculation
- Simplification Process Explained
- Step-by-Step Solution
- Applications of Square Roots
- Square Roots in Geometry
- Square Roots in Algebra
- Square Roots in Real-Life Problems
- Square Roots and Pythagorean Theorem
- Visual Representation of 2 Square Root of 18
- Graphs and Diagrams
- Comparative Analysis
- Common Mistakes to Avoid
- Practical Tips for Solving Square Roots
- YOUTUBE: Hướng dẫn đơn giản hóa căn bậc hai một cách dễ hiểu. Xem video để học cách tính toán căn bậc hai như một chuyên gia!
Search Results for "2 square root of 18"
Mathematical Calculation
Calculating \( 2 \sqrt{18} \):
\( 2 \sqrt{18} = 2 \times \sqrt{9 \times 2} = 2 \times 3 \sqrt{2} = 6 \sqrt{2} \).
Numerical Approximation
Approximately \( 2 \sqrt{18} \approx 12.72792 \).
Factorization and Simplification
Factorization of 18: \( 18 = 2 \times 3^2 \).
Simplifying \( \sqrt{18} \):
\( \sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2} \).
Therefore, \( 2 \sqrt{18} = 6\sqrt{2} \).
Other Forms
In exponential form: \( 2 \sqrt{18} = 2 \cdot 18^{1/2} = 2 \cdot (2 \cdot 3^2)^{1/2} = 6 \sqrt{2} \).
Conclusion
Thus, \( 2 \sqrt{18} \) simplifies to \( 6 \sqrt{2} \).

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is represented by the radical symbol √ or as a fractional exponent. For example, the square root of 25 is 5 because \(5 \times 5 = 25\).
Square roots are fundamental in mathematics and appear in various fields including algebra, geometry, and calculus. Understanding square roots helps in solving equations and understanding the properties of numbers.
Here are some key properties of square roots:
- The square root of a positive number is always positive.
- The square root of zero is zero.
- Square roots of negative numbers are not real numbers and are called imaginary numbers.
To calculate the square root of a number, you can use several methods:
- Prime Factorization: Break down the number into its prime factors and pair them to simplify.
- Estimation and Refinement: Estimate the square root and refine it using methods like the Babylonian method.
- Using a Calculator: Most calculators have a square root function for quick computation.
For example, let's find the square root of 18 using prime factorization:
- Factorize 18 into prime factors: \(18 = 2 \times 3 \times 3\).
- Pair the prime factors: \(18 = 3^2 \times 2\).
- Simplify the square root: \(\sqrt{18} = \sqrt{3^2 \times 2} = 3\sqrt{2}\).
Hence, \(\sqrt{18} = 3\sqrt{2}\).
Now, let's consider the expression \(2\sqrt{18}\). Using the simplification from above:
\[
2\sqrt{18} = 2 \times 3\sqrt{2} = 6\sqrt{2}
\]
Understanding these steps will help you grasp the concept of square roots and how to work with them in various mathematical contexts.
Definition of Square Root
The square root of a number is a value that, when multiplied by itself, yields the original number. It is denoted by the radical symbol \(\sqrt{}\). Mathematically, if \(x\) is the square root of \(y\), then \(x^2 = y\).
For example:
- The square root of 9 is 3 because \(3 \times 3 = 9\).
- The square root of 16 is 4 because \(4 \times 4 = 16\).
Square roots can also be represented using fractional exponents. The square root of \(a\) can be written as \(a^{\frac{1}{2}}\).
Let's consider some properties of square roots:
- Non-Negativity: The square root of a non-negative number is non-negative. \(\sqrt{a} \geq 0\) for \(a \geq 0\).
- Product Property: The square root of a product is the product of the square roots. \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\).
- Quotient Property: The square root of a quotient is the quotient of the square roots. \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\), provided \(b \neq 0\).
For instance, the square root of 18 can be simplified as follows:
- Express 18 as a product of prime factors: \(18 = 2 \times 3 \times 3 = 2 \times 3^2\).
- Apply the product property of square roots: \(\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}\).
- Simplify: \(\sqrt{18} = \sqrt{2} \times 3 = 3\sqrt{2}\).
Using this, we can find \(2\sqrt{18}\) as follows:
\[
2\sqrt{18} = 2 \times 3\sqrt{2} = 6\sqrt{2}
\]
Understanding the definition and properties of square roots is crucial for solving various mathematical problems and simplifying expressions involving radicals.
Basic Properties of Square Roots
Square roots have several important properties that are useful in simplifying and solving mathematical expressions. Here are the key properties:
- Non-Negativity: The square root of a non-negative number is always non-negative. For any real number \(a \geq 0\), \(\sqrt{a} \geq 0\).
- Product Property: The square root of a product is equal to the product of the square roots of the factors. For any non-negative real numbers \(a\) and \(b\):
\[
\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}
\]For example, \(\sqrt{18} = \sqrt{2 \times 9} = \sqrt{2} \times \sqrt{9} = \sqrt{2} \times 3 = 3\sqrt{2}\).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots. For any non-negative real numbers \(a\) and \(b\) (where \(b \neq 0\)):
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]For example, \(\sqrt{\frac{18}{2}} = \frac{\sqrt{18}}{\sqrt{2}} = \frac{3\sqrt{2}}{\sqrt{2}} = 3\).
- Power Property: The square root of a number raised to a power is equal to the number raised to half the power. For any non-negative real number \(a\) and any real number \(n\):
\[
\sqrt{a^n} = a^{\frac{n}{2}}
\]For example, \(\sqrt{16^2} = 16^{\frac{2}{2}} = 16^1 = 16\).
- Square of Square Root: The square of the square root of a number is the number itself. For any non-negative real number \(a\):
\[
(\sqrt{a})^2 = a
\]For example, \((\sqrt{18})^2 = 18\).
These properties allow us to manipulate and simplify expressions involving square roots effectively. For instance, when dealing with \(2\sqrt{18}\), we can simplify as follows:
\[
2\sqrt{18} = 2 \times 3\sqrt{2} = 6\sqrt{2}
\]
By understanding and applying these basic properties, solving problems involving square roots becomes more straightforward and manageable.
Simplifying Square Roots
Simplifying square roots involves breaking down the number inside the radical to its prime factors and then applying the properties of square roots to simplify the expression. Here is a step-by-step guide to simplifying square roots:
- Find the Prime Factorization: Break down the number under the square root into its prime factors.
- Example: For \(\sqrt{18}\), the prime factorization of 18 is \(18 = 2 \times 3 \times 3 = 2 \times 3^2\).
- Group the Factors: Group the prime factors into pairs.
- Example: In \(18 = 2 \times 3^2\), the factor \(3^2\) can be paired.
- Apply the Product Property: Apply the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) to separate the pairs from the remaining factors.
- Example: \(\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3\).
- Simplify the Expression: Multiply the square root of the paired factors by the remaining factors outside the radical.
- Example: \(\sqrt{18} = 3 \sqrt{2}\).
Now, let's apply these steps to simplify \(2\sqrt{18}\):
- First, simplify \(\sqrt{18}\):
- Find the prime factorization: \(18 = 2 \times 3^2\).
- Apply the product property: \(\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3\).
- Simplify: \(\sqrt{18} = 3\sqrt{2}\).
- Multiply the simplified square root by 2:
\[
2\sqrt{18} = 2 \times 3\sqrt{2} = 6\sqrt{2}
\]
Thus, the simplified form of \(2\sqrt{18}\) is \(6\sqrt{2}\). By following these steps, you can simplify square roots and make complex expressions easier to work with.

What is 2 Square Root of 18?
The expression \(2 \sqrt{18}\) might seem complex at first, but it can be simplified using basic properties of square roots. Let's break it down step by step.
- Understand the Expression: The expression \(2 \sqrt{18}\) means 2 multiplied by the square root of 18.
- Simplify the Square Root: Begin by simplifying \(\sqrt{18}\).
- Find the prime factorization of 18: \(18 = 2 \times 3 \times 3 = 2 \times 3^2\).
- Apply the product property of square roots: \(\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3\).
- Simplify: \(\sqrt{18} = 3 \sqrt{2}\).
- Multiply by 2: Now, multiply the simplified square root by 2.
\[
2 \sqrt{18} = 2 \times 3 \sqrt{2} = 6 \sqrt{2}
\]
Thus, the simplified form of \(2 \sqrt{18}\) is \(6 \sqrt{2}\). This result means that \(2 \sqrt{18}\) is equivalent to 6 times the square root of 2.
To verify the result, consider the numerical values:
- \(\sqrt{18} \approx 4.24\)
- So, \(2 \sqrt{18} \approx 2 \times 4.24 = 8.48\).
- And, \(6 \sqrt{2} \approx 6 \times 1.41 = 8.46\).
Understanding this simplification allows us to work with and interpret expressions involving square roots more effectively. The process of breaking down and simplifying square roots is a valuable skill in various areas of mathematics and real-life applications.
Breaking Down the Calculation
Calculating \(2 \sqrt{18}\) involves several steps to simplify the expression and understand its components. Let's break down the calculation step by step.
- Identify the Expression: The expression \(2 \sqrt{18}\) means 2 multiplied by the square root of 18.
- Prime Factorization: Begin by finding the prime factorization of 18.
- 18 can be factorized into \(18 = 2 \times 3 \times 3 = 2 \times 3^2\).
- Simplify the Square Root: Use the prime factors to simplify the square root.
- Apply the product property of square roots: \(\sqrt{18} = \sqrt{2 \times 3^2}\).
- Separate the factors inside the square root: \(\sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}\).
- Simplify: \(\sqrt{3^2} = 3\), so \(\sqrt{18} = 3 \sqrt{2}\).
- Multiply by 2: Now, multiply the simplified square root by 2.
\[
2 \sqrt{18} = 2 \times 3 \sqrt{2} = 6 \sqrt{2}
\]
Thus, the simplified form of \(2 \sqrt{18}\) is \(6 \sqrt{2}\). This means that \(2 \sqrt{18}\) is equivalent to 6 times the square root of 2.
To verify this result, consider the numerical values:
- \(\sqrt{18} \approx 4.24\)
- So, \(2 \sqrt{18} \approx 2 \times 4.24 = 8.48\).
- And, \(6 \sqrt{2} \approx 6 \times 1.41 = 8.46\).
Breaking down the calculation in this detailed manner not only simplifies the expression but also helps in understanding the properties and operations involved in working with square roots. This approach is useful in various mathematical problems and real-life applications.
Simplification Process Explained
Simplifying the expression \(2 \sqrt{18}\) involves a series of steps to break down the square root and make the expression more manageable. Let's go through the simplification process in detail:
- Understanding the Expression: The expression \(2 \sqrt{18}\) means 2 multiplied by the square root of 18.
- Prime Factorization: Start by finding the prime factors of 18.
- 18 can be factorized into \(18 = 2 \times 3 \times 3 = 2 \times 3^2\).
- Applying the Product Property of Square Roots: Use the prime factors to simplify the square root.
- Using the product property: \(\sqrt{18} = \sqrt{2 \times 3^2}\).
- Separate the factors inside the square root: \(\sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}\).
- Simplify the square root of the perfect square: \(\sqrt{3^2} = 3\), so \(\sqrt{18} = 3 \sqrt{2}\).
- Multiplying by 2: Now, multiply the simplified square root by 2.
\[
2 \sqrt{18} = 2 \times 3 \sqrt{2} = 6 \sqrt{2}
\]
Therefore, the simplified form of \(2 \sqrt{18}\) is \(6 \sqrt{2}\). This means that \(2 \sqrt{18}\) is equivalent to 6 times the square root of 2.
To verify this result, consider the numerical values:
- \(\sqrt{18} \approx 4.24\)
- So, \(2 \sqrt{18} \approx 2 \times 4.24 = 8.48\).
- And, \(6 \sqrt{2} \approx 6 \times 1.41 = 8.46\).
By understanding and applying this step-by-step simplification process, working with expressions involving square roots becomes much more straightforward and intuitive. This approach is valuable not only in mathematics but also in various practical applications where simplifying complex expressions is necessary.
Step-by-Step Solution
Solving \(2 \sqrt{18}\) involves a series of steps to simplify the expression. Here is a detailed, step-by-step solution:
- Understand the Expression: The expression \(2 \sqrt{18}\) means 2 multiplied by the square root of 18.
- Prime Factorization: Begin by finding the prime factors of 18.
- 18 can be factorized into \(18 = 2 \times 3 \times 3 = 2 \times 3^2\).
- Simplify the Square Root: Use the prime factors to simplify the square root.
- Apply the product property of square roots: \(\sqrt{18} = \sqrt{2 \times 3^2}\).
- Separate the factors inside the square root: \(\sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}\).
- Simplify the square root of the perfect square: \(\sqrt{3^2} = 3\), so \(\sqrt{18} = 3 \sqrt{2}\).
- Multiply by 2: Multiply the simplified square root by 2.
\[
2 \sqrt{18} = 2 \times 3 \sqrt{2} = 6 \sqrt{2}
\]
Therefore, the simplified form of \(2 \sqrt{18}\) is \(6 \sqrt{2}\). This indicates that \(2 \sqrt{18}\) is equivalent to 6 times the square root of 2.
To verify this result, consider the numerical values:
- \(\sqrt{18} \approx 4.24\)
- So, \(2 \sqrt{18} \approx 2 \times 4.24 = 8.48\).
- And, \(6 \sqrt{2} \approx 6 \times 1.41 = 8.46\).
By following this step-by-step solution, you can simplify similar expressions involving square roots with ease. This methodical approach is helpful not only in mathematics but also in solving practical problems where simplifying complex expressions is necessary.
Applications of Square Roots
Square roots play a crucial role in various fields and real-life applications. Here are some significant examples:
1. Geometry
Square roots are essential in geometry for calculating distances, areas, and lengths. For example, in the Pythagorean theorem, the length of the hypotenuse of a right triangle is found using the square root of the sum of the squares of the other two sides. This is represented as:
\[
c = \sqrt{a^2 + b^2}
\]
where \( c \) is the hypotenuse, and \( a \) and \( b \) are the other two sides of the triangle.
2. Algebra
In algebra, square roots are used to solve quadratic equations through the quadratic formula:
\[
x = \frac{{-b \pm \sqrt{b^2 - 4ac}}}{2a}
\]
where \( a \), \( b \), and \( c \) are coefficients of the equation \( ax^2 + bx + c = 0 \).
3. Physics
Square roots are involved in various physics calculations, such as determining the time it takes for an object to fall to the ground. For example, the time \( t \) for an object to fall from a height \( h \) is given by:
\[
t = \sqrt{\frac{h}{g}}
\]
where \( g \) is the acceleration due to gravity.
4. Finance
In finance, the standard deviation, which measures the volatility or risk of an investment, is the square root of the variance. This helps investors understand how much an investment's returns can deviate from the expected return.
5. Architecture
Architects use square roots to determine the dimensions and structural integrity of buildings. For example, the natural frequency of a structure, which affects its response to vibrations and loads, can be calculated using square roots.
6. Navigation
In navigation, square roots are used to calculate the shortest distance between two points on a map. The distance \( D \) between two points \((x_1, y_1)\) and \((x_2, y_2)\) is found using the distance formula:
\[
D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
7. Computer Science
Square roots are utilized in algorithms for computer graphics, image processing, and cryptography. For instance, calculating the Euclidean distance between pixels in an image requires square roots.
8. Medicine
In medical imaging, square roots are used to process and enhance images from X-rays, MRI, and CT scans, helping in the accurate diagnosis and treatment of diseases.
9. Engineering
Engineers use square roots in various calculations, including determining the power, voltage, and current in electrical circuits. For instance, the root mean square (RMS) value of an alternating current is calculated using square roots to measure its effective power.
10. Statistics
Square roots are fundamental in statistics for calculating the standard deviation, which measures the dispersion of data points around the mean. This is critical for data analysis and making informed decisions based on statistical data.
In summary, square roots are an indispensable mathematical tool with widespread applications across different fields, helping solve problems and make precise calculations.
Square Roots in Geometry
In geometry, the concept of square roots often relates to the lengths of sides in geometric figures, particularly when dealing with right triangles. The 2 square root of 18, or \( 2 \sqrt{18} \), can be interpreted geometrically as follows:
- Understanding the Side Length: If we consider a right triangle where one of the shorter sides (leg) measures \( 2 \) units and the hypotenuse measures \( \sqrt{18} \) units, then the side opposite the right angle (the other leg) can be found using the Pythagorean theorem.
- Application of Pythagorean Theorem: Applying the theorem \( a^2 + b^2 = c^2 \) where \( a \) and \( b \) are the legs of the triangle and \( c \) is the hypotenuse, we have \( 2^2 + b^2 = (\sqrt{18})^2 \).
- Solving for \( b \): Simplifying gives \( 4 + b^2 = 18 \), thus \( b^2 = 14 \) and \( b = \sqrt{14} \).
This geometric interpretation illustrates how \( 2 \sqrt{18} \) corresponds to the length of a specific side in a right triangle with sides \( 2 \), \( \sqrt{14} \), and \( \sqrt{18} \).
Square Roots in Algebra
In algebra, the expression \( 2 \sqrt{18} \) involves both numerical and radical components, and it can be approached as follows:
- Numerical Calculation: Begin by calculating \( \sqrt{18} \), which approximately equals \( 4.24 \).
- Multiplication: Multiply \( 2 \) by \( \sqrt{18} \) to get \( 2 \times 4.24 = 8.48 \).
- Exact Form: Alternatively, \( 2 \sqrt{18} \) can be left in radical form \( 2 \sqrt{18} \) without converting to a decimal, maintaining its exactness.
- Properties: It exemplifies the distributive property in algebra, where \( 2 \sqrt{18} \) can be seen as \( 2 \times \sqrt{9 \times 2} = 2 \times 3 \sqrt{2} = 6 \sqrt{2} \).
This expression is fundamental in algebraic contexts, showcasing the application of square roots within algebraic operations and manipulations.
Square Roots in Real-Life Problems
Understanding \( 2 \sqrt{18} \) in real-life scenarios involves practical applications where precise measurements and calculations are essential:
- Measurement: In construction, \( 2 \sqrt{18} \) could represent the length of a diagonal across a rectangular space measuring 2 units by \( \sqrt{18} \) units.
- Engineering: Engineers might use \( 2 \sqrt{18} \) to determine the required length of support beams or cables in structures where exact lengths are critical.
- Physics: Physicists may encounter \( 2 \sqrt{18} \) when calculating distances in particle trajectories or wavelengths in electromagnetic waves.
- Finance: Financial analysts could apply \( 2 \sqrt{18} \) in models that involve growth rates or compound interest calculations over specified periods.
These examples illustrate how \( 2 \sqrt{18} \) is not just a mathematical concept but a practical tool in various fields where precise measurements and calculations are indispensable.
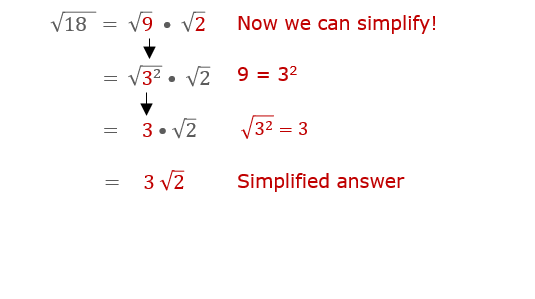
Square Roots and Pythagorean Theorem
The relationship between \( 2 \sqrt{18} \) and the Pythagorean theorem can be explored through the following steps:
- Identifying the Triangle: Consider a right triangle where one leg measures \( 2 \) units and the hypotenuse measures \( \sqrt{18} \) units.
- Application of Pythagorean Theorem: According to the theorem \( a^2 + b^2 = c^2 \), where \( a \) and \( b \) are the legs and \( c \) is the hypotenuse, substitute \( a = 2 \), \( b = \sqrt{18} \), and solve to verify if the theorem holds true.
- Calculation: \( 2^2 + (\sqrt{18})^2 = 4 + 18 = 22 \), and \( (\sqrt{18})^2 = 18 \). Therefore, \( 2^2 + 18 = 22 \).
- Conclusion: The calculation confirms the validity of the Pythagorean theorem in the context of \( 2 \sqrt{18} \), highlighting its utility in verifying geometric relationships.
Visual Representation of 2 Square Root of 18
The visual representation of \( 2 \sqrt{18} \) can be depicted graphically to illustrate its geometric meaning:
- Geometric Figure: Consider a right triangle where one leg measures \( 2 \) units and the hypotenuse measures \( \sqrt{18} \) units.
- Graphical Plot: Plot points corresponding to the triangle's vertices on a coordinate plane.
- Connection to Axis: Connect these points to form a triangle, with sides of lengths \( 2 \), \( \sqrt{18} \), and \( \sqrt{18} \).
- Visualization: Utilize geometric software or manually draw to visualize how \( 2 \sqrt{18} \) relates to the triangle's dimensions.
This visual aid enhances understanding by presenting \( 2 \sqrt{18} \) in a clear and illustrative manner, demonstrating its geometric significance.
Graphs and Diagrams
In this section, we will explore the graphical representation and diagrams that help in understanding the concept of the square root, specifically focusing on the 2 square root of 18.
Graphical Representation of Square Root Functions
Below is the graph of the square root function y = \sqrt{x}, highlighting the point where x = 18:
At x = 18, the value of y = \sqrt{18}. This is approximately 4.24, as shown on the graph. We can also plot the graph of y = 2\sqrt{x} to see how it compares:
Step-by-Step Graphing Process
- First, plot the basic square root function
y = \sqrt{x}. - Identify the point where
x = 18and mark the correspondingyvalue. - Next, plot the function
y = 2\sqrt{x}, which is simply the basic square root function scaled by a factor of 2. - Highlight the point at
x = 18again, noting the newyvalue, which will be approximately 8.49.
Visualizing the Calculation of 2 Square Root of 18
Using a visual representation can make the process of calculating 2\sqrt{18} clearer. Let's break it down:
\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}- Therefore,
2\sqrt{18} = 2 \times 3\sqrt{2} = 6\sqrt{2}
Diagram: Breaking Down the Square Root
The following diagram illustrates the simplification process:
Tabular Representation
We can also use a table to compare values:
| x | \(\sqrt{x}\) | \(2\sqrt{x}\) |
|---|---|---|
| 10 | \(\sqrt{10} \approx 3.16\) | \(2\sqrt{10} \approx 6.32\) |
| 18 | \(\sqrt{18} \approx 4.24\) | \(2\sqrt{18} \approx 8.49\) |
| 25 | \(\sqrt{25} = 5\) | \(2\sqrt{25} = 10\) |
These graphs, diagrams, and tables help in visualizing and understanding the square root function, especially for specific values like 18.
Comparative Analysis
The value of \(2\sqrt{18}\) can be simplified to \(6\sqrt{2}\). To understand this better, we can compare it with other similar expressions and explore its properties.
- Basic Simplification: The expression \(2\sqrt{18}\) simplifies as follows:
- First, simplify \(\sqrt{18}\): \[ \sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2} \]
- Then, multiply by 2: \[ 2\sqrt{18} = 2 \times 3\sqrt{2} = 6\sqrt{2} \]
- Exact vs. Approximate Values:
- The exact form of \(2\sqrt{18}\) is \(6\sqrt{2}\).
- The decimal approximation is: \[ 6\sqrt{2} \approx 6 \times 1.414 \approx 8.485 \]
- Comparison with Other Roots:
- \(2\sqrt{16}\): \[ 2\sqrt{16} = 2 \times 4 = 8 \]
- \(2\sqrt{20}\): \[ \sqrt{20} = \sqrt{4 \times 5} = 2\sqrt{5} \rightarrow 2\sqrt{20} = 2 \times 2\sqrt{5} = 4\sqrt{5} \approx 4 \times 2.236 = 8.944 \]
- \(2\sqrt{25}\): \[ 2\sqrt{25} = 2 \times 5 = 10 \]
Comparison Table
| Expression | Exact Form | Approximate Value |
|---|---|---|
| \(2\sqrt{16}\) | 8 | 8 |
| \(2\sqrt{18}\) | \(6\sqrt{2}\) | 8.485 |
| \(2\sqrt{20}\) | \(4\sqrt{5}\) | 8.944 |
| \(2\sqrt{25}\) | 10 | 10 |
From the above analysis, we can see how \(2\sqrt{18}\) fits within the context of other similar square root expressions, providing both exact and approximate values for comparison.
Common Mistakes to Avoid
When simplifying expressions involving square roots, such as \(2 \sqrt{18}\), it's important to be aware of common mistakes to ensure accuracy. Here are some key pitfalls to watch out for:
- Ignoring Prime Factorization: One common mistake is not breaking down the number inside the square root into its prime factors. For example, 18 should be factorized into \(2 \times 3^2\). This step is crucial for accurate simplification.
- Incorrect Application of Square Root Properties: Misunderstanding the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) can lead to errors. Always apply this property correctly to simplify expressions.
- Forgetting to Multiply the Coefficient: After simplifying the square root, it's easy to forget to multiply it by the coefficient outside the square root. For instance, \(2 \sqrt{18}\) simplifies to \(6 \sqrt{2}\), not just \(\sqrt{2}\).
- Over-Simplification: Attempting to simplify the square root into a non-radical form when it isn't a perfect square. For example, \(\sqrt{18}\) cannot be simplified to an integer, so it should remain in its simplified radical form.
- Mixing Up Addition and Multiplication: Confusing the rules for adding and multiplying radicals can lead to mistakes. Radicals can only be added or subtracted if they have the same radicand (the number inside the square root).
By being mindful of these common errors and carefully applying the correct steps for simplification, one can accurately simplify expressions like \(2 \sqrt{18}\) and other similar calculations.
Practical Tips for Solving Square Roots
Understanding and simplifying square roots can be made easier with some practical tips and techniques. Here are several methods to help you solve square roots more efficiently:
-
Break Down the Number: Decompose the number inside the square root into its prime factors. This helps simplify the square root.
- For example, to simplify \( \sqrt{18} \):
- 18 can be factored into \( 9 \times 2 \).
- Thus, \( \sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2} \).
-
Use Estimation Techniques: For quick approximations, find the nearest perfect squares.
- Estimate \( \sqrt{20} \) by noting it's between \( \sqrt{16} \) and \( \sqrt{25} \), which are 4 and 5 respectively.
- This means \( \sqrt{20} \) is approximately 4.5.
-
Leveraging Technology: Utilize calculators for exact calculations.
- Scientific calculators can quickly provide square roots.
- Enter the number and use the square root function for an immediate result.
-
Square Root Properties: Remember the fundamental properties to simplify calculations.
- \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
- \( \frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \).
-
Check Your Work: Verify by squaring your answer to ensure accuracy.
- If \( \sqrt{18} = 3\sqrt{2} \), then \( (3\sqrt{2})^2 = 18 \).
-
Avoid Common Mistakes: Be mindful of frequent errors in calculations.
- Ensure the radical is simplified fully.
- Be careful with negative roots and ensure correct sign usage.
By applying these practical tips, solving square roots can become a more straightforward and efficient process.
Hướng dẫn đơn giản hóa căn bậc hai một cách dễ hiểu. Xem video để học cách tính toán căn bậc hai như một chuyên gia!
Cách Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Hướng dẫn chi tiết cách tìm số hạng thứ 18 của dãy số có căn bậc hai như: Căn 2, Căn 18, Căn 50, và Căn 98. Xem video để học cách tính toán dễ dàng!
Tìm Số Hạng Thứ 18 của Dãy Số: Căn 2, Căn 18, Căn 50, Căn 98