Topic perimeter equation for triangle: The perimeter equation for a triangle is a fundamental concept in geometry, essential for calculating the total length around a triangle. By summing the lengths of all three sides, one can determine the perimeter. This article explores various triangle types, provides examples, and explains how to use this equation effectively in different scenarios.
Table of Content
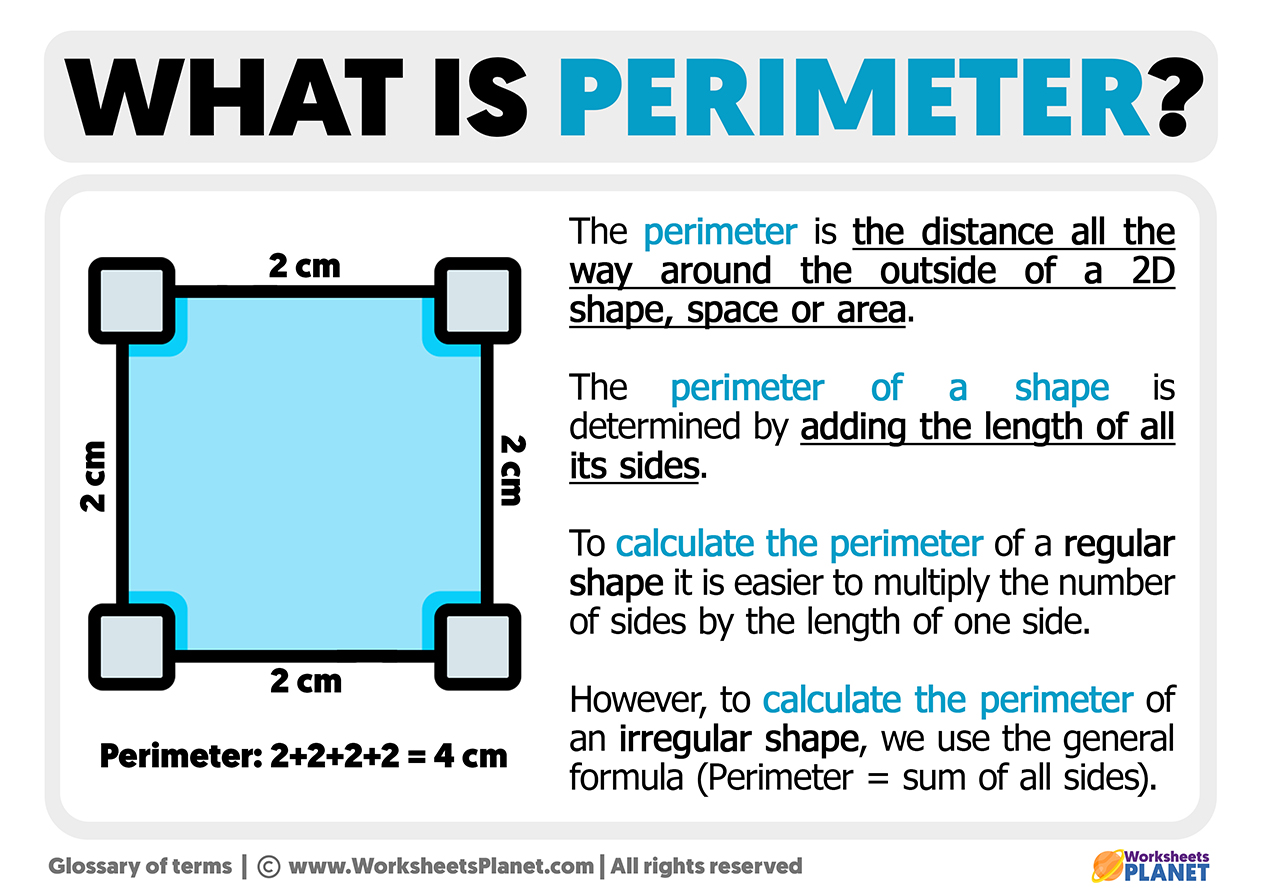
Perimeter of a Triangle
The perimeter of a triangle is the total length of its boundary, which is the sum of the lengths of its three sides. The general formula for the perimeter (P) of a triangle with sides a, b, and c is:
$$ P = a + b + c $$
Special Triangles
- Equilateral Triangle: A triangle with all three sides equal.
$$ P = 3a $$
- Isosceles Triangle: A triangle with two sides equal.
$$ P = 2a + b $$
- Right Triangle: A triangle with one angle equal to 90 degrees.
Using the Pythagorean theorem, if a and b are the legs and c is the hypotenuse:
$$ P = a + b + \sqrt{a^2 + b^2} $$
Examples
- Scalene Triangle:
Find the perimeter of a triangle with sides 6 inches, 8 inches, and 10 inches.
$$ P = 6 + 8 + 10 = 24 \text{ inches} $$
- Right Triangle:
Find the perimeter of a right triangle with legs 4 inches and 3 inches.
First, calculate the hypotenuse:
$$ c = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \text{ inches} $$
Then, the perimeter is:
$$ P = 4 + 3 + 5 = 12 \text{ inches} $$ - Equilateral Triangle:
Find the perimeter of an equilateral triangle with each side measuring 99 inches.
$$ P = 3 \times 99 = 297 \text{ inches} $$
Applications
The perimeter of a triangle is useful in various real-life scenarios such as determining the length of a fence needed to enclose a triangular garden or finding the length of ribbon required to wrap a triangular gift box.
| Type of Triangle | Perimeter Formula |
|---|---|
| Scalene | P = a + b + c |
| Equilateral | P = 3a |
| Isosceles | P = 2a + b |
| Right | P = a + b + √(a² + b²) |

READ MORE:
Introduction
The perimeter of a triangle is a fundamental concept in geometry, representing the total length around the triangle. It is calculated by adding the lengths of all three sides of the triangle. Whether dealing with an equilateral, isosceles, or scalene triangle, understanding how to determine the perimeter is essential for solving various mathematical problems.
For a triangle with side lengths \(a\), \(b\), and \(c\), the perimeter \(P\) is given by:
\[ P = a + b + c \]
Special triangles such as equilateral and isosceles have unique properties that simplify their perimeter calculations:
- Equilateral Triangle: \( P = 3a \)
- Isosceles Triangle: \( P = 2a + b \)
In right triangles, the Pythagorean theorem is often used to find the missing side before calculating the perimeter:
\[ c^2 = a^2 + b^2 \]
Once all sides are known, the perimeter can be found by summing these lengths. This concept is not only foundational in geometry but also has practical applications in various fields such as architecture, engineering, and computer graphics.
Basic Formula for Perimeter
The perimeter of a triangle is the total distance around its three sides. The basic formula to calculate the perimeter is:
\[
\text{Perimeter} = a + b + c
\]
where \(a\), \(b\), and \(c\) are the lengths of the sides of the triangle.
This formula applies to all types of triangles, whether they are scalene, isosceles, or equilateral. Below are specific examples for different types of triangles:
- Equilateral Triangle: All three sides are equal. The formula simplifies to: \[ \text{Perimeter} = 3a \] where \(a\) is the length of one side.
- Isosceles Triangle: Two sides are equal. The formula is: \[ \text{Perimeter} = 2a + b \] where \(a\) is the length of the equal sides and \(b\) is the length of the base.
- Right Triangle: Uses the Pythagorean theorem to find the hypotenuse if it is not known. If the lengths of the legs are \(a\) and \(b\) and the hypotenuse is \(c\), the formula is: \[ \text{Perimeter} = a + b + c \] and \(c\) can be calculated as: \[ c = \sqrt{a^2 + b^2} \]
Understanding these formulas helps in solving various problems related to the perimeter of triangles in geometry.
Perimeter of Special Triangles
The perimeter of a triangle is calculated by summing the lengths of its sides. Special triangles, such as equilateral, isosceles, and right triangles, have unique properties that simplify these calculations.
- Equilateral Triangle: All three sides are equal. If the side length is denoted as \(a\), the perimeter \(P\) is given by:
\[ P = 3a \]
- Isosceles Triangle: Two sides are equal. Let the equal sides be \(a\) and the base be \(b\). The perimeter \(P\) is:
\[ P = 2a + b \]
- Right Triangle: One angle is 90 degrees. The sides are denoted as \(a\) and \(b\) with the hypotenuse \(c\). Using the Pythagorean theorem, the hypotenuse is \(c = \sqrt{a^2 + b^2}\). The perimeter \(P\) is:
\[ P = a + b + \sqrt{a^2 + b^2} \]
Understanding these properties can aid in solving various geometric problems involving triangles.
Isosceles Triangle
An isosceles triangle is a type of triangle that has two sides of equal length, known as the legs, and a third side called the base. This unique structure leads to several interesting properties and formulas.
Properties of Isosceles Triangle
- The two equal sides are called the legs.
- The third side is called the base.
- The angles opposite the equal sides are also equal.
- The sum of all internal angles is always 180 degrees.
Perimeter Formula
The perimeter of an isosceles triangle is calculated by adding the lengths of all three sides. If the lengths of the equal sides are \(a\) and the base is \(b\), the perimeter \(P\) is given by:
\[
P = a + a + b = 2a + b
\]
Examples
Here are a few examples to illustrate the calculation of the perimeter:
-
If the equal sides are 5 cm each and the base is 3 cm, the perimeter is:
\[
P = 2 \times 5 + 3 = 13 \text{ cm}
\] -
Given an isosceles triangle with a perimeter of 30 cm and equal sides of 8 cm each, we can find the base:
\[
30 = 2 \times 8 + b \\
b = 30 - 16 = 14 \text{ cm}
\]
Types of Isosceles Triangles
- Isosceles Acute Triangle: All three angles are less than 90 degrees.
- Isosceles Right Triangle: One of the angles is exactly 90 degrees.
- Isosceles Obtuse Triangle: One of the angles is greater than 90 degrees.

Equilateral Triangle
An equilateral triangle is a special type of triangle where all three sides are of equal length, and each interior angle is 60 degrees. The formula to calculate the perimeter of an equilateral triangle is straightforward since all sides are the same.
To find the perimeter of an equilateral triangle:
- Measure the length of one side of the triangle. Let's denote this length as \(a\).
- Use the formula for the perimeter: \[ \text{Perimeter} = 3a \]
- Multiply the length of one side by 3 to get the total perimeter.
For example, if each side of an equilateral triangle is 7 cm, the perimeter would be calculated as follows:
\[
\text{Perimeter} = 3 \times 7 = 21 \, \text{cm}
\]
This simple formula makes calculating the perimeter of an equilateral triangle very efficient, allowing quick determination of the boundary length of these uniformly sided shapes.
Right Triangle
A right triangle is a type of triangle that has one angle measuring 90 degrees. The side opposite this right angle is the longest side and is called the hypotenuse. The other two sides are known as the legs of the triangle. To find the perimeter of a right triangle, you need the lengths of all three sides. The basic formula for the perimeter \( P \) is:
\[
P = a + b + c
\]
where \( a \) and \( b \) are the lengths of the legs, and \( c \) is the hypotenuse.
To calculate the missing side when only two sides are known, you can use the Pythagorean theorem:
\[
c^2 = a^2 + b^2
\]
For example, if the lengths of the legs \( a \) and \( b \) are known, you can find the hypotenuse \( c \) and then use it to calculate the perimeter:
- Find the hypotenuse using \( c = \sqrt{a^2 + b^2} \).
- Sum all three sides using \( P = a + b + c \).
Consider a right triangle with legs of lengths 3 and 4 units:
- Calculate the hypotenuse: \[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Find the perimeter: \[ P = 3 + 4 + 5 = 12 \]
Therefore, the perimeter of this right triangle is 12 units.
Right triangles are essential in various applications, particularly in trigonometry, where the relationships between their angles and sides form the foundation for many mathematical concepts and real-world applications in fields like engineering and construction.
Conclusion
Calculating the perimeter of a triangle is an essential skill in geometry, providing foundational knowledge that applies to various fields such as architecture, engineering, and everyday problem-solving. The process is straightforward: sum the lengths of all the sides of the triangle. Different types of triangles—scalene, isosceles, equilateral, and right—each have their specific characteristics, but the principle remains the same.
Understanding the perimeter also allows for deeper exploration into other geometric properties and relationships within triangles, such as area, angles, and the application of the Pythagorean theorem in right triangles. Whether dealing with practical applications or theoretical mathematics, mastering the calculation of a triangle's perimeter is a crucial step toward broader mathematical competence.
By familiarizing yourself with the perimeter formulas and practicing with various examples, you will gain confidence and accuracy in your calculations. This knowledge is not only useful academically but also in real-world scenarios where precise measurements and understanding of shapes are required. Keep practicing, and you will find that calculating the perimeter of a triangle becomes second nature.
Làm Thế Nào Để Tìm Chu Vi Của Một Tam Giác
READ MORE:
Làm Thế Nào Để Tìm Chu Vi Của Một Tam Giác | Toán Học với Thầy J