Topic the square root of 16: The square root of 16 is a fundamental concept in mathematics that holds significant importance in various fields. Understanding its properties and applications can provide valuable insights into both basic and advanced mathematical principles. In this article, we explore the methods to calculate it, its properties, and its relevance in real-life scenarios.
Table of Content
- Understanding the Square Root of 16
- Introduction to Square Roots
- Understanding the Concept of Square Roots
- Mathematical Definition of Square Roots
- The Square Root of 16 Explained
- Methods to Calculate the Square Root of 16
- Properties of the Square Root of 16
- Real-Life Applications of Square Roots
- Common Misconceptions About Square Roots
- Advanced Topics Related to Square Roots
- Conclusion
- YOUTUBE: Video này giải thích căn bậc hai của 16 và các ứng dụng của nó trong cuộc sống thực tế. Tìm hiểu cách tính căn bậc hai của 16 và khám phá các ví dụ minh họa.
Understanding the Square Root of 16
The square root of 16 is an essential concept in mathematics, representing a number that, when multiplied by itself, results in 16. This value is commonly taught in basic math courses and can be found using several methods.
Value of the Square Root of 16
The square root of 16 is:
\(\sqrt{16} = \pm 4\)
Since squaring either 4 or -4 gives 16, both are considered the square roots of 16.
Methods to Determine the Square Root of 16
- Prime Factorization Method: By expressing 16 as the product of its prime factors, we get \(16 = 2 \times 2 \times 2 \times 2 = 2^4\). Taking the square root, we have \(\sqrt{16} = \sqrt{(2^2)^2} = 2^2 = 4\).
- Long Division Method: This method involves grouping the digits of 16 from right to left and finding a number which, when squared, results in the given number. For 16, 4 is such a number.
Examples Involving the Square Root of 16
-
Simplify the expression: \( (7\sqrt{16}) + 15 \)
Given: \( (7\sqrt{16}) + 15 \)
Since \(\sqrt{16} = 4\), we substitute this value:
\( 7 \times 4 + 15 = 28 + 15 = 43 \)
-
Find the value of \(m\) if \(m + \sqrt{16} = 20\):
Given: \( m + \sqrt{16} = 20 \)
We know \(\sqrt{16} = 4\), so:
\( m + 4 = 20 \)
Simplifying, \( m = 20 - 4 = 16 \)
FAQs
- Is the square root of 16 a rational number? Yes, since it can be expressed as a fraction \( \frac{4}{1} \).
- Is 16 a perfect square? Yes, because its square root is a whole number.
Table of Roots
| Index | Root Symbol | Value |
|---|---|---|
| 2 | \(\sqrt{16}\) | \(\pm 4\) |
| 3 | \(\sqrt[3]{16}\) | 2.5198420998 |
| 4 | \(\sqrt[4]{16}\) | \(\pm 2\) |

READ MORE:
Introduction to Square Roots
The concept of square roots is a fundamental part of mathematics, essential for understanding various mathematical operations and principles. A square root of a number is a value that, when multiplied by itself, gives the original number. Mathematically, the square root of a number \( x \) is denoted as \( \sqrt{x} \).
For example, the square root of 16 is denoted as \( \sqrt{16} \) and can be calculated as follows:
- \( 4 \times 4 = 16 \)
- Therefore, \( \sqrt{16} = 4 \)
Square roots are applicable in various fields including geometry, algebra, and real-world problem-solving scenarios. Understanding how to calculate and utilize square roots can provide deeper insights into these areas.
Here is a step-by-step method to find the square root of a number:
- Identify the number for which you want to find the square root (e.g., 16).
- Determine which number, when multiplied by itself, equals the original number (e.g., \( 4 \times 4 = 16 \)).
- Express this relationship as the square root (e.g., \( \sqrt{16} = 4 \)).
Square roots also have several important properties:
| Property | Description |
| Non-negative Result | The square root of a non-negative number is always non-negative. |
| Square Root of 0 | The square root of 0 is 0. |
| Square Root of 1 | The square root of 1 is 1. |
| Product Property | \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \) |
| Quotient Property | \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) |
In conclusion, square roots are an essential mathematical tool, aiding in the understanding of various concepts and solving numerous practical problems. Mastering square roots can enhance your mathematical skills and applications.
Understanding the Concept of Square Roots
Square roots are a crucial concept in mathematics, representing a value that, when multiplied by itself, yields the original number. The square root of a number \( x \) is expressed as \( \sqrt{x} \). For example, the square root of 16 is 4 because \( 4 \times 4 = 16 \).
To better understand square roots, consider the following steps and properties:
- Identify the Number: Determine the number for which you want to find the square root (e.g., 16).
- Find the Factor: Determine the number that, when squared, equals the original number. In this case, \( 4 \times 4 = 16 \).
- Express as a Square Root: The relationship is expressed as \( \sqrt{16} = 4 \).
Square roots have several important properties:
| Property | Description |
| Non-negative Result | The square root of a non-negative number is always non-negative. |
| Square Root of 0 | The square root of 0 is 0. |
| Square Root of 1 | The square root of 1 is 1. |
| Product Property | \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \) |
| Quotient Property | \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) |
Square roots also play a vital role in various mathematical fields, such as algebra, geometry, and calculus. They are used to solve equations, simplify expressions, and understand geometric properties.
For instance, in geometry, the square root is essential in calculating the side lengths of squares and the distances between points. In algebra, it helps in solving quadratic equations and simplifying radical expressions. In calculus, understanding square roots is crucial for integrating and differentiating functions involving radicals.
By mastering the concept of square roots, you can enhance your mathematical problem-solving skills and gain deeper insights into various mathematical theories and applications.
Mathematical Definition of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical terms, if x is the square root of y, then x * x = y. This can be written as:
\( x^2 = y \)
The symbol for the square root is √, and it is used to denote the principal (non-negative) square root. For a given number a, the square root is represented as:
\( \sqrt{a} \)
For example, the square root of 16 is written as:
\( \sqrt{16} \)
Using the definition, we find that:
\( 4 \times 4 = 16 \)
Therefore, \( \sqrt{16} = 4 \).
More generally, for any non-negative number a, the square root is a number x such that:
\( x = \sqrt{a} \) and \( x^2 = a \)
Square roots can also be understood through their properties:
- Non-Negative Property: The principal square root of any non-negative number is non-negative.
- Product Property: The square root of a product is the product of the square roots of the factors. For example, \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
- Quotient Property: The square root of a quotient is the quotient of the square roots of the numerator and the denominator. For example, \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \), where \( b \neq 0 \).
- Power Property: The square root of a number raised to the power of two returns the original number. For example, \( \sqrt{a^2} = a \).
These properties help in simplifying complex expressions involving square roots and provide a foundational understanding for further mathematical exploration.
The Square Root of 16 Explained
The square root of a number is a value that, when multiplied by itself, gives the original number. For the number 16, its square root is a value that, when squared, equals 16.
The square root of 16 can be mathematically represented as:
\[\sqrt{16} = 4\]
Here's a detailed step-by-step explanation of how to understand and calculate the square root of 16:
-
Understanding the Basics:
- The square root of a number \( x \) is denoted as \( \sqrt{x} \).
- The operation essentially asks "what number multiplied by itself gives \( x \)?".
-
Square of 4:
- To find the square root of 16, we need to determine what number squared equals 16.
- \[4 \times 4 = 16\]
- Thus, 4 is the square root of 16.
-
Positive and Negative Roots:
- It's important to note that both positive and negative numbers can be square roots.
- For 16, both 4 and -4 are square roots because \((-4) \times (-4) = 16\).
- However, the principal (main) square root is usually taken as the positive value.
-
Verification:
- To verify, simply square the obtained root:
- \[4 \times 4 = 16\]
- \[(-4) \times (-4) = 16\]
- Both calculations confirm that 4 and -4 are indeed the square roots of 16.
-
Visual Representation:
- Graphically, on a number line, the square roots of 16 can be represented as points at +4 and -4.
- This shows the symmetry of positive and negative roots around zero.
In conclusion, the square root of 16 is 4, and understanding this involves recognizing that 4, when squared, gives 16. Additionally, -4 is also a square root of 16, demonstrating the concept of both positive and negative roots.
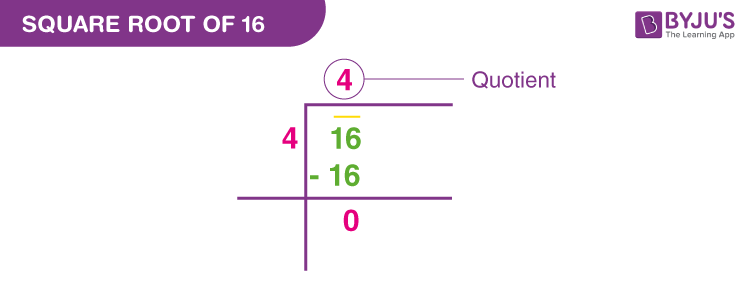
Methods to Calculate the Square Root of 16
There are several methods to calculate the square root of a number. Here, we will explore a few different approaches to find the square root of 16:
-
Prime Factorization Method:
- First, express the number 16 as a product of its prime factors:
- \[16 = 2 \times 2 \times 2 \times 2 = 2^4\]
- To find the square root, take the square root of each factor:
- \[\sqrt{16} = \sqrt{2^4} = 2^{4/2} = 2^2 = 4\]
-
Estimation Method:
- Estimate a number that, when squared, gives a value close to 16.
- We know that \(4 \times 4 = 16\) and \(5 \times 5 = 25\). Since 16 is closer to 4 squared, we can estimate the square root to be 4.
-
Long Division Method:
- This method involves a manual process similar to long division:
- Step 1: Group the digits in pairs, starting from the decimal point.
- Step 2: Find the largest number whose square is less than or equal to the first pair. In this case, 4 since \(4^2 = 16\).
- Step 3: Subtract and bring down the next pair of digits.
- Step 4: Continue the process to get more decimal places if needed. For 16, the square root is exactly 4.
-
Using a Calculator:
- Modern calculators have a square root function, usually denoted by \(\sqrt{}\) or a similar symbol.
- Simply enter the number 16 and press the square root button to get the result:
- \[\sqrt{16} = 4\]
-
Newton's Method (Iterative Approximation):
- Newton's method provides a way to approximate the square root through iteration:
- Start with an initial guess, \( x_0 \). For example, let \( x_0 = 4 \).
- Use the formula: \[x_{n+1} = \frac{1}{2} \left( x_n + \frac{16}{x_n} \right)\]
- After a few iterations, the value converges to 4.
Each of these methods confirms that the square root of 16 is 4. Whether through manual calculation or using tools, the result remains consistent and demonstrates various approaches to understanding square roots.
Properties of the Square Root of 16
The square root of 16, denoted as √16, is a number that, when multiplied by itself, gives the product 16. The properties of the square root of 16 can be understood through various mathematical principles and real-world applications.
Basic Properties
- Value: The square root of 16 is 4, because 4 × 4 = 16.
- Positive and Negative Roots: While the principal square root of 16 is 4, it is important to note that -4 is also a square root of 16, since (-4) × (-4) = 16. Thus, the square roots of 16 are ±4.
- Rational Number: The square root of 16 is a rational number because it can be expressed as the fraction 4/1.
Mathematical Properties
- Exponent Form: The square root of 16 can be written as 161/2 or 160.5.
- Relationship with Exponents: The square root operation is the inverse of squaring. For any positive number \( x \), \( (x^2)^{1/2} = x \).
- Product Property: The square root of a product is the product of the square roots: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \). For example, \( \sqrt{16 \cdot 1} = \sqrt{16} \cdot \sqrt{1} = 4 \cdot 1 = 4 \).
Geometric Interpretation
In geometry, the square root of 16 can be interpreted as the length of the side of a square that has an area of 16 square units.
- Square Area: If a square has an area of 16 square units, each side of the square measures 4 units, since 4 × 4 = 16.
Applications in Real Life
- Measurement: In various measurement scenarios, understanding the square root of 16 can help in determining dimensions. For instance, if a square garden has an area of 16 square meters, each side of the garden is 4 meters long.
- Engineering and Architecture: Engineers and architects frequently use square roots in their calculations, such as determining the side lengths of square plots or components.
Conclusion
Understanding the properties of the square root of 16 enhances our grasp of fundamental mathematical concepts and their applications. Recognizing that 4 and -4 are both roots, that the square root can be expressed in exponential form, and its geometric and real-life relevance, provides a comprehensive view of this important mathematical function.
Real-Life Applications of Square Roots
Square roots are not only fundamental in mathematical theory but also have a wide range of practical applications in various fields. Here are some real-life applications of square roots:
- Engineering: Square roots are used to determine the natural frequency of structures such as bridges and buildings, helping engineers predict how these structures will react to different forces, such as wind or traffic loads.
- Science: Square roots are essential in various scientific calculations. For instance, they are used to calculate the velocity of moving objects, the intensity of sound waves, and the absorption of radiation by materials.
- Statistics: In statistical analysis, square roots are used to calculate standard deviation, a measure that indicates the amount of variation or dispersion in a set of values. This is crucial for interpreting data and making informed decisions.
- Geometry: Square roots are vital in geometry for calculating the area and perimeter of shapes and solving problems involving right triangles using the Pythagorean theorem.
- Computer Science: Square roots are used in algorithms for encryption, image processing, and game physics. For example, encryption algorithms use square roots to generate keys for securing data transmissions.
- Navigation: Pilots and navigators use square roots to calculate the shortest distance between two points on a map or globe, aiding in accurate course plotting.
- Electrical Engineering: Square roots are used to compute power, voltage, and current in electrical circuits, essential for designing and analyzing electrical systems.
- Photography: The aperture of a camera lens, which controls the amount of light entering the camera, is expressed as an f-number. The area of the aperture is proportional to the square of the f-number.
- Accident Investigation: Police use the length of skid marks at accident scenes to calculate the speed of vehicles before braking. This involves evaluating the square root of the product of a constant and the skid distance.
- Cooking: When scaling recipes, especially for large quantities, the square root helps maintain the correct proportions of ingredients, ensuring consistent taste and quality.
- Physics: Square roots are used in formulas that describe physical phenomena, such as the time it takes for an object to fall from a certain height under gravity.
Common Misconceptions About Square Roots
Square roots are often misunderstood, leading to several common misconceptions. Here, we address these misconceptions to help clarify the concept:
-
Misconception 1: The Square Root of a Number Always Has Two Values
Many believe that the square root of a number always results in two values, one positive and one negative. While it's true that a squared number can be positive or negative (e.g., \(5^2 = 25\) and \((-5)^2 = 25\)), the principal square root function, \(\sqrt{x}\), is defined to return only the non-negative value. For example, \(\sqrt{25}\) is 5, not \(\pm 5\).
-
Misconception 2: The Square Root of a Negative Number is Undefined
It's a common belief that you cannot take the square root of a negative number. However, in the realm of complex numbers, the square root of a negative number is defined and involves imaginary units. For instance, \(\sqrt{-16} = 4i\), where \(i\) is the imaginary unit, defined as \(\sqrt{-1}\).
-
Misconception 3: Square Roots and Squaring Are Exact Inverses
Although squaring and square roots are inverse operations, this relationship holds strictly within the domain of non-negative real numbers. When considering all real numbers, the square root function only returns the non-negative value to maintain its status as a function. Hence, \(\sqrt{x^2} = |x|\), not \(\pm x\).
-
Misconception 4: Surds Cannot Be Simplified
Surds, or irrational square roots, can often be simplified. For example, \(\sqrt{45}\) can be simplified to \(3\sqrt{5}\) because 45 has 9 (a perfect square) as a factor. Simplification of surds makes calculations easier and expressions more concise.
-
Misconception 5: Only Perfect Squares Have Square Roots
While it is easier to calculate the square roots of perfect squares (e.g., \(\sqrt{16} = 4\)), non-perfect squares also have square roots, though they are often irrational. For instance, \(\sqrt{10}\) is approximately 3.162, and it does not simplify to a neat integer or fraction.
By understanding and addressing these misconceptions, learners can gain a clearer and more accurate understanding of square roots.
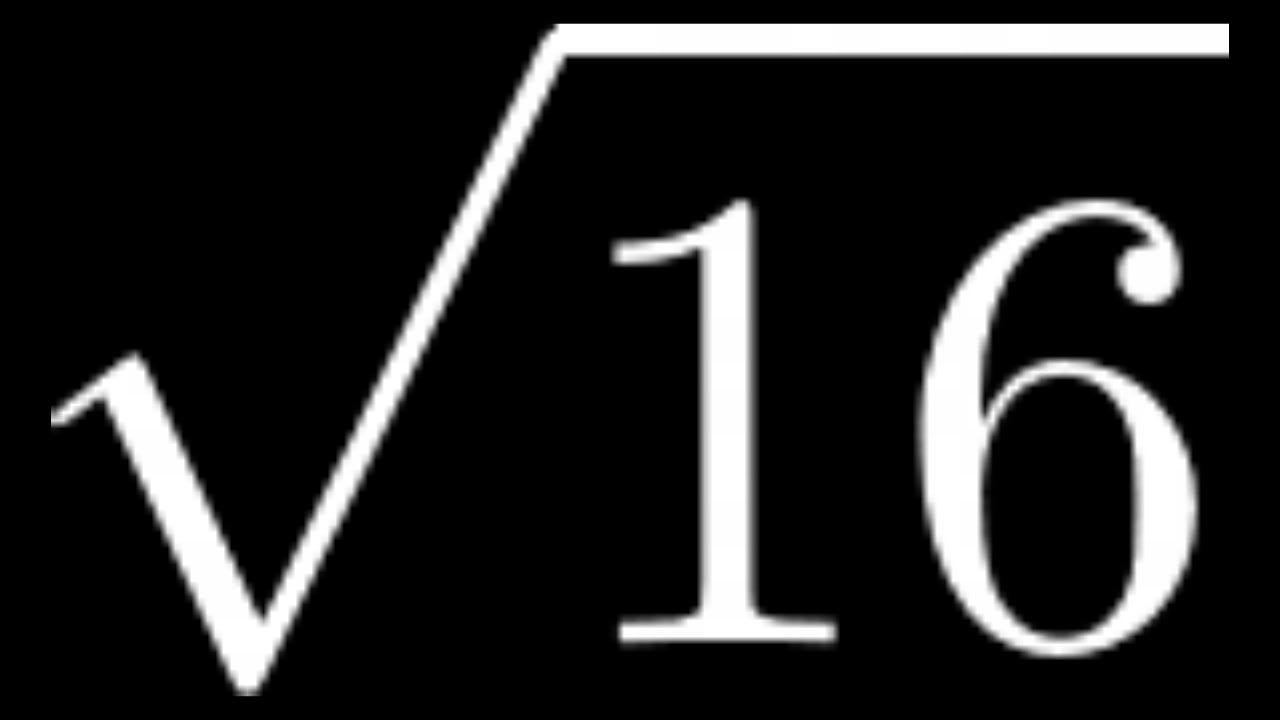
Advanced Topics Related to Square Roots
Exploring square roots further, we can delve into several advanced topics that expand our understanding and application of this fundamental mathematical concept.
1. Square Roots of Negative Numbers and Imaginary Numbers
In the realm of real numbers, the square root of a negative number does not exist. However, in advanced mathematics, we introduce the concept of imaginary numbers. The imaginary unit is denoted as \(i\), where \(i = \sqrt{-1}\). Therefore, the square root of any negative number can be expressed in terms of \(i\).
For example:
\[
\sqrt{-16} = \sqrt{16 \cdot (-1)} = \sqrt{16} \cdot \sqrt{-1} = 4i
\]
2. Complex Numbers
Building on imaginary numbers, we encounter complex numbers. A complex number is of the form \(a + bi\), where \(a\) and \(b\) are real numbers, and \(i\) is the imaginary unit. The square roots of complex numbers involve more intricate calculations and are essential in advanced fields such as electrical engineering and quantum physics.
3. Irrational Numbers
Square roots often result in irrational numbers, which are numbers that cannot be expressed as a simple fraction. These numbers have non-repeating, non-terminating decimal expansions. For example, \(\sqrt{2}\) and \(\sqrt{3}\) are irrational.
Mathematically, we denote these as:
\[
\sqrt{2} \approx 1.414213562 \ldots
\]
\[
\sqrt{3} \approx 1.732050807 \ldots
\]
4. Higher-Order Roots
Beyond square roots, there are higher-order roots such as cube roots (\(\sqrt[3]{x}\)), fourth roots (\(\sqrt[4]{x}\)), and so on. These roots extend the concept of square roots to different dimensions and are used in various complex equations and applications.
For example, the cube root of 8 is:
\[
\sqrt[3]{8} = 2
\]
5. Exponential and Logarithmic Functions
The relationship between roots and powers is fundamental in understanding exponential and logarithmic functions. For any positive number \(x\) and integers \(m\) and \(n\), the following identities hold:
\[
x^{\frac{m}{n}} = \sqrt[n]{x^m} = (\sqrt[n]{x})^m
\]
This relationship is crucial in solving equations involving exponents and logarithms, particularly in calculus and higher-level mathematics.
6. Applications in Geometry
Square roots are extensively used in geometry, especially in calculating distances, areas, and volumes. For instance, the distance \(d\) between two points \((x_1, y_1)\) and \((x_2, y_2)\) in a plane is given by the distance formula, which involves a square root:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
7. Numerical Methods for Finding Square Roots
Various algorithms exist for finding square roots numerically, such as the Newton-Raphson method. This iterative method provides an efficient way to approximate square roots to a high degree of accuracy:
Starting with an initial guess \(x_0\), the formula is:
\[
x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right)
\]
where \(S\) is the number whose square root we seek.
Understanding these advanced topics provides a deeper appreciation of the mathematical elegance and utility of square roots, extending their application to a wide range of scientific and engineering problems.
Conclusion
The square root of 16, which is 4, provides a fascinating glimpse into both fundamental and advanced mathematical concepts. Throughout this guide, we have explored the definition and calculation of square roots, specifically focusing on the square root of 16. We've delved into various methods of finding the square root, such as prime factorization and long division, and have discussed both the theoretical and practical applications of this mathematical operation.
Understanding the square root of 16 not only reinforces basic arithmetic skills but also serves as a stepping stone to more complex topics like irrational numbers and complex roots. It is crucial to grasp these fundamentals as they form the foundation for higher-level math and its applications in fields such as engineering, physics, and computer science.
Furthermore, we examined common misconceptions and advanced topics related to square roots, ensuring a well-rounded comprehension of the subject. By dispelling myths and exploring the properties and nuances of square roots, we can appreciate their importance in mathematical theory and real-world scenarios.
In conclusion, the square root of 16 is a perfect example of how simple mathematical concepts can have wide-reaching implications. Whether you're a student, educator, or math enthusiast, understanding square roots enhances your mathematical literacy and problem-solving abilities. As you continue your mathematical journey, remember that each concept, no matter how basic, contributes to the larger tapestry of knowledge that defines this ever-evolving field.
Video này giải thích căn bậc hai của 16 và các ứng dụng của nó trong cuộc sống thực tế. Tìm hiểu cách tính căn bậc hai của 16 và khám phá các ví dụ minh họa.
Căn Bậc Hai của 16
READ MORE:
Video hướng dẫn cách đơn giản hóa căn bậc hai của 16: sqrt(16). Hãy xem để hiểu rõ hơn và áp dụng cho bài toán của bạn.
Cách Đơn Giản Hóa Căn Bậc Hai Của 16: sqrt(16)













