Topic simplify the square root of 160: Unlock the mystery of simplifying the square root of 160 with our comprehensive guide. Learn the step-by-step process, explore various methods, and understand the mathematical principles behind it. Whether you're a student or a math enthusiast, this article will help you master simplifying square roots with ease and confidence.
Table of Content
- Simplify the Square Root of 160
- Introduction to Simplifying Square Roots
- Steps to Simplify the Square Root of 160
- Alternate Methods
- Prime Factorization Method
- Step-by-Step Simplification Process
- Mathematical Properties of Square Roots
- Square Root of 160 in Decimal Form
- Examples and Practice Problems
- Visual Aids and Diagrams
- Applications of Square Roots in Real Life
- Common Mistakes to Avoid
- Further Reading and Resources
- FAQs on Simplifying Square Roots
- YOUTUBE:
Simplify the Square Root of 160
The process of simplifying the square root of 160 involves factoring the number and then applying the properties of square roots to simplify it. Here's a step-by-step explanation:
Step-by-Step Simplification
- Factor 160 into its prime factors:
160 = 2 × 2 × 2 × 2 × 2 × 5 = 25 × 5
- Group the factors into pairs:
(2 × 2) × (2 × 2) × 2 × 5 = (22) × (22) × 2 × 5
- Take the square root of each pair of factors:
√(22) × √(22) × √(2 × 5)
= 2 × 2 × √(2 × 5)
- Combine the simplified terms:
4√10
Result
The simplified form of the square root of 160 is:
\[\sqrt{160} = 4\sqrt{10}\]
Decimal Form
The decimal approximation of the square root of 160 is:
\[\sqrt{160} \approx 12.649\]
Visual Representation
| Expression | Value |
| \(\sqrt{160}\) | 12.649 |
| \(4\sqrt{10}\) | 12.649 |
This demonstrates that both the radical form \(4\sqrt{10}\) and its decimal approximation 12.649 are equivalent representations of the square root of 160.

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots involves expressing the square root in its simplest form. This process often requires identifying and extracting perfect square factors from the number under the radical sign. The goal is to make the expression easier to work with in mathematical operations.
Steps to Simplify the Square Root of 160
-
Identify Perfect Square Factors: List the factors of 160 and identify the perfect squares. The factors of 160 are 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 80, and 160. The perfect square factors are 1, 4, and 16.
-
Divide by the Largest Perfect Square: Divide 160 by the largest perfect square factor, which is 16. Therefore, 160 ÷ 16 = 10.
-
Calculate the Square Root: Find the square root of the largest perfect square. √16 = 4.
-
Combine Results: Express the simplified form by combining the results from steps 2 and 3. Hence, √160 = 4√10.
Alternate Methods
Other methods for simplifying square roots include prime factorization and approximation techniques such as Newton's method.
Prime Factorization Method
-
Express 160 as a product of prime factors: 160 = 25 × 5.
-
Pair the prime factors to extract perfect squares: √(25 × 5) = 4√10.
Approximation Using Newton's Method
-
Use the formula: √N ≈ ½ (N/A + A), where N is the number and A is an approximation of the square root.
-
For N = 160 and A = 12, the calculation is √160 ≈ ½ (160/12 + 12) ≈ 12.66.
Prime Factorization Method
The prime factorization method is a straightforward and efficient way to simplify square roots by breaking down the number into its prime factors. Here’s how to use this method to simplify the square root of 160.
- Divide the Number into Prime Factors:
Start by dividing 160 by the smallest prime number (which is 2) and continue dividing the quotient by 2 until it is no longer divisible by 2. Then, move on to the next smallest prime number. The prime factorization of 160 is:
160 ÷ 2 = 80 80 ÷ 2 = 40 40 ÷ 2 = 20 20 ÷ 2 = 10 10 ÷ 2 = 5 5 is a prime number. So, the prime factors of 160 are \(2^5 \times 5\).
- Pair the Prime Factors:
Group the prime factors into pairs. In this case, \(2^5 \times 5\) can be grouped as \((2^2 \times 2^2 \times 2 \times 5)\).
- Simplify the Square Root:
Take the square root of each pair and multiply them together. Any unpaired factor will remain inside the square root symbol:
\[
\sqrt{160} = \sqrt{2^5 \times 5} = \sqrt{(2^2 \times 2^2) \times 2 \times 5} = \sqrt{(4 \times 4) \times 2 \times 5} = 4 \times \sqrt{2 \times 5} = 4\sqrt{10}
\]
Thus, the simplified form of \(\sqrt{160}\) is \(4\sqrt{10}\). This method helps break down complex numbers into simpler components, making the process of finding square roots more manageable.
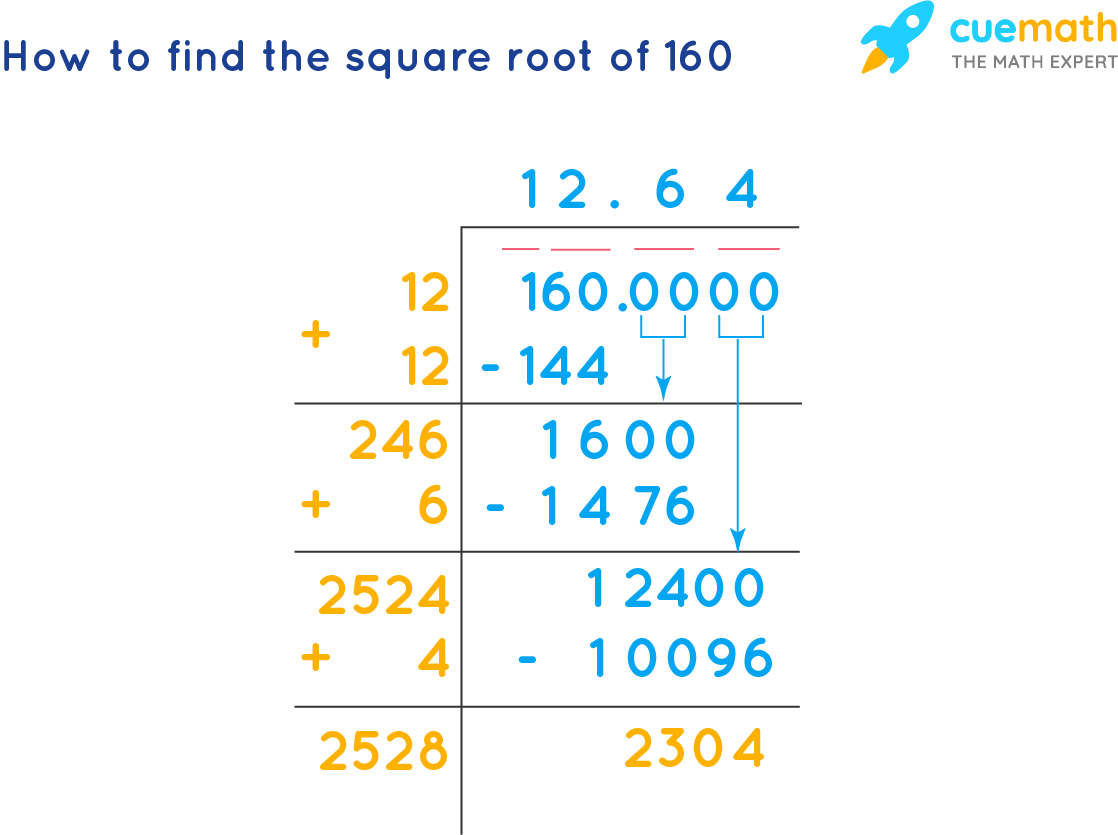
Step-by-Step Simplification Process
To simplify the square root of 160, we use a systematic process involving factorization and simplification. Follow these detailed steps:
- Factorize 160:
Start by finding the prime factors of 160.
- 160 can be factorized as 160 = 2 × 80
- 80 can be factorized as 80 = 2 × 40
- 40 can be factorized as 40 = 2 × 20
- 20 can be factorized as 20 = 2 × 10
- 10 can be factorized as 10 = 2 × 5
So, the prime factorization of 160 is 24 × 5.
- Group the Factors:
Group the factors in pairs of equal factors.
- 24 can be grouped as (2 × 2) × (2 × 2) = 4 × 4
- Apply the Square Root:
Take the square root of each group.
- √(4 × 4 × 5) = √(4) × √(4) × √(5)
- This simplifies to 2 × 2 × √(5)
- Simplify the Expression:
Combine the simplified terms.
- 2 × 2 × √(5) = 4√(5)
Therefore, the square root of 160 in its simplest form is 4√(5).
Mathematical Properties of Square Roots
The properties of square roots are essential for simplifying and understanding radical expressions. Here are some key properties:
Product Property
The product property states that the square root of a product is equal to the product of the square roots of the factors:
- \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\)
For example, \(\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3}\).
Quotient Property
The quotient property states that the square root of a quotient is equal to the quotient of the square roots of the numerator and denominator:
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
For example, \(\sqrt{\frac{16}{4}} = \frac{\sqrt{16}}{\sqrt{4}} = \frac{4}{2} = 2\).
Power Property
The power property states that the square root of a number raised to any power is equal to the number raised to half of that power:
- \(\sqrt{a^n} = a^{n/2}\)
For example, \(\sqrt{25^2} = 25^{2/2} = 25\).
Other Properties
- If a number has a digit in the one's place of 2, 3, 7, or 8, it cannot be a perfect square, and its square root will be irrational.
- The square root of a negative number is considered to be an imaginary value.
These properties are foundational for working with square roots and are useful in various mathematical contexts.
Square Root of 160 in Decimal Form
The square root of 160 is an irrational number, which means it cannot be expressed as an exact fraction and its decimal form is non-repeating and non-terminating. However, we can approximate its value.
In decimal form, the square root of 160 is approximately:
- ± 12.649
This approximation is derived using various methods, such as prime factorization, long division, or Newton's method. Each method helps in breaking down the process to understand how the square root of a non-perfect square can be calculated to a high degree of accuracy.
For practical purposes, the square root of 160 can be rounded to different decimal places based on the required precision:
- To one decimal place: ± 12.6
- To two decimal places: ± 12.65
- To three decimal places: ± 12.649
These values provide a useful approximation for various mathematical and real-world applications where an exact value is not necessary.
Examples and Practice Problems
Practicing simplification of square roots is crucial for mastering algebra. Here are some examples and practice problems to help you get comfortable with the process of simplifying square roots, including the square root of 160.
Let's start with an example:
- Simplify the square root of 160.
- Step 1: Prime factorize 160. The factors are \(160 = 2^5 \times 5\).
- Step 2: Group the prime factors into pairs. In this case, we have \(2^5 = 2^4 \times 2 = (2^2)^2 \times 2 \).
- Step 3: Simplify inside the square root. We can take pairs of numbers out of the square root, so \(\sqrt{160} = \sqrt{(2^2)^2 \times 2 \times 5} = 4\sqrt{10}\).
- Thus, the simplified form of \(\sqrt{160}\) is \(4\sqrt{10}\).
Now, try simplifying these square roots:
- Simplify \(\sqrt{50}\).
- Prime factorize: \(50 = 2 \times 5^2\).
- Simplify: \(\sqrt{50} = \sqrt{2 \times (5^2)} = 5\sqrt{2}\).
- Simplify \(\sqrt{72}\).
- Prime factorize: \(72 = 2^3 \times 3^2\).
- Simplify: \(\sqrt{72} = \sqrt{(2^2) \times (3^2) \times 2} = 6\sqrt{2}\).
- Simplify \(\sqrt{200}\).
- Prime factorize: \(200 = 2^3 \times 5^2\).
- Simplify: \(\sqrt{200} = \sqrt{(2^2) \times (5^2) \times 2} = 10\sqrt{2}\).
These problems will help reinforce your understanding of how to simplify square roots using prime factorization. Practicing these steps will ensure that you can handle any square root simplification with confidence.

Visual Aids and Diagrams
Understanding the process of simplifying the square root of 160 can be made easier with visual aids and diagrams. Below, you will find a detailed breakdown using visual elements to illustrate each step clearly.
Prime Factorization Tree
To simplify the square root of 160, we start with its prime factorization. The following diagram shows the prime factorization tree:
| 160 | ||
| / \ | ||
| 2 80 | ||
| / \ | ||
| 2 40 | ||
| / \ | ||
| 2 20 | ||
| / \ | ||
| 2 10 | ||
| / \ | ||
| 2 5 |
From the prime factorization tree, we get:
\( 160 = 2^5 \times 5 \)
Square Root Simplification Diagram
Next, we simplify the square root of 160 by pairing the factors:
- \( \sqrt{160} = \sqrt{2^5 \times 5} \)
- \( \sqrt{160} = \sqrt{(2^4) \times 2 \times 5} \)
- \( \sqrt{160} = \sqrt{(2^2)^2 \times 2 \times 5} \)
- \( \sqrt{160} = \sqrt{(4)^2 \times 2 \times 5} \)
- \( \sqrt{160} = 4 \times \sqrt{10} \)
Visualization of the Simplified Form
The final simplified form is:
\( \sqrt{160} = 4\sqrt{10} \)
This can be visualized as follows:
|
Original Form: \( \sqrt{160} \) |
Simplified Form: \( 4\sqrt{10} \) |
By understanding the prime factorization and simplification steps, the process becomes clearer, aided by these visual aids and diagrams.
Applications of Square Roots in Real Life
Square roots are fundamental in many real-life applications, ranging from construction and finance to navigation and computer science. Below are some detailed examples:
1. Building Construction
In construction, square roots are essential for determining the lengths of diagonal braces and other angled components to maintain structural integrity. For example, to ensure the correct length of a diagonal brace in a rectangular frame, you can use the Pythagorean theorem:
If the sides of the rectangle are \( a \) and \( b \), the diagonal \( d \) can be found using:
\[
d = \sqrt{a^2 + b^2}
\]
This calculation helps builders to construct accurate and stable structures.
2. Finance
Square roots play a crucial role in finance, especially in calculating the standard deviation and variance, which measure the volatility of stock prices. The standard deviation \( \sigma \) is the square root of the variance \( \sigma^2 \), and it provides insights into the risk associated with an investment:
\[
\sigma = \sqrt{\sigma^2}
\]
Understanding this helps investors make informed decisions.
3. Navigation
In navigation, square roots are used to calculate distances between points. For instance, the distance \( d \) between two points \((x_1, y_1)\) and \((x_2, y_2)\) on a plane can be calculated using:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
This formula is essential for pilots and sailors to determine the most efficient routes.
4. Accident Investigations
Police use square roots to determine the speed of a vehicle before it began to skid. Given the length of the skid marks \( d \), the speed \( s \) can be estimated using:
\[
s = \sqrt{24d}
\]
For example, if the skid marks are 190 feet long, the speed of the car can be approximated as:
\[
s = \sqrt{24 \times 190} \approx 67.5 \text{ mph}
\]
5. Physics
Square roots are used to determine various physical properties, such as the time \( t \) it takes for an object to fall from a height \( h \) due to gravity:
\[
t = \frac{\sqrt{h}}{4}
\]
For example, if an object is dropped from a height of 64 feet, the time to reach the ground is:
\[
t = \frac{\sqrt{64}}{4} = 2 \text{ seconds}
\]
6. Computer Graphics
In computer graphics, calculating distances and rendering 3D models often involve square roots. For instance, the distance between two points in 3D space \((x_1, y_1, z_1)\) and \((x_2, y_2, z_2)\) is given by:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}
\]
This is crucial for realistic rendering and animation in video games and simulations.
7. Electrical Engineering
Electrical engineers use square roots to calculate power, voltage, and current in circuits. For example, the root mean square (RMS) value of an alternating current (AC) is calculated to understand its effective value:
\[
V_{RMS} = \sqrt{\frac{1}{T} \int_0^T [V(t)]^2 dt}
\]
This is vital for designing and analyzing electrical systems.
8. Cooking
In cooking, scaling recipes accurately involves using square roots to maintain the right proportions. If a recipe is scaled by a factor \( f \), the amount of each ingredient should be multiplied by the square root of \( f \) to maintain the balance of flavors:
\[
\text{New Amount} = \text{Original Amount} \times \sqrt{f}
\]
Conclusion
Square roots are indispensable in various fields, providing critical solutions to problems in construction, finance, navigation, physics, computer graphics, electrical engineering, and even cooking. Understanding and applying square roots allows for precise calculations and informed decision-making in many aspects of life.
Common Mistakes to Avoid
Simplifying square roots can be straightforward, but several common mistakes can complicate the process. Being aware of these pitfalls helps ensure accurate and efficient simplification.
-
Overlooking Perfect Squares:
Always check for perfect squares within the radicand (the number under the square root). For example, in √160, recognize that 16 is a perfect square, making it easier to simplify √160 to 4√10.
-
Incorrect Application of Properties:
Misapplying properties like assuming √(a + b) = √a + √b is a common error. Remember, properties like √(ab) = √a * √b only apply to multiplication and division, not addition or subtraction.
-
Ignoring Prime Factorization:
Prime factorization helps break down the radicand into simpler parts. For √160, the prime factorization is 2^5 * 5. Identifying these factors allows you to simplify the square root effectively.
-
Skipping Steps in Simplification:
Rushing through the simplification process can lead to errors. Break down the steps: factorize the radicand, separate perfect squares, and simplify systematically.
-
Neglecting to Rationalize the Denominator:
Leaving a square root in the denominator is often considered incomplete. Rationalize the denominator to simplify the expression fully. For example, rationalize 1/√2 to √2/2.
-
Arithmetic Errors:
Careless arithmetic mistakes, such as incorrect multiplication or division, can lead to wrong results. Double-check your calculations at each step to avoid such errors.
By avoiding these common mistakes, you can simplify square roots more accurately and efficiently, enhancing your overall mathematical proficiency.
Further Reading and Resources
For those looking to delve deeper into the topic of simplifying square roots, particularly the square root of 160, here are some valuable resources that offer comprehensive explanations, examples, and tools:
-
Mathway provides a step-by-step breakdown of the process to simplify the square root of 160, from listing factors to finding the simplest radical form.
-
Khan Academy offers detailed video tutorials and practice exercises on simplifying square roots, including the use of rational exponents and radicals.
-
This resource explains the step-by-step process to simplify the square root of 160 using factorization and provides the solution in exact and decimal forms.
-
Symbolab's square root calculator can help verify your calculations and offers additional insights into the properties of square roots.
-
BYJU'S explores multiple methods for finding the square root of 160, including the prime factorization method, Newton’s method, and the long division method.
These resources provide various methods and tools for understanding and simplifying square roots, which can be particularly useful for students, educators, and anyone interested in mathematics.

FAQs on Simplifying Square Roots
Below are some frequently asked questions about simplifying square roots, along with detailed answers to help you understand the process better.
-
Q1: How do you simplify the square root of a non-perfect square number?
A: To simplify the square root of a non-perfect square number, follow these steps:
- Factor the number under the square root into its prime factors.
- Identify pairs of prime factors.
- Move each pair of prime factors outside the square root as a single number.
- Multiply the numbers outside the square root.
- Keep any remaining factors inside the square root.
For example, to simplify √160:
√160 = √(16 × 10) = √(42 × 10) = 4√10
-
Q2: Can you add or subtract square roots?
A: Yes, you can add or subtract square roots, but only if the values under the radical sign (the radicands) are the same. In that case, simply add or subtract the coefficients (the numbers in front of the radical). For example:
2√3 + 3√3 = (2 + 3)√3 = 5√3
-
Q3: How do you multiply square roots?
A: To multiply square roots, use the product rule of square roots, which states that √a × √b = √(a × b). For example:
√5 × √20 = √(5 × 20) = √100 = 10
-
Q4: How do you divide square roots?
A: To divide square roots, use the quotient rule of square roots, which states that √(a/b) = √a / √b. For example:
√50 / √2 = √(50 / 2) = √25 = 5
-
Q5: What are some common mistakes to avoid when simplifying square roots?
A: Common mistakes include:
- Not fully factoring the number under the square root.
- Incorrectly pairing factors.
- Forgetting to multiply the numbers outside the square root.
- Attempting to add or subtract square roots with different radicands.
For more detailed examples and explanations, consider exploring additional resources and study guides on simplifying square roots.
Đơn Giản Hóa Căn Bậc Hai (160) - Hướng Dẫn Chi Tiết
READ MORE:
Làm thế nào để đơn giản hóa √160?












