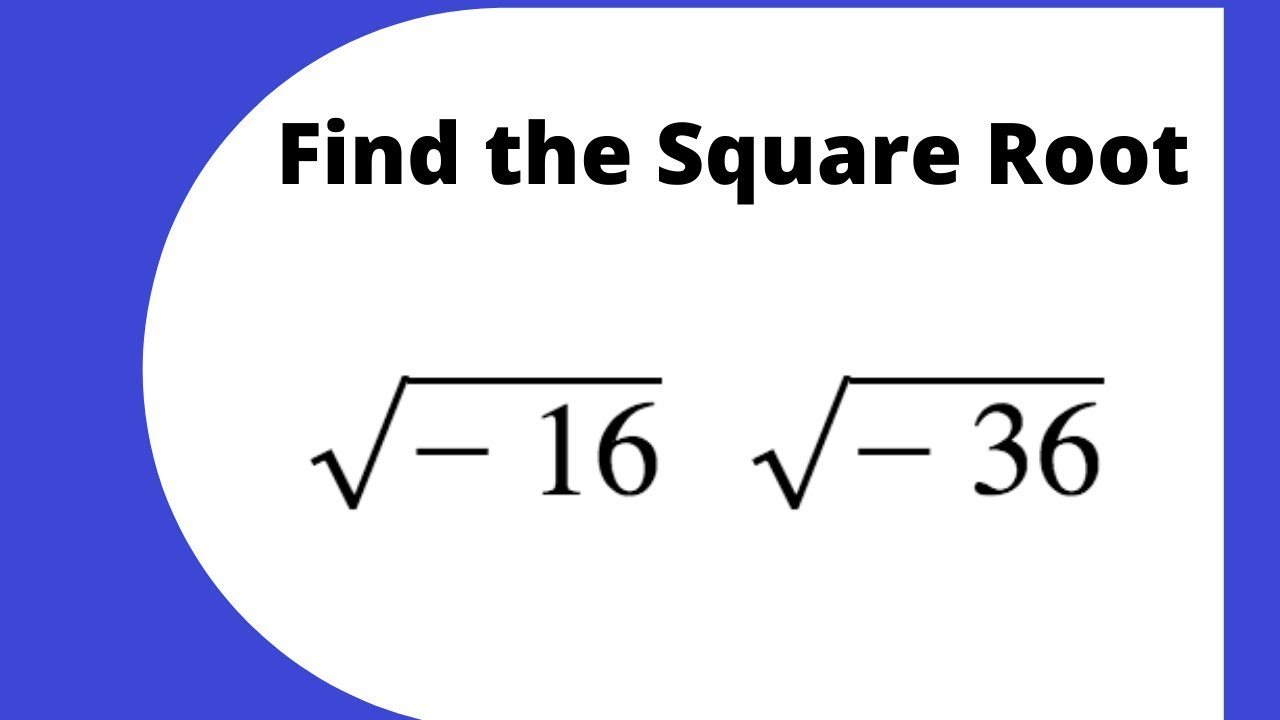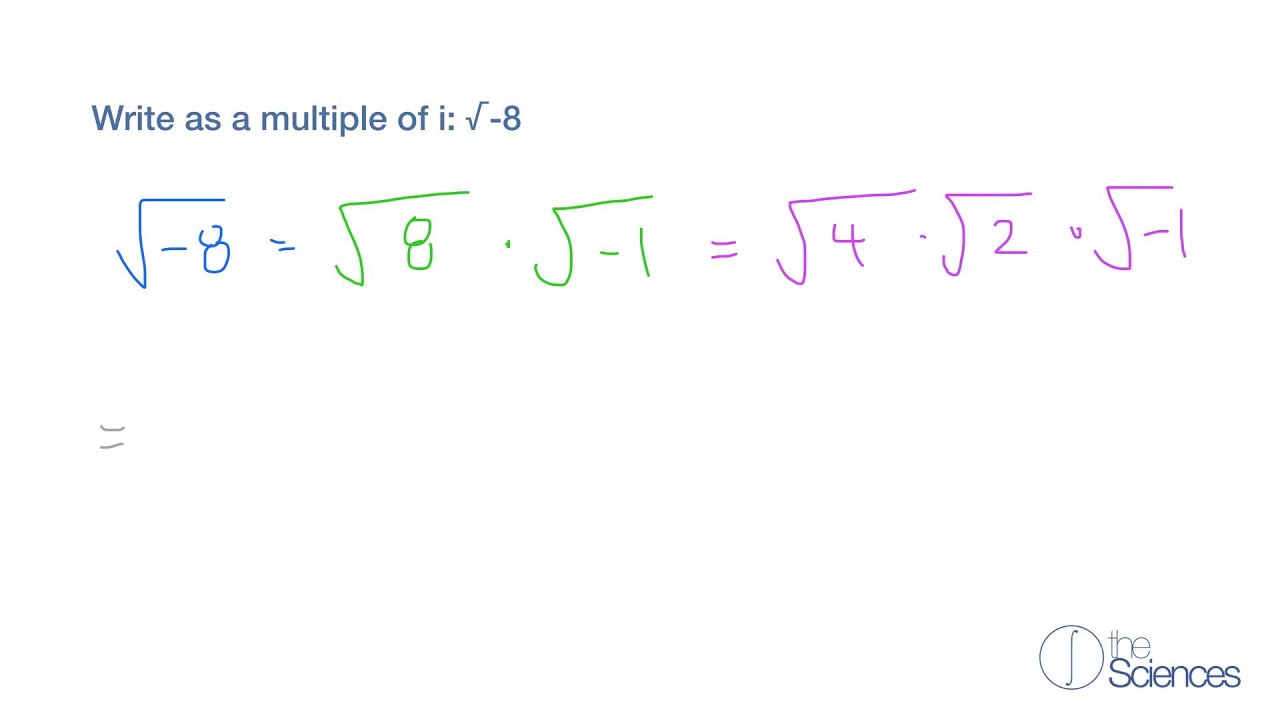Topic square root of 1 is: The square root of 1 is an essential mathematical concept with profound implications in both real and complex number systems. This article explores the definition, properties, and significance of the square root of 1, along with practical examples and applications to enhance your mathematical knowledge.
Table of Content
- Square Root of 1
- Introduction to Square Root
- Mathematical Definition of Square Root
- Properties of Square Roots
- Examples
- Square Root of 1
- Complex Numbers and the Square Root of 1
- Methods to Calculate the Square Root
- Examples Involving Square Root of 1
- Applications of the Square Root of 1
- Frequently Asked Questions (FAQs)
- Conclusion
- YOUTUBE: Khám phá ý nghĩa của căn bậc hai của -1 và những ứng dụng quan trọng trong toán học và khoa học. Video này sẽ giải thích chi tiết và rõ ràng.
Square Root of 1
The square root of a number is a value which, when multiplied by itself, gives the original number. The square root of 1 is a fundamental concept in mathematics and is often encountered in various mathematical problems and real-world applications.
Value of the Square Root of 1
The square root of 1 is:
\[\sqrt{1} = 1\]
This is because \(1 \times 1 = 1\). Hence, the square root of 1 is 1.
Properties of the Square Root of 1
- 1 is the only positive number whose square root is itself.
- 1 is a perfect square.
- In the context of complex numbers, the square root of 1 also includes -1, since \((-1) \times (-1) = 1\).
Mathematical Representation
The square root of 1 can be represented as:
\[\sqrt{1} = \pm1\]
However, in most cases, the positive root is considered, which is 1.
Applications of Square Root of 1
- Geometry: Used in various geometric calculations involving areas and perimeters.
- Algebra: Fundamental in solving quadratic equations.
- Physics: Appears in equations describing physical phenomena.
Examples
| Example | Calculation | Result |
|---|---|---|
| Square root of 1 | \(\sqrt{1}\) | 1 |
| Square of 1 | \(1^2\) | 1 |
FAQs on Square Root of 1
- What is the square root of 1?
- Can the square root of 1 be negative?
- Why is the square root of 1 important?
The square root of 1 is 1.
Yes, in the context of complex numbers, it can be -1.
It is a basic concept in mathematics that helps in understanding more complex mathematical principles.

READ MORE:
Introduction to Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square roots of 1 are 1 and -1 because both 1² and (-1)² equal 1. Square roots are fundamental in various fields of mathematics and are denoted by the radical symbol √.
Every nonnegative real number x has a unique nonnegative square root, called the principal square root, represented as √x. For example, the principal square root of 9 is 3, written as √9 = 3. Additionally, each positive number x has two square roots: √x (positive) and -√x (negative), collectively expressed as ±√x.
When discussing negative numbers, their square roots involve complex numbers, where i is the imaginary unit defined as √-1. Thus, the square root of -1 is i, and more generally, the square roots of any negative number are complex.
Mathematical Definition of Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical sign (√). For instance, the square root of 9 is 3, because \(3 \times 3 = 9\).
Mathematically, the square root operation is the inverse of squaring a number. If \(x^2 = a\), then \(x = \sqrt{a}\). This is expressed as:
- \(x^2 = a \implies x = \sqrt{a}\)
- \(4^2 = 16 \implies \sqrt{16} = 4\)
For any non-negative real number \(a\), the square root is always a non-negative number. This principal square root is denoted as \(\sqrt{a}\).
Properties of Square Roots
- Non-negativity: The square root of any non-negative number is non-negative.
- Principal Square Root: For any non-negative number \(a\), the principal square root is \(\sqrt{a}\).
- Two Roots: Every positive number \(a\) has two square roots: \(\sqrt{a}\) and \(-\sqrt{a}\).
- Square of Square Root: The square of the square root of a number \(a\) is \(a\) itself: \((\sqrt{a})^2 = a\).
Examples
| Number | Square Root |
| 1 | \(\pm 1\) |
| 4 | \(\pm 2\) |
| 9 | \(\pm 3\) |
For example, the square roots of 1 are 1 and -1, because both \(1 \times 1\) and \((-1) \times (-1)\) equal 1.
Understanding square roots is essential for solving quadratic equations, simplifying expressions, and performing various mathematical computations. Whether dealing with perfect squares or approximating the roots of non-perfect squares, the concept of square roots is fundamental in mathematics.

Square Root of 1
The square root of a number is a value that, when multiplied by itself, gives the original number. The square root of 1 is a unique case, as it has two roots: 1 and -1. This is because both \(1 \times 1\) and \(-1 \times -1\) equal 1.
In mathematical notation, the square root of 1 is represented as:
\[
\sqrt{1} = \pm 1
\]
Here, the symbol \(\pm\) indicates that there are both positive and negative roots.
Square roots play a crucial role in various areas of mathematics, including algebra, geometry, and calculus. Understanding the square root of 1 helps build a foundation for learning about complex numbers and other advanced mathematical concepts.
Additionally, the square root function is essential in solving quadratic equations, simplifying expressions, and analyzing graphs.
Overall, mastering the concept of square roots, starting with the basic example of the square root of 1, is fundamental for success in higher-level math.
Complex Numbers and the Square Root of 1
The square root of 1 in the context of complex numbers reveals interesting properties. Although the square root of 1 is straightforward in the realm of real numbers, resulting in ±1, its interpretation in the complex plane provides additional insights.
To understand the square root of 1 in the complex number system, we first need to revisit the definition of complex numbers. A complex number is typically written in the form \(a + bi\), where \(i\) is the imaginary unit, defined by the property \(i^2 = -1\).
- In the complex number system, every number can be represented in the form \(z = a + bi\), where \(a\) and \(b\) are real numbers, and \(i\) is the imaginary unit.
- The principal square root of 1 remains 1. However, the interpretation that also includes the negative root, -1, holds true since both \(1 \times 1 = 1\) and \((-1) \times (-1) = 1\).
For complex numbers, we explore solutions to the equation \(z^2 = 1\). These solutions are found by solving the polynomial equation:
- Rewrite the equation as \(z^2 - 1 = 0\).
- Factor the equation to \((z - 1)(z + 1) = 0\).
- Set each factor to zero: \(z - 1 = 0\) or \(z + 1 = 0\).
- This gives the solutions \(z = 1\) and \(z = -1\).
These steps confirm that the square roots of 1 in the complex plane are indeed ±1, the same as in the real number system.
Geometric Representation
On the complex plane, these roots can be visualized as points on the real axis at \(+1\) and \(-1\). The unit circle in the complex plane also intersects the real axis at these points, indicating that they are both one unit away from the origin (0,0).
Connection to Euler's Formula
Euler's formula, \(e^{i\theta} = \cos(\theta) + i\sin(\theta)\), provides a powerful way to express complex numbers. For the square root of 1, we can use Euler's formula to find:
\[ e^{i \cdot 0} = 1 \quad \text{and} \quad e^{i \cdot \pi} = -1 \]
These are the two roots \(1\) and \(-1\), respectively, when \(\theta = 0\) and \(\theta = \pi\), representing the full circle in the complex plane.
Applications in Complex Analysis
Understanding the square roots of numbers, including 1, is fundamental in complex analysis. It aids in solving equations involving complex numbers, analyzing electrical circuits, and in quantum mechanics.
Summary
Thus, while the square root of 1 may seem trivial in the real number domain, its complex number analysis reveals the depth and versatility of mathematical concepts. Both ±1 are equally important as roots of 1, showcasing the symmetry in the complex plane.
Methods to Calculate the Square Root
Calculating the square root of a number can be achieved through various methods, ranging from simple arithmetic techniques to more sophisticated algorithms. Here, we explore several methods to find the square root of a number, including both manual approaches and computational techniques.
1. Prime Factorization
This method involves breaking down the number into its prime factors and then grouping the factors into pairs.
- Find the prime factors of the number. For example, the prime factors of 36 are 2 × 2 × 3 × 3.
- Group the factors into pairs: (2 × 2) and (3 × 3).
- Take one factor from each pair and multiply them: 2 × 3 = 6.
- Thus, the square root of 36 is 6.
This method works best for perfect squares.
2. Long Division Method
The long division method is a manual algorithm to find the square root of a number to a certain number of decimal places.
- Pair the digits of the number from right to left. For example, for 529, we pair them as 5 and 29.
- Find the largest number whose square is less than or equal to the first pair. Here, it is 2 because \(2^2 = 4\).
- Subtract the square from the first pair and bring down the next pair of digits.
- Double the quotient (2 in this case) and place it as a divisor with a blank digit next to it.
- Find a digit (X) to fill in the blank that, when multiplied by the new divisor, gives a product less than or equal to the current dividend. Add X to the quotient.
- Repeat the process for additional pairs of digits to get more decimal places.
This method is useful for calculating the square root of non-perfect squares to high precision.
3. Newton's Method (Newton-Raphson Method)
This iterative method uses calculus to approximate the square root of a number.
- Start with an initial guess \( x_0 \). A reasonable starting point is often the number divided by 2.
- Apply the iterative formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{a}{x_n} \right) \), where \( a \) is the number whose square root is being calculated.
- Continue the iterations until the difference between successive values is within a desired tolerance.
For example, to find the square root of 10 with an initial guess of 3:
\[
x_1 = \frac{1}{2} \left( 3 + \frac{10}{3} \right) = 3.1667
\]
\[
x_2 = \frac{1}{2} \left( 3.1667 + \frac{10}{3.1667} \right) \approx 3.1623
\]
This method converges quickly to the actual square root.
4. Using a Calculator
Most modern calculators have a built-in square root function, usually denoted by the symbol √. Simply enter the number and press the √ button to find the square root. This is the quickest and easiest method for most practical purposes.
5. Estimation and Refinement
For an approximation, you can use the method of guessing and refining:
- Make an initial guess. For example, guess that the square root of 50 is around 7, since \(7^2 = 49\).
- Refine the guess by averaging the guess with the quotient of the number divided by the guess: \(\frac{\text{guess} + \frac{\text{number}}{\text{guess}}}{2}\).
- Repeat the process to get closer approximations.
Comparison of Methods
| Method | Best Use Case | Accuracy |
|---|---|---|
| Prime Factorization | Perfect squares | Exact for perfect squares |
| Long Division | Manual calculation to many decimal places | High accuracy with more iterations |
| Newton's Method | Calculus-based and iterative refinement | Very high accuracy |
| Calculator | Quick and practical for everyday use | Depends on the calculator's precision |
| Estimation and Refinement | Quick approximation | Improves with each refinement |
Each method has its advantages depending on the context and the required precision. Understanding these methods provides a deeper insight into the mathematics behind square roots.
Examples Involving Square Root of 1
The square root of 1 is a fundamental concept in mathematics with applications across various domains. Here, we explore a range of examples demonstrating how the square root of 1 is used in different mathematical contexts.
1. Basic Algebra
In algebra, solving the equation \( x^2 = 1 \) involves finding the square roots of 1.
- Example: Solve \( x^2 = 1 \).
- Solution: The solutions are \( x = 1 \) and \( x = -1 \), since both \( 1^2 = 1 \) and \( (-1)^2 = 1 \).
2. Quadratic Equations
The square root of 1 often appears in the solutions of quadratic equations. For instance, consider the quadratic equation \( x^2 - 2x + 1 = 0 \).
- Rewrite the equation as \( (x - 1)^2 = 0 \).
- Taking the square root of both sides gives \( x - 1 = 0 \).
- Thus, \( x = 1 \) is the solution.
3. Complex Numbers
In the context of complex numbers, the square root of 1 includes both 1 and -1. This is particularly useful in solving equations involving complex roots.
- Example: Solve \( z^2 = 1 \) in the complex plane.
- Solution: The solutions are \( z = 1 \) and \( z = -1 \), as these are the points where the function intersects the real axis.
4. Trigonometry and Unit Circle
On the unit circle, the points corresponding to the square root of 1 are where the circle intersects the real axis.
- Example: Identify the points on the unit circle where the square root of 1 is located.
- Solution: These points are (1, 0) and (-1, 0), representing the angles 0 and \( \pi \) radians.
5. Matrices and Linear Algebra
In linear algebra, the square root of 1 can be found in the eigenvalues of matrices. For example, consider a matrix with eigenvalues that are square roots of 1.
- Example: Find the eigenvalues of the matrix \( A = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \).
- Solution: The eigenvalues are the diagonal elements, 1 and -1, which are the square roots of 1.
6. Geometry
In geometry, the distance calculations often involve the square root of 1. For instance, calculating the distance between points on a grid.
- Example: Calculate the distance between the points (1,0) and (2,0) on a coordinate plane.
- Solution: The distance \( d \) is given by \( d = \sqrt{(2-1)^2} = \sqrt{1} = 1 \).
7. Logarithms
Logarithmic functions involving the square root of 1 often simplify the calculations. For example, using the properties of logarithms:
- Example: Simplify \( \log(\sqrt{1}) \).
- Solution: Since \( \sqrt{1} = 1 \), and \( \log(1) = 0 \), it follows that \( \log(\sqrt{1}) = 0 \).
Summary
These examples illustrate the versatile applications of the square root of 1 across different areas of mathematics. Whether in solving equations, analyzing geometric distances, or working with complex numbers, the square root of 1 plays a crucial role.

Applications of the Square Root of 1
The square root of 1, which results in both 1 and -1, has significant applications across various fields of mathematics and beyond. Below, we explore some key areas where the concept of the square root of 1 is applied.
1. Algebra and Equation Solving
In algebra, understanding the square root of 1 is crucial for solving polynomial equations. For instance, in the equation \(x^2 = 1\), the solutions are \(x = 1\) and \(x = -1\). This forms the basis for solving more complex algebraic problems where recognizing the possible roots of an equation is essential.
- Example: Solve \(x^4 - x^2 = 0\).
- Solution: Factor the equation as \(x^2(x^2 - 1) = 0\), leading to \(x^2 = 0\) or \(x^2 = 1\). Thus, the roots are \(x = 0, x = 1, x = -1\).
2. Complex Numbers and Euler's Formula
The square root of 1 is integral in the realm of complex numbers and their applications. Using Euler's formula \(e^{i\theta} = \cos(\theta) + i\sin(\theta)\), we find that for \( \theta = 0 \) and \( \theta = \pi \), the values are \( e^{i \cdot 0} = 1 \) and \( e^{i \cdot \pi} = -1 \), demonstrating the fundamental relationship of 1 and -1 on the unit circle.
In practical applications, these concepts are used in fields such as signal processing and electrical engineering.
3. Matrices and Eigenvalues
In linear algebra, the square root of 1 appears frequently in the context of matrices. For example, the eigenvalues of certain matrices can be 1 or -1, which are the square roots of 1. These eigenvalues are pivotal in various transformations and stability analysis in systems theory.
- Example: Consider the identity matrix \( I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \).
- The eigenvalues of \( I \) are 1, which are the square roots of 1, indicating that the matrix scales vectors without changing their direction.
4. Trigonometry and the Unit Circle
In trigonometry, the square root of 1 plays a role in understanding angles and coordinates on the unit circle. The points where the unit circle intersects the real axis at 1 and -1 correspond to the angles of 0 and \( \pi \) radians, respectively.
- Example: Evaluate \( \cos(\pi) \) and \( \cos(0) \).
- Solution: Both angles are points where the square root of 1 is applicable, resulting in \( \cos(0) = 1 \) and \( \cos(\pi) = -1 \).
5. Financial Models
In finance, the square root of 1 is used in various calculations, including in the evaluation of rates of return and in certain risk models. Understanding how positive and negative factors impact financial models is analogous to considering the roots ±1.
6. Engineering and Control Systems
In control systems and signal processing, the concept of the square root of 1 is used in analyzing stability and feedback loops. Systems often need to handle oscillations and signals that can be represented with positive and negative unity values.
- Example: A control system may need to evaluate how a unit feedback loop responds to different input signals.
- Application: Determining the system's behavior involves understanding how it responds to inputs that are scaled by ±1.
7. Quantum Mechanics
In quantum mechanics, the square root of 1 is relevant in understanding the superposition and phase factors of wave functions. These wave functions can be manipulated using unitary operations, where understanding the roots of 1 helps in analyzing phase shifts.
Summary
The applications of the square root of 1 are vast and varied, spanning from fundamental algebra to advanced engineering and quantum physics. Recognizing the dual nature of the square root of 1 (both 1 and -1) provides deeper insights and solutions across many scientific and mathematical fields.
Frequently Asked Questions (FAQs)
Here are some common questions and detailed answers regarding the square root of 1:
-
What is the square root of 1?
The square root of 1 is 1. Mathematically, this can be expressed as:
\[\sqrt{1} = 1\]
-
Why is the square root of 1 equal to 1?
The square root of a number is a value that, when multiplied by itself, gives the original number. Since:
\[1 \times 1 = 1\]
The square root of 1 is 1.
-
Are there any other square roots of 1?
Yes, there is also a negative square root. The other square root of 1 is -1, because:
\[-1 \times -1 = 1\]
Therefore, we have:
\[\sqrt{1} = \pm 1\]
-
Is the square root of 1 considered a real number?
Yes, both 1 and -1 are real numbers.
-
Does the square root of 1 have any special properties?
Yes, the square root of 1 is unique in that it is the only positive integer that has itself and its negative as square roots.
-
How is the square root of 1 used in complex numbers?
In the context of complex numbers, the square root of 1 is often referenced because it has implications for both the real and imaginary unit (i.e., i). However, since 1 is a real number, its square roots are not complex.
Conclusion
The square root of 1 holds a unique position in mathematics due to its simplicity and the fundamental concepts it represents. The square root of 1 is both 1 and -1 because both numbers, when squared, return 1. This property highlights the dual nature of square roots, which can have both positive and negative values.
Understanding the square root of 1 is essential not just for basic arithmetic but also for more advanced mathematical concepts, including algebra and complex numbers. The ability to recognize and apply the properties of the square root of 1 aids in simplifying expressions and solving equations efficiently.
Here are some key takeaways:
- The square root of 1 (\(\sqrt{1}\)) is both 1 and -1.
- This concept is crucial in both real and complex number systems.
- It provides a foundation for understanding more complex mathematical ideas.
Moreover, the square root of 1 is frequently encountered in various mathematical problems and proofs. Its significance extends beyond pure mathematics to fields such as physics and engineering, where it helps in solving equations that describe natural phenomena.
In summary, mastering the concept of the square root of 1 and its properties is an essential step in the journey through mathematics. It not only helps in solving problems more effectively but also enhances the overall understanding of mathematical principles.
Khám phá ý nghĩa của căn bậc hai của -1 và những ứng dụng quan trọng trong toán học và khoa học. Video này sẽ giải thích chi tiết và rõ ràng.
Căn bậc hai của -1 là gì?
READ MORE:
Tìm hiểu căn bậc hai của 1, những tính chất đặc biệt và cách tính toán dễ hiểu qua video này. Video cung cấp thông tin chi tiết và hữu ích.
CĂN BẬC HAI CỦA 1