Topic square root of 1-30: Discover the fascinating world of square roots with our comprehensive guide on the square root of 1-30. Learn the mathematical definitions, calculation methods, and practical applications of square roots. This article provides a detailed chart and table, along with visual representations to help you understand and master the concept of square roots effectively.
Table of Content
- Square Roots of Numbers from 1 to 30
- Introduction to Square Roots
- Understanding Square Roots
- Mathematical Definition of Square Roots
- Symbol and Notation of Square Roots
- Square Roots from 1 to 30: Chart and Table
- Calculation Methods for Square Roots
- Prime Factorization Method
- Long Division Method
- Perfect Squares and Their Roots
- Applications of Square Roots in Real Life
- Visual Representation of Square Roots
- Common Mistakes and How to Avoid Them
- Square Root Calculation Tools and Resources
- Frequently Asked Questions
- Conclusion and Further Reading
- YOUTUBE: Video hướng dẫn về căn bậc hai từ 1 đến 30 và cách viết các số chính phương từ 1 đến 30. Phù hợp với những ai muốn tìm hiểu về toán học cơ bản và các khái niệm liên quan đến căn bậc hai.
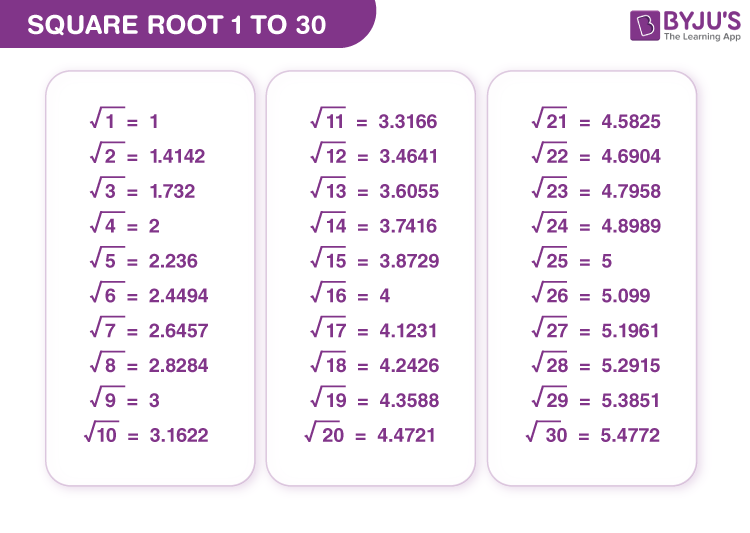
Square Roots of Numbers from 1 to 30
The square root of a number is a value that, when multiplied by itself, gives the original number. Here, we explore the square roots of numbers from 1 to 30, which can be useful for various mathematical calculations and learning purposes.
Table of Square Roots from 1 to 30
| Number | Square Root |
|---|---|
| 1 | \(\sqrt{1} = 1\) |
| 2 | \(\sqrt{2} \approx 1.414\) |
| 3 | \(\sqrt{3} \approx 1.732\) |
| 4 | \(\sqrt{4} = 2\) |
| 5 | \(\sqrt{5} \approx 2.236\) |
| 6 | \(\sqrt{6} \approx 2.449\) |
| 7 | \(\sqrt{7} \approx 2.646\) |
| 8 | \(\sqrt{8} \approx 2.828\) |
| 9 | \(\sqrt{9} = 3\) |
| 10 | \(\sqrt{10} \approx 3.162\) |
| 11 | \(\sqrt{11} \approx 3.317\) |
| 12 | \(\sqrt{12} \approx 3.464\) |
| 13 | \(\sqrt{13} \approx 3.606\) |
| 14 | \(\sqrt{14} \approx 3.742\) |
| 15 | \(\sqrt{15} \approx 3.873\) |
| 16 | \(\sqrt{16} = 4\) |
| 17 | \(\sqrt{17} \approx 4.123\) |
| 18 | \(\sqrt{18} \approx 4.243\) |
| 19 | \(\sqrt{19} \approx 4.359\) |
| 20 | \(\sqrt{20} \approx 4.472\) |
| 21 | \(\sqrt{21} \approx 4.583\) |
| 22 | \(\sqrt{22} \approx 4.690\) |
| 23 | \(\sqrt{23} \approx 4.796\) |
| 24 | \(\sqrt{24} \approx 4.899\) |
| 25 | \(\sqrt{25} = 5\) |
| 26 | \(\sqrt{26} \approx 5.099\) |
| 27 | \(\sqrt{27} \approx 5.196\) |
| 28 | \(\sqrt{28} \approx 5.292\) |
| 29 | \(\sqrt{29} \approx 5.385\) |
| 30 | \(\sqrt{30} \approx 5.477\) |
Summary
The table above provides the square roots of numbers from 1 to 30. These values are useful for solving mathematical problems and understanding the properties of numbers. By learning these values, one can enhance their mathematical computation skills and accuracy.

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics and is widely used in various fields, from engineering to everyday problem-solving. A square root of a number x is a number y such that \( y^2 = x \). In other words, the square root of a number is one of its two equal factors. The square root symbol is √, and the square root of x is represented as \( \sqrt{x} \).
For example, the square root of 25 is 5 because \( 5^2 = 25 \). Similarly, the square root of 9 is 3 because \( 3^2 = 9 \). Square roots can be either positive or negative, but in most contexts, the principal (positive) square root is considered.
To better understand square roots, it's useful to start with perfect squares. Perfect squares are numbers that have integer square roots. Here is a list of some perfect squares and their corresponding square roots:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
For non-perfect squares, square roots are often irrational numbers, meaning they cannot be expressed as a simple fraction. For instance, \( \sqrt{2} \approx 1.414 \) and \( \sqrt{3} \approx 1.732 \). These values are usually approximated for practical purposes.
Understanding square roots is crucial for solving quadratic equations, understanding geometric properties, and analyzing various scientific phenomena. In subsequent sections, we will explore different methods to calculate square roots, their applications, and common mistakes to avoid.
Understanding Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 25 is 5 because \( 5 \times 5 = 25 \). Mathematically, the square root of a number \( x \) is denoted as \( \sqrt{x} \) and in exponential form as \( x^{1/2} \).
Square roots can be classified into two main categories: perfect squares and non-perfect squares. Perfect squares are numbers like 1, 4, 9, 16, and 25, which have whole numbers as their square roots. For example:
- \( \sqrt{1} = 1 \)
- \( \sqrt{4} = 2 \)
- \( \sqrt{9} = 3 \)
- \( \sqrt{16} = 4 \)
- \( \sqrt{25} = 5 \)
Non-perfect squares do not have whole number square roots and are usually irrational numbers. These cannot be expressed as simple fractions and their decimal form is non-terminating and non-repeating. Some examples include:
- \( \sqrt{2} \approx 1.414 \)
- \( \sqrt{3} \approx 1.732 \)
- \( \sqrt{5} \approx 2.236 \)
- \( \sqrt{6} \approx 2.449 \)
- \( \sqrt{7} \approx 2.646 \)
The table below lists the square roots of numbers from 1 to 30:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3 |
| 10 | 3.162 |
| 11 | 3.317 |
| 12 | 3.464 |
| 13 | 3.606 |
| 14 | 3.742 |
| 15 | 3.873 |
| 16 | 4 |
| 17 | 4.123 |
| 18 | 4.243 |
| 19 | 4.359 |
| 20 | 4.472 |
| 21 | 4.583 |
| 22 | 4.690 |
| 23 | 4.796 |
| 24 | 4.899 |
| 25 | 5 |
| 26 | 5.099 |
| 27 | 5.196 |
| 28 | 5.292 |
| 29 | 5.385 |
| 30 | 5.477 |
Understanding the concept of square roots is essential for many areas of mathematics, including algebra, geometry, and calculus. It is also useful in real-world applications such as calculating areas, solving equations, and analyzing scientific data.
Mathematical Definition of Square Roots
A square root of a number is a value that, when multiplied by itself, gives the original number. The square root of a number \( x \) is denoted as \( \sqrt{x} \). In mathematical notation, if \( y \) is the square root of \( x \), then \( y \times y = x \) or \( y^2 = x \).
Square roots can be represented in two main forms:
- Radical Form: This is the most common way to represent square roots using the radical symbol (√). For example, the square root of 16 is written as \( \sqrt{16} \).
- Exponential Form: This form uses fractional exponents to represent square roots. For instance, the square root of 16 can also be written as \( 16^{1/2} \).
Square roots are classified into two types:
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are integers. For example, \( \sqrt{25} = 5 \) because \( 5^2 = 25 \).
- Non-Perfect Squares: Numbers such as 2, 3, 5, and 7 are non-perfect squares because their square roots are not whole numbers and are irrational. For example, \( \sqrt{2} \approx 1.414 \), which cannot be expressed as a simple fraction.
The following table lists the square roots of numbers from 1 to 30:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3 |
| 10 | 3.162 |
| 11 | 3.317 |
| 12 | 3.464 |
| 13 | 3.606 |
| 14 | 3.742 |
| 15 | 3.873 |
| 16 | 4 |
| 17 | 4.123 |
| 18 | 4.243 |
| 19 | 4.359 |
| 20 | 4.472 |
| 21 | 4.583 |
| 22 | 4.690 |
| 23 | 4.796 |
| 24 | 4.899 |
| 25 | 5 |
| 26 | 5.099 |
| 27 | 5.196 |
| 28 | 5.292 |
| 29 | 5.385 |
| 30 | 5.477 |
Understanding the mathematical definition of square roots is crucial for solving various algebraic equations and geometric problems. Square roots also play a significant role in higher-level mathematics, including calculus and complex number theory.
Symbol and Notation of Square Roots
The square root of a number is a value that, when multiplied by itself, results in the original number. The symbol used to denote a square root is called the radical symbol, represented as "√". The number under the radical symbol is known as the radicand.
Here are the key notations and examples for square roots:
- Radical Form: This is the standard notation where the square root of a number \( x \) is written as \( \sqrt{x} \). For example, the square root of 16 is written as \( \sqrt{16} \).
- Exponential Form: Square roots can also be expressed using fractional exponents. The square root of \( x \) can be written as \( x^{1/2} \). For instance, \( \sqrt{16} \) can be written as \( 16^{1/2} \).
In mathematical notation, the square root function has some fundamental properties and rules:
| Property | Example |
|---|---|
| \( \sqrt{x^2} = x \) | \( \sqrt{5^2} = 5 \) |
| \( (\sqrt{x})^2 = x \) | \( (\sqrt{7})^2 = 7 \) |
| \( \sqrt{x \cdot y} = \sqrt{x} \cdot \sqrt{y} \) | \( \sqrt{3 \cdot 12} = \sqrt{36} = 6 \) |
| \( \frac{\sqrt{x}}{\sqrt{y}} = \sqrt{\frac{x}{y}} \) | \( \frac{\sqrt{24}}{\sqrt{6}} = \sqrt{4} = 2 \) |
For practical purposes, it is important to recognize the values of square roots for common numbers. Below is a table of square roots for numbers from 1 to 30:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3 |
| 10 | 3.162 |
| 11 | 3.317 |
| 12 | 3.464 |
| 13 | 3.606 |
| 14 | 3.742 |
| 15 | 3.873 |
| 16 | 4 |
| 17 | 4.123 |
| 18 | 4.243 |
| 19 | 4.359 |
| 20 | 4.472 |
| 21 | 4.583 |
| 22 | 4.690 |
| 23 | 4.796 |
| 24 | 4.899 |
| 25 | 5 |
| 26 | 5.099 |
| 27 | 5.196 |
| 28 | 5.292 |
| 29 | 5.385 |
| 30 | 5.477 |
Understanding the symbols and notation of square roots is essential for solving various mathematical problems, including those in algebra, geometry, and higher mathematics. Mastery of these concepts enhances computational accuracy and problem-solving skills.

Square Roots from 1 to 30: Chart and Table
Understanding the square roots of numbers from 1 to 30 is essential for many mathematical applications, including algebra and geometry. Here, we provide a detailed chart and table for quick reference.
The square root of a number is a value that, when multiplied by itself, gives the original number. This is represented using the radical symbol (√). For example, the square root of 9 is 3 because \( 3 \times 3 = 9 \).
Below is a comprehensive table listing the square roots of numbers from 1 to 30:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3 |
| 10 | 3.162 |
| 11 | 3.317 |
| 12 | 3.464 |
| 13 | 3.606 |
| 14 | 3.742 |
| 15 | 3.873 |
| 16 | 4 |
| 17 | 4.123 |
| 18 | 4.243 |
| 19 | 4.359 |
| 20 | 4.472 |
| 21 | 4.583 |
| 22 | 4.690 |
| 23 | 4.796 |
| 24 | 4.899 |
| 25 | 5 |
| 26 | 5.099 |
| 27 | 5.196 |
| 28 | 5.292 |
| 29 | 5.385 |
| 30 | 5.477 |
This table helps in quickly identifying the square roots of the numbers from 1 to 30. It's important to note that some numbers have integer square roots (perfect squares), while others have irrational square roots (non-perfect squares), which cannot be expressed as simple fractions and have non-terminating, non-repeating decimal forms.
Here's a chart representation for visual learners:
Mastering these values is crucial for enhancing computational accuracy and speed, especially when solving equations and working on geometric problems.
Calculation Methods for Square Roots
Calculating the square root of a number can be approached using various methods, each suitable for different types of numbers and levels of precision required. Below are some commonly used methods to find the square root of numbers from 1 to 30:
1. Prime Factorization Method
This method involves expressing the number as a product of its prime factors. By pairing the prime factors, the square root can be found by taking one factor from each pair.
- Find the prime factors of the number.
- Group the prime factors into pairs.
- Take one number from each pair and multiply them together.
Example: To find the square root of 36:
- Prime factors of 36: \(36 = 2 \times 2 \times 3 \times 3\)
- Pair the factors: \((2 \times 2) \times (3 \times 3)\)
- Take one factor from each pair: \(2 \times 3 = 6\)
2. Long Division Method
The long division method is a manual algorithm that provides a systematic approach to finding the square root of a number. This method is particularly useful for larger numbers and can give a high degree of precision.
- Write the number in pairs of digits starting from the decimal point.
- Find the largest number whose square is less than or equal to the first pair.
- Subtract this square from the first pair and bring down the next pair.
- Double the current quotient and find a new digit that fits.
- Repeat the process until the desired precision is achieved.
Example: To find the square root of 15 using the long division method:
- Write 15 as 15.000000.
- Find the largest number whose square is less than 15 (3, since \(3^2 = 9\)).
- Subtract: \(15 - 9 = 6\). Bring down the next pair (60).
- Double the quotient (3) to get 6. Find a new digit (2) so \(62 \times 2 \leq 600\).
- Repeat to get the square root as approximately 3.872.
3. Estimation Method
This method is useful for quickly approximating the square root of a number by identifying the nearest perfect squares.
- Identify the two closest perfect squares between which the number lies.
- Estimate the square root by averaging or interpolation.
Example: To estimate the square root of 20:
- Identify the nearest perfect squares (16 and 25).
- Since \(16 < 20 < 25\), and \( \sqrt{16} = 4\) and \( \sqrt{25} = 5\), the square root of 20 is approximately between 4 and 5.
- Estimate: \(4.5\) (closer approximation can be refined further).
4. Using a Calculator
The most straightforward method is to use a scientific calculator, which has a dedicated function to compute the square root directly.
- Enter the number into the calculator.
- Press the square root (√) button.
- Read the result displayed.
These methods provide various approaches to calculating square roots, each with its advantages depending on the context and the level of accuracy required.
Prime Factorization Method
The prime factorization method is a systematic approach to find the square root of a number by expressing it as a product of prime factors. This method is particularly useful for perfect squares. Below are the detailed steps to find the square root using the prime factorization method:
- Identify the Prime Factors: Break down the number into its prime factors by dividing it by the smallest prime numbers until you reach 1.
- Group the Prime Factors: Pair the prime factors. Each pair represents a factor that can be taken out of the square root.
- Calculate the Square Root: Multiply one number from each pair of prime factors to get the square root of the original number.
Let's illustrate this method with a few examples:
Example 1: Finding the Square Root of 36
- Step 1: Identify the prime factors of 36.
- 36 = 2 × 2 × 3 × 3
- Step 2: Group the prime factors into pairs.
- (2 × 2) and (3 × 3)
- Step 3: Take one number from each pair and multiply them.
- 2 × 3 = 6
Therefore, \( \sqrt{36} = 6 \).
Example 2: Finding the Square Root of 225
- Step 1: Identify the prime factors of 225.
- 225 = 3 × 3 × 5 × 5
- Step 2: Group the prime factors into pairs.
- (3 × 3) and (5 × 5)
- Step 3: Take one number from each pair and multiply them.
- 3 × 5 = 15
Therefore, \( \sqrt{225} = 15 \).
Example 3: Finding the Square Root of 30
- Step 1: Identify the prime factors of 30.
- 30 = 2 × 3 × 5
- Step 2: Since 30 is not a perfect square, the factors cannot be paired equally.
- Step 3: The square root of 30 is expressed in its simplest radical form.
- √30 = √(2 × 3 × 5) = √2 × √3 × √5 ≈ 1.414 × 1.732 × 2.236 ≈ 5.477
Therefore, \( \sqrt{30} \approx 5.477 \).
The prime factorization method is efficient for perfect squares but can also be used to simplify square roots of non-perfect squares by expressing them in their simplest radical form.
Long Division Method
The long division method is a systematic way to find the square root of a number, especially useful for both perfect and non-perfect squares. This method involves a step-by-step process that provides an accurate result by handling one digit at a time. Below are the detailed steps to find the square root using the long division method:
- Write the Number in Decimal Form: If the number is not already in decimal form, add trailing zeros to ensure precision. For example, to find the square root of 30, write it as 30.000000.
- Pair the Digits: Starting from the decimal point, pair the digits by placing a bar over each pair. For 30, it would be 30.00 00 00.
- Initial Division: Find the largest number whose square is less than or equal to the first pair. For 30, the first pair is 30. The largest number whose square (5 × 5 = 25) is less than 30 is 5.
- Calculate the Remainder: Subtract this square from the first pair to get the remainder. Here, 30 - 25 = 5. Bring down the next pair of zeros to get 500.
- Form the New Divisor: Double the current quotient (5 × 2 = 10) and write it down with a blank on its right: 10_. Find a digit to fill the blank such that when this new number is multiplied by the same digit, the product is less than or equal to 500. For instance, 104 × 4 = 416.
- Repeat the Process: Subtract the product from the current dividend to get a new remainder (500 - 416 = 84). Bring down the next pair of zeros to make it 8400.
- Continue Until Desired Precision: Continue this process until you have achieved the desired level of accuracy. Each step involves doubling the current quotient, finding the appropriate digit, and forming a new divisor.
Let’s go through an example to illustrate this method:
Example: Finding the Square Root of 30
- Step 1: Write 30 as 30.000000.
- Step 2: Pair the digits: 30.00 00 00.
- Step 3: The largest number whose square is ≤ 30 is 5 (since \(5^2 = 25\)).
- Step 4: Subtract to get the remainder: 30 - 25 = 5. Bring down the next pair to get 500.
- Step 5: Double the quotient: 5 × 2 = 10, forming 10_. The largest digit that fits is 4 (since \(104 \times 4 = 416\)).
- Step 6: Subtract to get the new remainder: 500 - 416 = 84. Bring down the next pair to get 8400.
- Step 7: Double the quotient: 54 × 2 = 108, forming 108_. The largest digit that fits is 7 (since \(1087 \times 7 = 7609\)).
- Step 8: Subtract to get the new remainder: 8400 - 7609 = 791. Continue the process for more precision.
The square root of 30 using the long division method is approximately 5.477.
This method, while time-consuming, is highly effective for accurately calculating square roots by breaking down the problem into manageable steps.

Perfect Squares and Their Roots
Perfect squares are integers that are the square of an integer. In other words, a number is a perfect square if it can be expressed as the product of an integer with itself. Below is a list of perfect squares from 1 to 30, along with their corresponding square roots.
| Number | Perfect Square | Square Root |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 4 | 2 |
| 3 | 9 | 3 |
| 4 | 16 | 4 |
| 5 | 25 | 5 |
These are the perfect squares for numbers from 1 to 5. We can extend this list to include all numbers up to 30:
- 6: Perfect square is 36, and the square root is 6.
- 7: Perfect square is 49, and the square root is 7.
- 8: Perfect square is 64, and the square root is 8.
- 9: Perfect square is 81, and the square root is 9.
- 10: Perfect square is 100, and the square root is 10.
- 11: Perfect square is 121, and the square root is 11.
- 12: Perfect square is 144, and the square root is 12.
- 13: Perfect square is 169, and the square root is 13.
- 14: Perfect square is 196, and the square root is 14.
- 15: Perfect square is 225, and the square root is 15.
- 16: Perfect square is 256, and the square root is 16.
- 17: Perfect square is 289, and the square root is 17.
- 18: Perfect square is 324, and the square root is 18.
- 19: Perfect square is 361, and the square root is 19.
- 20: Perfect square is 400, and the square root is 20.
- 21: Perfect square is 441, and the square root is 21.
- 22: Perfect square is 484, and the square root is 22.
- 23: Perfect square is 529, and the square root is 23.
- 24: Perfect square is 576, and the square root is 24.
- 25: Perfect square is 625, and the square root is 25.
- 26: Perfect square is 676, and the square root is 26.
- 27: Perfect square is 729, and the square root is 27.
- 28: Perfect square is 784, and the square root is 28.
- 29: Perfect square is 841, and the square root is 29.
- 30: Perfect square is 900, and the square root is 30.
By understanding these perfect squares and their roots, you can easily identify the square roots of numbers from 1 to 30. Knowing perfect squares also helps in various mathematical calculations and problem-solving scenarios.
Applications of Square Roots in Real Life
Square roots are more than just abstract mathematical concepts; they have a multitude of practical applications in various fields. Here are some significant ways in which square roots are utilized in real life:
- Geometry and Architecture: Square roots are fundamental in calculating areas and dimensions, which is essential for designing buildings and structures. For example, if the area of a square plot is known, its side length can be determined by taking the square root of the area.
- Finance: In finance, square roots are used in the computation of compound interest rates and risk assessment models. They help in determining the standard deviation, which measures the volatility or risk associated with a financial asset.
- Physics and Engineering: Square roots appear in various formulas related to motion, energy, and resistance. For instance, in physics, the speed of an object falling freely under gravity is proportional to the square root of the distance it falls.
- Statistics and Probability: Square roots are involved in calculating standard deviations, a key concept in statistics for understanding data variability. This helps in making sense of data distribution and spread.
- Computer Science: Algorithms that involve geometric and graphic computations often use square roots to optimize calculations. For example, the distance formula in 2D and 3D graphics uses square roots to determine the distance between points.
- Education: Learning about square roots enhances problem-solving skills and promotes logical thinking. It is a fundamental concept that lays the groundwork for more advanced mathematical studies.
These applications highlight the importance of understanding square roots, demonstrating their utility in both everyday life and various professional fields.
Visual Representation of Square Roots
Visualizing square roots helps in understanding their properties and how they relate to geometric concepts. Here are some common methods for visual representation of square roots:
Geometric Interpretation
One of the most intuitive ways to represent square roots is through geometry. A square root can be seen as the side length of a square with a given area.
- Perfect Squares: For perfect squares, the square root is an integer. For example, a square with an area of 9 square units has a side length of 3 units because \( \sqrt{9} = 3 \).
- Non-Perfect Squares: For non-perfect squares, the square root is not an integer and can be represented by approximating the side length. For instance, the square root of 2 can be represented as the side length of a square with an area of 2 square units.
Number Line Representation
Square roots can also be represented on a number line. This helps in visualizing the relative size of square roots between integers.
- Mark the integers on the number line.
- Approximate the square roots by identifying their positions between the integers. For example, \( \sqrt{2} \) is approximately 1.414, which lies between 1 and 2 on the number line.
Graphical Representation
Using graphs to plot square root functions provides a clear visual understanding of how square roots behave.
- Square Root Function: The graph of \( y = \sqrt{x} \) shows the relationship between x and its square root. The curve starts at (0,0) and increases gradually, illustrating that as x increases, \( \sqrt{x} \) also increases.
- Comparing Values: Graphing both x and \( \sqrt{x} \) on the same axes helps in comparing the values. The function \( y = \sqrt{x} \) will always be below the line \( y = x \), showing that square roots are always less than the original number (except for 1).
Visual Aids and Charts
Using visual aids like square root charts can enhance understanding. These charts typically display the square roots of numbers from 1 to 30, showing both the square root and the original number. Here is a basic example:
| Number | Square Root |
|---|---|
| 1 | \(\sqrt{1} = 1\) |
| 2 | \(\sqrt{2} \approx 1.414\) |
| 3 | \(\sqrt{3} \approx 1.732\) |
| 4 | \(\sqrt{4} = 2\) |
| 5 | \(\sqrt{5} \approx 2.236\) |
| ... | ... |
| 30 | \(\sqrt{30} \approx 5.477\) |
Interactive Tools
There are many online tools and software that allow for interactive visualizations of square roots. These tools can help in dynamically illustrating how the square root values change with different inputs, aiding in a deeper understanding of the concept.
Common Mistakes and How to Avoid Them
Understanding common mistakes made while calculating square roots and knowing how to avoid them can enhance mathematical accuracy and confidence. Below are some of the typical errors and strategies to prevent them.
1. Misinterpreting the Square Root Symbol
One common mistake is misinterpreting the square root symbol \( \sqrt{} \). For instance, assuming \( \sqrt{x^2 + y^2} = x + y \) is incorrect.
- Example: \( \sqrt{12^2 + 5^2} \neq 12 + 5 \). The correct calculation is \( \sqrt{144 + 25} = \sqrt{169} = 13 \).
- How to avoid: Always remember that the square root of a sum of squares is not the sum of the roots.
2. Incorrectly Adding Square Roots
Another frequent error is adding square roots incorrectly, such as assuming \( 3\sqrt{3} + 3 = 6\sqrt{3} \).
- Example: \( 3\sqrt{3} + 3 = 3(\sqrt{3} + 1) \).
- How to avoid: Only like terms can be added. \( a\sqrt{x} + b\sqrt{x} = (a + b)\sqrt{x} \).
3. Simplifying Products Incorrectly
Students often mistakenly simplify products involving square roots, such as \( (4a)^2 = 4a^2 \).
- Example: \( (4a)^2 = 4a \times 4a = 16a^2 \).
- How to avoid: Expand the expression fully to avoid mistakes.
4. Errors with Negative Numbers
Misunderstanding the squaring of negative numbers can lead to errors. For example, \( (-3)^2 = -9 \) is incorrect.
- Example: \( (-3)^2 = (-3) \times (-3) = 9 \).
- How to avoid: Remember that the square of a negative number is positive.
5. Miscalculating Small Decimals
Small decimal values can be tricky, leading to mistakes like \( 0.2^2 = 0.4 \).
- Example: \( 0.2^2 = 0.2 \times 0.2 = 0.04 \).
- How to avoid: Pay careful attention to decimal multiplication.
6. Incorrectly Dividing Square Roots
Incorrect division involving square roots, such as \( \sqrt{0.9} = \sqrt{9/10} = 3/\sqrt{10} \), is a common error.
- Example: \( \sqrt{0.09} = 0.3 \), not \( 3/\sqrt{10} \).
- How to avoid: Simplify the expression step-by-step to avoid confusion.
Being aware of these common mistakes and practicing correct methods can significantly improve accuracy when working with square roots.
Square Root Calculation Tools and Resources
Calculating square roots can be simplified with the use of various tools and resources available online. These tools not only provide accurate results but also help in understanding the process of square root calculation. Here are some useful tools and resources:
-
Online Calculators
- Symbolab: This online tool allows you to calculate square roots, providing step-by-step solutions for better understanding. You can visit their to explore more.
- Mathway: A versatile calculator that handles square roots along with other mathematical functions. It's user-friendly and offers detailed explanations. Check it out on .
- Omni Calculator: This platform offers a dedicated square root calculator which simplifies the calculation process and provides insights into the steps involved. Visit the page for more information.
-
Mobile Apps
- Photomath: This app allows users to take pictures of handwritten or printed math problems and provides instant solutions, including square roots.
- Mathway App: Available on various platforms, this app provides solutions to a wide range of math problems, including square roots, and offers step-by-step explanations.
-
Educational Websites
- Khan Academy: Offers comprehensive lessons and practice problems on square roots and other mathematical concepts. You can access it at .
- Math Is Fun: Provides clear explanations and interactive tools to understand and calculate square roots. Visit for more resources.
-
Graphing Tools
- Desmos: A powerful graphing calculator that helps visualize square root functions and other mathematical equations. Explore it at .
Using these tools and resources can greatly enhance your understanding and efficiency in calculating square roots. They provide not only the final answer but also the methodology, ensuring a deeper grasp of the concept.
Frequently Asked Questions
Understanding square roots can be challenging. Below are some common questions and detailed answers to help clarify these concepts.
1. What is a square root?
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4 because 4 × 4 = 16.
2. How do you find the square roots of numbers between 1 and 30?
You can find the square roots of numbers between 1 and 30 using methods such as:
- Prime Factorization: This involves breaking down a number into its prime factors and then pairing them to find the square root.
- Long Division: This is a manual arithmetic method that involves dividing the number to get closer to the square root step-by-step.
3. What are the perfect square numbers between 1 and 30?
The perfect square numbers between 1 and 30 are those that have integer square roots. They are:
- 1 (√1 = 1)
- 4 (√4 = 2)
- 9 (√9 = 3)
- 16 (√16 = 4)
- 25 (√25 = 5)
4. Why are square roots important in real life?
Square roots are used in various real-life applications such as in calculating areas, in the Pythagorean theorem for finding distances, and in various fields of science and engineering to solve quadratic equations and analyze physical phenomena.
5. Are there any tools to help calculate square roots?
Yes, several tools can assist with square root calculations, including:
- Online Calculators: Websites and apps offer quick and accurate square root calculations.
- Scientific Calculators: Physical calculators with a square root function are useful for manual computations.
- Mathematical Software: Software like MATLAB, Mathematica, and Python libraries can perform square root calculations and more complex mathematical operations.
6. What are some common mistakes when working with square roots?
Common mistakes include:
- Confusing square roots with squares. For example, mistaking √9 for 18 instead of 3.
- Forgetting that both positive and negative numbers can be square roots, e.g., √16 can be both 4 and -4.
- Not simplifying square roots properly when dealing with fractions or decimals.
By understanding these common pitfalls, you can avoid errors in your calculations and enhance your comprehension of square roots.
Conclusion and Further Reading
The study of square roots, especially those between 1 and 30, is fundamental in understanding various mathematical concepts. Square roots are not just abstract numbers; they have practical applications in areas such as geometry, physics, and engineering. Mastery of this topic can significantly enhance problem-solving skills and mathematical intuition.
As we explored the square roots of numbers from 1 to 30, we discovered the importance of perfect squares, the methodologies for calculating square roots, and their real-life applications. Visual representations help in comprehending the concepts more effectively, while being aware of common mistakes ensures accuracy in calculations.
For those eager to dive deeper into this subject, here are some recommended resources:
- : An online tool that helps calculate square roots quickly and accurately.
- : Offers detailed explanations and resources on square roots and other mathematical concepts.
- : Provides comprehensive tutorials and practice exercises on square roots and related topics.
Further study and practice can solidify your understanding and enable you to apply these concepts effectively in more advanced mathematical problems. Whether you are a student, teacher, or enthusiast, these resources can provide valuable insights and learning opportunities.
Continue exploring the fascinating world of mathematics and never hesitate to seek out additional resources and tools to aid in your learning journey. Happy studying!
Video hướng dẫn về căn bậc hai từ 1 đến 30 và cách viết các số chính phương từ 1 đến 30. Phù hợp với những ai muốn tìm hiểu về toán học cơ bản và các khái niệm liên quan đến căn bậc hai.
Căn Bậc Hai từ 1 đến 30/Viết Các Số Chính Phương từ 1 đến 30/Căn Bậc Hai
READ MORE:
Video hướng dẫn về căn bậc hai của các số từ 1 đến 30, bao gồm biểu đồ và các ví dụ minh họa. Phù hợp cho những ai muốn nắm vững kiến thức cơ bản về căn bậc hai trong toán học.
Căn Bậc Hai từ 1 Đến 30 | Toán Học Căn Bậc Hai | 1 Đến 30 Căn Bậc Hai | Biểu Đồ Căn Bậc Hai 1 Đến 30









