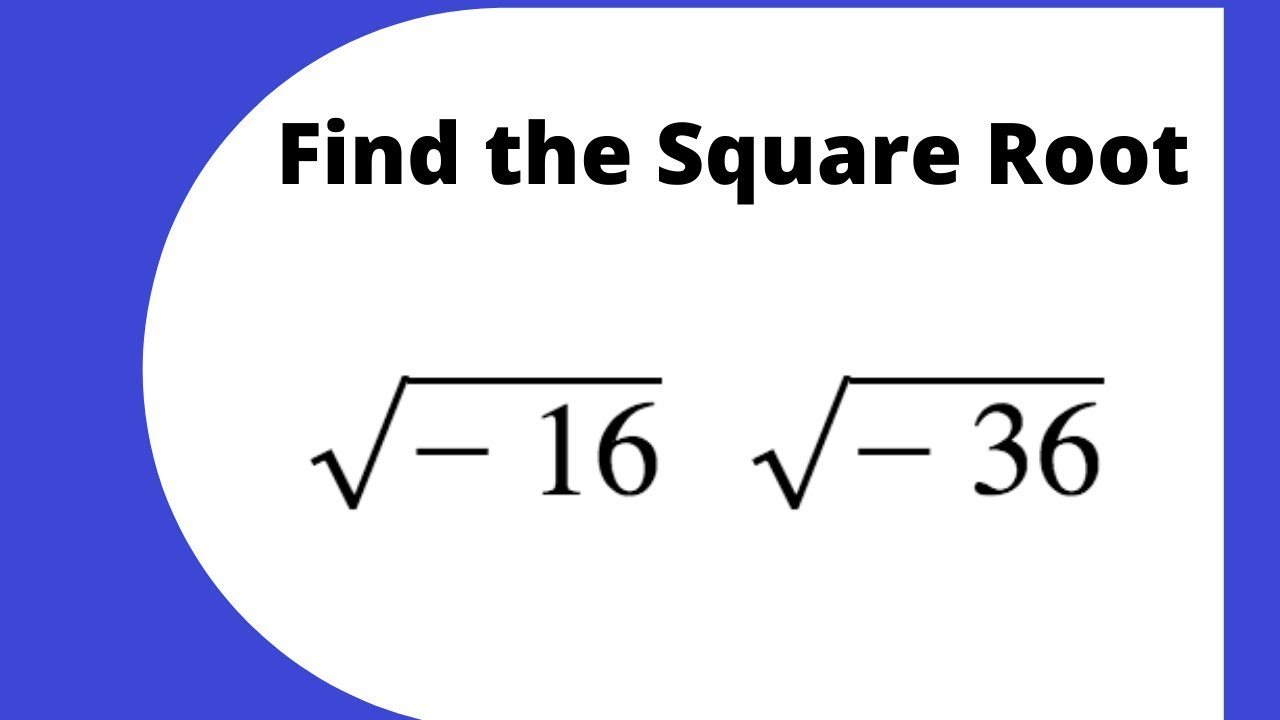Topic square root of 1 mil: Understanding the square root of 1 million can simplify many mathematical concepts. This article will explore how to calculate it, its significance, and practical applications. Whether you're a student or just curious, we'll make the square root of 1 mil easy to grasp.
Table of Content
- Square Root of 1 Million
- Introduction
- Definition and Basic Concept
- Calculating the Square Root of 1 Million
- Methods for Finding Square Roots
- Principal and Negative Square Roots
- Perfect Squares and Imperfect Squares
- Applications in Mathematics and Real Life
- Common Misconceptions and Errors
- Additional Resources and Tools
- YOUTUBE: Video hướng dẫn cách tính căn bậc hai từ 1 đến 1 triệu bằng mẹo siêu nhanh. Thích hợp cho người học toán và muốn tìm hiểu về các phương pháp tính toán nhanh.
Square Root of 1 Million
The square root of a number is a value that, when multiplied by itself, gives the original number. In this case, we want to find the square root of 1 million.
Calculation
The square root of 1 million (1,000,000) can be expressed as:
\[ \sqrt{1,000,000} = 1,000 \]
This is because \( 1,000 \times 1,000 = 1,000,000 \).
Properties of Square Roots
- Every positive real number has two square roots: one positive and one negative.
- The principal square root is the non-negative root, which is used in most calculations.
- The square root function is the inverse of squaring a number.
Example Calculations
| Number | Square Root |
|---|---|
| 81 | \( \sqrt{81} = \pm 9 \) |
| 25 | \( \sqrt{25} = \pm 5 \) |
| 100 | \( \sqrt{100} = \pm 10 \) |
| 10 | \( \sqrt{10} \approx \pm 3.162 \) |
Perfect Squares
Perfect squares are numbers that have integer square roots. Here are some examples:
- 4 is a perfect square because \( \sqrt{4} = 2 \).
- 9 is a perfect square because \( \sqrt{9} = 3 \).
- 16 is a perfect square because \( \sqrt{16} = 4 \).
- 25 is a perfect square because \( \sqrt{25} = 5 \).
Using Calculators
Various calculators can help you find square roots:
- Graphing Calculators: For example, the Texas Instruments TI-84 Plus can calculate the square root by pressing [2ND] and then [ √ ] followed by the number.
- Scientific Calculators: Typically have a square root button ( √ ) that can be used directly.
- Online Calculators: Websites like Mathway, CalculatorSoup, and OmniCalculator provide tools to find square roots and simplify radical expressions.
Conclusion
Calculating the square root of large numbers, like 1 million, is straightforward with the right tools. Remember that every positive number has two square roots, one positive and one negative, but the principal square root is usually the one used in calculations.

READ MORE:
Introduction
The square root of 1 million is a fundamental mathematical concept with significant implications in various fields of study and real-life applications. Understanding square roots, particularly that of 1 million, is crucial for students, educators, and professionals alike.
In this guide, we will delve into the concept of the square root, explore the methods used to calculate the square root of 1 million, and examine the properties and applications of square roots in mathematics and beyond. By the end of this guide, you will have a comprehensive understanding of the square root of 1 million, its principal and negative roots, and how this knowledge can be applied in different contexts.
We will also address common misconceptions and errors associated with square roots, providing you with the tools and resources needed to avoid these pitfalls. Whether you are a beginner or looking to deepen your mathematical knowledge, this guide is designed to be a thorough and accessible resource.
Definition and Basic Concept
The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical notation, the square root of a number \(a\) is denoted as \(\sqrt{a}\). For instance, the square root of 9 is 3, because \(3 \times 3 = 9\). This is expressed as \(\sqrt{9} = 3\).
In general, every nonnegative real number \(a\) has a unique nonnegative square root, known as the principal square root, which is denoted by \(\sqrt{a}\). The principal square root is always nonnegative, even though there can be another square root that is negative. For example, both 3 and -3 are square roots of 9 because \(3^2 = 9\) and \((-3)^2 = 9\). However, by convention, \(\sqrt{9} = 3\).
Square roots are particularly important in various fields of mathematics and science, as they help simplify complex equations and understand relationships between different quantities. They are also used in real-life applications such as calculating areas, volumes, and in various engineering and physics problems.
To find the square root of a number that is not a perfect square, approximation methods or calculators are usually used. One common method is the iterative approximation method, also known as Heron's method. This involves making an initial guess and then improving that guess through successive iterations until a satisfactory level of accuracy is reached.
Mathematically, the iterative process can be described as follows:
- Start with an initial guess \(x_0\) for \(\sqrt{a}\).
- Use the formula \(x_{n+1} = \frac{1}{2} \left( x_n + \frac{a}{x_n} \right)\) to get a new guess.
- Repeat step 2 until the difference between successive guesses is smaller than a desired tolerance level.
Understanding the basic concept of square roots is essential for delving into more advanced mathematical topics, including algebra, calculus, and beyond.
Calculating the Square Root of 1 Million
The square root of a number is a value that, when multiplied by itself, gives the original number. To find the square root of 1 million, we can use several methods. Below, we will explore the calculation step-by-step.
-
Understanding the Problem:
The mathematical representation of finding the square root of 1 million is:
\[ \sqrt{1000000} \]
-
Using Basic Square Roots:
We know that:
\[ 1000000 = 10^6 \]
Thus, the square root of 1 million can be found by taking the square root of \( 10^6 \):
\[ \sqrt{10^6} = 10^{6/2} = 10^3 = 1000 \]
Therefore, the square root of 1 million is 1000.
-
Verification:
To verify, we can square the result to check if we get back the original number:
\[ 1000 \times 1000 = 1000000 \]
This confirms that our calculation is correct.
-
Using a Calculator:
For more complex numbers, or to confirm our results, we can use a calculator:
- Enter the number (1000000) into the calculator.
- Press the square root (√) button.
- The calculator will display the result, which should be 1000.
-
Square Root Properties:
It’s important to note that every positive real number has two square roots: one positive and one negative. However, in most practical scenarios, we consider the principal (positive) square root:
\[ \sqrt{1000000} = \pm 1000 \]
For our purpose, we use the positive root.
Calculating square roots manually or using a calculator both affirm that the square root of 1 million is indeed 1000. This method can be applied to find the square roots of other perfect squares efficiently.
Methods for Finding Square Roots
Finding the square root of a number can be approached through several methods, each suited for different contexts and levels of precision required. Here are some of the most common methods:
- Prime Factorization: This method involves breaking down the number into its prime factors. If the number is a perfect square, group the factors into pairs and multiply one number from each pair.
- Example: To find the square root of 1,000,000, first express it as \(1,000,000 = 10^6\). Since \(10^6\) is a perfect square, its square root is \(10^3 = 1000\).
- Long Division Method: This is a manual, step-by-step method to find the square root. It is similar to long division and involves guessing and averaging.
- Group the digits of the number in pairs, starting from the decimal point.
- Find the largest number whose square is less than or equal to the first pair or single digit.
- Subtract this square from the first pair, bring down the next pair of digits, and repeat the process.
- Continue this process until you have the desired precision.
- Example: The square root of 1,000,000 using the long division method will consistently show that it simplifies to 1000.
- Using a Calculator: For quick and accurate results, use a scientific calculator. Enter the number and press the square root (√) button to get the result instantly.
- Example: Enter 1,000,000 in the calculator and press √ to get 1000.
- Newton's Method (Heron's Method): This iterative method approximates the square root by improving guesses.
- Start with an initial guess (e.g., \(x_0 = 500\) for \(\sqrt{1,000,000}\)).
- Use the formula: \(x_{n+1} = \frac{1}{2}\left( x_n + \frac{1,000,000}{x_n} \right)\) to get a better approximation.
- Repeat the process until the difference between successive approximations is negligible.
- Example: Iterating this method quickly converges to 1000.
- Approximation and Estimation: For rough estimates, use nearby perfect squares.
- Example: Knowing that \(\sqrt{1,000,000}\) lies between \(\sqrt{900,000} = 950\) and \(\sqrt{1,102,500} = 1050\), one can approximate \(\sqrt{1,000,000} \approx 1000\).
Each method has its applications, from educational purposes and quick calculations to high-precision requirements in scientific computations.
Principal and Negative Square Roots
The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\). For any positive real number \(x\), there are two square roots: one positive and one negative. These are known as the principal square root and the negative square root, respectively.
Mathematically, if \(x\) is a positive real number, then its square roots are denoted as:
- The principal square root: \( \sqrt{x} \)
- The negative square root: \(-\sqrt{x} \)
For example, the square roots of 25 are 5 and -5 because:
\(5^2 = 25\) and \((-5)^2 = 25\)
The principal square root is the non-negative root, and is often the default when referring to "the square root" of a number. This is important in many mathematical contexts to ensure consistency and clarity.
To illustrate further, consider the square root of 1,000,000:
- Principal square root: \( \sqrt{1000000} = 1000 \)
- Negative square root: \(-\sqrt{1000000} = -1000 \)
Both \(1000\) and \(-1000\) are valid square roots because:
\(1000^2 = 1000000\) and \((-1000)^2 = 1000000\)
In general, for any positive number \(a\):
\[ y = \pm\sqrt{a} \]
This notation means there are two solutions: one positive and one negative. When solving equations, it's crucial to consider both roots to capture all possible solutions.
For example, in solving the equation \(x^2 = 25\), the solutions are:
\[ x = \pm\sqrt{25} \]
Which simplifies to:
\[ x = \pm 5 \]
Thus, \(x\) can be either 5 or -5. Ignoring the negative root can lead to incomplete solutions in algebraic problems.
In summary, while the principal square root refers to the non-negative root by default, recognizing the existence of the negative root is essential for a comprehensive understanding of square roots.
Perfect Squares and Imperfect Squares
In mathematics, understanding the difference between perfect squares and imperfect squares is essential for various applications.
Perfect Squares
A perfect square is an integer that is the square of another integer. This means it can be expressed as the product of an integer with itself. For example, \(1, 4, 9, 16,\) and \(25\) are perfect squares because:
- \(1 = 1 \times 1 = 1^2\)
- \(4 = 2 \times 2 = 2^2\)
- \(9 = 3 \times 3 = 3^2\)
- \(16 = 4 \times 4 = 4^2\)
- \(25 = 5 \times 5 = 5^2\)
The properties of perfect squares include:
- They are always non-negative.
- The square root of a perfect square is always an integer.
- They can be geometrically represented as a square with integer side lengths.
Imperfect Squares
An imperfect square, on the other hand, is a number that is not a perfect square. The square root of an imperfect square is not an integer and is usually an irrational number. Examples of imperfect squares include \(2, 3, 5, 6,\) and \(7\) because their square roots are not whole numbers.
For instance:
- \(\sqrt{2} \approx 1.414\)
- \(\sqrt{3} \approx 1.732\)
- \(\sqrt{5} \approx 2.236\)
Identifying Perfect and Imperfect Squares
There are a few methods to determine if a number is a perfect square:
- Prime Factorization Method: Factorize the number into its prime factors. If all prime factors can be paired, then the number is a perfect square.
- Square Root Method: Calculate the square root of the number. If the result is an integer, then it is a perfect square.
- Digit Pattern: Perfect squares have specific digit patterns. For example, a number ending in 2, 3, 7, or 8 cannot be a perfect square.
Examples and Applications
Perfect squares are used in various mathematical contexts, such as simplifying radicals and solving quadratic equations. They are also useful in geometry for calculating areas.
Here is a table listing some perfect and imperfect squares:
| Number | Square Root | Perfect Square? |
|---|---|---|
| 49 | 7 | Yes |
| 50 | \(\approx 7.071\) | No |
| 64 | 8 | Yes |
| 65 | \(\approx 8.062\) | No |
Understanding the distinction between perfect and imperfect squares can significantly aid in problem-solving and mathematical reasoning.
Applications in Mathematics and Real Life
Square roots have a wide range of applications in both mathematics and real life. Understanding these applications can help highlight the importance of this fundamental mathematical concept.
Mathematics Applications
-
Pythagorean Theorem:
Square roots are used to calculate the length of the hypotenuse of a right triangle. According to the Pythagorean Theorem, for a right triangle with sides \(a\) and \(b\) and hypotenuse \(c\):
\[c = \sqrt{a^2 + b^2}\]
-
Quadratic Equations:
Square roots are integral in solving quadratic equations using the quadratic formula:
\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
-
Distance Formula:
Square roots are used to calculate the distance between two points in a 2-dimensional or 3-dimensional space. The distance \(D\) between points \((x_1, y_1)\) and \((x_2, y_2)\) is:
\[D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\]
For three-dimensional space, the formula extends to:
\[D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}\]
Real Life Applications
-
Construction and Engineering:
Square roots are used to calculate various measurements, such as the length of the diagonal support in construction projects. For example, if the area of a square is given, the length of a side can be found using the square root.
-
Physics and Gravity:
Square roots are used to determine the time it takes for an object to fall to the ground under gravity. For an object dropped from a height \(h\), the time \(t\) to reach the ground is given by:
\[t = \frac{\sqrt{h}}{4}\]
-
Finance:
In finance, square roots are used to calculate the rate of return on an investment over a given period. The formula involving square roots can help in determining the annualized return rate.
-
Accident Investigation:
Square roots are used by police to determine the speed of a car before braking based on the length of skid marks. The formula used is:
\[\text{Speed} = \sqrt{24 \times \text{Skid Mark Length}}\]
These applications demonstrate the versatility and importance of square roots in various fields, making them an essential mathematical tool.
Common Misconceptions and Errors
Understanding the common misconceptions and errors related to square roots is essential for avoiding mistakes and deepening comprehension. Below are some typical errors and misunderstandings along with clarifications and strategies to avoid them.
- Confusing the Principal and Negative Square Roots:
Many students assume that the square root of a number is always positive. The principal square root of a positive number is indeed positive, but each positive number actually has two square roots: one positive and one negative. For example:
- \(\sqrt{25} = 5\)
- \(-\sqrt{25} = -5\)
It’s important to note both when solving equations.
- Misapplying Square Root Properties:
Another common error is misapplying properties of square roots. For instance, assuming \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\) is incorrect. The correct property is:
- \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
Understanding the correct properties can prevent these mistakes.
- Neglecting to Consider Both Solutions:
When solving quadratic equations, students often forget to consider both the positive and negative roots. For example, solving \(x^2 = 25\) yields:
- \(x = 5\)
- \(x = -5\)
Both solutions should be considered in the final answer.
- Incorrectly Simplifying Radical Expressions:
Simplifying square roots incorrectly is another frequent error. For example, simplifying \(\sqrt{50}\) as \(5\sqrt{2}\) instead of the correct \(5\sqrt{2}\) or \(\sqrt{25 \cdot 2}\) as \(5\sqrt{2}\).
Proper understanding of prime factorization helps in correctly simplifying radicals.
- Errors in Handling Square Roots in Equations:
When isolating variables, students might mishandle the square root operation, forgetting to square both sides of an equation. For instance, solving \(\sqrt{x} = 3\) should correctly be:
- Squaring both sides: \(x = 3^2\)
- Resulting in: \(x = 9\)
By addressing these misconceptions and applying correct mathematical principles, students can avoid common errors and improve their understanding of square roots.

Additional Resources and Tools
To further explore and master the concept of square roots, especially in the context of 1 million, various resources and tools are available online. These can help enhance understanding and provide practice through interactive activities, games, and comprehensive guides.
- Online Calculators:
Online square root calculators allow for quick and easy calculations of square roots. These tools are particularly useful for checking manual calculations or performing quick computations. Some popular online calculators include:
- Mathway
- Symbolab
- WolframAlpha
- Interactive Games:
Engage in interactive and fun learning with online games designed to practice square roots. These games often combine educational content with entertaining elements to make learning more enjoyable.
- - Practice square roots by selecting the correct marble.
- - Guide the MathPup to hit the correct number bubble.
- - Solve problems based on irrational square roots or surds.
- - Customizable game for practicing square root calculations.
- - Match numbers and their square roots to complete the grid.
- Educational Worksheets:
Printable worksheets offer structured practice and can be used for self-study or in a classroom setting. They provide a variety of problems that reinforce the understanding of square roots through repetitive practice.
- Homeschool Den - Provides a variety of worksheets and activities tailored for different learning levels.
- Khan Academy - Offers comprehensive lessons and practice problems on square roots and related topics.
- Interactive Tutorials:
Websites with interactive tutorials and video lessons can be very effective for visual and auditory learners. These resources break down complex concepts into easy-to-understand steps.
- Khan Academy - Extensive video tutorials on square roots and other mathematical concepts.
- Coursera and Udemy - Platforms offering courses that cover square roots as part of broader mathematics curricula.
These resources and tools can greatly enhance your understanding and proficiency in working with square roots, providing both foundational knowledge and advanced practice opportunities.
Video hướng dẫn cách tính căn bậc hai từ 1 đến 1 triệu bằng mẹo siêu nhanh. Thích hợp cho người học toán và muốn tìm hiểu về các phương pháp tính toán nhanh.
Căn Bậc Hai Từ 1 Đến 1000000 | 1 TRIỆU | MẸO SIÊU NHANH. SỐ ĐẶC BIỆT 6 CHỮ SỐ
READ MORE:
Học cách tính căn bậc hai của một phân số là số chính phương, ví dụ 7, căn(1/100)