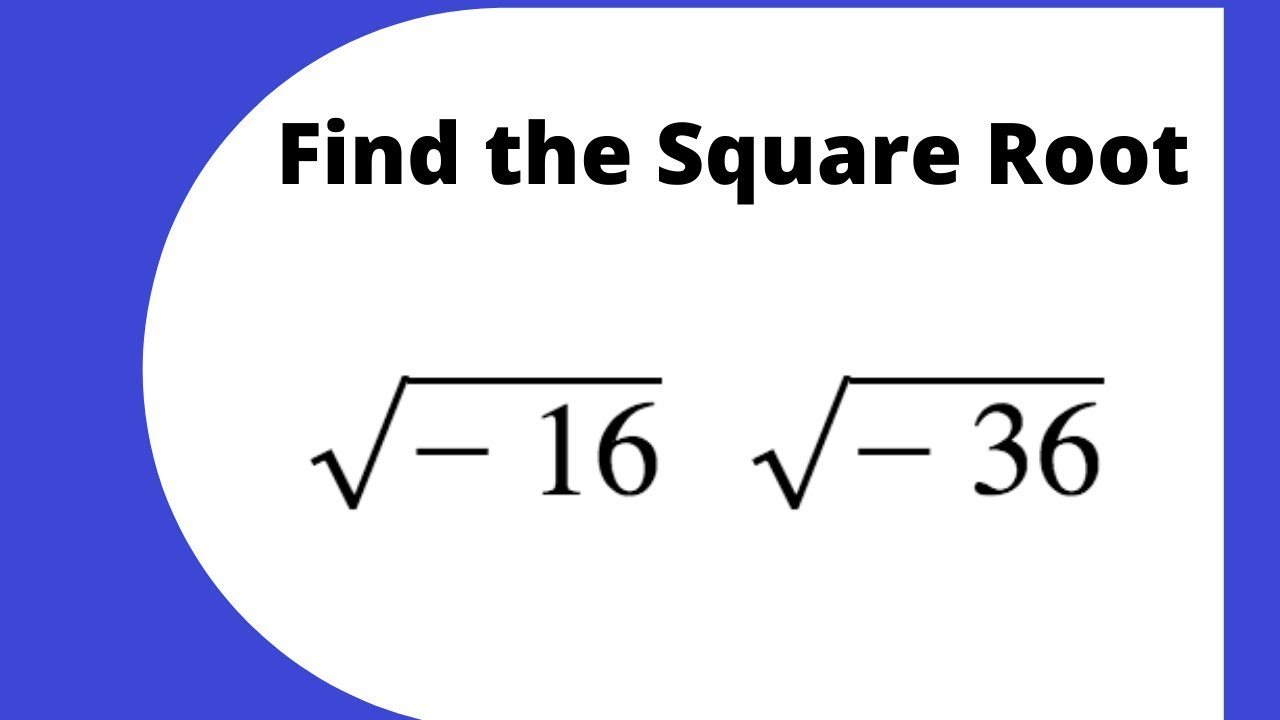Topic the square root of 1: The square root of 1 is a fundamental mathematical concept with both real and imaginary implications. This article explores the properties, applications, and interesting facts about the square root of 1, making it accessible and engaging for readers of all levels.
Table of Content
- Understanding the Square Root of 1
- Introduction
- Definition and Basic Properties
- Derivation of the Square Root of 1
- Complex Numbers and Square Roots
- Square Root Symbol and Notation
- Perfect Squares and Their Roots
- Calculating Square Roots
- Applications of Square Roots
- Interesting Facts
- Conclusion
- YOUTUBE: Tìm hiểu về căn bậc hai của -1 trong video này. Khám phá sự thú vị của số ảo và ứng dụng của chúng trong toán học và khoa học.
Understanding the Square Root of 1
The square root of 1 is a fundamental concept in mathematics. It is a value that, when multiplied by itself, yields the number 1.
Mathematical Definition
Mathematically, the square root of 1 is represented as:
\[\sqrt{1} = 1\]
This is because \(1 \times 1 = 1\). However, it's important to note that -1 is also a square root of 1 because:
\[(-1) \times (-1) = 1\]
Properties of Square Roots
- Every positive number has two square roots: a positive and a negative root.
- For the number 1, the square roots are 1 and -1.
- The principal square root is the non-negative root, which is 1 in this case.
Derivation of Square Root of 1
The derivation can be understood through a simple quadratic equation:
Let \(x\) be the square root of 1. Then:
\[x^2 = 1\]
This quadratic equation has two solutions:
- \[x = 1\]
- \[x = -1\]
Therefore, the square root of 1 is both 1 and -1. Typically, the positive root is considered in most contexts.
Table of Square Roots from 1 to 10
| Number | Square Root |
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3 |
| 10 | 3.162 |
Visualizing Square Roots
Visualizing square roots can help in understanding the concept better. For example, the number 1 lies at the intersection of two lines on a graph, representing both its positive and negative square roots.
In conclusion, the square root of 1 is a simple yet essential concept in mathematics with the principal square root being 1 and the other root being -1. This concept is foundational and helps in solving various mathematical problems.

READ MORE:
Introduction
Understanding the square root of 1 is fundamental in mathematics. The square root of a number is a value that, when multiplied by itself, gives the original number. For the number 1, its square root is 1, since 1 × 1 = 1. This concept extends to both positive and negative values, with -1 also being a square root of 1 as (-1) × (-1) = 1.
Square roots are commonly represented by the radical symbol "√". When dealing with positive numbers, the square root is straightforward, but with negative numbers, we enter the realm of complex numbers, where the square root of -1 is denoted as "i", the imaginary unit.
Calculating square roots can be done using various methods, such as factorization for perfect squares or long division for non-perfect squares and larger numbers. These methods are essential for solving mathematical problems efficiently.
The square root concept is not limited to integers; it also applies to decimal numbers and can be approximated using calculators or iterative methods for more accuracy. Mastery of square roots is crucial for higher mathematical studies and practical applications.
Definition and Basic Properties
The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 1 is a number y such that y² = 1. This means both 1 and -1 are square roots of 1 since 1² = 1 and (-1)² = 1.
There are several important properties of square roots:
- The square root of 1 is denoted as √1 or 11/2.
- Every positive number has two square roots: a positive root and a negative root, often represented as ±√x.
- The principal square root is the non-negative root, which for 1 is simply 1.
- The concept of square roots extends to negative numbers within the framework of complex numbers, where the square root of -1 is represented as the imaginary unit i, with i² = -1.
Square roots are fundamental in various mathematical contexts, including solving quadratic equations, understanding geometric concepts, and working with complex numbers. The properties of square roots are used extensively in algebra, calculus, and other fields of mathematics.
Derivation of the Square Root of 1
The square root of 1 is a fundamental concept in mathematics. This derivation involves understanding the properties and definitions of square roots and their applications in various mathematical contexts.
Let's start with the basic definition:
The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\). For the number 1, this means finding \(y\) such that:
\[
y^2 = 1
\]
We see that both \(y = 1\) and \(y = -1\) satisfy this equation because:
- \(1^2 = 1\)
- \((-1)^2 = 1\)
Therefore, the square root of 1 can be expressed as:
\[
\sqrt{1} = \pm 1
\]
This indicates that the square root of 1 has two solutions: 1 and -1. However, in most contexts, especially in principal square roots, the positive solution is often considered, so:
\[
\sqrt{1} = 1
\]
In complex number theory, the derivation and implications extend further, but for real numbers, the above derivation holds.
Understanding this basic derivation helps in simplifying more complex mathematical expressions and solving various algebraic equations involving square roots.
Complex Numbers and Square Roots
Understanding the square root of a number, especially in the realm of complex numbers, involves several key concepts and mathematical techniques. Here's a detailed overview of complex numbers and their square roots.
- Definition of Complex Numbers
- A complex number is expressed in the form \( z = a + bi \), where \( a \) and \( b \) are real numbers, and \( i \) is the imaginary unit satisfying \( i^2 = -1 \).
- Square Roots of Real Numbers
- The square root of a real number \( x \) is a number \( y \) such that \( y^2 = x \). For positive real numbers, there are two square roots: \( \sqrt{x} \) and \( -\sqrt{x} \).
- Square Roots of Complex Numbers
- The square root of a complex number involves finding a complex number \( w \) such that \( w^2 = z \), where \( z \) is the given complex number.
- Using polar coordinates, a complex number \( z \) can be represented as \( z = re^{i\theta} \), where \( r \) is the magnitude and \( \theta \) is the argument.
- By De Moivre's Theorem, the square roots of a complex number can be derived as follows:
- If \( z = re^{i\theta} \), then the square roots of \( z \) are given by \( \sqrt{z} = \sqrt{r} e^{i(\theta/2 + k\pi)} \) for \( k = 0, 1 \).
| Step | Details |
|---|---|
| 1 | Convert the complex number to its polar form. |
| 2 | Apply De Moivre's Theorem to find the roots. |
| 3 | Convert the roots back to rectangular form if needed. |
This process reveals that every complex number has two square roots, which are complex conjugates of each other. Understanding these fundamentals aids in comprehending more advanced topics in complex analysis and engineering.

Square Root Symbol and Notation
The square root symbol, denoted as \( \sqrt{} \), is used in mathematics to represent the principal (non-negative) square root of a number. For example, \( \sqrt{4} = 2 \), because \( 2^2 = 4 \). The notation evolved over time, with the modern radical symbol being first used by the German mathematician Christoff Rudolff in 1525, and later refined by René Descartes in 1637 to include the vinculum (the horizontal bar).
In general, the square root of a number \( a \) is denoted as:
\[ \sqrt{a} \]
For any non-negative number \( a \), the expression \( \sqrt{a} \) represents the number \( x \) such that \( x^2 = a \). Notably, every positive real number has two square roots: one positive and one negative. The principal square root is always non-negative.
Some key points about the square root symbol and its notation include:
- The radical symbol (√) represents the square root.
- The expression inside the radical symbol is called the radicand.
- The radical symbol can be extended to represent the \( n \)-th root, denoted as \( \sqrt[n]{a} \).
- Unicode and HTML character codes for the square root symbol are: \(\sqrt{}\) U+221A, `√`, or `√`.
Below is a table summarizing the notation for various roots:
| Root | Symbol | Example |
|---|---|---|
| Square Root | \( \sqrt{} \) | \( \sqrt{16} = 4 \) |
| Cube Root | \( \sqrt[3]{} \) | \( \sqrt[3]{27} = 3 \) |
| Fourth Root | \( \sqrt[4]{} \) | \( \sqrt[4]{81} = 3 \) |
Using these notations, mathematicians can succinctly express roots of numbers, which are fundamental in various branches of mathematics and its applications.
Perfect Squares and Their Roots
A perfect square is a number that is the square of an integer. The square root of a perfect square is always an integer. Here are some common perfect squares and their roots:
| Perfect Square | Square Root |
| 0 | 0 |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
Perfect squares are fundamental in mathematics because they simplify the process of taking square roots. The concept can be extended to negative numbers, where the square of a negative number results in a positive perfect square. For example, \( (-5)^2 = 25 \).
The understanding of perfect squares and their roots is crucial for solving quadratic equations and for various applications in geometry and algebra.
Calculating Square Roots
Calculating the square root of a number involves finding a value which, when multiplied by itself, equals the original number. While the square roots of perfect squares like 1, 4, 9, and 16 are integers, finding the square roots of non-perfect squares requires more advanced methods.
Here are some common methods used to calculate square roots:
1. Using a Calculator
The simplest and most straightforward method is to use a calculator with a square root function (√). This method provides quick and accurate results for any number.
2. Estimation and Refinement
For manual calculation, estimation and refinement can be used. This involves making an initial guess and then refining that guess through iterations. For example, to find √10:
- Start with an initial guess (e.g., 3.5).
- Divide the number (10) by the guess (3.5), yielding approximately 2.857.
- Averaging the guess and the result: (3.5 + 2.857) / 2 ≈ 3.1785.
- Repeat the process using 3.1785 as the new guess.
3. Newton's Method (Iterative Method)
Newton's Method, also known as the Newton-Raphson method, provides a systematic approach to finding square roots. The iterative formula is:
\[ x_{k+1} = \frac{1}{2} \left( x_k + \frac{n}{x_k} \right) \]
Where \( x_k \) is the current guess and \( n \) is the number whose square root is being calculated. Here's how to apply it for √10:
- Choose an initial guess (e.g., \( x_0 = 3 \)).
- Apply the formula: \( x_1 = \frac{1}{2} \left( 3 + \frac{10}{3} \right) = 3.1667 \).
- Repeat the process: \( x_2 = \frac{1}{2} \left( 3.1667 + \frac{10}{3.1667} \right) ≈ 3.1623 \).
Continue iterating until the desired level of accuracy is reached.
4. Prime Factorization
For perfect squares, prime factorization can be a useful method. This involves breaking down the number into its prime factors and pairing them. For example, to find the square root of 144:
- Prime factorize 144: \( 144 = 2^4 \times 3^2 \).
- Take the square root of each factor: \( \sqrt{144} = \sqrt{2^4} \times \sqrt{3^2} = 2^2 \times 3 = 4 \times 3 = 12 \).
These methods provide a variety of ways to calculate square roots, from simple estimation to more precise iterative techniques, ensuring that you can find square roots whether or not you have access to a calculator.
Applications of Square Roots
Square roots have a wide range of applications across various fields, demonstrating their fundamental importance in both theoretical and practical contexts. Below are some of the key applications:
- Geometry and Area Calculations: In geometry, the square root is used to determine the side length of a square given its area. For example, if the area of a square is \(A\) square units, the length of each side is \(\sqrt{A}\) units. This principle is essential for solving problems related to area and perimeter calculations in various shapes.
- Physics and Gravity: The time it takes for an object to fall from a certain height can be calculated using square roots. For instance, on Earth, the time \(t\) in seconds for an object to fall from a height \(h\) feet is given by \(t = \frac{\sqrt{h}}{4}\). This application is critical in understanding motion under gravity.
- Accident Investigations: In accident investigations, police officers use square roots to determine the speed of a vehicle before it applied brakes based on the length of the skid marks. The formula often used is \(v = \sqrt{24d}\), where \(v\) is the speed in miles per hour and \(d\) is the length of the skid marks in feet.
- Finance: In finance, the square root is used to calculate the volatility of a stock's price, which is a measure of the risk associated with the investment. The calculation involves taking the square root of the variance of the stock's returns.
- Engineering and Architecture: Engineers use square roots to determine the natural frequencies of structures like bridges and buildings. These frequencies help predict how structures will react to various loads, such as wind or traffic, ensuring their stability and safety.
- Statistics: Square roots are integral to statistical analysis, particularly in calculating the standard deviation, which is the square root of the variance. This measure helps in understanding the dispersion of data points in a dataset.
- Computer Science and Cryptography: Square roots are used in algorithms for encryption and data security, such as in the generation of public and private keys. They are also used in computer graphics to calculate distances and in game physics to simulate realistic movements.
- Navigation: In navigation, square roots help calculate the distance between two points on a map, essential for plotting accurate courses and bearings, especially in aviation and maritime contexts.
- Electrical Engineering: Square roots are used to compute power, voltage, and current in electrical circuits. These calculations are vital for designing and analyzing electrical systems and devices.
- Photography: The aperture of a camera lens, which controls the amount of light entering the camera, is related to the f-number. The area of the aperture is proportional to the square of the f-number, affecting the exposure and depth of field in photography.
These examples illustrate the diverse and critical roles that square roots play in various scientific, engineering, and everyday applications, underscoring their importance in understanding and solving real-world problems.

Interesting Facts
Here are some fascinating facts about square roots that highlight their importance and unique properties:
- The square root of a number is a value that, when multiplied by itself, gives the original number. For example, \(\sqrt{4} = 2\) because \(2 \times 2 = 4\).
- Imaginary numbers, such as the square root of -1, play a crucial role in mathematics. The square root of -1 is denoted as \(i\), which is the basis of complex numbers.
- The square root of 2 is an irrational number, approximately 1.41421. It represents the length of the diagonal of a square with sides of length 1.
- The concept of square roots dates back to ancient civilizations. For example, the Babylonians used methods to approximate square roots as early as 1900 BC.
- In digital imaging, cameras store the square roots of pixel brightness values to enhance image processing and display.
- The radical symbol (√) used to denote square roots was introduced by the mathematician Christoph Rudolff in 1525.
- Euler's identity, \(e^{i\pi} + 1 = 0\), involves the imaginary unit \(i\), demonstrating the deep connection between exponential functions and trigonometry.
- Square Root Day is celebrated on dates where both the day and the month are the square roots of the last two digits of the year, such as 4/4/16 (April 4, 2016).
- The golden ratio, approximately 1.618, can be expressed using square roots: \((1 + \sqrt{5}) / 2\).
- There is a lesser-known algorithm for manually calculating square roots that is not typically taught in schools, involving iterative approximation techniques.
Conclusion
In conclusion, the square root of 1, though appearing simple, serves as a foundational element in mathematics. Its study is not only essential for understanding basic arithmetic but also pivotal in more advanced mathematical fields, including algebra and calculus.
The concept of the square root extends far beyond just the number 1, encompassing a wide range of applications in various scientific and engineering disciplines. Square roots help in solving quadratic equations, analyzing signals in engineering, and even in financial modeling where they are used to calculate standard deviation and risk assessments.
Understanding square roots also introduces students to the fascinating world of irrational numbers and complex numbers, broadening their appreciation of the diversity and depth of mathematics. The simplicity of the square root of 1, resulting in both 1 and -1, exemplifies the dual nature of solutions in mathematics, reflecting the balance and symmetry inherent in mathematical principles.
In summary, mastering the square root of 1 opens doors to more advanced topics and applications, making it a critical stepping stone in the mathematical journey. Its presence in theoretical and practical contexts underscores its significance, making it a fundamental concept worth exploring in depth.
Tìm hiểu về căn bậc hai của -1 trong video này. Khám phá sự thú vị của số ảo và ứng dụng của chúng trong toán học và khoa học.
Căn Bậc Hai Của -1 Là Gì?
READ MORE:
Khám phá về căn bậc hai của số âm một trong video này. Tìm hiểu về số ảo và ứng dụng của chúng trong toán học và khoa học.
Căn Bậc Hai Của Số Âm Một