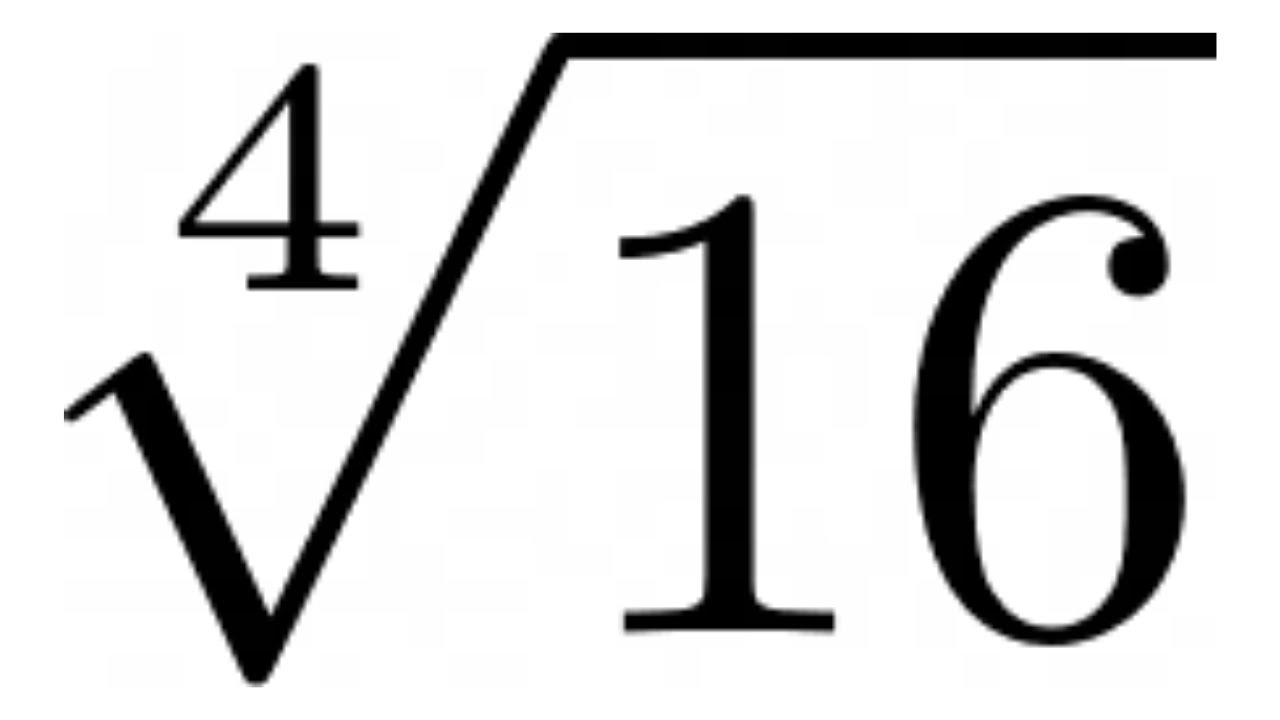Topic square root of half: Discover the methods to simplify the square root of half, an essential mathematical concept. This article explores the step-by-step process of simplifying √(1/2), its representation, and practical applications in various fields. Enhance your mathematical knowledge and skills with easy-to-follow explanations and examples.
Table of Content
- Understanding the Square Root of 1/2
- Introduction
- Mathematical Explanation
- Steps to Simplify Square Roots
- Square Root of Fractions
- Calculations and Examples
- Applications in Algebra
- Properties of Square Roots
- Square Root in Decimal Form
- Rationalizing the Denominator
- YOUTUBE: Khám phá lý do tại sao 'x mũ một phần hai' có nghĩa là căn bậc hai qua video này.
Understanding the Square Root of 1/2
The square root of 1/2 can be represented in various mathematical forms and has applications in different areas of mathematics.
Exact Form
The exact form of the square root of 1/2 is:
\[
\sqrt{\frac{1}{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]
Decimal Form
The decimal form of the square root of 1/2 is approximately:
\[
\frac{\sqrt{2}}{2} \approx 0.7071
\]
Steps to Simplify the Square Root of 1/2
- Start with the expression: \(\sqrt{\frac{1}{2}}\)
- Rewrite it as: \(\frac{1}{\sqrt{2}}\)
- Rationalize the denominator by multiplying by \(\frac{\sqrt{2}}{\sqrt{2}}\):
\[
\frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2}
\]
Calculating Square Roots Manually
To manually estimate the square root of a number, such as 1/2, follow these steps:
- Estimate a number \(b\).
- Divide the number (0.5) by \(b\). If the result is precise to the desired decimal place, stop.
- Average \(b\) and the result from step 2, and use this as the new guess.
- Repeat step 2 until the desired precision is achieved.
Applications
- Geometry: Calculating distances and angles.
- Physics: Understanding wave functions and other physical phenomena.
- Engineering: Solving problems involving roots and exponents.
| Form | Representation |
| Exact Form | \(\frac{\sqrt{2}}{2}\) |
| Decimal Form | 0.7071 |
Understanding the square root of 1/2 is essential for various mathematical and scientific applications, and it can be expressed in both exact and decimal forms for different uses.

READ MORE:
Introduction
The square root of half, often represented as \( \sqrt{\frac{1}{2}} \), is a concept that frequently appears in various mathematical contexts, including algebra, geometry, and physics. This value can be expressed in multiple forms and simplified using several steps. Understanding how to simplify \( \sqrt{\frac{1}{2}} \) is essential for solving more complex mathematical problems. This introduction provides a comprehensive look at the steps involved in simplifying \( \sqrt{\frac{1}{2}} \), including rewriting it in a simpler form and understanding its significance in different mathematical scenarios.
- Rewriting the Expression: \( \sqrt{\frac{1}{2}} \) can be rewritten using the property of radicals as \( \frac{\sqrt{1}}{\sqrt{2}} \).
- Simplifying the Numerator and Denominator: Since \( \sqrt{1} = 1 \), the expression becomes \( \frac{1}{\sqrt{2}} \).
- Rationalizing the Denominator: To remove the radical from the denominator, multiply the numerator and the denominator by \( \sqrt{2} \), resulting in \( \frac{\sqrt{2}}{2} \).
- Final Simplified Form: The simplified form of \( \sqrt{\frac{1}{2}} \) is \( \frac{\sqrt{2}}{2} \), which can also be represented as approximately 0.7071 in decimal form.
This step-by-step approach not only simplifies the expression but also ensures a deeper understanding of the process involved in manipulating radicals. This foundational knowledge is critical for students and professionals who engage with mathematical problems regularly.
Mathematical Explanation
The square root of half, represented as \(\sqrt{\frac{1}{2}}\), can be simplified using the properties of radicals. To begin, we use the rule for the square root of a fraction:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]
Applying this rule, we get:
\[
\sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}}
\]
Next, we rationalize the denominator to eliminate the square root from the denominator. This involves multiplying both the numerator and the denominator by \(\sqrt{2}\):
\[
\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]
Thus, the simplified form of \(\sqrt{\frac{1}{2}}\) is \(\frac{\sqrt{2}}{2}\). In decimal form, this value is approximately 0.7071.
To summarize:
- The initial expression: \(\sqrt{\frac{1}{2}}\)
- Applying the square root rule: \(\frac{1}{\sqrt{2}}\)
- Rationalizing the denominator: \(\frac{\sqrt{2}}{2}\)
- Decimal approximation: 0.7071
Steps to Simplify Square Roots
The process of simplifying square roots involves a few methodical steps. Simplifying a square root means rewriting it in the simplest form without a radical in the denominator. Here's a step-by-step guide:
-
Identify Perfect Squares:
Look for perfect square factors in the number under the square root. For instance, if simplifying \(\sqrt{18}\), note that 18 can be factored into \(9 \times 2\), where 9 is a perfect square.
-
Rewrite Using Factors:
Express the square root as a product of square roots: \(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2}\).
-
Simplify the Perfect Square:
Simplify the square root of the perfect square: \(\sqrt{9} = 3\). Thus, \(\sqrt{18} = 3\sqrt{2}\).
-
Rationalize the Denominator (if necessary):
If the simplified form has a square root in the denominator, multiply both the numerator and the denominator by the square root in the denominator to rationalize it. For example, \(\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\).
-
Combine and Simplify:
Combine like terms if possible and ensure the expression is in its simplest form. For example, \(\sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2}\).
By following these steps, you can simplify square roots efficiently and accurately. This approach helps in solving more complex mathematical problems that involve radicals.
Square Root of Fractions
Finding the square root of a fraction involves a few steps, which can be simplified using the properties of square roots and fractions. Let's explore the process with an example: the square root of 1/2.
Steps to Simplify Square Roots of Fractions
- Express the fraction under the square root as the square root of the numerator divided by the square root of the denominator:
\[
\sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}}
\] - Simplify the square roots of the numerator and the denominator:
\[
\sqrt{1} = 1 \quad \text{and} \quad \sqrt{2} = \sqrt{2}
\]Thus, the expression becomes:
\[
\frac{1}{\sqrt{2}}
\] - Rationalize the denominator by multiplying the numerator and the denominator by \(\sqrt{2}\):
\[
\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]Therefore, the square root of 1/2 is:
\[
\sqrt{\frac{1}{2}} = \frac{\sqrt{2}}{2}
\]
Square Root of Common Fractions
Here are some examples of square roots of common fractions:
- \[ \sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2} \]
- \[ \sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4} \]
- \[ \sqrt{\frac{25}{36}} = \frac{\sqrt{25}}{\sqrt{36}} = \frac{5}{6} \]
General Formula
In general, for any positive fractions \(\frac{a}{b}\), the square root can be expressed as:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]
Decimal Form
If you need the decimal form of the square root of a fraction, you can find the decimal equivalents of the square roots of the numerator and the denominator and then divide them:
For example, \(\sqrt{\frac{1}{2}}\) in decimal form is approximately 0.7071.

Calculations and Examples
The square root of a fraction can be calculated by finding the square root of the numerator and the square root of the denominator separately. This is because the square root function is multiplicative, meaning that √(a/b) = √a / √b.
Let's take the fraction 1/2 and calculate its square root step by step:
- Step 1: Identify the numerator and the denominator.
- Step 2: Calculate the square root of the numerator: √1 = 1.
- Step 3: Calculate the square root of the denominator: √2 ≈ 1.414.
- Step 4: Combine the results: √(1/2) = 1 / 1.414 ≈ 0.707.
Here is a detailed example to illustrate the calculations:
| Fraction | Numerator | Denominator | Square Root of Numerator | Square Root of Denominator | Result |
|---|---|---|---|---|---|
| 1/2 | 1 | 2 | 1 | 1.414 | 0.707 |
Let's verify the result by squaring it:
\[
(0.707)^2 = 0.707 \times 0.707 \approx 0.5
\]
This confirms that our calculation of √(1/2) = 0.707 is accurate.
We can generalize this method for any fraction a/b as follows:
- Find √a and √b separately.
- Divide √a by √b to get the result.
Let's consider another example with the fraction 4/9:
- Step 1: Identify the numerator and the denominator: 4 and 9.
- Step 2: Calculate the square root of the numerator: √4 = 2.
- Step 3: Calculate the square root of the denominator: √9 = 3.
- Step 4: Combine the results: √(4/9) = 2 / 3 = 0.666.
Verification by squaring:
\[
(0.666)^2 = 0.666 \times 0.666 \approx 0.444
\]
Since 0.444 is approximately equal to 4/9, our calculation is verified.
These examples demonstrate the process of finding the square root of fractions and verifying the results, ensuring accuracy in mathematical calculations.
Applications in Algebra
The square root of half, denoted as \( \sqrt{\frac{1}{2}} \) or \( \frac{\sqrt{2}}{2} \), is commonly encountered in algebra. It plays a vital role in various algebraic equations and transformations. Below are some key applications:
- Solving Quadratic Equations:
In quadratic equations of the form \( ax^2 + bx + c = 0 \), the square root of half can appear when solving for the roots using the quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \). If the discriminant \( (b^2 - 4ac) \) includes fractions, the square root of half may be part of the solution.
Example:
- Consider the quadratic equation \( x^2 - x - \frac{1}{2} = 0 \).
- Using the quadratic formula: \( x = \frac{1 \pm \sqrt{1 + 2}}{2} = \frac{1 \pm \sqrt{3}}{2} \).
- The roots are \( x = \frac{1 + \sqrt{3}}{2} \) and \( x = \frac{1 - \sqrt{3}}{2} \).
- Simplifying Expressions:
When simplifying algebraic expressions that involve radicals, the square root of half can be used to simplify terms.
Example:
- Simplify \( \sqrt{\frac{4}{8}} \).
- Rewrite as \( \sqrt{\frac{1}{2}} \).
- This simplifies to \( \frac{\sqrt{2}}{2} \).
- Trigonometric Functions:
In trigonometry, the square root of half appears in the values of sine and cosine for common angles.
Example:
- \( \sin(45^\circ) = \cos(45^\circ) = \frac{\sqrt{2}}{2} \).
- These values are derived from the unit circle and right triangle properties.
- Complex Numbers:
The square root of half is useful when working with complex numbers, especially in polar and rectangular form conversions.
Example:
- Convert \( 1 + i \) to polar form.
- Magnitude \( r = \sqrt{1^2 + 1^2} = \sqrt{2} \).
- Angle \( \theta = \tan^{-1}(1/1) = 45^\circ \).
- Polar form: \( \sqrt{2} (\cos 45^\circ + i \sin 45^\circ) = \sqrt{2} \left( \frac{\sqrt{2}}{2} + i \frac{\sqrt{2}}{2} \right) = 1 + i \).
These examples demonstrate the importance of understanding the square root of half in various algebraic contexts, providing a foundation for more advanced mathematical studies.
Properties of Square Roots
Square roots have several fundamental properties that are essential in various mathematical contexts. Understanding these properties can help simplify expressions and solve equations more efficiently. Here are some key properties of square roots:
The Product Property
The square root of a product is equal to the product of the square roots of the factors:
\[
\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}
\]
For example:
\[
\sqrt{12} = \sqrt{4 \cdot 3} = \sqrt{4} \cdot \sqrt{3} = 2 \cdot \sqrt{3} = 2\sqrt{3}
\]
The Quotient Property
The square root of a quotient is equal to the quotient of the square roots of the numerator and denominator:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]
For example:
\[
\sqrt{\frac{16}{4}} = \frac{\sqrt{16}}{\sqrt{4}} = \frac{4}{2} = 2
\]
The Power Property
The square root of a number raised to any power is equal to the number raised to half of that power:
\[
\sqrt{a^n} = a^{\frac{n}{2}}
\]
For example:
\[
\sqrt{25^2} = 25^{\frac{2}{2}} = 25^1 = 25
\]
Rational and Irrational Numbers
- If the digit in the one's place of a number is 2, 3, 7, or 8, then the number cannot be a perfect square, and its square root will be irrational.
- If a number ends with an odd number of zeros, its square root will be irrational.
- The square root of a perfect square is always a rational number.
Even and Odd Properties
- The square root of an even perfect square is always even.
- The square root of an odd perfect square is always odd.
Imaginary Numbers
The square root of a negative number is considered an imaginary value. For instance:
\[
\sqrt{-9}, \quad \sqrt{-12}
\]
Simplifying Square Roots
Square roots can often be simplified by factoring the number into its prime components. For example:
\[
\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}
\]
Example Problems
| Problem | Solution |
|---|---|
| Simplify: \(\sqrt{6} \cdot \sqrt{3}\) | \[ \sqrt{6} \cdot \sqrt{3} = \sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2} \] |
| Simplify: \(\sqrt{35} \div \sqrt{7}\) | \[ \sqrt{35} \div \sqrt{7} = \sqrt{\frac{35}{7}} = \sqrt{5} \] |
Square Root in Decimal Form
Understanding the square root of a fraction such as \( \frac{1}{2} \) in decimal form involves breaking down the steps and computations clearly. Here's a detailed guide:
The square root of \( \frac{1}{2} \) is expressed mathematically as:
\[
\sqrt{\frac{1}{2}}
\]
We can simplify this expression by using the property of square roots, which allows us to separate the numerator and the denominator:
\[
\sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}}
\]
To express this in decimal form, we can rationalize the denominator by multiplying the numerator and the denominator by \( \sqrt{2} \):
\[
\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]
We know that \( \sqrt{2} \) approximately equals 1.4142. Therefore, we can substitute this value in the expression:
\[
\frac{\sqrt{2}}{2} \approx \frac{1.4142}{2} \approx 0.7071
\]
Thus, the square root of \( \frac{1}{2} \) in decimal form is approximately 0.7071.
Here is a step-by-step summary:
- Start with the expression: \( \sqrt{\frac{1}{2}} \).
- Separate the square root over the numerator and denominator: \( \frac{\sqrt{1}}{\sqrt{2}} \).
- Since \( \sqrt{1} = 1 \), simplify to: \( \frac{1}{\sqrt{2}} \).
- Rationalize the denominator: \( \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \).
- Use the approximate value of \( \sqrt{2} \) (1.4142): \( \frac{1.4142}{2} \).
- Calculate the decimal form: \( 0.7071 \).
This method helps to convert the square root of a fraction into a more usable decimal form, which can be particularly useful in various mathematical applications and real-world scenarios.

Rationalizing the Denominator
Rationalizing the denominator is the process of eliminating the square root or other irrational numbers from the denominator of a fraction. This is done to simplify the expression and make it easier to work with. Here are the steps and examples for rationalizing the denominator:
Basic Steps to Rationalize the Denominator
- Identify the denominator that needs to be rationalized.
- Multiply both the numerator and the denominator by the conjugate of the denominator if it is a binomial, or by the radical itself if it is a monomial.
- Simplify the resulting expression by combining like terms and reducing where possible.
Examples
Example 1: Rationalizing a Monomial Denominator
Consider the fraction \(\frac{1}{\sqrt{2}}\).
- Multiply by the conjugate: \(\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\).
- The denominator is now rationalized, and the expression is simplified.
Example 2: Rationalizing a Binomial Denominator
Consider the fraction \(\frac{3}{2 - \sqrt{5}}\).
- Multiply by the conjugate: \(\frac{3}{2 - \sqrt{5}} \times \frac{2 + \sqrt{5}}{2 + \sqrt{5}} = \frac{3(2 + \sqrt{5})}{(2 - \sqrt{5})(2 + \sqrt{5})}\).
- Use the difference of squares: \(\frac{3(2 + \sqrt{5})}{4 - 5} = \frac{3(2 + \sqrt{5})}{-1}\).
- Simplify: \(\frac{3(2 + \sqrt{5})}{-1} = -3(2 + \sqrt{5}) = -6 - 3\sqrt{5}\).
Example 3: Rationalizing a Fraction with a Variable
Consider the fraction \(\frac{\sqrt{x} + \sqrt{y}}{\sqrt{x}}\).
- Multiply by the radical in the denominator: \(\frac{\sqrt{x} + \sqrt{y}}{\sqrt{x}} \times \frac{\sqrt{x}}{\sqrt{x}} = \frac{\sqrt{x}(\sqrt{x} + \sqrt{y})}{x}\).
- Distribute and simplify: \(\frac{x + \sqrt{xy}}{x} = 1 + \frac{\sqrt{xy}}{x}\).
Conclusion
Rationalizing the denominator is a useful technique in algebra to simplify expressions involving radicals. By following the steps outlined above and practicing with various examples, you can master this method and apply it effectively in your mathematical work.
Khám phá lý do tại sao 'x mũ một phần hai' có nghĩa là căn bậc hai qua video này.
Tại sao "x mũ một phần hai" có nghĩa là căn bậc hai?
READ MORE:
Khám phá mối liên hệ giữa căn bậc hai và lũy thừa một phần hai qua video này.
Căn Bậc Hai và Lũy Thừa Một Phần Hai