Topic square root of one half: The square root of one half is a fascinating mathematical concept with broad applications in various fields such as geometry, physics, and engineering. Understanding this fundamental principle can open doors to deeper mathematical insights and practical applications. Discover its calculation methods, historical significance, and real-world uses in this comprehensive guide.
Table of Content
- Square Root of One Half
- Introduction to the Square Root of One Half
- Mathematical Definition
- Calculation Methods
- Simplified Form
- Historical Background
- Applications in Various Fields
- Square Root in Geometry
- Square Root in Physics
- Square Root in Engineering
- Square Root in Computer Science
- Visual Representation
- Graphical Interpretation
- Complex Numbers and Square Roots
- Relation to Other Mathematical Concepts
- Common Mistakes and Misconceptions
- Frequently Asked Questions
- Practice Problems and Solutions
- Further Reading and Resources
- YOUTUBE: Video này giải thích lý do tại sao căn bậc hai của 1/2 lại bằng tất cả những số này, giúp người xem hiểu rõ hơn về khái niệm này.
Square Root of One Half
The square root of one half can be represented and calculated in various forms. Below is a detailed explanation and step-by-step guide on how to simplify and understand this mathematical concept.
Mathematical Representation
The square root of one half is expressed as:
\[ \sqrt{\frac{1}{2}} \]
This can also be written as:
\[ \frac{1}{\sqrt{2}} \]
Steps to Simplify
- Rewrite the expression:
- Rationalize the denominator by multiplying both the numerator and the denominator by \(\sqrt{2}\):
- The simplified form is:
\[ \sqrt{\frac{1}{2}} = \frac{1}{\sqrt{2}} \]
\[ \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \]
\[ \frac{\sqrt{2}}{2} \]
Decimal Representation
The decimal representation of the square root of one half is approximately:
\[ \frac{\sqrt{2}}{2} \approx 0.7071 \]
Properties and Applications
- Understanding square roots is fundamental in geometry, particularly in calculating the side lengths of squares and other polygons.
- The square root function is used in various fields including physics, engineering, and computer science for different types of calculations.
Examples of Square Roots
| Number | Square Root |
|---|---|
| 1/2 | \(\frac{\sqrt{2}}{2} \approx 0.7071\) |
| 4 | 2 |
| 9 | 3 |
Conclusion
The square root of one half is a common mathematical expression that can be simplified to \(\frac{\sqrt{2}}{2}\). This expression is important in various applications across different scientific and engineering disciplines.
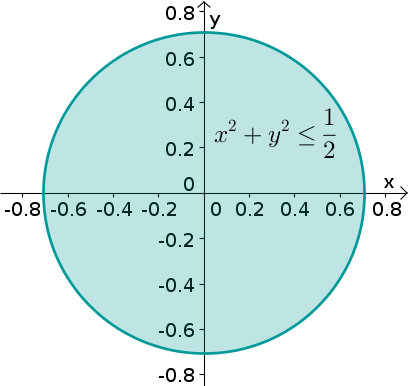
READ MORE:
Introduction to the Square Root of One Half
The square root of one half, represented mathematically as \( \sqrt{\frac{1}{2}} \), is an intriguing concept that arises frequently in various branches of mathematics and its applications. Understanding this concept requires a step-by-step approach to simplify and interpret its value.
Mathematically, the square root of one half can be expressed and simplified as follows:
Let's start with the expression:
\[
\sqrt{\frac{1}{2}}
\]
This can be rewritten using the property of square roots:
\[
\sqrt{\frac{1}{2}} = \sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}}
\]
Simplifying further, we get:
\[
\frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}}
\]
To rationalize the denominator, multiply the numerator and the denominator by \(\sqrt{2}\):
\[
\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]
Thus, the simplified form of \(\sqrt{\frac{1}{2}}\) is \(\frac{\sqrt{2}}{2}\).
The decimal representation of \(\sqrt{\frac{1}{2}}\) is approximately 0.7071, a value that appears in various practical applications, especially in trigonometry and physics.
To further understand the significance and applications of the square root of one half, let's explore some key points:
- Geometry: It is crucial in understanding isosceles right triangles where the legs are of equal length.
- Trigonometry: The value \(\frac{\sqrt{2}}{2}\) corresponds to the sine and cosine of 45 degrees.
- Physics: It appears in wave functions and other physical phenomena.
In conclusion, the square root of one half is not just a numerical value but a fundamental concept with wide-reaching implications in both theoretical and applied mathematics.
Mathematical Definition
The square root of one half, denoted as \( \sqrt{\frac{1}{2}} \), is a fundamental mathematical concept. It represents the value that, when multiplied by itself, yields one half. Let's delve into its mathematical definition and simplification.
Starting with the expression:
\[
\sqrt{\frac{1}{2}}
\]
This can be broken down using the properties of square roots:
\[
\sqrt{\frac{1}{2}} = \sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}}
\]
Given that \(\sqrt{1} = 1\), we have:
\[
\frac{1}{\sqrt{2}}
\]
To simplify further, we rationalize the denominator by multiplying both the numerator and the denominator by \(\sqrt{2}\):
\[
\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]
Thus, the simplified form of \( \sqrt{\frac{1}{2}} \) is:
\[
\frac{\sqrt{2}}{2}
\]
To summarize:
- \(\sqrt{\frac{1}{2}}\) is the value that, when squared, equals \(\frac{1}{2}\).
- The simplified form of \(\sqrt{\frac{1}{2}}\) is \(\frac{\sqrt{2}}{2}\).
- In decimal form, \(\frac{\sqrt{2}}{2}\) is approximately 0.7071.
The value \(\frac{\sqrt{2}}{2}\) is significant in various mathematical contexts, including trigonometry, where it is the sine and cosine of 45 degrees, and in geometry, particularly in the study of isosceles right triangles.
Understanding the mathematical definition and simplification of \(\sqrt{\frac{1}{2}}\) provides a foundation for exploring its applications and significance in broader mathematical and scientific fields.
Calculation Methods
Calculating the square root of one half can be approached in several ways, each providing insight into the value and its properties. Here, we will explore both algebraic and numerical methods for finding \( \sqrt{\frac{1}{2}} \).
Algebraic Method
The algebraic approach involves simplifying the expression using properties of square roots and rationalization.
- Start with the expression:
\[
\sqrt{\frac{1}{2}}
\] - Rewrite the expression as a fraction of square roots:
\[
\sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}}
\] - Simplify \(\sqrt{1}\) to 1:
\[
\frac{1}{\sqrt{2}}
\] - Rationalize the denominator by multiplying both the numerator and the denominator by \(\sqrt{2}\):
\[
\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]
Thus, the simplified form is \(\frac{\sqrt{2}}{2}\).
Numerical Method
Numerical methods involve approximating the value using calculators or computational tools.
- Use a scientific calculator to find:
\[
\sqrt{0.5}
\] - The calculator will yield an approximate value of 0.7071.
This approximation confirms that \(\frac{\sqrt{2}}{2} \approx 0.7071\).
Using Exponents
Another method involves using exponents to express the square root.
- Rewrite the fraction as an exponent:
\[
\left(\frac{1}{2}\right)^{\frac{1}{2}}
\] - Use the property of exponents:
\[
\left(\frac{1}{2}\right)^{\frac{1}{2}} = \frac{1^{\frac{1}{2}}}{2^{\frac{1}{2}}} = \frac{1}{\sqrt{2}}
\] - Rationalize the denominator as shown previously:
\[
\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]
Conclusion
By using these different calculation methods, we can understand and verify the value of \( \sqrt{\frac{1}{2}} \) as \(\frac{\sqrt{2}}{2}\). Whether using algebraic simplification, numerical approximation, or exponent properties, the result remains consistent, demonstrating the robustness of mathematical principles.
Simplified Form
The square root of one half can be simplified into a more familiar form, making it easier to use in mathematical calculations. This involves expressing the value in a way that avoids fractions under the square root. Here, we will take a step-by-step approach to simplify \( \sqrt{\frac{1}{2}} \).
Step-by-Step Simplification
- Start with the initial expression:
\[
\sqrt{\frac{1}{2}}
\] - Apply the property of square roots to separate the numerator and the denominator:
\[
\sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}}
\] - Simplify the square root of the numerator:
\[
\sqrt{1} = 1
\]Thus, the expression becomes:
\[
\frac{1}{\sqrt{2}}
\] - Rationalize the denominator by multiplying both the numerator and the denominator by \(\sqrt{2}\):
\[
\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]
Understanding the Simplified Form
The final simplified form is:
\[
\sqrt{\frac{1}{2}} = \frac{\sqrt{2}}{2}
\]
This form is often more useful in mathematical contexts, particularly in trigonometry and geometry.
- In trigonometry, \(\frac{\sqrt{2}}{2}\) represents the sine and cosine of a 45-degree angle.
- In geometry, it appears in calculations involving isosceles right triangles, where the legs are equal, and the hypotenuse is related to the legs by a factor of \(\sqrt{2}\).
- In physics, it is used in various wave functions and other phenomena where ratios of lengths or amplitudes are important.
Numerical Approximation
In decimal form, \(\frac{\sqrt{2}}{2}\) is approximately:
\[
0.7071
\]
This approximation can be useful for quick calculations or when an exact form is not necessary.
Conclusion
The simplified form of \( \sqrt{\frac{1}{2}} \) as \(\frac{\sqrt{2}}{2}\) provides a clear and practical way to work with this value in various mathematical and scientific applications. By understanding and using this simplified form, one can simplify complex calculations and gain deeper insights into the relationships between different mathematical concepts.

Historical Background
The concept of the square root, including the square root of one half, has a rich historical background rooted in the development of mathematics. The understanding and notation of square roots have evolved significantly over centuries.
Ancient Civilizations
Early mathematical records from ancient civilizations such as the Babylonians and Egyptians show their use of square roots in solving practical problems. The Babylonians, in particular, had methods for approximating square roots around 1900 BC, which were remarkably accurate.
Greek Mathematics
In ancient Greece, mathematicians like Pythagoras and Euclid made significant advancements in geometry and number theory, laying the groundwork for understanding square roots. Euclid's Elements, written around 300 BC, includes geometric methods for finding square roots.
Indian Mathematics
Indian mathematicians, including Aryabhata and Brahmagupta, further developed algorithms for computing square roots. In the 5th century, Aryabhata described a method for extracting square roots in his work Aryabhatiya.
Islamic Golden Age
During the Islamic Golden Age, mathematicians such as Al-Khwarizmi and Al-Kashi refined and expanded upon previous methods for calculating square roots. Al-Khwarizmi's work introduced the algorithmic approach that influenced later European mathematicians.
European Renaissance
In the European Renaissance, the introduction of the printing press facilitated the spread of mathematical knowledge. Mathematicians such as Fibonacci, in his book Liber Abaci (1202), presented methods for finding square roots. The symbol √, used to denote square roots, was introduced by the German mathematician Christoff Rudolff in 1525.
Modern Developments
In modern mathematics, the understanding of square roots has become fundamental, with applications across various fields. The development of calculus and algebra provided tools for deeper exploration and more complex applications of square roots, including the square root of one half.
Conclusion
The historical development of the square root concept demonstrates the cumulative nature of mathematical knowledge. From ancient civilizations to modern times, the ability to compute and understand square roots has been essential for advancements in science, engineering, and mathematics. The square root of one half, while a simple concept today, is a part of this rich historical tapestry.
Applications in Various Fields
The square root of one half, \( \sqrt{\frac{1}{2}} \), or equivalently \( \frac{\sqrt{2}}{2} \), appears in various fields, playing a critical role in many practical and theoretical contexts. Here, we explore its applications in several key areas.
Trigonometry
In trigonometry, the value \( \frac{\sqrt{2}}{2} \) is fundamental. It represents the sine and cosine of a 45-degree angle (or \( \pi/4 \) radians). This can be seen in the unit circle where:
\[
\sin\left(\frac{\pi}{4}\right) = \cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}
\]
These values are essential in solving problems involving right triangles and circular motion.
Geometry
In geometry, \( \frac{\sqrt{2}}{2} \) appears in the study of isosceles right triangles. If the legs of such a triangle are of length 1, the hypotenuse will be:
\[
\sqrt{1^2 + 1^2} = \sqrt{2}
\]
The height and base of the triangle divided by the hypotenuse give:
\[
\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]
This is used to find the lengths of segments and angles in various geometric shapes.
Physics
In physics, \( \frac{\sqrt{2}}{2} \) is frequently encountered in wave mechanics and quantum physics. For instance, it is used in describing the amplitudes of waves where interference patterns occur. Additionally, in quantum mechanics, it appears in the normalization of wave functions.
Engineering
Engineers use \( \frac{\sqrt{2}}{2} \) in signal processing and electrical engineering. In alternating current (AC) circuit analysis, the root mean square (RMS) value of a sinusoidal wave is:
\[
V_{rms} = V_{peak} \times \frac{\sqrt{2}}{2}
\]
This value is critical for calculating power and efficiency in AC circuits.
Computer Science
In computer graphics and digital image processing, \( \frac{\sqrt{2}}{2} \) helps in algorithms for rotation, scaling, and other transformations. For example, rotating a point around the origin by 45 degrees involves multiplying the coordinates by \( \frac{\sqrt{2}}{2} \) in both the x and y directions.
Statistics
In statistics, \( \frac{\sqrt{2}}{2} \) can appear in the calculation of certain probability distributions and their normalizations. It is also used in algorithms for estimating population variances and standard deviations.
Conclusion
The square root of one half is a versatile and widely used value in mathematics and science. Its appearance in trigonometry, geometry, physics, engineering, computer science, and statistics highlights its importance and utility across various disciplines. Understanding this value and its applications can provide deeper insights into both theoretical and practical problems.
Square Root in Geometry
The square root of one half, \( \sqrt{\frac{1}{2}} \), or \( \frac{\sqrt{2}}{2} \), plays a significant role in various geometric contexts. Here, we will explore its applications and importance in geometry, step by step.
Isosceles Right Triangle
An isosceles right triangle has two equal legs and one hypotenuse. If each leg is of length 1, the hypotenuse can be found using the Pythagorean theorem:
\[
\text{Hypotenuse} = \sqrt{1^2 + 1^2} = \sqrt{2}
\]
The length of each leg divided by the hypotenuse is:
\[
\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]
Thus, the sine and cosine of a 45-degree angle in this triangle are both \( \frac{\sqrt{2}}{2} \).
Unit Circle
In the unit circle, which is a circle with radius 1 centered at the origin, the coordinates of points on the circle correspond to trigonometric functions. For a 45-degree angle (or \( \pi/4 \) radians), the coordinates are:
\[
\left( \cos\left(\frac{\pi}{4}\right), \sin\left(\frac{\pi}{4}\right) \right) = \left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)
\]
These coordinates demonstrate the relationship between the unit circle and the square root of one half.
Diagonals of Squares
The diagonal of a square splits it into two isosceles right triangles. If the side length of the square is \( s \), the diagonal length \( d \) can be found using:
\[
d = s\sqrt{2}
\]
For a unit square (side length \( s = 1 \)):
\[
d = 1\sqrt{2} = \sqrt{2}
\]
Thus, the length of the diagonal divided by the side length is \( \sqrt{2} \), which is directly related to the concept of \( \sqrt{\frac{1}{2}} \) when considering the proportionality of the triangle sides.
Similarity and Scaling
In geometric transformations involving similarity and scaling, \( \sqrt{\frac{1}{2}} \) is used to scale figures proportionally. For instance, reducing a figure's dimensions by \( \sqrt{\frac{1}{2}} \) scales down the area by one half while preserving the shape's properties.
Geometric Constructions
In classical geometric constructions using a compass and straightedge, the value \( \frac{\sqrt{2}}{2} \) arises frequently. Constructing a square's diagonal, for example, provides a practical demonstration of this value.
Conclusion
The square root of one half is integral to understanding geometric principles and solving problems related to triangles, circles, squares, and transformations. Its presence in fundamental geometric constructs highlights its importance and utility in mathematics.
Square Root in Physics
The concept of the square root of one half, \( \sqrt{\frac{1}{2}} \), finds applications in various areas of physics. One of the most significant areas is in the calculation of root mean square (RMS) values, which are crucial for understanding alternating current (AC) circuits and signals.
In the context of AC circuits, the RMS value of a quantity (such as voltage or current) is a statistical measure of the magnitude of a varying quantity. It is particularly useful because it provides a measure of the equivalent direct current (DC) value that would produce the same power dissipation in a resistive load.
For a sinusoidal waveform, the RMS value is given by:
\[ V_{RMS} = V_{peak} \times \sqrt{\frac{1}{2}} = V_{peak} \times \frac{1}{\sqrt{2}} \approx V_{peak} \times 0.707 \]
Here, \( V_{RMS} \) is the RMS voltage, and \( V_{peak} \) is the peak voltage of the sine wave. This relationship shows how the square root of one half is directly involved in converting the peak value to the RMS value.
In practical terms, this means that if the peak voltage of an AC signal is 325V, the RMS voltage would be:
\[ 325 \times 0.707 \approx 230V \]
Understanding RMS values is crucial in various fields such as:
- Electrical Engineering: RMS values are used to design and analyze AC circuits, ensuring that electrical systems are both safe and efficient.
- Power Distribution: RMS values help in calculating the power delivered by AC sources, which is essential for the correct sizing of generators, transformers, and other equipment.
- Signal Processing: RMS measurements are used to analyze signal strength and power in telecommunications and audio engineering.
Additionally, the square root of one half appears in the context of quantum mechanics and wave functions, where it can be used in the normalization of wave functions and in the calculation of probabilities.
In summary, the square root of one half, \( \sqrt{\frac{1}{2}} \), plays a vital role in physics, especially in the understanding and application of RMS values in AC circuits, making it a fundamental concept in both theoretical and applied physics.
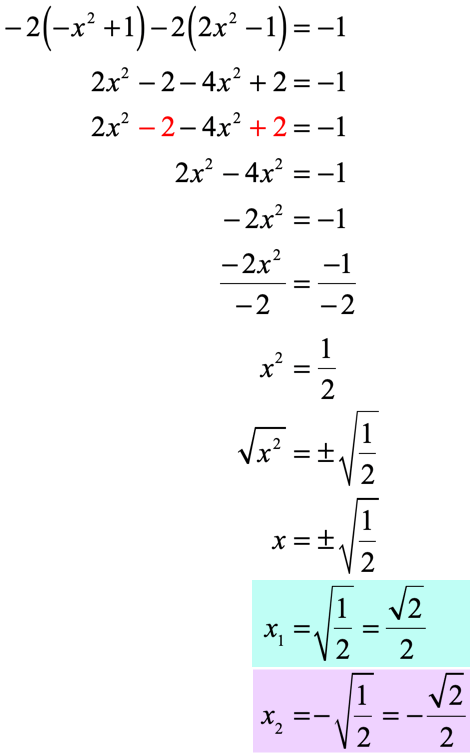
Square Root in Engineering
The square root of one half, often denoted as \( \sqrt{\frac{1}{2}} \) or \( \frac{1}{\sqrt{2}} \), plays a significant role in various engineering applications. Its importance is particularly evident in fields such as civil, electrical, and mechanical engineering.
1. Signal Processing and Communications
In signal processing, the square root of one half is crucial for the normalization of signal power. When dealing with sinusoidal waveforms, the root mean square (RMS) value is used to determine the effective power of an AC signal. For a sinusoidal signal \( V(t) = V_0 \sin(\omega t) \), the RMS value is given by:
\[ V_{\text{RMS}} = V_0 \cdot \sqrt{\frac{1}{2}} \]
This value ensures that the power calculations for AC signals are consistent with those for DC signals, facilitating accurate design and analysis of electrical circuits.
2. Structural Engineering and Load Distribution
In structural engineering, the concept of load distribution often involves the square root of one half. For example, when considering the load transfer in diagonal members of trusses or frameworks, the effective load component along the diagonal is influenced by this factor. If a load \( P \) is applied at a 45-degree angle, the vertical and horizontal components of the load are:
\[ P_x = P \cdot \cos(45^\circ) = P \cdot \sqrt{\frac{1}{2}} \]
\[ P_y = P \cdot \sin(45^\circ) = P \cdot \sqrt{\frac{1}{2}} \]
This ensures that the load is evenly distributed between the two directions, critical for maintaining structural integrity and balance.
3. Soil Mechanics and Consolidation Testing
In geotechnical engineering, the square root of one half is used in the analysis of soil consolidation tests, such as the Oedometer test. The Taylor Square Root of Time Fitting Method uses the square root of time to determine the coefficient of consolidation \( C_v \). This method involves plotting the deformation of the soil sample against the square root of time to estimate the rate at which soil consolidation occurs:
\[ C_v = 0.848 \cdot \left(\frac{H_{dr}^2}{t_{90}}\right) \]
where \( H_{dr} \) is the drainage path and \( t_{90} \) is the time for 90% consolidation. This calculation is essential for predicting settlement and ensuring the stability of foundations.
4. Electrical Engineering and RMS Values
The square root of one half is also vital in electrical engineering when calculating RMS values for alternating current (AC) signals. RMS values are used to represent the equivalent DC value of an AC signal, which is essential for power calculations and thermal management in electronic components:
\[ V_{\text{RMS}} = V_{\text{peak}} \cdot \sqrt{\frac{1}{2}} \]
This calculation allows engineers to design circuits and systems that can efficiently handle AC power without overheating or inefficiencies.
The ubiquitous presence of \( \sqrt{\frac{1}{2}} \) across various engineering disciplines underscores its importance in practical applications, enabling precise calculations and optimized designs.
Square Root in Computer Science
The concept of square roots, particularly the square root of one half, is fundamental in various computational algorithms and applications. One notable example is the fast inverse square root algorithm, famously used in computer graphics.
This algorithm, known for its use in the game Quake III Arena, computes an approximation of \( \frac{1}{\sqrt{x}} \) efficiently. Here’s a simplified version of the algorithm:
float Q_rsqrt(float number) {
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y;
i = 0x5f3759df - ( i >> 1 );
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) );
return y;
}
This function rapidly approximates the inverse square root of a number by leveraging bit manipulation techniques. It was designed to optimize performance in 3D graphics by normalizing vectors, which involves dividing each vector component by its magnitude:
{\displaystyle \|{\boldsymbol {v}}\|={\sqrt {v_{1}^{2}+v_{2}^{2}+v_{3}^{2}}}}
Here, \( \boldsymbol{v} \) is a vector, and \( \|{\boldsymbol{v}}\| \) is its Euclidean norm. The algorithm calculates this efficiently, reducing the computational load in real-time rendering tasks.
Such techniques are essential in computer science, especially in fields requiring high-performance calculations like gaming, simulations, and real-time systems. Understanding and implementing efficient mathematical algorithms can significantly enhance the performance and accuracy of computational applications.
Visual Representation
The visual representation of the square root of one half (√1/2) can be understood through several graphical and geometric interpretations. Visual models help in comprehending the concept by transforming abstract mathematical expressions into tangible forms.
Square Root Representation on Number Line
One of the simplest ways to represent √1/2 is on a number line. By plotting the point corresponding to 0.707 (since √1/2 ≈ 0.707), we can visualize its approximate position between 0 and 1.

Geometric Interpretation
The geometric interpretation involves creating a right triangle where the length of one leg is 1, and the length of the hypotenuse is √2. The length of the other leg, being √1/2, can be visualized as follows:
- Draw a right triangle with legs of lengths 1 and √1/2.
- The hypotenuse of this triangle will be 1.
- This helps in understanding that the length √1/2 is effectively the geometric mean of 1 and √2.

Graphical Interpretation Using Desmos
Graphing tools like Desmos can be used to create a visual representation of √1/2. By plotting the function y = √(1/2), you can observe its behavior and see how it fits into the larger context of square root functions.
Square Root Charts
Square root charts provide a tabular form of various square roots, including √1/2. These charts often include visual aids that show how the square root relates to the areas of squares.

Visual Models and Manipulatives
Using visual models like cut paper squares can approximate the square root of non-perfect squares. This method, although approximate, provides an intuitive grasp of the concept.
- Start with a square of area 1.
- Divide it into two equal smaller squares, each with an area of 1/2.
- The side length of each smaller square represents √1/2.

This hands-on approach makes the abstract notion of square roots more concrete and accessible, especially for educational purposes.
Graphical Interpretation
The square root of one half, represented as \( \sqrt{\frac{1}{2}} \), can be visualized in various ways. Here, we will explore its graphical interpretation using Cartesian coordinates and transformations.
Basic Graph of the Square Root Function
The square root function \( f(x) = \sqrt{x} \) is a common function in mathematics. Its graph is a curve that starts at the origin (0,0) and increases gradually. It is defined only for non-negative values of x.
To understand \( \sqrt{\frac{1}{2}} \), let's first recall the graph of \( y = \sqrt{x} \):
- The domain is \( [0, \infty) \).
- The range is \( [0, \infty) \).
- The function is increasing for all \( x \geq 0 \).
Plotting \( \sqrt{\frac{1}{2}} \) on the Graph
Consider the function \( y = \sqrt{\frac{1}{2}} \). On the graph of \( y = \sqrt{x} \), locate the point where \( x = \frac{1}{2} \). The y-coordinate at this point will be \( \sqrt{\frac{1}{2}} \approx 0.707 \).
The process involves:
- Finding the point \( x = \frac{1}{2} \) on the x-axis.
- Moving vertically to the point on the curve \( y = \sqrt{x} \).
- Reading the corresponding y-value, which is \( \sqrt{\frac{1}{2}} \).
This point can be plotted as \(( \frac{1}{2}, \sqrt{\frac{1}{2}} )\).
Graphing Square Root Transformations
Graphing the function \( y = \sqrt{\frac{1}{2}} x \) involves transformations of the parent function \( y = \sqrt{x} \). This specific transformation scales the function horizontally.
Using Desmos or another graphing tool, you can input the function and observe the changes. The transformation results in a horizontal compression of the graph.
Example Graph
Below is a table of values for the function \( y = \sqrt{\frac{1}{2} x} \) to help with graphing:
| x | y |
|---|---|
| 0 | 0 |
| 0.5 | 0.5 |
| 1 | 0.707 |
| 2 | 1 |
Plot these points and join them to form a curve. This graph helps visualize how the square root function behaves when scaled by \( \frac{1}{2} \).
Conclusion
Graphical interpretations of mathematical functions like \( \sqrt{\frac{1}{2}} \) offer intuitive insights into their behavior and transformations. Using tools like Desmos enhances our understanding through visual learning.
Complex Numbers and Square Roots
Understanding the square root of one half in the context of complex numbers requires a grasp of both real and imaginary components of numbers. In the complex plane, numbers are represented as a + bi, where a and b are real numbers, and i is the imaginary unit, defined by i² = -1.
Let's denote the square root of one half as √(1/2). We can write this as 1/√2, which is equivalent to √2/2 in its simplified form. For complex numbers, we can express the square root operation involving real and imaginary parts as follows:
Consider a complex number z = a + bi. The square roots of z are the solutions to the equation (x + yi)² = a + bi. This expands and equates to two separate equations:
- x² - y² = a
- 2xy = b
For the square root of one half, where a = 1/2 and b = 0, the equations simplify to:
- x² - y² = 1/2
- 2xy = 0
Given 2xy = 0, either x or y must be zero. This leads to two possible scenarios:
- If y = 0, then x² = 1/2, giving x = ±√(1/2) = ±1/√2 = ±√2/2.
- If x = 0, then y² = -1/2, which is not possible for real y.
Thus, the square roots of one half in the complex plane are ±√2/2 and have no imaginary component.
We can also explore this geometrically in the complex plane. The modulus of a complex number z = a + bi is given by |z| = √(a² + b²). For z = √(1/2), the modulus is:
|z| = √((√2/2)²) = √(1/2) = 1/√2
In polar form, a complex number is expressed as reiθ. For r = 1/√2 and θ = 0 (since the imaginary part is zero), the square root remains 1/√2.
To summarize:
- The square roots of one half in the complex number system are ±√2/2.
- The imaginary component does not affect the square root of a real positive fraction like one half.
- Geometrically, these roots lie on the real axis in the complex plane.
Relation to Other Mathematical Concepts
The square root of one half, represented as \( \sqrt{\frac{1}{2}} \), is intricately related to various mathematical concepts. Understanding these relationships can provide deeper insights into the properties and applications of square roots.
Exponents and Radicals
One fundamental relationship is between square roots and exponents. The square root of a number can be expressed using fractional exponents:
\[
\sqrt{x} = x^{\frac{1}{2}}
\]
Therefore,
\[
\sqrt{\frac{1}{2}} = \left( \frac{1}{2} \right)^{\frac{1}{2}}
\]
Trigonometry
In trigonometry, the value of \( \sqrt{\frac{1}{2}} \) appears frequently, particularly in the context of sine and cosine functions for common angles. For example:
\[
\sin(45^\circ) = \cos(45^\circ) = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]
Complex Numbers
The concept of square roots extends into the realm of complex numbers. The square root of a negative number involves imaginary units:
\[
\sqrt{-1} = i
\]
Thus,
\[
\sqrt{-\frac{1}{2}} = \sqrt{-1 \cdot \frac{1}{2}} = i \sqrt{\frac{1}{2}} = \frac{i}{\sqrt{2}}
\]
Irrational Numbers
Numbers like \( \sqrt{\frac{1}{2}} \) are irrational, meaning they cannot be expressed as a simple fraction. This property places them within the broader category of irrational numbers, which include roots of non-perfect squares.
Geometric Interpretation
Geometrically, the square root function describes the side length of a square with a given area. For \( \sqrt{\frac{1}{2}} \), it represents the side length of a square with half a unit area.
Applications in Physics and Engineering
In physics, the square root function appears in formulas involving kinetic energy, wave functions, and more. For example, the normalization factor in quantum mechanics often involves square roots. In engineering, square roots are used in signal processing and control theory.
Understanding these relationships enhances comprehension of the square root function and its extensive applications across different fields of mathematics and science.
Common Mistakes and Misconceptions
Understanding the square root of one half, \(\sqrt{\frac{1}{2}}\), involves avoiding several common mistakes and misconceptions that often arise in mathematics. Here are some of the key points to consider:
-
Misunderstanding the Square Root Definition:
One common mistake is assuming that \(\sqrt{\frac{1}{2}} = \frac{1}{2}\). In fact, \(\sqrt{\frac{1}{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\) after rationalizing the denominator.
-
Ignoring Both Positive and Negative Roots:
When solving equations involving square roots, it is crucial to remember that \(\sqrt{x^2} = |x|\). Thus, for \(\sqrt{\frac{1}{2}}\), both positive and negative values should be considered: \(\pm\frac{\sqrt{2}}{2}\).
-
Incorrect Simplification:
Another mistake is improperly simplifying expressions. For instance, mistakenly simplifying \(\sqrt{\frac{1}{2}}\) directly to \(\frac{1}{2}\) without rationalizing the denominator or verifying the correct form.
-
Errors with Radicals:
Students sometimes assume incorrect properties of radicals, such as \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\), which is not generally true. Correct handling of radicals requires careful application of properties: \(\sqrt{\frac{1}{2}} = \sqrt{1 \cdot \frac{1}{2}} = \sqrt{1} \cdot \sqrt{\frac{1}{2}}\).
-
Overlooking Rationalization:
Failing to rationalize the denominator is a common error. The expression \(\frac{1}{\sqrt{2}}\) should be rationalized to \(\frac{\sqrt{2}}{2}\) by multiplying the numerator and the denominator by \(\sqrt{2}\).
-
Forgetting Complex Numbers:
When dealing with square roots in the context of complex numbers, it is essential to remember that \(\sqrt{-1} = i\), where \(i\) is the imaginary unit. This can affect the interpretation and solution of equations involving square roots.
To master these concepts, it is important to practice and understand the properties of square roots, radicals, and complex numbers thoroughly.
Frequently Asked Questions
Here are some common questions related to the square root of one half:
- What is the square root of 1/2?
The square root of \( \frac{1}{2} \) is \( \frac{\sqrt{2}}{2} \). This is derived by recognizing that \( \sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} \), which simplifies to \( \frac{1}{\sqrt{2}} \). By rationalizing the denominator, multiplying by \( \frac{\sqrt{2}}{\sqrt{2}} \), we get \( \frac{\sqrt{2}}{2} \).
- How do you simplify the square root of 1/2?
To simplify \( \sqrt{\frac{1}{2}} \):
- Write the square root as a fraction: \( \sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} \).
- Simplify the numerator: \( \frac{1}{\sqrt{2}} \).
- Rationalize the denominator by multiplying by \( \frac{\sqrt{2}}{\sqrt{2}} \): \( \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2} \).
- Can the square root of 1/2 be expressed in decimal form?
Yes, the square root of 1/2 can be expressed in decimal form as approximately 0.7071. This is because \( \frac{\sqrt{2}}{2} \approx \frac{1.4142}{2} \approx 0.7071 \).
- Why is it important to rationalize the denominator?
Rationalizing the denominator is important because it avoids having a radical in the denominator, which is generally considered a less simplified form. It also often makes the number easier to interpret and use in further calculations.
- Are there any practical applications for the square root of 1/2?
Yes, the square root of 1/2 appears in various fields such as geometry (e.g., in the computation of angles in right triangles), physics (e.g., in wave equations), and engineering (e.g., in signal processing). It is a common value in trigonometric functions as well.

Practice Problems and Solutions
Below are some practice problems involving the square root of one half, along with detailed solutions to help reinforce your understanding.
-
Find the square root of \( \frac{1}{2} \).
Solution:
We know that \( \sqrt{\frac{1}{2}} = \frac{1}{\sqrt{2}} \). To rationalize the denominator, we multiply by \( \frac{\sqrt{2}}{\sqrt{2}} \):
\[
\sqrt{\frac{1}{2}} = \frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\] -
Simplify the expression \( \sqrt{\frac{4}{8}} \).
Solution:
Simplify the fraction inside the square root first:
\[
\sqrt{\frac{4}{8}} = \sqrt{\frac{1}{2}} = \frac{\sqrt{2}}{2}
\] -
Find the value of \( \sqrt{2} \times \sqrt{\frac{1}{2}} \).
Solution:
Use the property of square roots that \( \sqrt{a} \times \sqrt{b} = \sqrt{a \times b} \):
\[
\sqrt{2} \times \sqrt{\frac{1}{2}} = \sqrt{2 \times \frac{1}{2}} = \sqrt{1} = 1
\] -
Solve for \( x \) in the equation \( x^2 = \frac{1}{2} \).
Solution:
Take the square root of both sides:
\[
x = \pm \sqrt{\frac{1}{2}} = \pm \frac{\sqrt{2}}{2}
\] -
If \( \frac{1}{2} = x \cdot x \), find the value of \( x \).
Solution:
This is similar to the previous problem. Taking the square root of both sides gives:
\[
x = \pm \sqrt{\frac{1}{2}} = \pm \frac{\sqrt{2}}{2}
\] -
Simplify \( \frac{1}{\sqrt{2}} \times \sqrt{2} \).
Solution:
Multiply the fractions directly:
\[
\frac{1}{\sqrt{2}} \times \sqrt{2} = \frac{\sqrt{2}}{\sqrt{2}} = 1
\] -
Evaluate \( \left(\sqrt{\frac{1}{2}}\right)^2 \).
Solution:
Square the expression:
\[
\left(\sqrt{\frac{1}{2}}\right)^2 = \frac{1}{2}
\]
These problems and solutions should help reinforce your understanding of the square root of one half and related concepts.
Further Reading and Resources
To gain a deeper understanding of the square root of one half and related mathematical concepts, here are some recommended resources and readings:
-
Khan Academy:
Explore various topics on square roots, including simplifying square roots, the properties of square roots, and applications in algebra.
Visit:
-
Math is Fun:
This site provides clear explanations and examples of square roots and their properties, making it accessible for learners at different levels.
Visit:
-
Wolfram Alpha:
Use Wolfram Alpha for computational exploration and to verify calculations involving the square root of one half. It offers detailed step-by-step solutions.
Visit:
-
Coursera - Pre-Calculus:
This course covers fundamental mathematical concepts, including square roots, and is suitable for high school students and those preparing for calculus.
Visit:
-
Books and Publications:
-
The Joy of x: A Guided Tour of Math, from One to Infinity by Steven Strogatz - This book offers an engaging exploration of mathematical concepts, including roots and their applications.
-
Principles of Mathematics by Carl Barnett Smith - A comprehensive textbook covering various mathematical principles, including the manipulation and application of square roots.
-
By exploring these resources, you can enhance your understanding of the square root of one half and its significance in various mathematical contexts.
READ MORE:
Video này giải thích lý do tại sao căn bậc hai của 1/2 lại bằng tất cả những số này, giúp người xem hiểu rõ hơn về khái niệm này.
Căn bậc hai của 1/2 bằng TẤT CẢ những số này! #shorts














