Topic 1 2 square root of 3 triangle: Discover the fascinating properties of the 1 2 square root of 3 triangle, a special right triangle with unique characteristics and applications in geometry. Learn about its side ratios, angle measures, and how to solve for its sides using simple formulas and trigonometric principles.
Table of Content
- 1 2 Square Root of 3 Triangle
- Introduction
- Understanding the 1-2-√3 Triangle
- Mathematical Properties
- Derivation and Proof
- Applications in Geometry
- Comparative Analysis
- Visualization and Diagrams
- Practical Examples
- Conclusion
- YOUTUBE: Video giới thiệu về tam giác một hai căn bậc ba, giải thích các tính chất và ứng dụng trong hình học. Phù hợp cho những ai muốn tìm hiểu về tam giác đặc biệt này.
1 2 Square Root of 3 Triangle
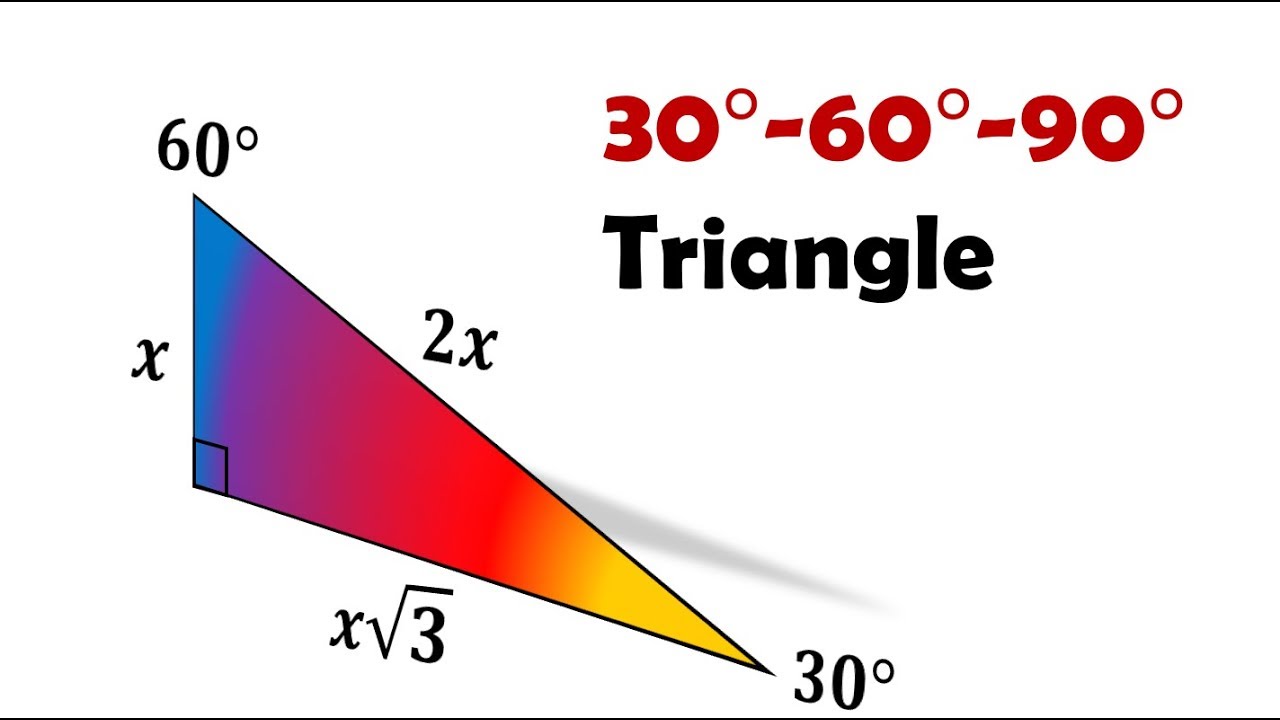
The 30-60-90 triangle is a special type of right triangle, known for its unique ratio of the lengths of its sides, which are in the proportion 1:√3:2. This makes it a frequently discussed topic in trigonometry and geometry.
Properties of a 30-60-90 Triangle
- Angles: 30°, 60°, and 90°
- Side Ratios: 1:√3:2
- Formed by splitting an equilateral triangle in half
Trigonometric Ratios
The sides of a 30-60-90 triangle provide simple trigonometric ratios:
| Angle | Sin | Cos | Tan |
|---|---|---|---|
| 30° | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{3}}\) |
| 60° | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | \(\sqrt{3}\) |
Formulas
Given a 30-60-90 triangle with the shortest side (opposite the 30° angle) of length \(a\):
- Length of the side opposite the 60° angle: \(a\sqrt{3}\)
- Length of the hypotenuse: \(2a\)
Applications and Examples
The 30-60-90 triangle is used to simplify many geometric problems. Here are some examples:
- Example 1: If the shortest side is 5 units, the other sides are 5√3 and 10 units.
- Example 2: In a triangle with sides 4, 4√3, and 8 units, verify if it's a 30-60-90 triangle by checking the ratio 1:√3:2.
The 30-60-90 triangle's properties and simplicity in side ratios make it a fundamental topic in trigonometry and geometry studies.
READ MORE:
Introduction
The 30-60-90 triangle is a special type of right triangle characterized by its unique angle measures and side length ratios. This triangle is distinguished by its angles, which are 30°, 60°, and 90°, and its side lengths, which follow the ratio 1:√3:2. Understanding the properties of the 30-60-90 triangle is crucial for solving various geometric problems efficiently.
In a 30-60-90 triangle:
- The side opposite the 30° angle is the shortest and is designated as \(a\).
- The side opposite the 60° angle, known as the longer leg, is \(a\sqrt{3}\).
- The hypotenuse, which is opposite the 90° angle, is \(2a\).
These relationships are derived from the properties of equilateral triangles, as a 30-60-90 triangle can be formed by dividing an equilateral triangle in half. This type of triangle has practical applications in trigonometry, allowing for quick calculations of side lengths and angles. Moreover, it serves as a fundamental concept in many geometry problems, making it essential knowledge for students and professionals alike.
Understanding the 1-2-√3 Triangle
The 1-2-√3 triangle, also known as the 30-60-90 triangle, is a special type of right triangle. It is characterized by its angle measures of 30 degrees, 60 degrees, and 90 degrees, and the unique ratio of its side lengths.
In a 1-2-√3 triangle:
- The shortest side, opposite the 30-degree angle, is of length \(1\).
- The side opposite the 60-degree angle is of length \(\sqrt{3}\).
- The hypotenuse, opposite the 90-degree angle, is of length \(2\).
This specific ratio of side lengths is extremely useful in solving problems involving right triangles without needing to use trigonometric functions directly. The properties of this triangle can be derived and verified using the Pythagorean theorem.
For example, if the shortest side \( x = 1 \), the longer leg will be \( x\sqrt{3} = \sqrt{3} \), and the hypotenuse will be \( 2x = 2 \). Conversely, if the hypotenuse is given as \(2\), the other sides can be calculated by dividing by 2 and multiplying by \(\sqrt{3}\), respectively.
| Angle | Side Opposite |
| 30 degrees | \(1\) |
| 60 degrees | \(\sqrt{3}\) |
| 90 degrees | \(2\) |
Understanding these relationships can simplify many geometric problems and proofs. This triangle frequently appears in various fields, including geometry, trigonometry, and even real-world applications like construction and design.
Mathematical Properties
The 1-2-√3 triangle, also known as the 30-60-90 triangle, is a special type of right triangle with unique properties that make it fundamental in trigonometry and geometry. Here are some key mathematical properties:
- The angles of the triangle are 30°, 60°, and 90°.
- The sides are in the ratio 1 : √3 : 2, corresponding to the opposite side of the 30° angle, the opposite side of the 60° angle, and the hypotenuse, respectively.
- If the length of the shorter leg (opposite the 30° angle) is denoted as \(a\), then:
- The length of the longer leg (opposite the 60° angle) is \(a\sqrt{3}\).
- The length of the hypotenuse is \(2a\).
- The area of the triangle can be calculated as \( \frac{a^2 \sqrt{3}}{2} \).
- The perimeter of the triangle is \( a(3 + \sqrt{3}) \).
- These properties can be derived using basic trigonometric functions and the Pythagorean theorem:
- Using the sine and cosine functions:
- \( \sin(30°) = \frac{1}{2} \) implies \( c = 2a \).
- \( \sin(60°) = \frac{\sqrt{3}}{2} \) implies \( b = a\sqrt{3} \).
- The Pythagorean theorem confirms the relationship: \( a^2 + (a\sqrt{3})^2 = (2a)^2 \).
- Using the sine and cosine functions:
Understanding these properties is essential for solving various problems in trigonometry and geometry, as the 30-60-90 triangle often appears in different mathematical contexts.
Derivation and Proof
The 1-2-√3 triangle, also known as the 30-60-90 triangle, is a special right triangle with unique properties. It is derived from an equilateral triangle, which is divided into two equal 30-60-90 triangles. Here's a step-by-step derivation and proof:
- Start with an equilateral triangle where all sides are equal and each angle measures 60 degrees.
- Draw an altitude from one vertex to the midpoint of the opposite side. This altitude bisects the angle and the opposite side, creating two 30-60-90 triangles.
- Label the sides: if the original side length of the equilateral triangle is \(2a\), the altitude (height) will be \(a\sqrt{3}\) using the Pythagorean theorem.
- Thus, the sides of the 30-60-90 triangle are in the ratio \(1:a:a\sqrt{3}\), corresponding to the side lengths 1, \(\sqrt{3}\), and 2.
The properties of the 1-2-√3 triangle can also be proved using trigonometry:
- In a 30-60-90 triangle, the shortest side (opposite the 30° angle) is half the hypotenuse, or \(1/2\) of the hypotenuse.
- The longer leg (opposite the 60° angle) is \(\sqrt{3}/2\) times the hypotenuse.
- These relationships can be derived using the sine and cosine functions: \[ \sin(30°) = \frac{1}{2} \quad \text{and} \quad \cos(30°) = \frac{\sqrt{3}}{2} \]
Overall, the derivation and proof of the 1-2-√3 triangle demonstrate its fundamental geometric and trigonometric properties, making it a valuable tool in various mathematical applications.

Applications in Geometry
The 1-2-√3 triangle, also known as the 30-60-90 triangle, holds significant applications in various geometric contexts due to its unique properties. This triangle is characterized by its side lengths, which are in the ratio 1:2:√3. Here are some key applications:
- Trigonometry: The 30-60-90 triangle is fundamental in trigonometry. The ratios of its sides are used to define the sine, cosine, and tangent of 30° and 60° angles. For instance, sin(30°) = 1/2, cos(30°) = √3/2, and tan(30°) = 1/√3.
- Architecture: This triangle's properties are utilized in architectural design, particularly in roof slopes and structural angles, ensuring stability and aesthetic appeal.
- Navigation: In navigation, the principles of the 30-60-90 triangle assist in calculating distances and plotting courses, leveraging its predictable angle ratios.
- Engineering: Engineers apply this triangle in designing various components and systems, where precise angle measurements and ratios are critical for functionality.
- Physics: The 1-2-√3 triangle aids in resolving vector components in physics, allowing for the decomposition of forces and motion into orthogonal directions.
- Art and Design: Artists and designers use the 30-60-90 triangle to achieve accurate proportions and perspectives, enhancing the visual harmony of their works.
Understanding the applications of the 1-2-√3 triangle provides a deeper appreciation of its relevance across multiple disciplines, demonstrating the intersection of mathematics with real-world problems.
Comparative Analysis
The 1-2-√3 triangle, often referred to as the 30-60-90 triangle, has unique properties that distinguish it from other right triangles. This section will explore a comparative analysis of the 1-2-√3 triangle in relation to other notable triangles in geometry.
-
Comparison with the 3-4-5 Triangle
The 3-4-5 triangle is a classic example of a right triangle with integer side lengths, known as a Pythagorean triple. In contrast, the 1-2-√3 triangle involves an irrational number (√3), giving it different geometric properties and applications.
-
Angle Measures
While the 3-4-5 triangle has angles that do not have simple trigonometric values, the 1-2-√3 triangle has angles of 30°, 60°, and 90°, making it easier to use in trigonometric calculations and proofs.
-
Application in Trigonometry
The 1-2-√3 triangle is frequently used to derive exact values for the sine, cosine, and tangent of 30° and 60°. This contrasts with the 3-4-5 triangle, which is often used to demonstrate the Pythagorean theorem and integer-based relationships.
-
Geometric Transformations
In geometric transformations, the 1-2-√3 triangle is used in similarity and scaling problems due to its proportional sides. The 3-4-5 triangle, however, is commonly used in problems involving right-angle constructions and grid-based geometry.
-
Historical Context
The 1-2-√3 triangle's historical significance is tied to ancient Greek mathematics and their study of special right triangles. The 3-4-5 triangle dates back even further, with evidence of its use in Babylonian mathematics.
-
Real-World Applications
The 1-2-√3 triangle is essential in engineering and architecture, particularly in designing objects and structures that require specific angle measures. The 3-4-5 triangle is used in construction for ensuring right angles and in various forms of structural analysis.
Visualization and Diagrams
Understanding the 1-2-√3 triangle can be greatly enhanced through visual aids and diagrams. Below, we provide a comprehensive visual representation of this special right triangle, along with detailed explanations to aid in understanding.
Basic Diagram of the 1-2-√3 Triangle
The 1-2-√3 triangle is a special right triangle where the lengths of the sides are in the ratio 1:√3:2. This triangle can be visualized as follows:
- The side opposite the 30° angle (smallest angle) is of length 1.
- The side opposite the 60° angle (medium angle) is of length √3.
- The hypotenuse opposite the right angle (90°) is of length 2.
Below is a simple diagram:
\[
\begin{array}{ccc}
& | & \\
& | & \sqrt{3} \\
& | & \\
1 & | & \\
\angle 30^\circ & \angle 60^\circ & 2 \\
\end{array}
\]
Step-by-Step Construction
To construct a 1-2-√3 triangle, follow these steps:
- Draw a horizontal line segment and label its length as 1.
- At one end of this line segment, construct a vertical line perpendicular to the segment.
- From the endpoint of the horizontal segment, draw a line segment of length 2 making a 60° angle with the horizontal segment. This will be the hypotenuse.
- Drop a perpendicular from the endpoint of the hypotenuse to the horizontal line segment, dividing the hypotenuse into two parts: a vertical segment of length √3 and a horizontal segment of length 1.
Here is a diagram illustrating these steps:
\[
\begin{array}{ccc}
& | & \\
& | & \sqrt{3} \\
& | & \\
1 & \_\_\_ & \sqrt{3} \\
\angle 30^\circ & \_\_\_\_\_\_\_\_\_ & \angle 60^\circ \\
1 & & 2 \\
\end{array}
\]
Interactive Visualization Tools
For interactive diagrams and further exploration, tools such as GeoGebra provide excellent resources. You can use these tools to dynamically change the angles and sides of the triangle to see how the 1-2-√3 relationship is maintained.
Explore more at .
Mathematical Representation with MathJax
Using MathJax, we can represent the sides and angles of the triangle mathematically:
\[
\text{Let } \triangle ABC \text{ be a triangle with } \angle C = 90^\circ, \angle A = 30^\circ, \text{ and } \angle B = 60^\circ.
\]
\[
\text{If } BC = 1, \text{ then } AB = 2 \text{ and } AC = \sqrt{3}.
\]
Real-World Examples
The 1-2-√3 triangle appears in various real-world scenarios such as engineering, architecture, and physics problems. These applications often involve calculating distances, angles, and optimizing structural designs.
Conclusion
Visual aids and interactive tools are invaluable in comprehending the 1-2-√3 triangle's properties. Through diagrams, step-by-step construction, and dynamic visualization tools, learners can gain a deeper understanding of this fundamental geometric shape.
Practical Examples
Here are several practical examples that illustrate the importance and utility of the 1-2-√3 triangle in real-world applications:
Example 1: Calculating Heights
Imagine you need to determine the height of a tree. By standing a certain distance away from the tree and measuring the angle of elevation to the top of the tree, you can use the properties of the 1-2-√3 triangle to find the height.
- Measure the distance from your standing point to the base of the tree (let's say 10 meters).
- Measure the angle of elevation to the top of the tree (let's assume it's 30°).
- Using the 1-2-√3 triangle properties, the height (opposite the 30° angle) is the distance multiplied by √3.
- Height = 10 * √3 meters.
Example 2: Architecture
The 1-2-√3 triangle is often used in architectural design to ensure aesthetic proportions and structural integrity. For instance, when designing a gable roof:
- The slope of the roof can be designed using a 30° angle to achieve a specific pitch.
- If the horizontal distance from the peak to the edge of the roof is known, the height can be calculated using the 1-2-√3 ratios.
Example 3: Trigonometric Ratios
Understanding trigonometric ratios in a 1-2-√3 triangle helps solve various problems involving angles and distances:
- Sine of 30°: sin(30°) = 1/2
- Cosine of 30°: cos(30°) = √3/2
- Tangent of 30°: tan(30°) = 1/√3
- Sine of 60°: sin(60°) = √3/2
- Cosine of 60°: cos(60°) = 1/2
- Tangent of 60°: tan(60°) = √3
Example 4: Navigation
Pilots and navigators use the 1-2-√3 triangle to calculate courses and distances. For example, when determining the shortest path between two points:
- Assume the starting point, destination, and a waypoint form a 1-2-√3 triangle.
- The properties of the triangle help in calculating the distance to the waypoint and the subsequent path to the destination.
Example 5: Computer Graphics
In computer graphics, the 1-2-√3 triangle is used to render 3D models accurately. For example:
- When constructing triangular meshes for 3D objects, using the 1-2-√3 triangle ensures correct proportions and angles.
- Algorithms that involve rotation and scaling can also benefit from the predictable ratios of this special triangle.
These examples demonstrate the versatility and practicality of the 1-2-√3 triangle, making it a valuable tool in various fields such as mathematics, engineering, architecture, and navigation.

Conclusion
The 1-2-√3 triangle, known for its unique properties and ratios, is a fundamental concept in geometry. It serves as a cornerstone for understanding special right triangles, with applications extending to various mathematical problems and real-world scenarios.
Key points to remember about the 1-2-√3 triangle include:
- The side lengths are in the ratio 1 : √3 : 2, corresponding to the angles 30°, 60°, and 90°.
- This triangle is a subset of the 30-60-90 triangle, making it a versatile tool in trigonometry and geometry.
- Understanding this triangle enhances the ability to solve complex geometric problems by simplifying calculations and providing clear relationships between angles and sides.
In summary, mastering the 1-2-√3 triangle's properties not only aids in academic pursuits but also has practical implications in fields such as architecture, engineering, and various STEM applications. Its consistent ratios and ease of use make it an indispensable part of mathematical education.
Video giới thiệu về tam giác một hai căn bậc ba, giải thích các tính chất và ứng dụng trong hình học. Phù hợp cho những ai muốn tìm hiểu về tam giác đặc biệt này.
Một Hai Căn Bậc Ba Tam Giác
READ MORE:
Video hướng dẫn cách tính độ dài cạnh thiếu của một tam giác, giải thích các phương pháp và công thức toán học. Phù hợp cho những ai muốn tìm hiểu về cách tính cạnh của tam giác đặc biệt này.
Cách Tính Độ Dài Cạnh Thiếu Của Một Tam Giác