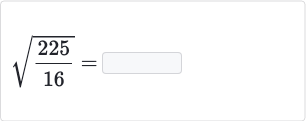
Topic is the square root of 16 rational or irrational: The square root of 16 is a commonly discussed topic in mathematics. In this article, we will explore whether it is rational or irrational, delving into definitions, calculations, and practical applications. Join us as we uncover the nature of this intriguing mathematical concept.
Table of Content
- Understanding the Rationality of the Square Root of 16
- Introduction
- Definition of Rational and Irrational Numbers
- Why the Square Root of 16 is Rational
- Perfect Squares and Their Properties
- Methods to Calculate the Square Root of 16
- Long Division Method
- Calculator and Computer Methods
- Exponent Form
- Simplification of Square Root of 16
- Applications of Square Roots
- YOUTUBE: Tìm hiểu về số hữu tỉ và vô tỉ qua video này. Khám phá các khái niệm và ví dụ cụ thể để hiểu rõ hơn về toán học.
Understanding the Rationality of the Square Root of 16
To determine whether the square root of 16 is rational or irrational, we need to understand the definitions of rational and irrational numbers.
Definitions
- Rational Numbers: These are numbers that can be expressed as the ratio of two integers, where the denominator is not zero. Examples include fractions, integers, and terminating or repeating decimals.
- Irrational Numbers: These numbers cannot be written as a simple fraction. Their decimal expansions are non-terminating and non-repeating. Examples include √2, π, and e.
Square Root of 16
The square root of 16 is represented as √16.
Mathematically, the square root of 16 is the number that, when multiplied by itself, gives 16:
\[\sqrt{16} = 4\]
Why is √16 Rational?
Since 16 is a perfect square (4 × 4 = 16), its square root is an integer. Rational numbers include all integers, fractions, and terminating decimals. Therefore, √16 is rational.
Calculation Methods
Several methods can be used to calculate the square root of 16:
- Long Division Method: This traditional method involves pairing digits from the right and finding the largest number that, when squared, gives the target number.
- Using a Calculator: Modern calculators provide a quick way to find square roots by pressing the √x key after entering the number.
- Computer Software: Programs like Excel or Google Sheets can calculate square roots using the SQRT function:
SQRT(16) = 4.
Conclusion
The square root of 16 is a rational number because it can be expressed as the integer 4. Understanding this concept helps in distinguishing between rational and irrational numbers in various mathematical contexts.

READ MORE:
Introduction
The concept of square roots is fundamental in mathematics, often leading to the question: is the square root of 16 rational or irrational? This article aims to clarify this by explaining the definitions and properties of rational and irrational numbers, and demonstrating why the square root of 16 is considered rational. Understanding this helps in recognizing patterns and applications in various mathematical contexts.
- Rational Numbers: These are numbers that can be expressed as a fraction of two integers, where the denominator is not zero.
- Irrational Numbers: These cannot be expressed as simple fractions. Their decimal expansions are non-repeating and non-terminating.
By delving into the nature of square roots and specifically examining the square root of 16, we reveal its classification as a rational number. This exploration will also touch upon methods of calculation and the significance of perfect squares in mathematics.
Definition of Rational and Irrational Numbers
To understand whether the square root of 16 is rational or irrational, we first need to define what rational and irrational numbers are.
- Rational Numbers: A rational number is any number that can be expressed as the quotient or fraction of two integers, \( \frac{a}{b} \), where \( a \) and \( b \) are integers and \( b \) is not zero. For example, \( \frac{1}{2} \), \( \frac{3}{4} \), and \( 5 \) (which can be written as \( \frac{5}{1} \)) are all rational numbers.
- Irrational Numbers: An irrational number, on the other hand, cannot be expressed as a simple fraction. These numbers have non-repeating, non-terminating decimal expansions. Examples of irrational numbers include \( \pi \) (pi) and \( \sqrt{2} \). Unlike rational numbers, their exact value cannot be precisely represented as a fraction.
To summarize:
| Rational Numbers | Irrational Numbers |
|---|---|
| Can be expressed as a fraction \( \frac{a}{b} \) | Cannot be expressed as a fraction |
| Decimals are either terminating or repeating | Decimals are non-terminating and non-repeating |
| Examples: \( \frac{1}{2}, 0.75, 5 \) | Examples: \( \pi, \sqrt{2} \) |
Why the Square Root of 16 is Rational
To determine why the square root of 16 is rational, we need to explore the characteristics of rational numbers and apply them to this specific case.
- Definition of Rational Numbers:
Rational numbers are those that can be expressed as the quotient or fraction of two integers, \( \frac{a}{b} \), where \( a \) and \( b \) are integers and \( b \neq 0 \).
- Square Root Calculation:
From the previous section, we know that the square root of 16 is 4. This can be written as:
\[
\sqrt{16} = 4
\] - Expression as a Fraction:
The number 4 can be expressed as a fraction of two integers:
\[
4 = \frac{4}{1}
\]Here, both 4 and 1 are integers, and the denominator is not zero. This fits the definition of a rational number.
- Verification:
To further verify, consider that if a number is a perfect square, its square root is an integer. Since 16 is a perfect square (4 × 4 = 16), its square root is also an integer, which is inherently rational.
Therefore, based on the definition and properties of rational numbers, we can confidently state that the square root of 16 is rational.
| Number | Square Root | Rational or Irrational |
|---|---|---|
| 16 | 4 | Rational |
| Non-perfect square (e.g., 2) | \(\sqrt{2}\) | Irrational |
Perfect Squares and Their Properties
Perfect squares are numbers that are the product of an integer multiplied by itself. Understanding their properties helps in identifying whether their square roots are rational or irrational.
- Definition of Perfect Squares:
A perfect square is a number that can be expressed as \( n^2 \), where \( n \) is an integer. For example, 1, 4, 9, 16, and 25 are perfect squares because they can be written as \( 1^2 \), \( 2^2 \), \( 3^2 \), \( 4^2 \), and \( 5^2 \) respectively.
- Properties of Perfect Squares:
- Integer Roots: The square root of a perfect square is always an integer. For instance, \( \sqrt{16} = 4 \).
- Non-negative: Perfect squares are always non-negative because the product of any integer with itself is non-negative.
- Pattern in Units Digit: The units digit of perfect squares often follows a pattern. For example, if a number ends in 0, 1, 4, 5, 6, or 9, its square will end in the same digits.
- Sum of Consecutive Odd Numbers: A perfect square can be represented as the sum of consecutive odd numbers. For example, \( 16 = 1 + 3 + 5 + 7 \).
- Rationality of Square Roots:
Since the square root of a perfect square is always an integer, and integers are rational numbers, the square roots of perfect squares are always rational. For instance:
Perfect Square Square Root Rationality 1 1 Rational 4 2 Rational 9 3 Rational 16 4 Rational 25 5 Rational
Understanding perfect squares and their properties not only helps in identifying rational square roots but also provides a deeper insight into number patterns and mathematical relationships.

Methods to Calculate the Square Root of 16
Calculating the square root of 16 can be done using various methods. Here are some common and effective techniques:
- Prime Factorization Method:
- Factorize 16 into its prime factors: \( 16 = 2 \times 2 \times 2 \times 2 = 2^4 \).
- Group the prime factors into pairs: \( 2^4 = (2^2) \times (2^2) \).
- Take the square root of each pair: \( \sqrt{(2^2) \times (2^2)} = 2 \times 2 = 4 \).
- Long Division Method:
The long division method is useful for finding square roots of numbers that are not perfect squares, but can also be applied to perfect squares.
- Write the number (16) under the long division symbol.
- Group the digits in pairs starting from the decimal point. Here, we have a single pair: (16).
- Find the largest number whose square is less than or equal to the leftmost pair. In this case, 4, since \( 4^2 = 16 \).
- Subtract the square of this number from the leftmost pair: \( 16 - 16 = 0 \).
- Bring down the next pair of digits (if any) and repeat the process. Since there are no more digits, the square root is 4.
- Using a Calculator:
Most modern calculators have a square root function. To find the square root of 16:
- Enter 16 on the calculator.
- Press the square root (√) button.
- The display will show 4, indicating that the square root of 16 is 4.
- Estimating and Refining:
This method involves making an initial guess and then refining it through averaging.
- Make an initial guess: Let's guess 4 (since \( 4 \times 4 = 16 \)).
- Refine the guess: If necessary, take the average of the guess and the quotient of the original number divided by the guess. Here, since our guess is accurate, no further refinement is needed.
By using these methods, we can confidently determine that the square root of 16 is 4, a rational number.
Long Division Method
The long division method is a systematic approach to finding the square root of a number, including perfect squares like 16. Here's a detailed, step-by-step explanation of how to use the long division method to calculate the square root of 16:
- Set up the number:
Write 16 under the long division symbol. Since 16 is a two-digit number, it will be grouped as a single pair (16).
- Find the largest square:
Identify the largest number whose square is less than or equal to the leftmost pair (16). In this case, 4, since \( 4^2 = 16 \).
- Divide and subtract:
- Write 4 above the long division bar.
- Multiply 4 by itself (4 × 4) and write 16 under the pair 16.
- Subtract 16 from 16, resulting in 0.
- Bring down pairs (if any):
Since there are no more digits to bring down, the process is complete. The result above the bar (4) is the square root of 16.
Here's a visual representation of the long division process:
| 4 | |
| 4 | |16 |
| -16 | |
| 0 |
Through this method, we determine that the square root of 16 is 4, confirming that it is a rational number.
Calculator and Computer Methods
Using calculators and computers to find the square root of a number, such as 16, is straightforward and efficient. Here are the steps to follow:
- Using a Calculator:
- Step 1: Turn on the calculator.
- Step 2: Enter the number 16.
- Step 3: Press the square root (√) button.
- Step 4: The display will show 4, indicating that the square root of 16 is 4.
- Using a Computer:
- Using a Standard Calculator App:
- Step 1: Open the calculator application on your computer.
- Step 2: Switch to scientific mode if necessary (this mode includes the square root function).
- Step 3: Enter 16 using the number keys.
- Step 4: Click on the square root (√) button.
- Step 5: The result displayed will be 4.
- Using Programming Languages:
Several programming languages allow you to calculate square roots easily. Here are examples in a few common languages:
- Python:
import math result = math.sqrt(16) print(result) # Output will be 4 - JavaScript:
let result = Math.sqrt(16); console.log(result); // Output will be 4 - Excel:
- Step 1: Open a new Excel spreadsheet.
- Step 2: Click on a cell and type
=SQRT(16). - Step 3: Press Enter. The cell will display 4.
- Python:
- Using a Standard Calculator App:
These methods confirm that the square root of 16 is 4, a rational number, providing quick and reliable results through technology.
Exponent Form
Expressing numbers in exponent form is a powerful mathematical technique that simplifies calculations, particularly when dealing with square roots. Let's explore how the square root of 16 can be represented using exponents.
- Understanding Exponentiation:
Exponentiation is a mathematical operation that involves raising a number (the base) to a power (the exponent). For example, \( 2^4 \) means \( 2 \times 2 \times 2 \times 2 = 16 \).
- Square Root as an Exponent:
The square root of a number can be expressed as an exponent. Specifically, the square root of a number \( x \) is the same as raising \( x \) to the power of \( \frac{1}{2} \). This is written as:
\[
\sqrt{x} = x^{\frac{1}{2}}
\] - Applying to 16:
We know that 16 can be written as \( 2^4 \). Therefore, the square root of 16 can be expressed as:
\[
\sqrt{16} = \sqrt{2^4} = (2^4)^{\frac{1}{2}}
\]Using the rule of exponents that states \( (a^m)^n = a^{m \cdot n} \), we can simplify this to:
\[
(2^4)^{\frac{1}{2}} = 2^{4 \cdot \frac{1}{2}} = 2^2 = 4
\] - Rationality of the Result:
Since \( 4 \) is an integer, and integers are rational numbers, the result confirms that the square root of 16 is rational.
Thus, using the exponent form provides a clear and concise method to calculate and verify that the square root of 16 is a rational number.

Simplification of Square Root of 16
The process of simplifying the square root of 16 involves breaking down the number into its prime factors and finding the square root. Here is a step-by-step explanation:
-
First, identify the prime factors of 16. Since 16 is a perfect square, it can be expressed as the product of prime numbers:
\[
16 = 2 \times 2 \times 2 \times 2 = 2^4
\] -
Next, apply the square root to the prime factorization of 16:
\[
\sqrt{16} = \sqrt{2^4}
\] -
Use the property of square roots that states \(\sqrt{a^b} = a^{\frac{b}{2}}\):
\[
\sqrt{2^4} = 2^{\frac{4}{2}} = 2^2
\] -
Simplify the exponent:
\[
2^2 = 4
\] -
Therefore, the square root of 16 simplifies to:
\[
\sqrt{16} = 4
\]
This simplification shows that the square root of 16 is a rational number because it can be expressed as an integer, 4.
| Number | Square Root | Rational/Irrational |
|---|---|---|
| 16 | 4 | Rational |
By understanding the process of simplification, it is clear that \(\sqrt{16}\) is rational, as it results in the integer 4, a number that can be expressed as a ratio of two integers (4/1).
Applications of Square Roots
Square roots have a wide range of applications across various fields. Understanding and calculating square roots is fundamental in mathematics and practical scenarios. Here are some key applications:
-
Geometry:
In geometry, square roots are used to determine the lengths of sides in right triangles, squares, and other polygons. For instance, the length of the diagonal of a square can be found using the square root of the sum of the squares of its sides.
-
Algebra:
Square roots are essential in solving quadratic equations. The quadratic formula involves square roots to find the solutions of equations of the form \(ax^2 + bx + c = 0\).
-
Physics:
In physics, square roots are used in various formulas, such as those involving the calculation of energy, wave speeds, and other phenomena that follow inverse square laws.
-
Engineering:
Engineers use square roots to calculate areas, volumes, and other properties of materials and structures. For example, the square root is used in stress and strain calculations in materials science.
-
Computer Science:
Square roots are used in algorithms for computer graphics, cryptography, and data analysis. Many optimization algorithms also rely on square root calculations.
-
Finance:
In finance, square roots are used to calculate standard deviation and variance, which are measures of volatility and risk in investment portfolios.
-
Daily Life:
Square roots appear in various daily life scenarios, such as calculating distances, areas, and in construction tasks where right angles and measurements are involved.
Below is an example of how square roots are applied using the Pythagorean theorem in determining the length of a ladder needed to reach a certain height:
| Base (a) | Height (b) | Hypotenuse (c) |
| 5 ft | 12 ft | \(\sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13\) ft |
Thus, a ladder that is 13 feet long is required to reach a height of 12 feet from a point 5 feet away from the building. This application showcases the practical use of square roots in real-world problem-solving.
Tìm hiểu về số hữu tỉ và vô tỉ qua video này. Khám phá các khái niệm và ví dụ cụ thể để hiểu rõ hơn về toán học.
16 Số Hữu Tỉ và Vô Tỉ
READ MORE:
Khám phá liệu căn bậc chính là số hữu tỉ hay vô tỉ trong video này. Video cung cấp giải thích chi tiết và dễ hiểu về khái niệm toán học này.
CĂN BẬC CHÍNH SỐ HỮU TỈ HAY VÔ TỈ