Topic square root of 1 half: The square root of 1/2, often represented as √(1/2) or 1/√2, is a mathematical concept that simplifies to √2/2. This value is significant in various mathematical and scientific applications, including geometry and algebra. Understanding its properties and how to simplify such expressions is essential for students and professionals alike.
Table of Content
- Understanding the Square Root of 1/2
- Introduction
- Understanding the Concept of Square Root
- Mathematical Representation of Square Root of 1/2
- Step-by-Step Simplification
- Properties of Square Roots
- Practical Examples and Applications
- Advanced Calculations
- FAQs and Common Questions
- YOUTUBE: Video giải thích tại sao x lũy thừa một phần hai có nghĩa là căn bậc hai. Tìm hiểu cách thức và lý do tại sao điều này đúng trong toán học.
Understanding the Square Root of 1/2
The square root of 1/2 can be expressed in different forms and calculated using various mathematical techniques. Below is a detailed explanation of the steps involved and different ways to represent this value.
Mathematical Expression
The square root of 1/2 is written as:
Simplifying the Expression
- Rewrite the expression using the property of radicals: \[ \sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} \]
- Simplify the numerator: \[ \frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}} \]
- Rationalize the denominator: \[ \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \]
Decimal Form
The decimal approximation of the square root of 1/2 is:
\[
\frac{\sqrt{2}}{2} \approx 0.7071
\]
Understanding the Steps
- When simplifying \(\sqrt{\frac{1}{2}}\), we use the property of square roots that allows us to separate the numerator and the denominator under the square root.
- Next, we simplify the square root of 1 to get 1, resulting in the expression \(\frac{1}{\sqrt{2}}\).
- To rationalize the denominator, we multiply by \(\frac{\sqrt{2}}{\sqrt{2}}\), which gives us \(\frac{\sqrt{2}}{2}\).
Applications
The square root of 1/2 appears frequently in trigonometry, particularly in calculations involving sine and cosine functions for 45-degree angles where both functions equal \(\frac{\sqrt{2}}{2}\).
Additional Resources
READ MORE:
Introduction
The square root of 1/2 is a fundamental concept in mathematics, particularly useful in various scientific and engineering applications. This concept often appears in contexts involving probability, geometry, and algebra. To understand it better, we can express the square root of 1/2 in several equivalent forms, and explore its properties and applications step-by-step.
- First, express the square root of 1/2 using the property of radicals: \(\sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}}\).
- Next, rationalize the denominator to eliminate the radical: \(\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\).
- In decimal form, this is approximately 0.7071, which is a useful approximation in practical calculations.
This method showcases how to handle the square root of fractions and rationalize denominators, a common technique in algebra to simplify expressions. Understanding these steps provides a solid foundation for more advanced mathematical problems and real-world applications.
Understanding the Concept of Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because 3 * 3 = 9. This concept is fundamental in mathematics and is widely used in various fields, including algebra, geometry, and calculus.
To denote the square root of a number \( x \), we use the radical symbol: \( \sqrt{x} \). If \( y \) is the square root of \( x \), then \( y \) satisfies the equation \( y^2 = x \). Square roots can be classified into two categories: perfect squares and non-perfect squares. Perfect squares are numbers like 1, 4, 9, 16, and 25, which have integer square roots. Non-perfect squares, such as 2, 3, 5, and 10, have irrational square roots that cannot be expressed as a simple fraction.
Calculating the square root of a fraction involves the same principles as calculating the square root of an integer. For instance, to find the square root of 1/2, we can express it as:
\[ \sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}} \]
Rationalizing the denominator, we multiply both the numerator and the denominator by \( \sqrt{2} \):
\[ \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2} \]
This gives us the simplified form of the square root of 1/2.
Understanding the properties of square roots and how to manipulate them is crucial for solving more complex mathematical problems. This knowledge is applied in various practical scenarios, such as physics calculations, engineering designs, and even financial models.
Mathematical Representation of Square Root of 1/2
The square root of \( \frac{1}{2} \) can be expressed and simplified using radical notation and rationalization techniques. Let's explore the step-by-step process:
- Start with the initial expression: \[ \sqrt{\frac{1}{2}} \]
- Apply the property of radicals, which allows us to separate the square root of a fraction into the quotient of the square roots: \[ \sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} \]
- Since the square root of 1 is 1, this simplifies to: \[ \frac{1}{\sqrt{2}} \]
- To rationalize the denominator, multiply the numerator and the denominator by \( \sqrt{2} \): \[ \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2} \]
Thus, the simplified form of the square root of \( \frac{1}{2} \) is:
\[
\frac{\sqrt{2}}{2} \approx 0.7071
\]
Step-by-Step Simplification
To simplify the square root of a fraction like \( \sqrt{\frac{1}{2}} \), follow these detailed steps:
Rewrite the square root of the fraction:
\[
\sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}}
\]Simplify the numerator and the denominator:
\[
\frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}}
\]Rationalize the denominator to eliminate the square root in the denominator. Multiply both the numerator and the denominator by \( \sqrt{2} \):
\[
\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]The simplified form of \( \sqrt{\frac{1}{2}} \) is:
\[
\sqrt{\frac{1}{2}} = \frac{\sqrt{2}}{2}
\]
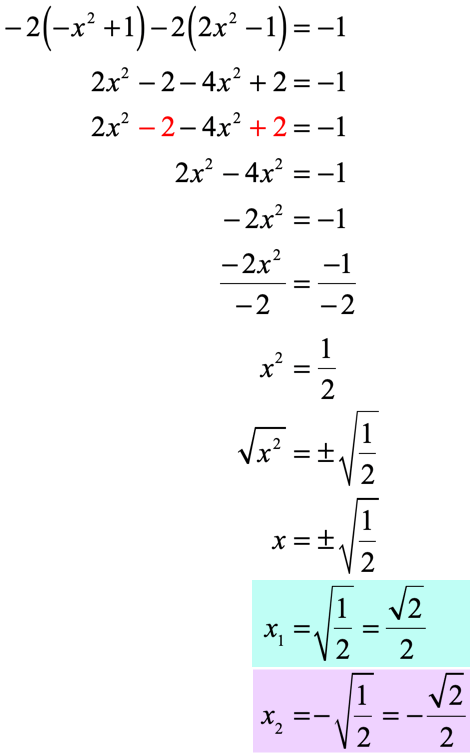
Properties of Square Roots
Understanding the properties of square roots is crucial in various mathematical calculations. These properties simplify complex expressions and make solving equations more manageable.
- Product Property: The square root of a product is equal to the product of the square roots of the factors. In mathematical terms, this is expressed as \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and denominator. This is written as \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
- Power Property: The square root of a number raised to any power is equal to the number raised to half that power, shown as \( \sqrt{a^n} = a^{\frac{n}{2}} \).
- Conjugate Property: The conjugate of a binomial with a square root is used to rationalize denominators, written as \( (a + \sqrt{b})(a - \sqrt{b}) = a^2 - b \).
- Additive Property: This property is used less frequently but states that \( \sqrt{a} + \sqrt{b} \) is not necessarily equal to \( \sqrt{a + b} \).
These properties are fundamental in simplifying expressions and solving equations involving square roots. By mastering these properties, students and professionals can handle a wide range of mathematical challenges more effectively.
Practical Examples and Applications
Understanding the practical applications of the square root of 1/2 helps in various fields such as physics, engineering, and finance. Here are some detailed examples and step-by-step explanations:
-
Engineering and Physics:
Square roots are essential in calculating distances, areas, and in solving various equations. For example, in the Pythagorean theorem, if one of the legs of a right triangle is 1 unit and the hypotenuse is \(\sqrt{2}\) units, then the other leg must be \(\sqrt{1/2}\) units, illustrating the practical application of the square root of 1/2 in real-world geometry.
-
Finance:
Square roots are used to calculate the standard deviation and variance in finance, which are critical for assessing investment risks. For instance, the annualized return rate can be calculated using the square root formula.
-
Architecture:
In architecture, square roots help in determining the proportions of structures. For example, if a rectangular space has an area of 1/2 square units, the length of each side can be found using the square root of 1/2.
-
Computer Graphics:
Square roots are often used in algorithms for rendering images and calculating distances between points in a 2D or 3D space. This is crucial for creating realistic graphics and animations.
Advanced Calculations
In this section, we will explore advanced calculations involving the square root of 1/2. Understanding these calculations requires familiarity with algebraic manipulations, trigonometry, and complex numbers. Let's delve into these concepts step by step.
1. Algebraic Manipulations
The square root of 1/2 can be expressed in its simplest form using rationalization:
\[\sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\]
This simplifies to:
\[\frac{\sqrt{2}}{2}\]
2. Trigonometric Representation
The square root of 1/2 often appears in trigonometry, particularly with sine and cosine functions. For instance:
\[\sin(45^\circ) = \cos(45^\circ) = \frac{\sqrt{2}}{2}\]
3. Using Complex Numbers
In the context of complex numbers, the square root of 1/2 can be represented as a complex number in polar form. Consider the complex number \(z\) such that:
\[z = re^{i\theta}\]
For \(\frac{1}{\sqrt{2}}\), we can write:
\[\frac{1}{\sqrt{2}} = e^{i\frac{\pi}{4}}\]
since \(\cos(\frac{\pi}{4}) + i\sin(\frac{\pi}{4}) = \frac{\sqrt{2}}{2} + i\frac{\sqrt{2}}{2}\). Therefore:
\[\frac{1}{\sqrt{2}} = e^{i\frac{\pi}{4}}\]
4. Calculating Powers and Roots
Calculating powers and roots of the square root of 1/2 can also be insightful. Consider the expression \(\left(\frac{\sqrt{2}}{2}\right)^n\):
- For \(n=2\):
\[\left(\frac{\sqrt{2}}{2}\right)^2 = \frac{2}{4} = \frac{1}{2}\]
- For \(n=3\):
\[\left(\frac{\sqrt{2}}{2}\right)^3 = \frac{2^{3/2}}{8} = \frac{\sqrt{8}}{8} = \frac{2\sqrt{2}}{8} = \frac{\sqrt{2}}{4}\]
5. Square Roots in Different Bases
Calculating the square root of 1/2 in different bases can provide deeper insights. Let's consider base \(b\):
\[\sqrt{\frac{1}{2}}_b = \frac{\sqrt{1_b}}{\sqrt{2_b}}\]
Here, the calculations will depend on the base conversion and subsequent simplification.
6. Matrix Representation
The square root of 1/2 can also be represented and manipulated within matrices. For example, consider a rotation matrix in 2D space that uses \(\frac{\sqrt{2}}{2}\) as its elements:
| \[\begin{bmatrix} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{bmatrix}\] |
This matrix represents a 45-degree rotation in the plane.
7. Practical Application in Engineering
In engineering, the square root of 1/2 is often used in signal processing, particularly in Fourier transforms and filtering:
\[\text{Filter Coefficient} = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} e^{-\frac{x^2}{2}} dx = \frac{1}{\sqrt{2}}\]
This is a Gaussian function where the normalization factor involves the square root of 1/2.
These advanced calculations illustrate the versatility and importance of the square root of 1/2 across various mathematical and engineering disciplines.
FAQs and Common Questions
-
What is the square root of 1/2?
The square root of 1/2 can be expressed as \(\sqrt{\frac{1}{2}}\). Simplifying this, we get \(\sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\).
-
How do you find the square root of a fraction?
To find the square root of a fraction, you take the square root of the numerator and the denominator separately. For example, \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
-
Why is the square root of 1/2 written as \(\frac{\sqrt{2}}{2}\)?
This is a simplification process to avoid having a square root in the denominator. Multiplying both the numerator and the denominator by \(\sqrt{2}\), we get \(\frac{1 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} = \frac{\sqrt{2}}{2}\).
-
What are the applications of the square root of 1/2?
The square root of 1/2 is used in various mathematical contexts, including trigonometry where it represents the sine or cosine of a 45-degree angle. It's also found in physics, engineering, and computer graphics.
-
How do you use the square root of 1/2 in equations?
In equations, the square root of 1/2 is often used to simplify expressions involving square roots. For instance, in solving quadratic equations or working with wave functions in quantum mechanics, you might encounter this value.
-
Can the square root of 1/2 be represented in decimal form?
Yes, the square root of 1/2 in decimal form is approximately 0.7071.
-
What is the significance of \(\sqrt{2}\) in the square root of 1/2?
The number \(\sqrt{2}\) is an irrational number approximately equal to 1.414. When divided by 2, it represents the simplified form of the square root of 1/2, which is \(\frac{\sqrt{2}}{2}\).
-
Why is it important to simplify square roots?
Simplifying square roots helps in making calculations easier and expressions more manageable. It is especially important in higher mathematics, physics, and engineering.

Video giải thích tại sao x lũy thừa một phần hai có nghĩa là căn bậc hai. Tìm hiểu cách thức và lý do tại sao điều này đúng trong toán học.
Tại sao "x lũy thừa một phần hai" có nghĩa là căn bậc hai?
READ MORE:
Video giải thích tại sao căn bậc hai được biểu diễn bằng lũy thừa 1/2. Khám phá lý do và cách thức điều này trong toán học.
Tại sao căn bậc hai là lũy thừa 1/2?














