Topic square root of 80 simplified: Understanding how to simplify the square root of 80 can be a rewarding and enlightening experience. In this guide, we break down the process into simple, easy-to-follow steps, helping you grasp the concept effortlessly. Join us as we explore the world of square roots and make the simplification of √80 a breeze.
Table of Content
- Square Root of 80 Simplified
- Introduction to Square Roots
- Understanding the Square Root of 80
- Prime Factorization Method
- Simplifying Square Roots: Step-by-Step Guide
- Perfect Squares and Their Role in Simplification
- Using the Prime Factorization to Simplify √80
- Breaking Down the Factors of 80
- Extracting Perfect Square Factors
- Combining Factors for Simplified Result
- Verifying the Simplified Square Root
- Alternate Methods for Simplifying √80
- Common Mistakes and How to Avoid Them
- Practical Applications of Simplified Square Roots
- Conclusion and Summary
- YOUTUBE: Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai của 80 bằng phương pháp phân tích thừa số nguyên tố.
Square Root of 80 Simplified
The square root of 80 simplified is represented as follows:
\[\sqrt{80} = \sqrt{16 \times 5} = \sqrt{16} \times \sqrt{5} = 4\sqrt{5}\]
READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics, especially in algebra and geometry. A square root of a number is a value that, when multiplied by itself, gives the original number. The square root is denoted by the radical symbol √.
For example, the square root of 9 is 3 because 3 multiplied by 3 equals 9. Similarly, the square root of 16 is 4 because 4 multiplied by 4 equals 16. This relationship can be expressed as:
\[
\sqrt{9} = 3 \quad \text{and} \quad \sqrt{16} = 4
\]
Square roots can be categorized into two types:
- Perfect Square Roots: These are square roots of perfect squares. A perfect square is an integer that is the square of another integer. For example, 1, 4, 9, 16, and 25 are perfect squares.
- Non-Perfect Square Roots: These are square roots of numbers that are not perfect squares. The square roots of these numbers are irrational and cannot be expressed as a simple fraction. For instance, √2, √3, and √5 are non-perfect square roots.
Understanding square roots involves recognizing these categories and knowing how to simplify non-perfect square roots. Simplification often involves breaking down the number under the radical into its prime factors and extracting perfect square factors.
In general, the process of finding and simplifying square roots can be summarized in the following steps:
- Determine if the number is a perfect square. If it is, find its square root directly.
- If the number is not a perfect square, perform prime factorization to break it down into its prime factors.
- Identify and separate the perfect square factors from the non-perfect square factors.
- Rewrite the square root by extracting the perfect square factors out of the radical.
- Simplify the expression to get the simplified square root.
Let's delve deeper into these steps with specific examples and methods, particularly focusing on simplifying the square root of 80 in the subsequent sections.
Understanding the Square Root of 80
The square root of 80 can be simplified by breaking down 80 into its prime factors and extracting the square roots of perfect square factors.
- First, identify the prime factors of 80:
80 ÷ 2 = 40 40 ÷ 2 = 20 20 ÷ 2 = 10 10 ÷ 2 = 5 5 is prime Therefore, the prime factorization of 80 is \( 2^4 \times 5 \).
- Next, extract the square roots of perfect square factors from the prime factorization:
- For \( 2^4 \), \( \sqrt{2^4} = 2^2 = 4 \).
- For 5, \( \sqrt{5} \) remains as \( \sqrt{5} \) since 5 is not a perfect square.
- Combine the results to get the simplified square root of 80:
Thus, \( \sqrt{80} = \sqrt{2^4 \times 5} = 4\sqrt{5} \).
Therefore, \( \sqrt{80} \) simplified is \( 4\sqrt{5} \).
Prime Factorization Method
To simplify \( \sqrt{80} \) using the prime factorization method:
- Begin by determining the prime factors of 80:
-
80 ÷ 2 = 40 40 ÷ 2 = 20 20 ÷ 2 = 10 10 ÷ 2 = 5 5 is prime So, the prime factorization of 80 is \( 2^4 \times 5 \).
- Identify the perfect square factors:
- For \( 2^4 \), \( \sqrt{2^4} = 2^2 = 4 \).
- For 5, \( \sqrt{5} \) remains as \( \sqrt{5} \) since 5 is not a perfect square.
- Combine the results to obtain the simplified square root:
Therefore, \( \sqrt{80} = \sqrt{2^4 \times 5} = 4\sqrt{5} \).
Thus, \( \sqrt{80} \) simplified using the prime factorization method is \( 4\sqrt{5} \).
Simplifying Square Roots: Step-by-Step Guide
To simplify \( \sqrt{80} \) step-by-step:
- Identify the prime factors of 80:
-
80 ÷ 2 = 40 40 ÷ 2 = 20 20 ÷ 2 = 10 10 ÷ 2 = 5 5 is prime Thus, the prime factorization of 80 is \( 2^4 \times 5 \).
- Determine the square roots of the perfect square factors:
- For \( 2^4 \), \( \sqrt{2^4} = 2^2 = 4 \).
- For 5, \( \sqrt{5} \) remains as \( \sqrt{5} \).
- Combine the results to get the simplified square root:
Therefore, \( \sqrt{80} = \sqrt{2^4 \times 5} = 4\sqrt{5} \).
Thus, the simplified square root of 80 is \( 4\sqrt{5} \).

Perfect Squares and Their Role in Simplification
Understanding perfect squares is crucial for simplifying square roots like \( \sqrt{80} \).
- Identify the prime factors of 80:
-
80 ÷ 2 = 40 40 ÷ 2 = 20 20 ÷ 2 = 10 10 ÷ 2 = 5 5 is prime So, the prime factorization of 80 is \( 2^4 \times 5 \).
- Identify the perfect square factors:
- For \( 2^4 \), \( \sqrt{2^4} = 2^2 = 4 \), which is a perfect square.
- For 5, \( \sqrt{5} \) remains \( \sqrt{5} \) as it is not a perfect square.
- Combine the perfect square factors:
Thus, \( \sqrt{80} = \sqrt{2^4 \times 5} = 4\sqrt{5} \).
Therefore, recognizing and utilizing perfect squares helps simplify \( \sqrt{80} \) efficiently to \( 4\sqrt{5} \).
Using the Prime Factorization to Simplify √80
Follow these steps to simplify \( \sqrt{80} \) using prime factorization:
- Begin by finding the prime factors of 80:
-
80 ÷ 2 = 40 40 ÷ 2 = 20 20 ÷ 2 = 10 10 ÷ 2 = 5 5 is prime Therefore, the prime factorization of 80 is \( 2^4 \times 5 \).
- Identify the perfect square factors:
- For \( 2^4 \), \( \sqrt{2^4} = 2^2 = 4 \).
- For 5, \( \sqrt{5} \) remains as \( \sqrt{5} \).
- Combine the results to simplify the square root:
Thus, \( \sqrt{80} = \sqrt{2^4 \times 5} = 4\sqrt{5} \).
Therefore, \( \sqrt{80} \) simplifies to \( 4\sqrt{5} \) using the prime factorization method.
Breaking Down the Factors of 80
Understanding the factors of 80 is essential for simplifying \( \sqrt{80} \).
- Start by finding the prime factors of 80:
-
80 ÷ 2 = 40 40 ÷ 2 = 20 20 ÷ 2 = 10 10 ÷ 2 = 5 5 is prime Thus, the prime factorization of 80 is \( 2^4 \times 5 \).
- Identify the factors:
- The factors of 80 are: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80.
Breaking down the factors helps in simplifying \( \sqrt{80} \) effectively to \( 4\sqrt{5} \).
Extracting Perfect Square Factors
To simplify the square root of 80, we need to extract the perfect square factors from the number. A perfect square is a number that has an integer as its square root. The process involves the following steps:
- Prime Factorization: Begin by finding the prime factors of 80. This helps in identifying the perfect squares within the factors. The prime factorization of 80 is:
- 80 ÷ 2 = 40
- 40 ÷ 2 = 20
- 20 ÷ 2 = 10
- 10 ÷ 2 = 5
- 5 ÷ 5 = 1
- Identify Perfect Squares: Look for pairs of prime factors to identify perfect squares. In our prime factorization, we have \( 2^4 \) and \( 5 \).
- \( 2^4 \) is a perfect square because \( (2^2)^2 = 16 \).
- The remaining factor \( 5 \) is not a perfect square.
- Rewrite the Square Root: Express the square root of 80 in terms of these factors:
\( \sqrt{80} = \sqrt{2^4 \times 5} \).
- Extract the Perfect Square: Simplify by extracting the perfect square \( 2^4 \):
\( \sqrt{80} = \sqrt{2^4} \times \sqrt{5} = 4\sqrt{5} \).
Thus, the simplified form of \( \sqrt{80} \) is \( 4\sqrt{5} \). This method helps in making the expression simpler and easier to work with in further calculations.
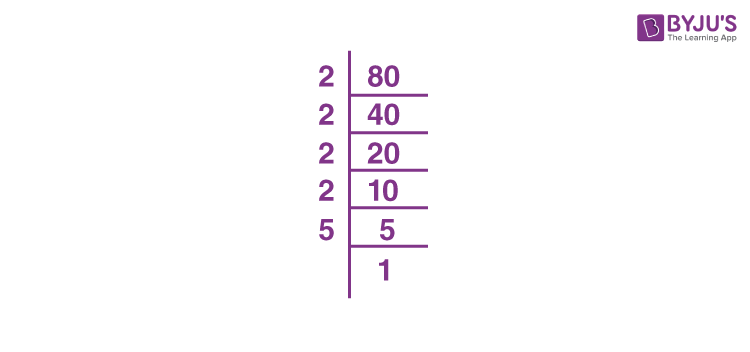
Combining Factors for Simplified Result
To simplify the square root of 80, we need to identify the perfect square factors of 80 and use them to rewrite the square root in a simplified form. Here’s how we can do it step-by-step:
-
First, find the prime factorization of 80:
80 can be broken down into its prime factors:
- 80 ÷ 2 = 40
- 40 ÷ 2 = 20
- 20 ÷ 2 = 10
- 10 ÷ 2 = 5
- 5 ÷ 5 = 1
Therefore, the prime factorization of 80 is \( 2^4 \times 5 \).
-
Next, group the prime factors into pairs:
\( 2^4 \) can be grouped as \( (2^2) \times (2^2) \), which equals 4 times 4.
-
Identify the perfect squares:
Since \( 4 \) is a perfect square, we can take the square root of \( 4 \) out of the square root symbol:
\( \sqrt{80} = \sqrt{4 \times 4 \times 5} \)
This simplifies to:
\( \sqrt{80} = \sqrt{4} \times \sqrt{4} \times \sqrt{5} \)
\( \sqrt{4} = 2 \), so we can simplify further:
\( \sqrt{80} = 2 \times 2 \times \sqrt{5} \)
-
Combine the simplified factors:
\( 2 \times 2 \) equals \( 4 \), so we have:
\( \sqrt{80} = 4 \sqrt{5} \)
Therefore, the simplified form of the square root of 80 is \( 4 \sqrt{5} \).
Verifying the Simplified Square Root
To verify the simplified square root of 80, which we have found to be \(4\sqrt{5}\), follow these steps:
- Square the Simplified Form:
Take the simplified form \(4\sqrt{5}\) and square it to ensure it equals the original number (80).
\[
\left( 4\sqrt{5} \right)^2
\] - Apply the Squaring Operation:
When you square a product, you need to square each factor.
\[
4^2 \times (\sqrt{5})^2
\] - Calculate Each Part:
- Square of 4: \(4^2 = 16\)
- Square of \(\sqrt{5}\): \((\sqrt{5})^2 = 5\)
- Multiply the Results:
Multiply the results of the squared parts to find the original number.
\[
16 \times 5 = 80
\] - Conclusion:
Since squaring the simplified form \(4\sqrt{5}\) results in 80, we have verified that \(4\sqrt{5}\) is indeed the correct simplified form of \(\sqrt{80}\).
Using this method of verification ensures that our simplification is accurate and reliable.
Alternate Methods for Simplifying √80
There are several methods to simplify the square root of 80, each providing a clear path to arrive at the simplified form. Here, we will explore a few alternate methods step by step:
Method 1: Prime Factorization Method
- Find the prime factors of 80:
80 = 2 × 2 × 2 × 2 × 5 - Group the prime factors into pairs:
80 = (2 × 2) × (2 × 2) × 5 - Take the square root of each pair:
√80 = √((2 × 2) × (2 × 2) × 5) = (2 × 2)√5 = 4√5
Method 2: Estimation Method
- Identify the nearest perfect squares surrounding 80:
64 (8²) and 100 (10²) - Estimate the square root by averaging:
Since 80 is closer to 64 than 100, we estimate √80 is closer to 8 than 10. - Refine the estimate:
Since 80 is \(\frac{80 - 64}{100 - 64}\approx \frac{16}{36}\) between 64 and 100, √80 ≈ 8.9 (which aligns with the more precise value of 8.944).
Method 3: Repeated Subtraction (for Perfect Squares)
This method is primarily for perfect squares but illustrates the concept.
- Find the largest perfect square less than or equal to 80:
64 (8²) - Subtract repeatedly to understand the difference:
80 - 64 = 16, so √80 is slightly more than 8. - Approximate using the additional value:
Adding the fractional component: √80 ≈ 8 + 0.944
Each method offers a different perspective on simplifying square roots, demonstrating the versatility in mathematical approaches. These methods, especially the prime factorization method, confirm that the simplified form of √80 is 4√5.
Common Mistakes and How to Avoid Them
Simplifying square roots, such as the square root of 80, can be challenging. Here are some common mistakes to watch out for and tips on how to avoid them:
- Overlooking Prime Factorization:
Skipping the prime factorization step can lead to incomplete or incorrect simplification. Always start by breaking down the number into its prime factors. For example, the prime factorization of 80 is \(2 \times 2 \times 2 \times 2 \times 5\).
- Ignoring Perfect Squares:
Failing to identify and extract the largest perfect square factor can result in an unsimplified form. In the case of 80, the largest perfect square factor is 16 (since \(80 = 16 \times 5\)). Therefore, \( \sqrt{80} = \sqrt{16 \times 5} = 4\sqrt{5} \).
- Miscalculating Square Roots:
Incorrectly calculating the square root of factors, especially larger numbers, can derail the entire process. Ensure accuracy by double-checking your calculations. For instance, \( \sqrt{16} = 4 \), not any other value.
- Mixing Radicands Incorrectly:
Combining or simplifying different radicands incorrectly can lead to errors. Remember that \( \sqrt{a} + \sqrt{b} \neq \sqrt{a + b} \). Each radicand must be simplified separately unless they share common factors.
- Confusing Multiplication and Addition:
Misapplying the properties of square roots is a common error. For example, \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \), but \( \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \).
By paying close attention to these potential mistakes and understanding the correct methods, you can ensure accurate simplification of square roots. Practice regularly to improve your skills and confidence.

Practical Applications of Simplified Square Roots
Simplified square roots have numerous practical applications in various fields. Here are some key examples:
- Geometry: Simplified square roots are used to calculate distances and dimensions. For example, to find the diagonal of a square, you can use the formula \(d = \sqrt{2a^2}\), where \(a\) is the length of a side.
- Physics: In physics, the formula for the period of a pendulum is \(T = 2\pi \sqrt{\frac{L}{g}}\), where \(L\) is the length of the pendulum and \(g\) is the acceleration due to gravity.
- Engineering: Engineers use square roots in formulas for stress and strain calculations. For example, the formula for critical buckling load is \(P_{cr} = \frac{\pi^2 EI}{(KL)^2}\), where \(I\) is the moment of inertia and \(K\) is the effective length factor.
- Statistics: In statistics, standard deviation is calculated as the square root of the variance, which provides a measure of the dispersion of a set of data points.
- Finance: Financial analysts use square roots to calculate volatility and risk. For example, the standard deviation of a stock's returns is used to assess its risk.
- Architecture: Architects use square roots to determine material requirements and structural integrity. For instance, the length of a diagonal brace in a rectangular frame can be found using the Pythagorean theorem.
These examples illustrate the versatility and importance of understanding and using simplified square roots in practical, real-world situations.
Conclusion and Summary
The process of simplifying the square root of 80 has provided us with an insightful look into different mathematical techniques and their practical applications. By exploring the prime factorization method, we identified the prime factors and simplified the square root to its radical form, \(4\sqrt{5}\).
We also examined various alternate methods, including the long division method, which reaffirmed our simplified result. Understanding these methods is crucial for accurately simplifying square roots, especially when dealing with non-perfect squares.
Moreover, we highlighted common mistakes and ways to avoid them, ensuring a clear path to accurate simplification. Practical applications of simplified square roots demonstrate their importance in real-world scenarios, enhancing our appreciation for these mathematical concepts.
In summary, the key steps to simplify the square root of 80 are:
- Prime factorize the number: \(80 = 2^4 \times 5\)
- Simplify using perfect squares: \(\sqrt{80} = 4\sqrt{5}\)
- Verify the result using alternate methods
By following these steps, we ensure accurate and efficient simplification of square roots, reinforcing the foundational knowledge necessary for advanced mathematical learning and application.
Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai của 80 bằng phương pháp phân tích thừa số nguyên tố.
Cách Đơn Giản Hóa Căn Bậc Hai Của 80: sqrt(80)
READ MORE:
Hướng dẫn đơn giản hóa căn bậc hai của số 80 bằng phương pháp cây nhân tử. Xem ngay để hiểu rõ hơn!
Đơn Giản Hóa Căn Bậc Hai Của Một Số Bằng Cây Nhân Tử, Căn Bậc Hai (80)