Square Root of 7: Rational or Irrational - A Detailed Exploration

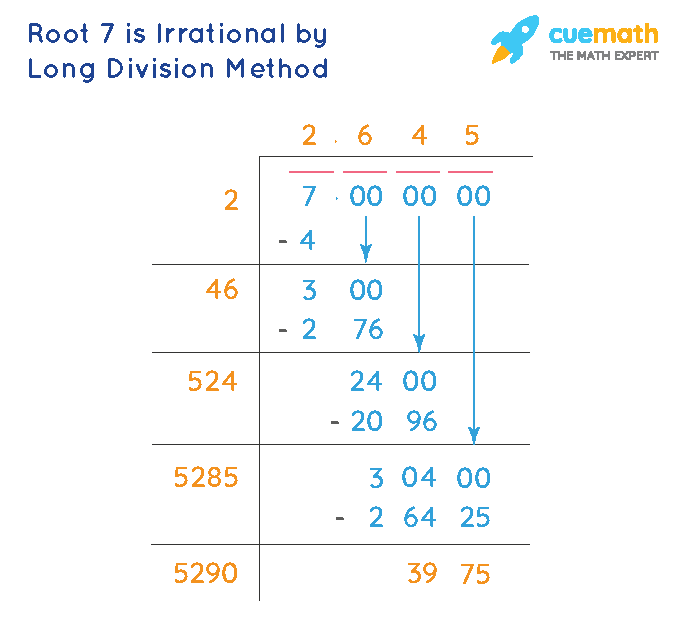
The square root of 7 is an irrational number.

To determine whether the square root of 7 is rational or irrational, we analyze its decimal representation and its divisibility properties.

The square root of 7 can be expressed as \( \sqrt{7} \).

Upon evaluating, it is found that \( \sqrt{7} \approx 2.6457513110645906 \).

It is a non-repeating, non-terminating decimal, which is a characteristic of irrational numbers.

Therefore, the square root of 7 is definitively categorized as an irrational number.

A square root of a number \( x \) is another number \( y \) such that \( y^2 = x \). Specifically, the square root of 7, denoted as \( \sqrt{7} \), seeks to determine whether it can be expressed as a fraction of two integers (rational) or not (irrational). Through mathematical exploration, it has been established that \( \sqrt{7} \) is indeed an irrational number.

Rational numbers are those that can be expressed as the quotient or fraction \( \frac{p}{q} \), where \( p \) and \( q \) are integers and \( q \neq 0 \). Examples include 0, 1, -5, \( \frac{2}{3} \), etc. On the other hand, irrational numbers cannot be represented as fractions and have non-terminating, non-repeating decimal expansions. The square root of 7 (\( \sqrt{7} \)) is a classic example of an irrational number, demonstrating that not all numbers are rational.

Rational numbers are numbers that can be expressed as the ratio of two integers \( \frac{p}{q} \), where \( q \neq 0 \). They can be positive, negative, or zero and can include integers and fractions such as \( -3, 0, \frac{1}{2}, \) etc. The set of rational numbers is closed under addition, subtraction, multiplication, and division (except division by zero), making them fundamental in arithmetic and algebraic operations.

Irrational numbers are real numbers that cannot be expressed as a simple fraction or the ratio of two integers. Unlike rational numbers, which can be written as a/b where a and b are integers and b ≠ 0, irrational numbers have non-repeating, non-terminating decimal expansions.

Some of the key properties of irrational numbers include:

• Non-terminating and Non-repeating Decimal Representation: Irrational numbers have decimal expansions that go on forever without repeating. For example, the decimal representation of π (pi) is approximately 3.14159... and it never ends or repeats.
• Incommensurability: Irrational numbers cannot be expressed as a ratio of two integers. There is no fraction or exact decimal that can represent an irrational number.
• Closure Under Addition and Multiplication: The sum or product of a rational number and an irrational number is always irrational. However, the sum or product of two irrational numbers can be either rational or irrational.
• Density: Between any two rational numbers, there are infinitely many irrational numbers. This means that irrational numbers are densely packed along the number line.

Some well-known examples of irrational numbers include:

• π (Pi)
• e (Euler's Number)
• √2 (Square Root of 2)
• √3 (Square Root of 3)
• Golden Ratio (φ)

To further illustrate the concept, consider the square root of a prime number. The square root of any prime number is irrational. For example, the square root of 7 is an irrational number, as it cannot be expressed as a fraction and its decimal representation is non-terminating and non-repeating.

The square root of 7, denoted as \( \sqrt{7} \), is a number which, when multiplied by itself, equals 7. This concept can be understood through the general definition of a square root, where for any non-negative number \( x \), the square root of \( x \) is a number \( y \) such that \( y^2 = x \).

In the case of 7, we seek a number \( y \) such that \( y^2 = 7 \). While simple numbers like 4 have integer square roots (since \( 2^2 = 4 \)), not all numbers have such straightforward roots. The square root of 7 is an example of this, as it cannot be expressed as a simple fraction or integer.

To explore why \( \sqrt{7} \) is unique, let's delve into its nature through a few key points:

• Non-integer Value: The square root of 7 is not an integer. It lies between 2 and 3, closer to 2.6457513110645906, but it is not a precise decimal number.
• Decimal Representation: The decimal expansion of \( \sqrt{7} \) is non-repeating and non-terminating. This is a hallmark of irrational numbers, indicating that it cannot be exactly represented as a fraction.
• Irrational Number: By definition, an irrational number cannot be written as a ratio of two integers. The square root of 7 fits this description perfectly, meaning it is irrational.

In mathematical terms, the irrationality of \( \sqrt{7} \) can be proven using a method of contradiction. The proof starts by assuming that \( \sqrt{7} \) is rational, meaning it can be written as \( \frac{a}{b} \) where \( a \) and \( b \) are integers with no common factors other than 1 (in simplest form). Following this assumption to its logical conclusion leads to a contradiction, thus proving that \( \sqrt{7} \) cannot be rational.

The importance of recognizing the nature of \( \sqrt{7} \) extends beyond theoretical mathematics. Irrational numbers like \( \sqrt{7} \) play a crucial role in various fields, including geometry, calculus, and complex number theory. They help mathematicians understand the continuity of the real number line and the behavior of functions across different domains.

In summary, the square root of 7 is a fascinating example of an irrational number. Its non-repeating, non-terminating decimal expansion and inability to be expressed as a fraction underscore its unique place in the realm of mathematics. Understanding its nature helps us appreciate the broader landscape of number theory and the intricate structure of the numbers we use every day.

The proof that the square root of 7 is irrational can be conducted using a method called proof by contradiction. This method demonstrates that if we assume the square root of 7 is rational, we arrive at a contradiction. Here is a detailed step-by-step proof:

1. Assume that $\sqrt{7}$ is a rational number. By definition, a rational number can be expressed as a fraction $\frac{p}{q}$ where p and q are integers that have no common factors other than 1 (i.e., they are coprime) and q is not zero.

2. Then, we can write:

   $\sqrt{7}=\frac{p}{q}$

   Squaring both sides, we get:

   $7\; =\frac{p^2}{q^2}$

   Which simplifies to:

   $7q^2=p^2$

3. This implies that $p^2$ is a multiple of 7. Therefore, p must also be a multiple of 7 (since 7 is a prime number).

   Let $p=\; 7k$ for some integer k.

4. Substitute $p=\; 7k$ into the equation $7q^2=p^2$:

   $7q^2={\left(}^k$

   This simplifies to:

   $7q^2=\; 49k^2$

   Divide both sides by 7:

   $q^2=\; 7k^2$

5. This implies that $q^2$ is a multiple of 7. Therefore, q must also be a multiple of 7.

6. We have now shown that both p and q are multiples of 7, which contradicts our initial assumption that p and q have no common factors other than 1.

   Therefore, the assumption that $\sqrt{7}$ is rational must be false.

7. Hence, the square root of 7 is irrational.

The concept of irrational numbers dates back to ancient Greece. The discovery of irrational numbers is often attributed to Hippasus of Metapontum, a member of the Pythagorean school of thought. Legend has it that Hippasus discovered the existence of irrational numbers while trying to determine the length of the diagonal of a unit square. This discovery contradicted the Pythagorean belief that all numbers could be expressed as the ratio of two integers.

The Pythagoreans held the belief that numbers were the foundation of all reality, and this philosophical stance made the discovery of irrational numbers quite controversial. It is said that the Pythagoreans were so disturbed by Hippasus's findings that they ostracized him, and some stories even suggest that he was drowned at sea as punishment for revealing the existence of irrational numbers.

The irrationality of numbers like the square root of 7 underscores the complexity and richness of the number system. Unlike rational numbers, which have decimal representations that terminate or repeat, irrational numbers have non-terminating, non-repeating decimal expansions. The square root of 7, approximately 2.6457513110645906, continues infinitely without repeating, highlighting its irrational nature.

In the context of mathematical importance, irrational numbers play a crucial role in various fields. They are essential in geometry, particularly in the study of figures like circles and triangles, where lengths and distances often involve irrational numbers. The discovery of irrational numbers also paved the way for further mathematical advancements, including the development of real number theory and calculus.

Understanding irrational numbers like the square root of 7 helps in appreciating the diversity within the number system. It illustrates that even within the infinite set of numbers, there are complexities that challenge our intuitions and expand our understanding of mathematics.

Overall, the historical context of irrational numbers and their mathematical significance underscore the importance of recognizing and embracing the full spectrum of numbers, from the simple to the complex.

Irrational numbers play a crucial role in various branches of mathematics and have numerous practical applications. Below are some significant applications of irrational numbers:

• Geometry and Trigonometry:

  Irrational numbers often appear in geometric calculations. For instance, the length of the diagonal of a square with side length 1 is \(\sqrt{2}\), an irrational number. Similarly, the golden ratio \(\phi\) (approximately 1.618) is an irrational number that appears in the proportions of various geometric figures and in the study of Fibonacci sequences.

• Calculus and Analysis:

  Irrational numbers are fundamental in calculus, particularly in the study of limits, derivatives, and integrals. For example, the number \(e\) (approximately 2.718) is an irrational number that serves as the base of natural logarithms and is crucial in exponential growth and decay problems.

• Mathematical Constants:

  Several important mathematical constants are irrational numbers. The most famous is \(\pi\) (approximately 3.14159), which represents the ratio of a circle's circumference to its diameter. \(\pi\) is essential in formulas for areas and volumes of various geometric shapes.

• Algebra and Number Theory:

  In number theory, the study of irrational numbers helps in understanding the properties of integers and rational numbers. For instance, the irrationality of \(\sqrt{n}\) (for non-square integers \(n\)) is a fundamental result that influences various theorems and proofs.

• Fractals and Chaos Theory:

  Irrational numbers are used in the generation and analysis of fractals. Fractals often exhibit self-similarity and intricate patterns that are described using irrational numbers. In chaos theory, irrational numbers help in understanding the unpredictable behavior of dynamical systems.

• Quantum Mechanics:

  In physics, particularly in quantum mechanics, irrational numbers appear in wave functions and the Heisenberg uncertainty principle. These numbers are essential for describing the probabilistic nature of particles at the quantum level.

The presence of irrational numbers in these diverse areas highlights their importance and demonstrates how they enrich mathematical understanding and contribute to various scientific and engineering fields.

There are several misconceptions surrounding square roots and irrational numbers, particularly regarding the square root of 7. Let's clarify some of these:

1. Belief: The square root of 7 can be expressed as a simple fraction.

Fact: The square root of 7 is an irrational number, meaning it cannot be represented as a fraction of two integers. Its decimal representation continues indefinitely without repeating.

2. Belief: Irrational numbers like √7 are impractical and rarely used in real-world applications.

Fact: Irrational numbers have significant applications in various fields such as physics, engineering, and computer science. They are crucial in precise calculations and modeling natural phenomena.

3. Belief: The classification of numbers into rational and irrational is arbitrary and unnecessary.

Fact: The distinction between rational and irrational numbers is fundamental in mathematics. It helps understand the structure of numbers and their behavior under operations like addition, subtraction, multiplication, and division.

4. Belief: The concept of irrational numbers is too complex for younger students to grasp.

Fact: While irrational numbers introduce a new idea beyond fractions and whole numbers, they can be introduced gradually with appropriate educational strategies. Understanding them enhances mathematical reasoning and problem-solving skills.

By addressing these misconceptions, we can appreciate the unique properties and importance of irrational numbers like the square root of 7 in mathematics and beyond.

Understanding irrational numbers like the square root of 7 unveils the richness of mathematical concepts beyond simple fractions and whole numbers. Embracing their beauty allows us to delve deeper into the intricacies of number theory and appreciate the elegance of mathematical abstraction.

While irrational numbers may initially seem perplexing, they play a vital role in shaping our understanding of the world around us, from the natural sciences to technology and art. Their infinite and non-repeating decimal expansions challenge us to explore new methods of calculation and problem-solving.

By acknowledging the significance of irrational numbers, we acknowledge the boundless creativity and ingenuity inherent in mathematics. Let us continue to celebrate and explore the profound beauty of these numbers that defy simple classification, enriching our mathematical journey and expanding our horizons.