Topic 7 square root of 3: Discover the fascinating world of 7 times the square root of 3. This article delves into its mathematical importance, real-world applications, and geometric interpretations, providing a comprehensive understanding of this intriguing expression.
Table of Content
- Understanding the Expression \(7\sqrt{3}\)
- Introduction to 7 Square Root of 3
- Mathematical Simplification
- Algebraic Applications
- Geometric Interpretations
- Trigonometric Context
- Physical and Engineering Applications
- Visualization and Graphical Representations
- Common Problems and Solutions
- FAQs
- YOUTUBE: Khám phá cách tính căn bậc hai của 7 một cách dễ dàng và chính xác. Video này sẽ giúp bạn hiểu rõ hơn về khái niệm này.
Understanding the Expression \(7\sqrt{3}\)
The expression \(7\sqrt{3}\) involves a constant multiplier (7) and the square root of 3. It frequently appears in various mathematical contexts such as simplifications, calculations, and problem-solving.
Mathematical Representation
The expression \(7\sqrt{3}\) can be represented and utilized in multiple forms:
- Exact Form: \(7\sqrt{3}\)
- Decimal Form: Approximately 12.124
Applications and Examples
This expression is often used in algebraic manipulations and geometry. Here are a few scenarios:
- Area Calculations: In problems involving equilateral triangles where the height can be expressed using \(7\sqrt{3}\).
- Trigonometric Functions: When solving for side lengths in trigonometry using sine and cosine functions.
- Simplifying Expressions: As part of simplifying complex algebraic expressions.
Simplification Example
To understand how \(7\sqrt{3}\) can be simplified or used in equations, consider the following example:
| Expression | \( \frac{7}{\sqrt{3}} \) |
| Step 1 | Multiply numerator and denominator by \(\sqrt{3}\) |
| Step 2 | \( \frac{7\sqrt{3}}{3} \) |
This process helps in rationalizing the denominator.
Visual Representation
Below is a geometric visualization where \(7\sqrt{3}\) might be used:
Conclusion
Understanding and applying the expression \(7\sqrt{3}\) is crucial in various mathematical problems. Its use in both exact and approximate forms allows for flexibility in solving equations and understanding geometrical properties.

READ MORE:
Introduction to 7 Square Root of 3
The expression \(7\sqrt{3}\) combines a constant multiplier (7) with the square root of 3, a fundamental irrational number in mathematics. This unique combination finds applications in various mathematical and real-world contexts, from algebra and geometry to physics and engineering.
Below, we explore the significance of \(7\sqrt{3}\) through several key points:
- Mathematical Properties: The value of \(\sqrt{3}\) is approximately 1.732, making \(7\sqrt{3}\) approximately 12.124.
- Geometric Interpretations: It appears in the dimensions of equilateral triangles and hexagons, contributing to the understanding of their properties.
- Algebraic Simplification: The expression can be simplified or transformed in various algebraic operations, such as rationalizing denominators.
- Trigonometric Relevance: It is related to certain trigonometric ratios and functions, particularly in the context of special triangles and angles.
- Physical Applications: In engineering, \(7\sqrt{3}\) can describe phenomena such as voltage calculations in three-phase power systems.
In the following sections, we will delve deeper into each of these aspects, providing a comprehensive understanding of the importance and applications of \(7\sqrt{3}\).
Mathematical Simplification
Simplifying the expression 7√3 involves understanding both its exact form and its decimal approximation. Let's break it down step by step:
Exact Form
The expression 7√3 is already in its simplest exact form. The number 7 is a coefficient, and √3 is an irrational number that cannot be simplified further. Therefore, 7√3 remains 7√3 in its exact form.
Decimal Approximation
To find the decimal approximation of 7√3, follow these steps:
- Calculate the square root of 3. The square root of 3 (√3) is approximately 1.732.
- Multiply this result by 7. So, 7 × 1.732 ≈ 12.124.
Thus, the decimal approximation of 7√3 is approximately 12.124.
Comparison Table
| Form | Value |
|---|---|
| Exact Form | 7√3 |
| Decimal Approximation | ≈ 12.124 |
Step-by-Step Example
Consider the following problem: Simplify 7√3 + 5√3.
- Step 1: Identify the common terms. Both terms contain √3.
- Step 2: Add the coefficients of √3. Here, 7 + 5 = 12.
- Step 3: Combine the terms. The simplified form is 12√3.
Therefore, 7√3 + 5√3 simplifies to 12√3.
Visualization
Graphical representations can help in understanding the value of 7√3. Below is a simple number line showing the approximate position of 7√3:

By understanding both the exact form and the decimal approximation of 7√3, we can appreciate its usage in various mathematical contexts.
Algebraic Applications
The expression \(7\sqrt{3}\) finds its utility in various algebraic contexts. Below are some applications and examples demonstrating its use:
Simplifying Expressions
In algebra, it's often necessary to simplify expressions involving radicals. The expression \(7\sqrt{3}\) can be used in various algebraic simplifications.
- For instance, to simplify the expression \(3(7\sqrt{3})\):
- Multiply the constants: \(3 \times 7 = 21\).
- Combine with the square root term: \(21\sqrt{3}\).
Solving Equations
Expressions involving \(7\sqrt{3}\) can also appear in equations. Consider the equation:
\(x + 7\sqrt{3} = 14\)
To solve for \(x\), isolate \(x\) on one side:
\(x = 14 - 7\sqrt{3}\)
This solution demonstrates how \(7\sqrt{3}\) can be manipulated within algebraic equations.
Quadratic Equations
Another application is in solving quadratic equations. For example, solve the quadratic equation:
\((x - 7\sqrt{3})^2 = 25\)
- Take the square root of both sides: \(x - 7\sqrt{3} = \pm 5\)
- Isolate \(x\):
- \(x = 7\sqrt{3} + 5\)
- \(x = 7\sqrt{3} - 5\)
Thus, the solutions are \(x = 7\sqrt{3} + 5\) and \(x = 7\sqrt{3} - 5\).
Applications in Word Problems
Word problems often require the use of square roots in their solutions. For example, consider a problem where the area of a square is given by \(49 \cdot 3\) square units, and we need to find the side length of the square.
- Calculate the area: \(49 \cdot 3 = 147\).
- Find the side length by taking the square root: \(\sqrt{147} = 7\sqrt{3}\).
The side length of the square is \(7\sqrt{3}\) units.
Polynomial Expressions
In polynomial expressions, \(7\sqrt{3}\) can be a coefficient or a term. For example, consider the polynomial:
\(P(x) = x^2 + 7\sqrt{3}x + 21\)
This polynomial can be factored or used in further algebraic operations where \(7\sqrt{3}\) plays a critical role.
These examples illustrate the versatility and importance of \(7\sqrt{3}\) in various algebraic applications, highlighting its utility in simplifying expressions, solving equations, and working through word problems.
Geometric Interpretations
The number 7√3 has several interesting geometric interpretations, especially in the context of right triangles and hexagons.
Here are a few key points where 7√3 plays a significant role in geometry:
- Right Triangles: In a right triangle, if one of the legs is 7 units long and the other leg is 7√3 units long, the hypotenuse can be calculated using the Pythagorean theorem:
- Let the legs be a = 7 and b = 7√3.
- The hypotenuse c is given by: \[ c = \sqrt{a^2 + b^2} = \sqrt{7^2 + (7\sqrt{3})^2} = \sqrt{49 + 147} = \sqrt{196} = 14 \]
- Equilateral Triangles: In an equilateral triangle with a side length of 7, the altitude (height) of the triangle can be found using the formula for the height of an equilateral triangle: \[ h = \frac{\sqrt{3}}{2} \times \text{side} = \frac{\sqrt{3}}{2} \times 7 = \frac{7\sqrt{3}}{2} \approx 6.06 \] However, if we consider a scaled version where each side is 7√3, the height becomes: \[ h = \frac{\sqrt{3}}{2} \times 7\sqrt{3} = \frac{21}{2} = 10.5 \]
- Hexagons: In a regular hexagon with side length \( s = 7 \), the distance between opposite sides (also known as the height of the hexagon) is: \[ \text{Height} = 2s\sqrt{3} = 14\sqrt{3} \] If we take a hexagon with side length \( s = 7\sqrt{3} \), the height is: \[ \text{Height} = 2(7\sqrt{3})\sqrt{3} = 42 \]
These interpretations show the versatility of 7√3 in various geometric contexts, highlighting its significance beyond mere numerical value.
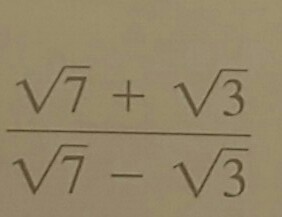
Trigonometric Context
The value \( 7\sqrt{3} \) frequently appears in various trigonometric contexts, especially within right triangles and unit circles. Here we explore its significance and applications in trigonometry.
1. Trigonometric Functions and Identities
Trigonometric functions such as sine, cosine, and tangent often involve the square root of 3. Key identities include:
- Sine and Cosine: \( \sin(30^\circ) = \frac{1}{2} \), \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \)
- Tangent: \( \tan(30^\circ) = \frac{1}{\sqrt{3}} \)
- Secant and Cosecant: \( \sec(30^\circ) = \frac{2}{\sqrt{3}} \), \( \csc(30^\circ) = 2 \)
2. Applications in Right Triangles
In a 30-60-90 triangle, the side lengths are in the ratio \( 1 : \sqrt{3} : 2 \). Therefore, if the shortest side (opposite the 30° angle) is 7 units:
- Opposite the 60° angle: \( 7\sqrt{3} \)
- Hypotenuse: \( 14 \)
3. Unit Circle and Angle Calculations
On the unit circle, angles that yield \( \sqrt{3} \) in their trigonometric calculations include:
- \( \sin(60^\circ) = \frac{\sqrt{3}}{2} \)
- \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \)
- \( \tan(60^\circ) = \sqrt{3} \)
4. Verifying Identities
Trigonometric identities can be verified using \( \sqrt{3} \). For example:
| Identity: | \( \tan^2(\theta) + 1 = \sec^2(\theta) \) |
| Example: | \( \tan^2(60^\circ) + 1 = \sec^2(60^\circ) \) |
| Simplified: | \( 3 + 1 = 4 \) |
5. Practical Examples
Consider the angle \( 60^\circ \) in real-world applications:
- Architecture: Calculating slopes and angles in roof designs.
- Physics: Resolving forces into components using trigonometric functions.
By understanding the role of \( 7\sqrt{3} \) in trigonometry, one can solve complex problems in mathematics, physics, and engineering more effectively.
Physical and Engineering Applications
The value \(7\sqrt{3}\) has significant applications in various fields of physics and engineering. Below, we explore some key areas where this mathematical expression plays a crucial role:
Power Engineering
In power engineering, the square root of 3 appears frequently, especially in the context of three-phase electrical systems. The voltage between any two phases in a balanced three-phase system is \( \sqrt{3} \) times the line-to-neutral voltage. Therefore, the voltage between phases is:
\[ V_{line-to-line} = \sqrt{3} \times V_{line-to-neutral} \]
For a system where the line-to-neutral voltage is 7 units, the line-to-line voltage becomes:
\[ V_{line-to-line} = 7\sqrt{3} \]
Mechanical Vibrations
In mechanical engineering, particularly in the study of vibrations, the factor \( \sqrt{3} \) is significant in analyzing systems' natural frequencies and resonance conditions. When scaling these systems, a factor like \(7\sqrt{3}\) can be used to adjust for certain dynamic properties.
Material Science and Stress Analysis
In material science and engineering, stress and strain relationships sometimes involve the square root of 3, particularly in the context of shear stress and principal stress calculations. For instance, in a plane stress condition, the maximum shear stress is given by:
\[ \tau_{max} = \frac{\sigma_1 - \sigma_2}{2} \]
Where \( \sigma_1 \) and \( \sigma_2 \) are principal stresses. If one of these principal stresses is scaled by a factor of \(7\sqrt{3}\), it significantly affects the resulting shear stress and material behavior.
Structural Engineering
In structural engineering, \(7\sqrt{3}\) can be encountered in the analysis and design of trusses and beams, where certain load conditions and support reactions are multiplied by this factor to maintain stability and safety under various loading conditions.
Fluid Dynamics
In fluid dynamics, particularly in the study of turbulent flow and boundary layers, factors involving the square root of 3 are used to simplify complex equations governing fluid motion. When scaling up these models for real-world applications, factors like \(7\sqrt{3}\) can be critical.
Signal Processing
In signal processing, especially in the analysis of waveforms and frequency modulation, the square root of 3 appears in calculations involving signal power and phase shifts. When these signals are amplified by a factor of 7, the resulting expressions often include \(7\sqrt{3}\).
- Three-phase systems in power engineering use the factor \(\sqrt{3}\) to relate line-to-line voltages to line-to-neutral voltages.
- In vibration analysis, scaling factors such as \(7\sqrt{3}\) adjust the natural frequencies of systems.
- Stress analysis in materials often involves principal stresses that are functions of \(\sqrt{3}\).
- Structural stability and load distribution in engineering rely on precise calculations involving this factor.
- Fluid dynamics and signal processing both use \(\sqrt{3}\) in modeling and scaling up equations for practical applications.
Visualization and Graphical Representations
Visualizing mathematical concepts helps in understanding and interpreting data more effectively. Here, we explore different methods to represent \(7\sqrt{3}\) graphically.
Graphing the Function:
Using tools like Desmos or GeoGebra, we can plot the function \(y = 7\sqrt{3}\) on a graph. This constant function will be represented as a horizontal line on the Cartesian plane, illustrating its value across all x-values.
Example of plotting \(y = 7\sqrt{3}\):
- Open a graphing calculator like or .
- Enter the equation \(y = 7\sqrt{3}\).
- Observe the horizontal line at approximately \(y = 12.12\) (since \(7\sqrt{3} \approx 12.12\)).
Geometric Representation:
To visualize \(7\sqrt{3}\) in a geometric context, consider its occurrence in right triangles. For instance, in a 30-60-90 triangle, the sides are in the ratio 1 : \(\sqrt{3}\) : 2. If the shorter leg is 7 units, the hypotenuse will be \(7 \times 2 = 14\) units, and the longer leg (opposite the 60° angle) will be \(7\sqrt{3}\) units.
Steps to visualize in a triangle:
- Draw a 30-60-90 triangle.
- Label the shorter leg as 7 units.
- Calculate the hypotenuse as 14 units.
- Label the longer leg as \(7\sqrt{3}\) units.
3D Representation:
Using a 3D graphing calculator like , you can plot \(7\sqrt{3}\) as a plane parallel to the x-y plane at \(z = 7\sqrt{3}\). This helps in understanding its value in three-dimensional space.
Example of plotting in 3D:
- Open the 3D graphing calculator.
- Enter the plane equation \(z = 7\sqrt{3}\).
- Observe the horizontal plane at \(z \approx 12.12\).
These visualizations provide a comprehensive understanding of \(7\sqrt{3}\) in different mathematical contexts, enhancing both intuitive and practical comprehension.
Common Problems and Solutions
Here, we address common problems involving 7 times the square root of 3 and provide detailed solutions to help you understand the concepts better.
Problem 1: Simplifying Expressions
How do you simplify the expression \(\frac{7}{\sqrt{3}}\)?
- Multiply the numerator and denominator by \(\sqrt{3}\) to rationalize the denominator:
- Result: \(\frac{7\sqrt{3}}{3}\)
\[
\frac{7}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{7\sqrt{3}}{3}
\]
Problem 2: Solving Equations
Solve the equation \(7\sqrt{3}x = 21\).
- Divide both sides by \(7\sqrt{3}\):
- Rationalize the denominator:
- Result: \(x = \sqrt{3}\)
\[
x = \frac{21}{7\sqrt{3}} = \frac{3}{\sqrt{3}}
\]
\[
x = \frac{3}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{3\sqrt{3}}{3} = \sqrt{3}
\]
Problem 3: Square Root Equations
Solve the equation \(\sqrt{7\sqrt{3} + x} = 4\).
- Square both sides to eliminate the square root:
- Isolate \(x\):
- Result: \(x = 16 - 7\sqrt{3}\)
\[
7\sqrt{3} + x = 16
\]
\[
x = 16 - 7\sqrt{3}
\]
Problem 4: Evaluating Expressions
Evaluate the expression \(7\sqrt{3} - 4\sqrt{3}\).
- Combine like terms:
- Result: \(3\sqrt{3}\)
\[
7\sqrt{3} - 4\sqrt{3} = (7 - 4)\sqrt{3} = 3\sqrt{3}
\]
Problem 5: Application in Geometry
Find the height of an equilateral triangle with side length \(14\).
- The height \(h\) of an equilateral triangle can be found using the formula \(h = \frac{\sqrt{3}}{2} \times \text{side length}\):
- Result: The height is \(7\sqrt{3}\)
\[
h = \frac{\sqrt{3}}{2} \times 14 = 7\sqrt{3}
\]

FAQs
Here are some frequently asked questions about 7 times the square root of 3:
-
What is the value of 7√3?
The value of \(7\sqrt{3}\) in decimal form is approximately 12.124. This is derived from the fact that \(\sqrt{3}\) is approximately 1.732, and multiplying it by 7 gives \(7 \times 1.732 \approx 12.124\).
-
Why is the square root of 3 an irrational number?
The square root of 3 is irrational because it cannot be expressed as a fraction of two integers. This is because 3 is a prime number and does not have any pair of equal factors, which means its square root does not terminate or repeat.
-
How is 7√3 used in algebraic expressions?
In algebra, \(7\sqrt{3}\) can be used in various expressions and equations. For example, it might be used to solve equations involving radicals or in simplifying expressions. One common problem is to rationalize a denominator, such as simplifying \(\frac{7}{\sqrt{3}}\), which involves multiplying by \(\frac{\sqrt{3}}{\sqrt{3}}\) to get \(\frac{7\sqrt{3}}{3}\).
-
Can 7√3 be simplified further?
No, \(7\sqrt{3}\) is already in its simplest form. It combines an integer with an irrational number, and there are no like terms to combine further.
-
What are some practical applications of 7√3?
\(7\sqrt{3}\) appears in various fields such as engineering and physics. For example, it might be used in calculations involving distances, forces, or other measurements where \(\sqrt{3}\) appears due to geometric relationships, especially in problems involving equilateral triangles and 30-60-90 triangles.
Khám phá cách tính căn bậc hai của 7 một cách dễ dàng và chính xác. Video này sẽ giúp bạn hiểu rõ hơn về khái niệm này.
Căn bậc hai của 7
READ MORE:
Hướng dẫn cách đơn giản hóa biểu thức (√3+√7)^2. Video này sẽ giúp bạn hiểu rõ hơn về cách làm bài toán với căn bậc hai của 3 và 7.
Q78 | Đơn giản hóa (√3+√7)^2 | căn bậc hai của 3 và 7

















