Topic 7 square root of 5: Discover the intriguing world of square roots with a focus on the expression "7 square root of 5." This guide will walk you through simplifying the expression, understanding its significance, and applying it in various mathematical contexts. Join us as we explore this fascinating topic and enhance your mathematical skills.
Table of Content
- Understanding the Expression: 7 Square Root of 5
- Introduction to Square Roots
- Understanding the Square Root of 5
- Methods to Simplify Square Roots
- Steps to Simplify 7/(Square Root of 5)
- Calculator Tools for Square Roots
- Properties and Characteristics of Square Roots
- Examples of Simplified Square Roots
- Common Problems and Solutions
- Practical Applications of Square Roots
- FAQs on Square Roots
- YOUTUBE:
Understanding the Expression: 7 Square Root of 5
The expression \( 7 \sqrt{5} \) combines a constant multiplier with a square root. Below is a detailed exploration of how to work with and understand this expression, along with related mathematical concepts.
Square Root Calculation
To understand the square root of a number, we look at a number which, when multiplied by itself, gives the original number. The square root of 5 is an irrational number approximately equal to:
\[ \sqrt{5} \approx 2.23607 \]
This means:
\[ 7 \sqrt{5} \approx 7 \times 2.23607 = 15.65249 \]
Rationalizing the Denominator
When simplifying expressions involving square roots, sometimes we need to rationalize the denominator. For example, simplifying \( \frac{7}{\sqrt{5}} \):
- Multiply by \( \frac{\sqrt{5}}{\sqrt{5}} \):
- The result is:
\[ \frac{7}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{7 \sqrt{5}}{5} \]
\[ \frac{7 \sqrt{5}}{5} \]
Simplifying Expressions
Consider simplifying expressions involving multiple square roots, such as:
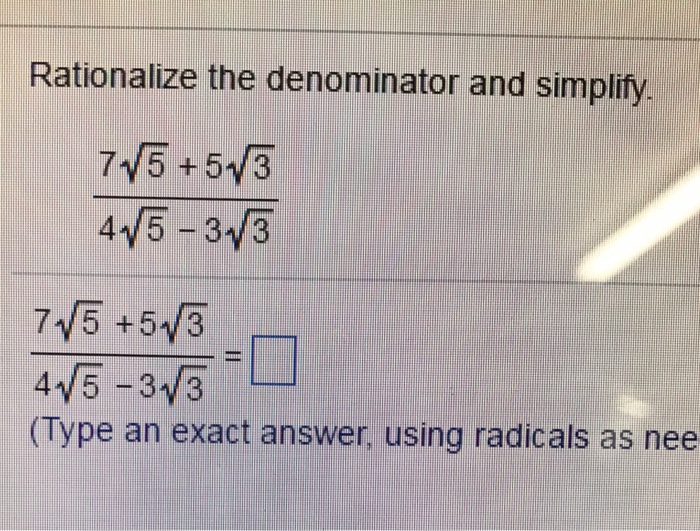
\[ \frac{\sqrt{7} + \sqrt{5}}{\sqrt{7} - \sqrt{5}} \]
- Multiply the numerator and the denominator by the conjugate of the denominator:
- Apply the FOIL method and simplify:
\[ \left( \frac{\sqrt{7} + \sqrt{5}}{\sqrt{7} - \sqrt{5}} \right) \times \left( \frac{\sqrt{7} + \sqrt{5}}{\sqrt{7} + \sqrt{5}} \right) \]
\[ \frac{(\sqrt{7} + \sqrt{5})^2}{(\sqrt{7})^2 - (\sqrt{5})^2} = \frac{7 + 2\sqrt{35} + 5}{7 - 5} = \frac{12 + 2\sqrt{35}}{2} = 6 + \sqrt{35} \]
Properties of Square Roots
Square roots have several important properties:
- For any positive number \( x \), \( \sqrt{x} \) is a positive number such that \( \sqrt{x} \times \sqrt{x} = x \).
- The square root function is continuous and increasing for all non-negative \( x \).
- Square roots of negative numbers are complex numbers, involving the imaginary unit \( i \) where \( i = \sqrt{-1} \).
Example Calculations
Here are some example calculations involving square roots:
| Expression | Approximate Value |
|---|---|
| \( \sqrt{5} \) | 2.23607 |
| \( 7 \sqrt{5} \) | 15.65249 |
| \( \frac{7}{\sqrt{5}} \) | 3.13049 |
Conclusion
The expression \( 7 \sqrt{5} \) and its related calculations demonstrate the application of square root properties and simplification techniques in algebra. Understanding these principles is crucial for working with more complex mathematical problems.
READ MORE:
Introduction to Square Roots
Square roots are fundamental in mathematics and are often encountered in various fields such as algebra, geometry, and calculus. A square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). The principal square root is the non-negative root, denoted as \( \sqrt{x} \). For example, \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \).
To understand square roots, it's important to know some key concepts and properties:
- Radical Sign: The symbol \( \sqrt{} \) used to denote the square root.
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25, which are squares of integers.
- Non-Perfect Squares: Numbers that do not result in an integer when their square root is taken, like 2, 3, and 5.
Square roots are used in various applications, such as solving quadratic equations, simplifying expressions, and in geometric calculations. Understanding how to simplify square roots is crucial:
- Factorization: Break down the number inside the square root into its prime factors. For instance, \( \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3} \).
- Combining Radicals: Use the property \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \) to simplify expressions. For example, \( \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5} \).
- Handling Fractions: Apply the rule \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). For example, \( \sqrt{\frac{30}{10}} = \frac{\sqrt{30}}{\sqrt{10}} = \sqrt{3} \).
Square roots are also essential in understanding irrational numbers, as many square roots result in non-repeating, non-terminating decimals. For instance, \( \sqrt{2} \approx 1.414 \), and it cannot be expressed exactly as a fraction.
By mastering these concepts, you can effectively work with square roots and apply them in various mathematical problems.
Understanding the Square Root of 5
The square root of 5, denoted as \(\sqrt{5}\), is an irrational number. This means it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating. The approximate value of \(\sqrt{5}\) is 2.23607.
Here are some important aspects to understand about the square root of 5:
- Irrational Number: As mentioned, \(\sqrt{5}\) is irrational, which means it is not a perfect square and its decimal form is non-terminating and non-repeating.
- Decimal Approximation: The value of \(\sqrt{5}\) to five decimal places is 2.23607, but it continues infinitely.
- Mathematical Representation: It can be represented using the radical symbol as
\(\sqrt{5}\)or in exponent form as5^{1/2}. - Geometric Interpretation: In geometry, \(\sqrt{5}\) can represent the length of the diagonal of a rectangle with sides of 1 and 2 units.
To gain a deeper understanding, let's consider how the square root of 5 appears in different mathematical contexts:
- Algebra: The equation \(x^2 = 5\) has two solutions, \(x = \sqrt{5}\) and \(x = -\sqrt{5}\). These solutions are called the principal square root and the negative square root, respectively.
- Geometry: In a right triangle where the legs are of lengths 1 and 2, the hypotenuse is \(\sqrt{5}\), derived from the Pythagorean theorem: \(c = \sqrt{a^2 + b^2}\).
- Calculus: The derivative of the function \(f(x) = \sqrt{x}\) at \(x = 5\) can be found using the power rule and is \(\frac{1}{2\sqrt{5}}\).
The square root of 5 is also important in various practical applications, such as in engineering and physics, where precise measurements and calculations are crucial. It appears in formulas involving quadratic equations, optimization problems, and even in the natural sciences.
By using a calculator, you can easily find the square root of 5 and apply it in various mathematical problems. For instance, to rationalize the denominator of a fraction involving \(\sqrt{5}\), follow these steps:
- Consider the fraction \(\frac{7}{\sqrt{5}}\).
- Multiply the numerator and the denominator by \(\sqrt{5}\) to eliminate the radical in the denominator.
- This gives \(\frac{7 \cdot \sqrt{5}}{\sqrt{5} \cdot \sqrt{5}} = \frac{7\sqrt{5}}{5}\).
Thus, \(\frac{7}{\sqrt{5}} = \frac{7\sqrt{5}}{5}\).
Methods to Simplify Square Roots
Simplifying square roots involves reducing the expression inside the radical to its simplest form. Here are some methods to simplify square roots:
Basic Steps to Simplify Square Roots
- Factor the number inside the square root into its prime factors.
- Pair the prime factors into groups of two.
- Move one factor from each pair outside the square root.
- Multiply the numbers outside the square root together.
- Multiply any remaining factors inside the square root.
Examples
- Example 1: Simplify √12
- Factor 12 into 4 and 3: √12 = √(4 × 3)
- Simplify using the property √(a × b) = √a × √b: √(4 × 3) = √4 × √3
- The square root of 4 is 2: √4 × √3 = 2√3
- Thus, √12 simplifies to 2√3.
- Example 2: Simplify √45
- Factor 45 into 9 and 5: √45 = √(9 × 5)
- Simplify: √(9 × 5) = √9 × √5
- The square root of 9 is 3: √9 × √5 = 3√5
- Thus, √45 simplifies to 3√5.
- Example 3: Simplify √18
- Factor 18 into 9 and 2: √18 = √(9 × 2)
- Simplify: √(9 × 2) = √9 × √2
- The square root of 9 is 3: √9 × √2 = 3√2
- Thus, √18 simplifies to 3√2.
Special Cases: Fractions
For fractions, the process is slightly different:
- Simplify the numerator and the denominator separately.
- Combine the results.
- Example: Simplify √(30 / 10)
- Combine the fraction under one square root: √(30 / 10)
- Simplify the fraction inside the root: √(3)
- Thus, √(30 / 10) simplifies to √3.
Additional Tips
- Use a calculator to verify your results if necessary.
- Remember that some square roots cannot be simplified and are left in their radical form, known as surds (e.g., √2, √3).
Understanding and practicing these methods will make simplifying square roots more intuitive over time.
Steps to Simplify 7/(Square Root of 5)
To simplify the expression \(\frac{7}{\sqrt{5}}\), follow these steps:
-
Identify the need to rationalize the denominator. The denominator in its current form, \(\sqrt{5}\), is irrational. To rationalize it, multiply both the numerator and the denominator by \(\sqrt{5}\).
\[
\frac{7}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{7\sqrt{5}}{5}
\] -
Combine the terms. Since \(\sqrt{5} \times \sqrt{5} = 5\), the expression simplifies to:
\[
\frac{7\sqrt{5}}{5}
\] -
Check for further simplification. In this case, the expression \(\frac{7\sqrt{5}}{5}\) is in its simplest form as there are no common factors between the numerator and the denominator.
Thus, the simplified form of \(\frac{7}{\sqrt{5}}\) is \(\frac{7\sqrt{5}}{5}\).

Calculator Tools for Square Roots
Understanding and simplifying square roots can be greatly aided by using online calculator tools. These tools are designed to perform a variety of functions, from finding the square root of a number to simplifying radical expressions. Here are some of the most useful tools and features:
- Basic Square Root Calculators: These calculators allow you to find the principal square root of any positive real number. For instance, using a calculator, you can easily find that the square root of 25 is 5.
- Perfect Square Detection: Some calculators can determine if a number is a perfect square and provide the root accordingly. For example, 16 is a perfect square because 42 = 16.
- Simplifying Radical Expressions: These tools can reduce square roots to their simplest radical form. For example, √50 can be simplified to 5√2.
- Handling Negative Numbers: Advanced calculators also provide solutions for the square roots of negative numbers, presenting results in terms of imaginary numbers (e.g., √-4 = 2i).
Examples of Online Square Root Calculators
- Calculator Soup: This calculator can find both the principal and negative roots of real numbers and will tell you if the number entered is a perfect square.
- Mathway: Offers step-by-step solutions and can handle both exact forms and decimal approximations of square roots.
- Math Warehouse: Provides both simplified radical forms and approximate decimal values for square roots.
Using these tools can make complex calculations easier and help you understand the underlying concepts of square roots and radical expressions.
Properties and Characteristics of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square roots of 25 are 5 and -5 because \(5^2 = 25\) and \((-5)^2 = 25\).
Basic Properties
- Every positive real number has two square roots: one positive (the principal square root) and one negative.
- The principal square root of a positive number \(x\) is denoted as \(\sqrt{x}\) and is always nonnegative.
- The square root of zero is zero: \(\sqrt{0} = 0\).
- Negative numbers do not have real square roots since the square of any real number is nonnegative.
Examples
| Number | Square Root |
|---|---|
| 16 | \(\pm4\) |
| 25 | \(\pm5\) |
| 0 | 0 |
| -9 | Not a real number |
Simplifying Square Roots
To simplify a square root, factor the radicand (the number inside the square root) into its prime factors. Pair the prime factors, and for each pair, take one factor out of the square root. For example:
- \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\)
- \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\)
Properties of Operations with Square Roots
- Product Property: \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- Quotient Property: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\), where \(b \ne 0\)
- Power Property: \(\sqrt{a^2} = |a|\)
For example, using the product property:
\(\sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5}\)
Irrational Numbers
The square root of a positive integer that is not a perfect square is always an irrational number. This means it cannot be expressed as a simple fraction and its decimal form is non-repeating and non-terminating.
For instance, \(\sqrt{2}\) is approximately 1.4142135... and goes on infinitely without repeating.
Graphical Representation
The graph of the square root function \(f(x) = \sqrt{x}\) shows that it is always increasing and only defined for nonnegative values of \(x\). The function is concave down, and the distance between perfect squares increases as \(x\) increases.
Examples of Simplified Square Roots
Understanding how to simplify square roots is crucial for solving various mathematical problems. Here, we present several examples to illustrate different methods of simplification.
Example 1: Simplifying the Square Root of 72
Steps:
- Factorize 72 into its prime factors: \(72 = 2^3 \times 3^2\)
- Separate the perfect squares: \(\sqrt{72} = \sqrt{(2^2 \times 3)^2 \times 2} = \sqrt{36 \times 2}\)
- Simplify: \(\sqrt{36} \times \sqrt{2} = 6\sqrt{2}\)
So, \(\sqrt{72} = 6\sqrt{2}\).
Example 2: Simplifying the Square Root of 108
Steps:
- Factorize 108 into its prime factors: \(108 = 2^2 \times 3^3\)
- Separate the perfect squares: \(\sqrt{108} = \sqrt{(2^2 \times 3^2) \times 3} = \sqrt{36 \times 3}\)
- Simplify: \(\sqrt{36} \times \sqrt{3} = 6\sqrt{3}\)
So, \(\sqrt{108} = 6\sqrt{3}\).
Example 3: Simplifying the Square Root of a Fraction
Example: \(\sqrt{\frac{28}{81}}\)
Steps:
- Apply the quotient property of square roots: \(\sqrt{\frac{28}{81}} = \frac{\sqrt{28}}{\sqrt{81}}\)
- Simplify the square root of the denominator: \(\frac{\sqrt{28}}{9}\)
- Further simplify the numerator if possible: \(\sqrt{28} = \sqrt{4 \times 7} = 2\sqrt{7}\)
- Combine the results: \(\frac{2\sqrt{7}}{9}\)
So, \(\sqrt{\frac{28}{81}} = \frac{2\sqrt{7}}{9}\).
Example 4: Simplifying Square Roots with Variables
Example: \(\sqrt{\frac{75x^5}{3x}}\)
Steps:
- Simplify the fraction inside the square root: \(\frac{75x^5}{3x} = 25x^4\)
- Apply the square root: \(\sqrt{25x^4} = \sqrt{25} \times \sqrt{x^4}\)
- Simplify: \(5x^2\)
So, \(\sqrt{\frac{75x^5}{3x}} = 5x^2\).
Example 5: Multiplication of Square Roots
Example: \(\sqrt{2} \times \sqrt{8}\)
Steps:
- Use the property of multiplication: \(\sqrt{a} \times \sqrt{b} = \sqrt{a \times b}\)
- Multiply under the radical: \(\sqrt{2 \times 8} = \sqrt{16}\)
- Simplify: \(\sqrt{16} = 4\)
So, \(\sqrt{2} \times \sqrt{8} = 4\).
Common Problems and Solutions
When dealing with the square root of 5, especially in expressions like \( \frac{7}{\sqrt{5}} \), several common problems can arise. Here, we address these problems with step-by-step solutions.
Problem 1: Rationalizing the Denominator
To simplify \( \frac{7}{\sqrt{5}} \), you need to rationalize the denominator. Follow these steps:
- Multiply both the numerator and the denominator by \( \sqrt{5} \) to remove the square root from the denominator.
- The expression becomes \( \frac{7 \sqrt{5}}{5} \).
- Simplify if possible. In this case, \( \frac{7 \sqrt{5}}{5} \) is already in its simplest form.
Therefore, \( \frac{7}{\sqrt{5}} = \frac{7 \sqrt{5}}{5} \).
Problem 2: Simplifying Complex Expressions
Consider an expression like \( \sqrt{20} + \sqrt{5} \). Here's how you simplify it:
- First, simplify \( \sqrt{20} \) by breaking it down into its prime factors: \( \sqrt{20} = \sqrt{4 \cdot 5} = \sqrt{4} \cdot \sqrt{5} = 2 \sqrt{5} \).
- Now, the expression is \( 2 \sqrt{5} + \sqrt{5} \).
- Combine like terms: \( 2 \sqrt{5} + \sqrt{5} = 3 \sqrt{5} \).
So, \( \sqrt{20} + \sqrt{5} = 3 \sqrt{5} \).
Problem 3: Solving Quadratic Equations Involving \( \sqrt{5} \)
Solve the equation \( x^2 - 5 = 0 \).
- Add 5 to both sides: \( x^2 = 5 \).
- Take the square root of both sides: \( x = \pm \sqrt{5} \).
Therefore, the solutions are \( x = \sqrt{5} \) and \( x = -\sqrt{5} \).
Problem 4: Simplifying Expressions with Multiple Square Roots
Simplify \( \sqrt{45} + \sqrt{5} \).
- First, simplify \( \sqrt{45} \) by breaking it down into its prime factors: \( \sqrt{45} = \sqrt{9 \cdot 5} = \sqrt{9} \cdot \sqrt{5} = 3 \sqrt{5} \).
- Now, the expression is \( 3 \sqrt{5} + \sqrt{5} \).
- Combine like terms: \( 3 \sqrt{5} + \sqrt{5} = 4 \sqrt{5} \).
So, \( \sqrt{45} + \sqrt{5} = 4 \sqrt{5} \).
Problem 5: Evaluating Expressions at Specific Values
Evaluate \( \sqrt{5x} \) for \( x = 4 \).
- Substitute \( x = 4 \) into the expression: \( \sqrt{5 \cdot 4} \).
- Simplify: \( \sqrt{20} \).
- Break down \( \sqrt{20} \) into its prime factors: \( \sqrt{20} = \sqrt{4 \cdot 5} = 2 \sqrt{5} \).
Therefore, \( \sqrt{5 \cdot 4} = 2 \sqrt{5} \).
By understanding these common problems and their solutions, you can confidently work with expressions involving the square root of 5.

Practical Applications of Square Roots
Square roots are used in various fields and practical applications that affect our daily lives. Here are some notable examples:
1. Architecture and Construction
Square roots play a crucial role in architectural design and construction. They are used to determine the dimensions and areas of different geometric shapes, ensuring accurate measurements for building structures. For instance, the Pythagorean theorem, which involves square roots, helps in calculating the diagonal distances in right-angled triangles, a common requirement in construction projects.
2. Engineering
In engineering, square roots are essential for analyzing forces, stress, and load distribution in structures. Engineers use square root calculations to determine the stability and safety of buildings, bridges, and other infrastructures. For example, the formula for stress involves the square root of force divided by the area.
3. Physics
Square roots are used in various physics equations and principles. They are crucial in calculating the period of a pendulum, analyzing wave functions, and determining distances in kinematic equations. For example, the period \(T\) of a simple pendulum is calculated using the formula \( T = 2\pi \sqrt{\frac{L}{g}} \), where \(L\) is the length of the pendulum and \(g\) is the acceleration due to gravity.
4. Finance
Square roots are also applied in finance, particularly in calculating compound interest and returns on investments. The square root formula helps in determining the annualized return over a given period. For example, the formula for annualized return \(R\) over a period of \(n\) years is \( R = \sqrt[n]{\frac{V_f}{V_i}} - 1 \), where \(V_f\) is the final value and \(V_i\) is the initial value.
5. Probability and Statistics
In probability and statistics, square roots are used to calculate standard deviations and variances, which measure the spread of data points in a dataset. The standard deviation is the square root of the variance, indicating how much the data deviates from the mean.
6. Computer Graphics
Square roots are integral in computer graphics for calculating distances between points, creating realistic animations, and rendering images. The distance formula in a 2D plane, \(D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\), uses square roots to determine the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\).
7. Everyday Measurements
Square roots are used in everyday measurements, such as determining the size of a room or a piece of land. For instance, if you know the area of a square room is 625 square feet, you can find the side length by calculating the square root of 625, which is 25 feet.
8. Artistic Design
In art and design, square roots, especially through the golden ratio, are used to create aesthetically pleasing compositions. The golden ratio, approximately 1.618, is often found by taking the square root of 5 and dividing it by 2, plus 1/2. This ratio is used in designing buildings, paintings, and even products.
These examples demonstrate the wide-ranging applications of square roots in various fields, highlighting their importance in both theoretical and practical contexts.
FAQs on Square Roots
Here are some common questions and detailed answers regarding square roots:
-
What is a square root?
A square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). It is denoted as \( \sqrt{x} \). For example, \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \).
-
How do you simplify the square root of a number?
To simplify a square root, factor the number into its prime factors and pair the common factors. For example, to simplify \( \sqrt{72} \):
- Prime factorize 72: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
- Pair the factors: \( (2 \times 2) \) and \( (3 \times 3) \)
- Take one factor from each pair: \( 2 \times 3 = 6 \)
- Simplified form: \( \sqrt{72} = 6\sqrt{2} \)
-
What is the square root of 5?The square root of 5 is an irrational number, approximately equal to \( 2.236 \). It cannot be expressed as a simple fraction.
-
How do you rationalize the denominator?
To rationalize the denominator involving a square root, multiply the numerator and the denominator by the square root found in the denominator. For example, to rationalize \( \frac{7}{\sqrt{5}} \):
- Multiply by \( \frac{\sqrt{5}}{\sqrt{5}} \): \( \frac{7 \times \sqrt{5}}{\sqrt{5} \times \sqrt{5}} \)
- Simplify: \( \frac{7\sqrt{5}}{5} \)
-
What are some applications of square roots?Square roots have various applications in different fields:
- In geometry, to find the side length of a square given its area.
- In physics, to calculate quantities like RMS (root mean square) values.
- In statistics, to compute standard deviations.
- In finance, to determine compound interest rates over time.
-
How do you solve quadratic equations using square roots?To solve a quadratic equation of the form \( ax^2 + bx + c = 0 \) using square roots:
- Isolate the \( x^2 \) term.
- Take the square root of both sides of the equation.
- Don't forget the ± sign, as both positive and negative roots are possible.
For example, for \( x^2 = 25 \):
- Take the square root: \( x = \pm \sqrt{25} \)
- Simplify: \( x = \pm 5 \)
Thủ Thuật Toán Học Căn Bậc Hai
READ MORE:
Cách ước lượng căn bậc hai của một số.
How to Approximate Square Root of a Number | Hướng dẫn ước lượng căn bậc hai của một số











