Topic 7 square root: The square root of 7 is a captivating mathematical concept that finds applications in various fields. From its calculation to its significance in geometry, algebra, and beyond, exploring the square root of 7 opens up a world of intriguing mathematical wonders. Join us as we delve into its properties, applications, and much more.
Table of Content
- Square Root of 7
- Introduction to Square Roots
- What is the Square Root of 7?
- Mathematical Representation of the Square Root of 7
- Calculating the Square Root of 7
- Square Root of 7 in Decimal Form
- Methods to Approximate the Square Root of 7
- Historical Context of Square Roots
- Applications of the Square Root of 7
- Square Root of 7 in Geometry
- Square Root of 7 in Algebra
- Square Root of 7 in Trigonometry
- Visualizing the Square Root of 7
- Square Root Properties and Rules
- Common Mistakes When Working with Square Roots
- Fun Facts About the Square Root of 7
- Conclusion
- YOUTUBE: Khám phá căn bậc hai của 7 trong video này để hiểu rõ hơn về tính chất và ứng dụng của số vô tỷ này trong toán học.
Square Root of 7
The square root of 7 is a mathematical constant that can be expressed in various forms and approximations. Below, we explore different aspects of the square root of 7, including its value, properties, calculation methods, and applications.
Value and Notation
The square root of 7 is denoted as \( \sqrt{7} \) or \( 7^{1/2} \). The approximate value of \( \sqrt{7} \) is 2.6457513110645906, which is often rounded to 2.645.
Calculation Methods
- Using Long Division Method:
- Using Babylonian Method:
By using the long division method, we can find the value of \( \sqrt{7} \) step by step, ultimately approximating it to three decimal places as 2.645.
The Babylonian method (or Newton's method) for finding the square root involves iterative approximations. Starting with an initial guess, each iteration improves the accuracy of the approximation.
Properties of \( \sqrt{7} \)
- It is an irrational number because it cannot be expressed as a simple fraction.
- It lies between the perfect squares of 4 (2²) and 9 (3²).
- The principal square root of 7 is positive, but it also has a negative counterpart: \( \pm \sqrt{7} \).
Applications in Geometry
In geometry, \( \sqrt{7} \) can be used in various contexts, such as calculating the hypotenuse of a right-angled triangle with legs of lengths \( \sqrt{3} \) and 2, where the hypotenuse will be \( \sqrt{7} \) or approximately 2.645.
Table of n-th Roots of 7
| Index (n) | n-th Root | Value |
|---|---|---|
| 2 | Square Root of 7 | \( \pm 2.6457513111 \) |
| 3 | Cube Root of 7 | 1.9129311828 |
| 4 | Fourth Root of 7 | \( \pm 1.6265765617 \) |
FAQs
- What is the square root of 7? The square root of 7 is approximately 2.6457513111.
- Is the square root of 7 an irrational number? Yes, because it cannot be expressed as a ratio of two integers.
- What is the square root of -7? The square root of -7 is an imaginary number and can be written as \( \pm 2.645i \), where \( i \) is the imaginary unit (\( \sqrt{-1} \)).

READ MORE:
Introduction to Square Roots
Square roots are fundamental mathematical operations that determine a number which, when multiplied by itself, yields the original number. For instance, the square root of 9 is 3, because \( 3 \times 3 = 9 \). This operation is denoted by the radical symbol \( \sqrt{} \). The square root of a number \( x \) is represented as \( \sqrt{x} \).
Here are some key points to understand about square roots:
- Definition: A square root of a number \( x \) is a value \( y \) such that \( y^2 = x \).
- Principal Square Root: The non-negative square root of a number is called its principal square root.
- Notation: The principal square root of \( x \) is written as \( \sqrt{x} \).
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are integers (1, 2, 3, 4, and 5, respectively).
Square roots have various properties and rules that make them useful in different areas of mathematics:
- Product Property: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \)
- Quotient Property: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
- Square of a Square Root: \( (\sqrt{a})^2 = a \)
To calculate the square root of a non-perfect square, various methods can be used, such as estimation, prime factorization, and using a calculator for more precise results.
| Number | Square Root |
| 1 | \( \sqrt{1} = 1 \) |
| 4 | \( \sqrt{4} = 2 \) |
| 9 | \( \sqrt{9} = 3 \) |
| 16 | \( \sqrt{16} = 4 \) |
| 25 | \( \sqrt{25} = 5 \) |
Understanding square roots is essential for advancing in more complex areas of mathematics, including algebra, geometry, and calculus. They are also widely used in real-world applications such as physics, engineering, and computer science.
What is the Square Root of 7?
The square root of 7, denoted as \( \sqrt{7} \), is a value that, when multiplied by itself, yields 7. Mathematically, it can be expressed as:
\[ \sqrt{7} \approx 2.6457513110645906 \]
This value is irrational, meaning it cannot be expressed as a simple fraction and its decimal representation goes on indefinitely without repeating.
Mathematical Representation
The square root of 7 can be represented in various forms:
- Decimal Form: \( 2.6457513110645906 \)
- Exponential Form: \( 7^{1/2} \) or \( 7^{0.5} \)
- Radical Form: \( \sqrt{7} \)
Why is the Square Root of 7 Irrational?
The square root of 7 is classified as an irrational number. Rational numbers can be expressed as a fraction of two integers, where the denominator is not zero. Examples include \( \frac{1}{2} \), -3, and 5. However, irrational numbers cannot be written as such simple fractions. Their decimal representations are non-repeating and non-terminating. The decimal form of \( \sqrt{7} \) continues indefinitely without settling into a repeating pattern, confirming its irrational nature.
Understanding through Geometry, Algebra, and Calculus
The square root of 7 is important in various branches of mathematics:
- In geometry, it helps determine side lengths of squares and other shapes.
- In algebra, it is used to solve quadratic equations and other polynomial equations.
- In calculus, it appears in various integrals and limits.
Methods to Calculate the Square Root of 7
Several methods can be used to calculate \( \sqrt{7} \):
- Long Division Method: This method involves dividing and averaging to achieve an accurate value. It is a step-by-step manual process that provides a precise value up to many decimal places.
- Estimation and Approximation: Understanding that \( \sqrt{7} \) lies between \( \sqrt{4} \) (which is 2) and \( \sqrt{9} \) (which is 3), we can estimate it to be closer to 2.6 and refine the guess through iteration.
- Number Line Method: Using a visual representation on a number line, we can understand the position of \( \sqrt{7} \) between 2 and 3 and approximate its value.
Mathematical Representation of the Square Root of 7
The square root of 7 is represented mathematically as \( \sqrt{7} \). This symbol indicates the principal (positive) square root of the number 7.
- Radical Form: The simplest way to denote the square root of 7 is by using the radical symbol: \( \sqrt{7} \).
- Exponent Form: It can also be expressed using exponents as \( 7^{1/2} \).
When dealing with square roots, it's essential to understand the properties and rules associated with them:
- Non-negative Values: The principal square root is always non-negative. Therefore, \( \sqrt{7} \) is positive.
- Product Property: For any positive numbers \(a\) and \(b\), \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \). For example, \( \sqrt{7 \cdot 2} = \sqrt{14} = \sqrt{7} \cdot \sqrt{2} \).
- Quotient Property: For any positive numbers \(a\) and \(b\), \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). For example, \( \sqrt{\frac{7}{2}} = \frac{\sqrt{7}}{\sqrt{2}} \).
To provide a more visual representation, we can consider a right triangle where one side is of length \( \sqrt{7} \) units. This is particularly useful in geometry and trigonometry for visualizing the square root values.
| Representation | Form |
|---|---|
| Radical | \( \sqrt{7} \) |
| Exponent | \( 7^{1/2} \) |
By understanding these mathematical representations, one can apply the square root of 7 in various mathematical contexts, including solving equations, geometry, and beyond.
Calculating the Square Root of 7
Calculating the square root of a number like 7 can be approached using various methods. Here, we outline some common techniques:
- Estimation and Refinement:
- Start with an initial guess. For example, since \(2^2 = 4\) and \(3^2 = 9\), we know that \( \sqrt{7} \) is between 2 and 3.
- Refine the guess by averaging:
If our first guess is 2.5, we calculate \(\frac{7}{2.5} = 2.8\).
Next, average 2.5 and 2.8 to get a better approximation: \(\frac{2.5 + 2.8}{2} = 2.65\).
- Repeat the process to get closer approximations. For instance, using 2.65, we calculate \(\frac{7}{2.65} \approx 2.6415\). Averaging 2.65 and 2.6415 gives us \(\approx 2.64575\).
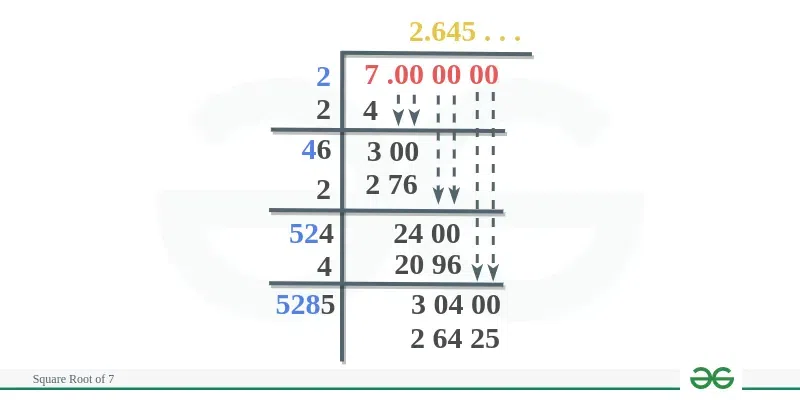
- Long Division Method:
- Pair the digits of the number starting from the decimal point. For 7, consider it as 7.000000.
- Find the largest number whose square is less than or equal to 7. This is 2 (since \(2^2 = 4\) and \(3^2 = 9\)). Write 2 as the first digit of the quotient.
- Subtract \(2^2 = 4\) from 7 to get a remainder of 3. Bring down a pair of zeros to make it 300.
- Double the quotient (2) to get 4, and determine the next digit (x) such that \(4x \cdot x \leq 300\). The closest is 7 (since \(47 \cdot 7 = 329\) and \(46 \cdot 6 = 276\)). Write 6 next to 4.
- Continue the process to refine the quotient.
- Using a Calculator:
The simplest way to find the square root of 7 is to use a calculator. Enter the number 7 and press the square root (√) button. The calculator will display an approximation, typically 2.6457513110645906.
Each method has its own merits, with estimation providing an intuitive understanding, the long division method offering a systematic approach, and calculators giving quick and accurate results.

Square Root of 7 in Decimal Form
The square root of 7, denoted as \( \sqrt{7} \), is an irrational number. This means it cannot be expressed as a simple fraction and its decimal representation is non-repeating and non-terminating.
In decimal form, the square root of 7 is approximately:
\( \sqrt{7} \approx 2.6457513110645906 \)
To provide a more detailed representation, the first few decimal places of \( \sqrt{7} \) are:
- 2.6457513110645906
- 2.645751311064591
- 2.6457513110645912
These values show the precision that can be achieved, but the decimal expansion continues indefinitely without repeating.
| Notation | Representation |
|---|---|
| Exponential Form | \( 7^{\frac{1}{2}} \) or \( 7^{0.5} \) |
| Radical Form | \( \sqrt{7} \) |
Understanding the decimal form of the square root of 7 is crucial for various applications in geometry, algebra, and calculus, where precise calculations are often required.
Methods to Approximate the Square Root of 7
Approximating the square root of 7 involves several methods that can be used to get as close as possible to the actual value. Here are some common methods:
- Long Division Method:
- Write the number 7 in decimal form (i.e., 7.0000).
- Divide 7 by a number such that the product of that number with itself is less than or equal to 7. For example, 2×2 = 4.
- Subtract the result (4) from 7, giving a remainder of 3.
- Double the quotient (2) to get 4 and use 40 as the new divisor.
- Bring down two zeros to get 300 as the new dividend.
- Find a number that, when added to 40 and multiplied by itself, is less than or equal to 300. Here, 46×6 = 276.
- Subtract 276 from 300 to get a remainder of 24 and a quotient of 2.6.
- Repeat the process to get a more precise value, up to 3 decimal places.
- Newton's Method:
- Start with an initial guess, say 2.5.
- Apply the iteration formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{7}{x_n} \right) \).
- Continue the iterations until the value stabilizes. For example, after a few iterations: \( x_1 = 2.65 \), \( x_2 = 2.6458 \), etc.
- Using a Calculator:
Simply enter the number 7 and use the square root function to get an approximate value, which is 2.64575131. For practical purposes, this is often rounded to 2.646.
These methods provide a way to approximate the square root of 7, each with its own level of accuracy and complexity.
Historical Context of Square Roots
The concept of square roots has a rich history, dating back to ancient civilizations. The Babylonians, around 1800 BCE, developed methods to approximate square roots. Their techniques were surprisingly accurate and involved iterative methods similar to those used today.
In ancient Greece, the Pythagoreans were fascinated by the properties of numbers, including square roots. They discovered that the square root of 2 is irrational, which was a significant mathematical milestone. This discovery led to the development of the theory of irrational numbers.
Chinese mathematicians also made significant contributions. The mathematician Liu Hui in the 3rd century CE provided a method to approximate square roots by an iterative process. This method was later refined by the mathematician Zu Chongzhi.
During the medieval Islamic period, scholars translated and expanded upon the works of the Greeks and Indians. Al-Khwarizmi, a prominent mathematician, included methods for finding square roots in his works, which were later translated into Latin and influenced European mathematics.
In the Renaissance, European mathematicians further developed methods for calculating square roots. The advent of calculus in the 17th century provided new tools for understanding and approximating square roots with greater precision.
Today, square roots are a fundamental concept in mathematics, used in various fields such as geometry, algebra, and trigonometry. The development of efficient algorithms for computing square roots continues to be an area of mathematical research.
Applications of the Square Root of 7
The square root of 7, approximately 2.6457513110645906, has several important applications in various fields of mathematics and science. Here are some notable examples:
- Geometry:
In geometry, the square root of 7 is used to determine the lengths of sides in certain right-angled triangles and other geometric shapes. For instance, in a right-angled triangle where the lengths of the legs are both \(\sqrt{7}\), the hypotenuse can be calculated using the Pythagorean theorem:
\[ c = \sqrt{(\sqrt{7})^2 + (\sqrt{7})^2} = \sqrt{7 + 7} = \sqrt{14} \]
- Algebra:
In algebra, the square root of 7 appears in various quadratic equations. For example, solving the equation:
\[ x^2 - 7 = 0 \]
leads to solutions involving \(\sqrt{7}\):
\[ x = \pm \sqrt{7} \]
- Trigonometry:
In trigonometry, the square root of 7 can be used to find the sides of triangles and in various trigonometric identities. For example, in a triangle with sides 1, \(\sqrt{7}\), and \(\sqrt{8}\), the cosine of the angle opposite the side of length \(\sqrt{8}\) can be found using the cosine rule:
\[ \cos(C) = \frac{1^2 + (\sqrt{7})^2 - (\sqrt{8})^2}{2 \cdot 1 \cdot \sqrt{7}} = \frac{1 + 7 - 8}{2 \sqrt{7}} = 0 \]
- Physics:
In physics, the square root of 7 can appear in formulas and calculations involving wave frequencies, energy levels, and other phenomena. For example, the energy levels of an electron in a hydrogen atom can involve roots of non-integer numbers.
- Engineering:
Engineers may encounter the square root of 7 in calculations involving signal processing, structural analysis, and material science. For example, when analyzing the resonance frequencies of a system, \(\sqrt{7}\) might appear in the equations describing the system's behavior.
- Computer Science:
In computer algorithms, particularly those involving numerical methods and optimizations, the square root of 7 can be used in iterative methods for solving equations, such as the Newton-Raphson method for finding roots of real-valued functions.

Square Root of 7 in Geometry
The square root of 7 has several interesting applications and constructions in geometry. One of the fundamental ways to understand and visualize the square root of 7 is through geometric constructions using a compass and straightedge.
Here is a step-by-step method to construct the square root of 7:
- Start with a line segment \(AB\) of length 1 unit.
- Draw a perpendicular line \(BC\) from point \(B\) such that \(BC\) is also 1 unit long. Now, \(AC\) forms the hypotenuse of the right triangle \(ABC\), and by the Pythagorean theorem, \(AC = \sqrt{2}\).
- Next, extend \(AC\) to a new point \(D\) such that \(CD\) is 1 unit. Now, \(AD\) is the hypotenuse of the right triangle \(ACD\), giving \(AD = \sqrt{3}\).
- Continue this process by drawing a perpendicular line \(DE\) from \(D\) of 1 unit length. \(AE\) becomes the hypotenuse of the right triangle \(ADE\), resulting in \(AE = \sqrt{4} = 2\).
- To find \(\sqrt{5}\), extend \(AE\) to a new point \(F\) such that \(EF\) is 1 unit. \(AF\) is now the hypotenuse of the right triangle \(AEF\), yielding \(AF = \sqrt{5}\).
- Following the same method, construct \(\sqrt{6}\) by extending \(AF\) to \(G\) with \(FG\) of 1 unit. \(AG\) then becomes the hypotenuse of the right triangle \(AFG\), resulting in \(AG = \sqrt{6}\).
- Finally, extend \(AG\) to \(H\) such that \(GH\) is 1 unit. \(AH\) will be the hypotenuse of the right triangle \(AGH\), and \(AH = \sqrt{7}\).
This method of constructing successive square roots geometrically illustrates how \(\sqrt{7}\) can be visualized as a sequence of right triangles.
Additionally, the square root of 7 can be involved in more complex geometric problems. For example, the diagonal of a rectangle with side lengths 1 and \(\sqrt{6}\) will be \(\sqrt{7}\), due to the Pythagorean theorem. This can be visualized in the following table:
| Rectangle Side Lengths | Diagonal |
|---|---|
| 1, \(\sqrt{6}\) | \(\sqrt{7}\) |
The square root of 7 also appears in more advanced geometric contexts, such as in the minimal enclosing rectangle of an equilateral triangle with edge length 2. The diagonal of this rectangle is \(\sqrt{7}\).
These geometric constructions and applications demonstrate the versatility and utility of the square root of 7 in various geometric problems and visualizations.
Square Root of 7 in Algebra
The square root of 7 in algebra is represented symbolically as \( \sqrt{7} \). It is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation goes on infinitely without repeating.
To work with \( \sqrt{7} \) algebraically, it's important to understand its properties:
- Multiplication and Division: \( \sqrt{7} \times \sqrt{7} = 7 \) and \( \frac{\sqrt{7}}{\sqrt{7}} = 1 \).
- Exponentiation: \( (\sqrt{7})^2 = 7 \) and \( (\sqrt{7})^3 = 7\sqrt{7} \).
- Algebraic Manipulation: \( \sqrt{7} \) can be added or subtracted with other terms as required in algebraic equations.
When solving algebraic equations involving \( \sqrt{7} \), it's common to simplify expressions using the properties of radicals and the distributive property.
Square Root of 7 in Trigonometry
In trigonometry, the square root of 7, denoted as \( \sqrt{7} \), appears in various contexts:
- Unit Circle: \( \sqrt{7} \) is a crucial value when calculating trigonometric functions such as sine, cosine, and tangent for specific angles.
- Angle Measurement: \( \sqrt{7} \) often arises in trigonometric identities and calculations involving angles that result in \( \sqrt{7} \) as a side length or ratio.
- Trigonometric Identities: \( \sqrt{7} \) can be part of trigonometric identities and equations, influencing the values of sine, cosine, and tangent depending on the context of the triangle or unit circle.
Understanding \( \sqrt{7} \) in trigonometry helps in solving problems related to triangles, circular functions, and applications in fields such as physics, engineering, and astronomy.
Visualizing the Square Root of 7
Understanding the square root of 7 can be greatly enhanced through visualization. Here, we will explore different ways to visualize this mathematical concept.
Graphical Representation
One of the simplest ways to visualize the square root of 7 is on a number line. Marking points between integers can help understand the approximate value of the square root of 7.
Consider the number line below:
- 2.6 is just below the square root of 7
- 2.7 is just above the square root of 7
The square root of 7 is approximately 2.6457513110645906, lying between 2.6 and 2.7.
Geometric Representation
Another way to visualize the square root of 7 is by using geometric shapes.
Let's use a square for this purpose:
- Draw a square with an area of 7 square units.
- The side length of this square will be the square root of 7.
This geometric representation helps to visually comprehend the value as the side length of the square.
Pythagorean Theorem
The Pythagorean theorem can also be utilized to visualize the square root of 7. Consider a right-angled triangle where one side is of length 1 unit and the other side is of length √6 units:
- The length of the hypotenuse will be √(1^2 + (√6)^2).
- This simplifies to √(1 + 6) = √7.
Thus, the hypotenuse of this triangle represents the square root of 7.
Approximation Using Circles
Another effective method is through the use of circles:
- Draw a circle with a radius of √7 units.
- The diameter of this circle would be 2√7 units.
This visual approximation can help in understanding the square root in a more concrete manner.
Interactive Tools
There are also various online tools and calculators available to visualize and approximate the square root of 7. These tools often include interactive graphs and step-by-step calculations to aid comprehension.
By using these visual methods, one can gain a deeper understanding of the square root of 7 and its applications in different mathematical contexts.

Square Root Properties and Rules
The square root function has several important properties and rules that are essential for understanding its behavior and applications. Here are some key properties and rules:
- Non-negative Property: The square root of a non-negative number is always non-negative. If \(x \geq 0\), then \(\sqrt{x} \geq 0\).
- Product Rule: The square root of a product is equal to the product of the square roots of the factors. Mathematically, \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\).
- Quotient Rule: The square root of a quotient is equal to the quotient of the square roots. Mathematically, \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) for \(b \neq 0\).
- Power Rule: The square root of a number can be expressed as a power. Specifically, \(\sqrt{x} = x^{1/2}\).
- Even and Odd Numbers:
- The square root of an even number is always even.
- The square root of an odd number is always odd.
- Square of Square Roots: The square of the square root of a number is the number itself. Mathematically, \((\sqrt{x})^2 = x\).
- Negative Numbers: The square root of a negative number is not a real number but an imaginary number. For example, \(\sqrt{-7} = \sqrt{7}i\) where \(i = \sqrt{-1}\).
- Sum of Odd Numbers: The square of a natural number \(n\) is equal to the sum of the first \(n\) odd numbers. For example, \(5^2 = 1 + 3 + 5 + 7 + 9\).
- Rationalizing the Denominator: To simplify expressions with square roots in the denominator, multiply the numerator and denominator by the conjugate or the appropriate radical form to eliminate the square root from the denominator.
Understanding these properties and rules is crucial for solving problems involving square roots and for simplifying expressions in algebra and beyond.
Common Mistakes When Working with Square Roots
Working with square roots can be challenging, and it's easy to make mistakes. Here are some common errors and tips on how to avoid them:
-
Mistake: Misinterpreting the Principal Square Root
Incorrect: \( \sqrt{25} = \pm 5 \)
Correct: \( \sqrt{25} = 5 \)
The square root symbol \( \sqrt{} \) represents only the principal (positive) square root. To indicate both positive and negative roots, write \( \pm 5 \).
-
Mistake: Incorrectly Simplifying Square Roots of Sums
Incorrect: \( \sqrt{9 + 16} = \sqrt{9} + \sqrt{16} \)
Correct: \( \sqrt{9 + 16} \ne \sqrt{9} + \sqrt{16} \)
The correct simplification is \( \sqrt{25} = 5 \).
-
Mistake: Misunderstanding Square Root of a Product
Incorrect: \( \sqrt{x^2 + y^2} = x + y \)
Correct: \( \sqrt{x^2 + y^2} \ne x + y \)
Example: \( \sqrt{12^2 + 5^2} = \sqrt{144 + 25} = \sqrt{169} = 13 \ne 12 + 5 \).
-
Mistake: Adding Square Roots Incorrectly
Incorrect: \( 3\sqrt{5} + 2\sqrt{5} = 6\sqrt{5} \)
Correct: \( 3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5} \)
You can add square roots only if the radicands are the same.
-
Mistake: Incorrectly Squaring Fractions and Decimals
Incorrect: \( 0.2^2 = 0.4 \)
Correct: \( 0.2^2 = 0.04 \)
Example: \( 0.2 \times 0.2 = 0.04 \).
-
Mistake: Neglecting Parentheses in Expressions
Incorrect: \( (4a)^2 = 4a^2 \)
Correct: \( (4a)^2 = 16a^2 \)
Parentheses indicate that the entire expression inside should be squared.
-
Mistake: Incorrectly Squaring Negative Numbers
Incorrect: \( (-3)^2 = -9 \)
Correct: \( (-3)^2 = 9 \)
Squaring a negative number results in a positive value.
To avoid these mistakes, it's essential to understand the properties of square roots and practice regularly. This will help build a solid foundation and minimize errors.
Fun Facts About the Square Root of 7
- The square root of 7, approximately 2.64575, is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal form goes on forever without repeating.
- In ancient Indian texts like the "Shulba Sutra," written around 800 BC, there are references to methods of calculating square roots, highlighting the long history of mathematical exploration surrounding square roots.
- The square root of 7 can be calculated using various methods, including Newton's method, which is an iterative numerical technique that converges very quickly to the correct value.
- Digital cameras utilize square root calculations when processing images. They store the square root of pixel brightness values to efficiently manage the dynamic range and then square these values when displaying the images.
- The radical symbol (√) used to denote square roots was introduced by Christoph Rudolff in 1525, and the horizontal line (vinculum) above the numbers was added by René Descartes in 1637.
- Geometrically, the square root of 7 can be represented using the Pythagorean theorem. If you have a right triangle with sides of length √3 and √4, the hypotenuse will be √7.
- Square Root Day is celebrated on dates where both the day of the month and the month are the square root of the last two digits of the year, such as 4/4/16 (April 4, 2016).
- In 2015, Google's parent company, Alphabet, repurchased stock worth $5,099,019,513.59, which is the square root of 26 (the number of letters in the alphabet) times a billion.
Conclusion
The square root of 7, represented as \( \sqrt{7} \), is a fascinating and complex number that highlights the richness of mathematical concepts. As an irrational number, its decimal expansion is non-repeating and infinite, approximately 2.645751311. This property makes \( \sqrt{7} \) unique and distinguishes it from rational numbers, which can be expressed as simple fractions.
Understanding \( \sqrt{7} \) involves a variety of methods and mathematical tools. From manual techniques like the long division method to modern computational algorithms, calculating the square root of 7 offers valuable insights into both historical and contemporary mathematical practices. This number appears in various applications across geometry, algebra, and trigonometry, showcasing its versatility and importance.
Moreover, \( \sqrt{7} \) serves as a gateway to exploring broader mathematical concepts such as irrational numbers and their properties. It reminds us of the inherent complexity in the number system and the beauty found within mathematical exploration. Whether approximated visually or calculated precisely, the square root of 7 continues to intrigue and inspire mathematicians and students alike.
In conclusion, the square root of 7 is more than just a number; it is a symbol of the depth and intricacy of mathematics. Its study encourages a deeper appreciation of numerical relationships and the endless possibilities within the realm of mathematics.
Khám phá căn bậc hai của 7 trong video này để hiểu rõ hơn về tính chất và ứng dụng của số vô tỷ này trong toán học.
Căn Bậc Hai Của 7
READ MORE:
Tìm căn bậc hai của 7 với độ chính xác đến 3 chữ số thập phân
Tìm căn bậc hai của 7 đến 3 chữ số thập phân | Toán học cơ bản











