Topic square root of 1/20: The square root of 1/20 is a fascinating mathematical concept that has practical applications in various fields. This article explores how to calculate and simplify √(1/20), its decimal approximation, and its relevance in everyday problems. Join us as we delve into the steps and methods to understand this unique square root.
Table of Content
- Understanding the Square Root of 1/20
- Introduction to Square Roots
- Understanding the Square Root of Fractions
- Calculating the Square Root of 1/20
- Step-by-Step Simplification Process
- Decimal and Exact Form of Square Root of 1/20
- Visual Representation of Square Root of 1/20
- Mathematical Properties and Applications
- Common Mistakes and Misconceptions
- Practical Examples Using Square Root of 1/20
- Further Resources and Reading
- YOUTUBE: Video này giới thiệu cách tính hình vuông và căn vuông của các số từ 1 đến 20. Một tài nguyên hữu ích để nâng cao hiểu biết toán học của bạn.
Understanding the Square Root of 1/20
The square root of a fraction can be found by taking the square root of the numerator and the square root of the denominator separately.
Mathematical Representation
The square root of \( \frac{1}{20} \) can be expressed as:
This simplifies to:
Further simplifying, we get:
Decimal Representation
In decimal form, this is approximately:
Steps to Calculate Manually
- Rewrite the fraction under the square root as \( \frac{1}{20} \).
- Simplify using the property \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
- Calculate the square roots of the numerator and the denominator separately:
- \( \sqrt{1} = 1 \)
- \( \sqrt{20} \approx 4.472 \)
- Combine the results to get \( \frac{1}{\sqrt{20}} \).
- Simplify further to \( \frac{1}{2\sqrt{5}} \), if needed rationalize to \( \frac{\sqrt{5}}{10} \).
Applications
The square root of fractions like \( \frac{1}{20} \) are commonly used in mathematical computations involving proportions, physics equations, and statistical calculations.
Visual Representation
The image below shows the geometric interpretation of the square root of fractions:

Further Reading

READ MORE:
Introduction to Square Roots
Square roots are fundamental in mathematics and have applications in various fields, including geometry, physics, and engineering. A square root of a number \( x \) is a value that, when multiplied by itself, gives the original number \( x \). This operation is represented by the symbol \( \sqrt{} \).
For example, the square root of 25 is 5, because \( 5 \times 5 = 25 \). Square roots can be both positive and negative because \( (-5) \times (-5) \) also equals 25. However, in most contexts, the positive square root, also known as the principal square root, is considered.
In algebra, square roots are often simplified for ease of calculation. To simplify a square root, you factor the number under the root into its prime factors and extract pairs of identical factors. For instance:
- To simplify \( \sqrt{18} \), you factorize 18 into \( 2 \times 3 \times 3 \). Then, \( \sqrt{18} \) simplifies to \( 3\sqrt{2} \), as the pair of 3s come out of the root as a single 3.
- For fractions, like \( \sqrt{\frac{1}{20}} \), the process involves simplifying both the numerator and the denominator separately. Here, \( \sqrt{\frac{1}{20}} = \frac{\sqrt{1}}{\sqrt{20}} = \frac{1}{\sqrt{20}} \), which further simplifies to \( \frac{1}{2\sqrt{5}} \).
The general formula for the square root of a number \( x \) can be expressed using exponentiation as \( x^{1/2} \). This representation is especially useful when dealing with higher-order operations or when using calculators.
Square roots are crucial in solving quadratic equations and are often used in conjunction with other mathematical operations, such as addition, subtraction, multiplication, and division of roots. When dealing with such operations, it's important to simplify the roots where possible to make the calculations manageable.
Understanding the Square Root of Fractions
The concept of square roots extends seamlessly to fractions. To find the square root of a fraction, we apply the same principles used for whole numbers. If we consider a fraction \( \frac{a}{b} \), its square root can be expressed as \( \sqrt{\frac{a}{b}} \), which can be further simplified using the property \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
Let’s break down the process of finding the square root of \( \frac{1}{20} \):
- Rewrite the fraction under the square root: \( \sqrt{\frac{1}{20}} \).
- Separate the numerator and the denominator under their own square roots:
- Simplify each part individually:
- The square root of the numerator \( \sqrt{1} = 1 \).
- The square root of the denominator \( \sqrt{20} = \sqrt{4 \times 5} = 2 \sqrt{5} \), since 20 can be factored into \( 4 \times 5 \).
- Combine the simplified parts:
- Rationalize the denominator to make the expression simpler:
Multiply the numerator and the denominator by \( \sqrt{5} \):
Thus, the square root of \( \frac{1}{20} \) simplifies to \( \frac{\sqrt{5}}{10} \). This approach can be applied to any fractional number, allowing for easy computation and simplification of square roots.
Square roots of fractions appear frequently in various mathematical contexts, from solving equations to understanding proportions in geometry. Mastering this process equips you with a fundamental tool in both pure and applied mathematics.
Calculating the Square Root of 1/20
Calculating the square root of a fraction like \( \frac{1}{20} \) involves a straightforward method that applies the fundamental properties of square roots. Here’s a step-by-step guide to determine and simplify \( \sqrt{\frac{1}{20}} \).
-
Rewrite the Expression:
Begin by expressing the square root of the fraction as:
-
Simplify the Numerator and Denominator:
-
The square root of the numerator \( \sqrt{1} \) is 1, because any number squared to 1 is 1:
-
Simplify the square root of the denominator \( \sqrt{20} \) by factoring 20 into its prime components \( 4 \times 5 \):
-
The square root of the numerator \( \sqrt{1} \) is 1, because any number squared to 1 is 1:
-
Extract Square Roots of Perfect Squares:
Since 4 is a perfect square, it simplifies to 2:
Thus, the expression simplifies to:
-
Combine the Simplified Roots:
Place the simplified numerator and denominator back together:
-
Rationalize the Denominator:
To simplify further and remove the square root from the denominator, multiply both the numerator and the denominator by \( \sqrt{5} \):
-
Final Simplified Form:
The simplified and rationalized form of \( \sqrt{\frac{1}{20}} \) is:
Understanding the process of calculating the square root of fractions like \( \frac{1}{20} \) enhances your ability to solve complex mathematical problems and applies directly to real-world scenarios where precision and simplification are essential.
Step-by-Step Simplification Process
Simplifying the square root of a fraction, such as \( \frac{1}{20} \), involves breaking down the fraction into more manageable parts and applying basic principles of square roots. Follow these detailed steps to simplify \( \sqrt{\frac{1}{20}} \).
-
Express the Square Root as a Fraction:
Begin by writing the square root of the fraction in its standard form:
This uses the property that the square root of a fraction is the fraction of the square roots of the numerator and the denominator. -
Simplify the Numerator:
The numerator here is 1. The square root of 1 is straightforward:
-
Simplify the Denominator:
Next, factorize 20 to simplify its square root. 20 can be expressed as \( 4 \times 5 \):
Since \( 4 \) is a perfect square, it can be simplified to \( 2 \):
Thus,
-
Combine the Simplified Parts:
Now that both the numerator and the denominator are simplified, combine them:
This gives us the simplified form of \( \sqrt{\frac{1}{20}} \). -
Rationalize the Denominator:
To further simplify and rationalize the denominator, multiply both the numerator and the denominator by \( \sqrt{5} \):
-
Final Simplified Form:
The final rationalized form of \( \sqrt{\frac{1}{20}} \) is:
This is the simplest form of the square root of \( \frac{1}{20} \).
By following these steps, you can confidently simplify any fraction under a square root, making it easier to understand and work with in various mathematical contexts.
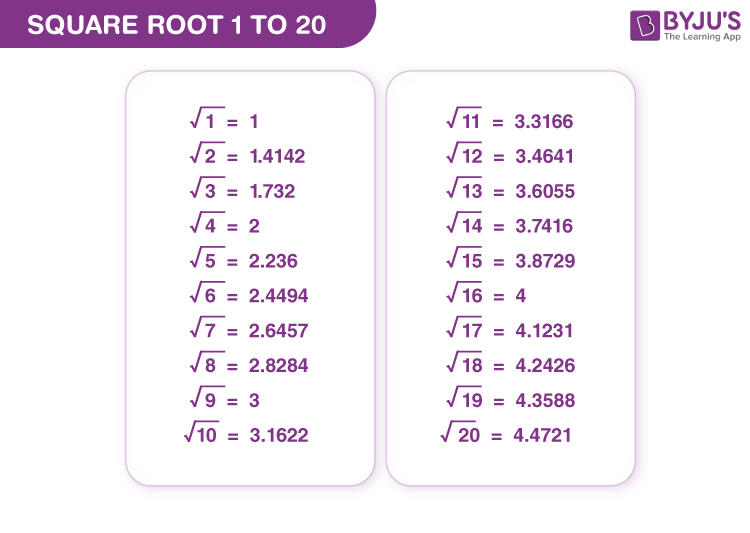
Decimal and Exact Form of Square Root of 1/20
Understanding both the exact form and the decimal approximation of square roots is essential for mathematical clarity and practical applications. Let’s explore the square root of \( \frac{1}{20} \) in both these forms.
Exact Form
To find the exact form of \( \sqrt{\frac{1}{20}} \), we use the property of square roots that allows us to separate the numerator and the denominator:
We know that the square root of 1 is simply 1, and we can simplify the square root of 20 by expressing it in terms of its factors:
This gives us:
To rationalize the denominator, multiply the numerator and the denominator by \( \sqrt{5} \):
Thus, the exact form of \( \sqrt{\frac{1}{20}} \) is:
Decimal Form
To find the decimal approximation, we first approximate the square root of 5:
Using this value, we divide by 10 to find:
Therefore, the decimal approximation of \( \sqrt{\frac{1}{20}} \) is approximately 0.2236.
Summary Table
| Form | Representation |
|---|---|
| Exact Form | |
| Decimal Form | 0.2236 |
By understanding both the exact and decimal forms, you can apply the square root of \( \frac{1}{20} \) effectively in various mathematical and real-world problems.
Visual Representation of Square Root of 1/20
Visualizing the square root of \( \frac{1}{20} \) can enhance understanding and provide insights into its properties. Here, we will explore graphical and geometric representations to illustrate the concept.
Graphical Representation
One way to visualize the square root of a fraction like \( \frac{1}{20} \) is by plotting its value on a number line or a graph. The decimal approximation of \( \sqrt{\frac{1}{20}} \) is approximately 0.2236. This can be shown on a number line between 0 and 1:
- On a number line, mark the points 0 and 1.
- Divide the segment between 0 and 1 into 10 equal parts to represent tenths.
- Since 0.2236 is slightly less than 0.25, mark a point just before 0.25.
On a graph, we can plot the function \( y = \sqrt{\frac{1}{20}} \) as a constant horizontal line at \( y \approx 0.2236 \):
For a more dynamic view, imagine plotting \( y = \sqrt{\frac{x}{20}} \) for various values of \( x \). This forms a curve that starts at \( y = 0 \) when \( x = 0 \) and increases gradually.
Geometric Representation
Geometrically, we can visualize \( \sqrt{\frac{1}{20}} \) using areas of squares. Consider a square with an area of \( \frac{1}{20} \) unit squares. The side length of this square represents \( \sqrt{\frac{1}{20}} \).
-
Start with a square unit grid and identify a smaller square whose area is \( \frac{1}{20} \). -
The side length of this smaller square is \( \sqrt{\frac{1}{20}} \), which is a fraction of the side length of a full unit square.
To better understand, imagine dividing a full unit square into 20 equal parts. Each part represents an area of \( \frac{1}{20} \). The side length of one of these parts is \( \sqrt{\frac{1}{20}} \).
Tabular Summary
For quick reference, here's a summary of the visual aspects of \( \sqrt{\frac{1}{20}} \):
| Representation | Description |
|---|---|
| Number Line | Located slightly before the 0.25 mark |
| Graph | A horizontal line at \( y \approx 0.2236 \) |
| Geometric Square | Side length of a square with area \( \frac{1}{20} \) |
Visualizing \( \sqrt{\frac{1}{20}} \) through these methods can help reinforce its conceptual understanding and practical application in various contexts.
Mathematical Properties and Applications
The square root of a fraction like 1/20 has several interesting mathematical properties and applications. Understanding these can enhance your comprehension of square roots and their practical uses.
Mathematical Properties
- Square Root of a Fraction: The square root of a fraction can be expressed as the square root of the numerator divided by the square root of the denominator. For example, \[ \sqrt{\frac{1}{20}} = \frac{\sqrt{1}}{\sqrt{20}} = \frac{1}{\sqrt{20}} = \frac{1}{2\sqrt{5}} = \frac{\sqrt{5}}{10} \]
- Irrational Number: The square root of 1/20 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation is non-terminating and non-repeating.
- Decimal Form: The approximate decimal form of \(\sqrt{1/20}\) is about 0.2236, which can be useful for quick calculations and estimations.
- Simplification: In its simplest radical form, \(\sqrt{1/20}\) simplifies to \(\frac{\sqrt{5}}{10}\), making it easier to work with in various mathematical contexts.
Applications
The square root of 1/20 has numerous practical applications in fields such as geometry, physics, and statistics. Here are a few examples:
- Geometry: In geometry, understanding the square root of fractions is essential when working with areas and lengths. For instance, if a shape's area is given as a fraction, knowing its square root helps in determining the side lengths.
- Physics: In physics, many formulas involve square roots of fractions, especially in wave mechanics and quantum physics. For example, calculating the root mean square speed of gas molecules often requires square root operations on fractions.
- Statistics: The square root of fractions frequently appears in statistics, particularly in standard deviation and variance calculations. These are fundamental in analyzing data spread and dispersion.
Understanding these properties and applications of \(\sqrt{1/20}\) enhances mathematical problem-solving skills and provides a foundation for more advanced mathematical concepts.
Common Mistakes and Misconceptions
Understanding and calculating the square root of a fraction like can often lead to errors and misconceptions. Here are some common pitfalls and how to avoid them:
- Misinterpreting the Square Root of a Fraction:
One common mistake is to forget that the square root of a fraction can be expressed as the fraction of the square roots. This means is equivalent to , which simplifies to . Forgetting this step can lead to incorrect simplifications.
- Overlooking the Simplification Process:
Another error is neglecting to simplify the radical expression. The square root of 20 can be simplified further since 20 is 4 times 5. Hence, becomes , so the expression simplifies to .
- Incorrect Decimal Conversion:
When converting the square root of a fraction to a decimal, ensure accuracy. The correct value for is approximately 0.2236. Using inaccurate values can affect the outcome of further calculations.
- Misapplying Properties of Square Roots:
Remember that properties like hold true. Misapplying these properties can lead to incorrect simplifications or interpretations of the expression.
- Ignoring the Rationalization of Denominators:
Sometimes, you may need to rationalize the denominator to simplify the expression. For example, can be rationalized by multiplying the numerator and the denominator by , resulting in . This step is crucial for obtaining the exact form of the expression.
By understanding these common mistakes and misconceptions, you can improve your accuracy and confidence in working with square roots of fractions.

Practical Examples Using Square Root of 1/20
The square root of 1/20 has various practical applications in mathematics and real-world scenarios. Below are some detailed examples:
1. Simplifying Expressions
When simplifying mathematical expressions, the square root of 1/20 can be used to simplify more complex terms. For instance:
- Simplify the expression: \( \frac{\sqrt{1/20}}{\sqrt{5}} \)
- First, simplify the fraction inside the square root: \[ \frac{1}{20} = \frac{1}{4 \times 5} \]
- Apply the property of square roots: \[ \sqrt{\frac{1}{20}} = \frac{\sqrt{1}}{\sqrt{20}} = \frac{1}{\sqrt{20}} = \frac{1}{\sqrt{4 \times 5}} = \frac{1}{2\sqrt{5}} \]
- Thus, the simplified expression is: \[ \frac{1}{2\sqrt{5}} \]
2. Geometry Applications
In geometry, the square root of 1/20 can be used to determine dimensions in various shapes. For example:
- Finding the side of a square with an area of \( \frac{1}{20} \) square units:
- The area \( A \) of a square is given by \( A = s^2 \), where \( s \) is the side length.
- Given \( A = \frac{1}{20} \), we solve for \( s \): \[ s = \sqrt{\frac{1}{20}} = \frac{1}{\sqrt{20}} = \frac{1}{2\sqrt{5}} \approx 0.111 \text{ units} \]
3. Engineering and Physics
In engineering and physics, precise calculations often require the use of square roots. An example involving the square root of 1/20 could be in determining tolerances or material properties:
- For a material with a tolerance factor of \( \sqrt{\frac{1}{20}} \):
- If the original measurement is 10 units, the tolerance could be calculated as: \[ \text{Tolerance} = 10 \times \sqrt{\frac{1}{20}} = 10 \times \frac{1}{2\sqrt{5}} \approx 0.5 \text{ units} \]
4. Statistical Analysis
In statistics, the square root of fractions is often used to calculate standard deviations and variances. For example:
- Calculating a variance involving the square root of 1/20:
- If the variance of a data set is \( \frac{1}{20} \), the standard deviation (σ) is: \[ \sigma = \sqrt{\frac{1}{20}} = \frac{1}{2\sqrt{5}} \approx 0.111 \]
These examples illustrate the versatility and importance of the square root of 1/20 in various fields. By understanding and applying this concept, one can solve a wide range of practical problems.
Further Resources and Reading
To deepen your understanding of the square root of 1/20 and related mathematical concepts, consider exploring the following resources:
-
Books:
- "The Joy of Mathematics" by Theoni Pappas - This book offers a delightful exploration of various mathematical concepts, including square roots.
- "Algebra and Trigonometry" by Michael Sullivan - A comprehensive guide that covers the basics and complexities of algebra and trigonometry, perfect for understanding square roots in detail.
-
Online Articles and Tutorials:
- - This article explains how to simplify square roots and includes practical examples.
- - Detailed explanations and examples of finding square roots for numbers from 1 to 20.
-
Educational Websites:
- - Free lessons and practice problems to help you master square roots and other algebraic concepts.
- - A resourceful site for various mathematical topics, including square roots, with practice tests and solved examples.
-
Mathematics Forums and Communities:
- - A question-and-answer site for people studying math at any level and professionals in related fields. You can ask questions and get answers from the community.
- - A subreddit for math discussions, questions, and resources shared by enthusiasts and experts alike.
These resources will provide a wide range of information and tools to enhance your understanding and application of square roots, including the square root of 1/20.
Video này giới thiệu cách tính hình vuông và căn vuông của các số từ 1 đến 20. Một tài nguyên hữu ích để nâng cao hiểu biết toán học của bạn.
Hình Vuông Các Số। Vuông Của Số। Vuông Từ 1 Đến 20। Căn Vuông Từ 1 Đến 20। Toán Học Vuông
READ MORE:
Video này trình bày cách tính căn vuông của các số từ 1 đến 20. Một tài liệu ngắn gọn và hữu ích để hiểu về căn vuông trong toán học.
Căn Vuông Từ 1 Đến 20 #shorts #toán học