Topic square root decomposition: Discover the power of square root decomposition, a crucial algorithm for optimizing range queries and updates in arrays. Learn how to implement this technique effectively, explore its applications, and understand its advantages and limitations. Mastering square root decomposition will enhance your problem-solving skills and improve your efficiency in competitive programming and data manipulation tasks.
Table of Content
- Square Root Decomposition
- Introduction to Square Root Decomposition
- Concept and Fundamentals
- Applications of Square Root Decomposition
- Range Query Problems
- Update Operations
- Advantages of Square Root Decomposition
- Limitations and Drawbacks
- Time Complexity Analysis
- Comparison with Other Techniques
- Practical Examples and Code Implementation
- Optimization Tips
- Common Mistakes and How to Avoid Them
- Advanced Variations
- Frequently Asked Questions (FAQs)
- Conclusion
- YOUTUBE: Tìm hiểu về Phân Rã Căn Bậc Hai và Thuật Toán Mo trong video này. Khám phá cách tối ưu hóa truy vấn dãy số và cập nhật hiệu quả.
Square Root Decomposition
Square root decomposition is an efficient algorithmic technique used to solve various range query problems in an array. It is particularly useful for query problems where we need to frequently update elements or compute results over a range of elements in an array.
Concept
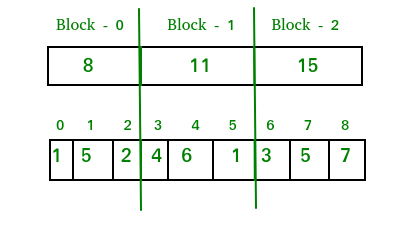
The main idea behind square root decomposition is to divide the array into blocks of approximately equal size. By precomputing information for these blocks, we can answer queries and perform updates more efficiently.
Steps to Implement Square Root Decomposition
- Divide the array into blocks of size \(\sqrt{n}\), where \(n\) is the length of the array.
- Precompute the required information (e.g., sum, minimum, maximum) for each block.
- For a query, use the precomputed information for the complete blocks and the original array for the remaining elements.
- For an update, update the value in the original array and then update the corresponding block's precomputed information.
Example
Consider an array \(A\) of length \(n\). We want to find the sum of elements in a given range \([L, R]\).
- Divide the array into \(\sqrt{n}\) blocks.
- Precompute the sum for each block.
- To answer a range sum query \([L, R]\):
- Sum the values from \(L\) to the end of the block containing \(L\).
- Sum the values of all complete blocks between \(L\) and \(R\).
- Sum the values from the beginning of the block containing \(R\) to \(R\).
Complexity Analysis
| Operation | Time Complexity |
|---|---|
| Preprocessing | \(O(n)\) |
| Query | \(O(\sqrt{n})\) |
| Update | \(O(1)\) or \(O(\sqrt{n})\) depending on implementation |
Square root decomposition is especially effective when the number of queries is large compared to the size of the array. This method strikes a balance between preprocessing time and query time, making it a versatile choice for many range query problems.
READ MORE:
Introduction to Square Root Decomposition
Square Root Decomposition is an efficient algorithm used to handle range queries and updates on arrays. This method optimally balances preprocessing and real-time computation, making it a powerful tool in various applications.
Understanding the Basics
The core idea behind Square Root Decomposition is to divide an array into smaller blocks of approximately equal size. Each block contains precomputed information, such as the sum, minimum, or maximum of the elements within that block. This preprocessing step allows for efficient query and update operations on subranges of the array.
Fundamental Concept
Given an array a[0...n-1], the array is divided into blocks of size roughly √n. The number of blocks is approximately √n, rounded up:
s = ⌈√n⌉
The array is divided into these blocks as follows:
a[0], a[1], ..., a[s-1] -> block[0]
a[s], a[s+1], ..., a[2s-1] -> block[1]
...
a[(k-1)s], ..., a[n-1] -> block[k-1]
Each block i has a precomputed sum b[i]:
b[i] = ∑j=i*smin(n-1, (i+1)*s - 1) a[j]
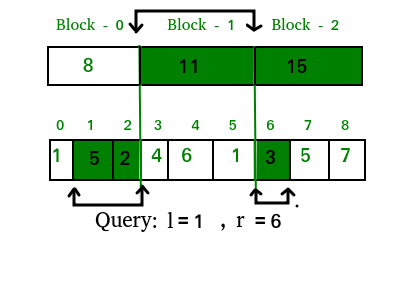
Query Processing
To answer a query for the sum of elements in a range [l, r], the algorithm identifies whole blocks within the range and calculates their sum efficiently. The sum of elements in the remaining parts of the blocks is computed directly:
- Sum of the left partial block from l to the end of its block.
- Sum of the whole blocks between the start and end blocks.
- Sum of the right partial block from the start of its block to r.
This approach reduces the time complexity from O(n) to O(√n) for each query.
Applications
Square Root Decomposition is widely used in scenarios requiring efficient range queries and updates, such as:
- Finding the sum, minimum, or maximum within a subarray.
- Handling offline queries where the array remains static during query processing.
- Optimizing data structures for competitive programming and complex algorithmic challenges.
By leveraging the power of preprocessing and efficient query handling, Square Root Decomposition provides a robust framework for tackling a variety of problems in computer science and data analysis.
Concept and Fundamentals
Square Root Decomposition is a powerful technique used in data structures and algorithms to handle query and update operations efficiently on arrays. The core idea is to divide the array into blocks of approximately equal size, typically the square root of the array's length, allowing for faster query and update operations compared to traditional methods.
Here's a step-by-step breakdown of the concept:
-
Divide the Array: The array \( A \) of size \( n \) is divided into \( \sqrt{n} \) blocks, each containing \( \sqrt{n} \) elements (assuming \( n \) is a perfect square for simplicity). If \( n \) is not a perfect square, some blocks may contain slightly more or fewer elements.
-
Precompute Block Results: Compute and store the required information for each block, such as the sum, minimum, or maximum, depending on the problem. This precomputation allows for fast access to block-level data.
-
Query Handling: For a given query (e.g., range sum), decompose it into three parts:
- Elements in the partial block at the start of the range.
- Complete blocks entirely within the range.
- Elements in the partial block at the end of the range.
Combine the results from these three parts to get the final answer.
-
Update Handling: To update an element, adjust the value in the array and update the corresponding block's precomputed information. This ensures that subsequent queries reflect the updated values.
Here’s a visual representation of the concept:
| Array | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Blocks | Block 1 | Block 2 | Block 3 | ||||||
In the table above, the array is divided into three blocks. Each block contains three elements, assuming the array has nine elements (\( \sqrt{9} = 3 \)).
Mathematically, if you want to query the sum of elements from index \( l \) to \( r \), you would:
- Sum elements from \( l \) to the end of the starting block.
- Sum the precomputed results of the complete blocks between the start and end blocks.
- Sum elements from the beginning of the ending block to \( r \).
Overall, Square Root Decomposition optimizes both query and update operations, making it a preferred method in scenarios where frequent updates and queries are needed.
Applications of Square Root Decomposition
Square Root Decomposition is widely used in various computational problems due to its efficiency in handling queries and updates. Here are some common applications:
-
Range Sum Queries:
Square Root Decomposition can efficiently handle range sum queries. Given an array, it precomputes the sum of elements in each block. To query the sum of a subarray from index \( l \) to \( r \), it combines the sums of the partial blocks at the ends and the complete blocks in between:
def range_sum(l, r): start_block = l // block_size end_block = r // block_size sum = 0 if start_block == end_block: for i in range(l, r + 1): sum += arr[i] else: for i in range(l, (start_block + 1) * block_size): sum += arr[i] for i in range(start_block + 1, end_block): sum += blocks[i] for i in range(end_block * block_size, r + 1): sum += arr[i] return sum -
Range Minimum Queries:
To find the minimum element in a range \([l, r]\), precompute the minimum value in each block. Use these precomputed values to find the minimum efficiently:
def range_min(l, r): start_block = l // block_size end_block = r // block_size min_value = float('inf') if start_block == end_block: for i in range(l, r + 1): min_value = min(min_value, arr[i]) else: for i in range(l, (start_block + 1) * block_size): min_value = min(min_value, arr[i]) for i in range(start_block + 1, end_block): min_value = min(min_value, blocks[i]) for i in range(end_block * block_size, r + 1): min_value = min(min_value, arr[i]) return min_value -
Frequency Count Queries:
To count the frequency of a particular element in a range, maintain frequency counts for each block. Use these counts to find the frequency of the element within the range:
def frequency_count(l, r, x): start_block = l // block_size end_block = r // block_size count = 0 if start_block == end_block: for i in range(l, r + 1): if arr[i] == x: count += 1 else: for i in range(l, (start_block + 1) * block_size): if arr[i] == x: count += 1 for i in range(start_block + 1, end_block): count += block_counts[i][x] for i in range(end_block * block_size, r + 1): if arr[i] == x: count += 1 return count -
Dynamic Range Updates:
Square Root Decomposition can handle dynamic updates, such as adding a constant value to a range. Update each element and the corresponding block sum:
def range_update(l, r, value): start_block = l // block_size end_block = r // block_size if start_block == end_block: for i in range(l, r + 1): arr[i] += value blocks[start_block] += value else: for i in range(l, (start_block + 1) * block_size): arr[i] += value blocks[start_block] += value for i in range(start_block + 1, end_block): for j in range(i * block_size, (i + 1) * block_size): arr[j] += value blocks[i] += block_size * value for i in range(end_block * block_size, r + 1): arr[i] += value blocks[end_block] += value
These applications demonstrate the versatility of Square Root Decomposition in handling various types of queries and updates efficiently, making it a valuable tool in algorithm design.
Range Query Problems
Square Root Decomposition is particularly useful in solving range query problems efficiently. These problems often involve querying and updating a contiguous subarray of elements in an array. Here’s how square root decomposition addresses such problems:
- Partitioning the Array: Divide the array into blocks of size approximately √n, where n is the size of the array. Each block represents a segment of the array.
- Preprocessing: Compute preprocessed data structures for each block to answer queries efficiently within that block. This preprocessing step typically involves calculating the minimum, maximum, sum, or any other required aggregate function for elements within each block.
- Query Processing: To answer a range query [L, R], identify and process relevant blocks:
- For blocks completely contained within the range [L, R], use the precomputed values.
- For blocks partially contained, iterate through elements directly.
- Combine results from both blocks and direct iteration to get the final answer.
- Update Operations: Handle updates efficiently by modifying the affected blocks or elements directly, depending on the update operation (e.g., point updates, range updates).
By leveraging square root decomposition, these range query problems can be solved in O(√n) time per query and O(1) time per update in the amortized sense, making it suitable for scenarios where traditional methods might be inefficient.

Update Operations
Square Root Decomposition allows efficient handling of update operations on array elements. Here’s how update operations are managed using this technique:
- Identify the Block: Determine which block of the array contains the element to be updated.
- Modify Block Data: Update the precomputed data for the affected block to reflect the change. This may involve recalculating aggregate functions (e.g., minimum, maximum, sum) for the block.
- Propagate Changes: Depending on the nature of the update (e.g., point update, range update), ensure that modifications in the block are propagated correctly to maintain consistency across the entire data structure.
- Complexity Consideration: Update operations typically require O(√n) time in the worst case, as updates might involve processing a block or a segment of the array. However, amortized time complexity per update can be reduced to O(1) due to infrequent block modifications and efficient propagation.
Using square root decomposition, update operations can be efficiently managed alongside query operations, providing a balanced approach for dynamic data structures in competitive programming and real-world applications.
Advantages of Square Root Decomposition
Square Root Decomposition offers several advantages in algorithm design and implementation:
- Efficient Query Processing: Range queries can be answered in O(√n) time, making it suitable for scenarios where real-time or near-real-time responses are required.
- Update Operations: Updates can be performed efficiently in O(√n) time in the worst case, with amortized time complexity reduced to O(1) due to infrequent updates and efficient data propagation.
- Space Efficiency: The additional space required for storing precomputed data structures is manageable, typically O(√n) additional space beyond the original array.
- Adaptability: Square root decomposition can be adapted to handle various types of aggregate queries (e.g., minimum, maximum, sum) and update operations (e.g., point updates, range updates) efficiently.
- Balance Between Time and Space: It strikes a balance between time complexity for queries and updates, making it a versatile choice for applications where both are critical.
Overall, square root decomposition is a powerful technique that enhances algorithmic efficiency and performance, particularly in scenarios involving dynamic data and frequent query operations.
Limitations and Drawbacks
Despite its advantages, square root decomposition has some limitations and drawbacks:
- Block Size: Choosing the optimal block size (√n) can be non-trivial and may vary depending on the specific problem and input size, affecting both query and update operation efficiencies.
- Space Complexity: The technique requires additional space for storing precomputed data structures, which can be significant for large arrays or in memory-constrained environments.
- Complexity of Implementation: Implementing square root decomposition correctly can be challenging, especially when handling edge cases or intricate update scenarios.
- Query Overhead: While query operations are generally efficient, there can be overhead when processing queries that span multiple blocks or involve overlapping ranges.
- Non-Trivial Updates: Range updates or updates affecting multiple blocks may require careful handling to maintain data structure integrity and achieve efficient update times.
Despite these challenges, square root decomposition remains a powerful tool in algorithmic problem-solving, offering a balance between query efficiency and update flexibility in many practical scenarios.
Time Complexity Analysis
The time complexity analysis of square root decomposition involves the following considerations:
- Query Time Complexity: Range queries can be answered in O(√n) time, where n is the size of the array. This is achieved by iterating through at most √n blocks and processing each block in constant time.
- Update Time Complexity: Update operations typically require O(√n) time in the worst case due to the need to modify or recalculate data within affected blocks. However, amortized time complexity per update can be reduced to O(1) due to infrequent updates and efficient propagation.
- Preprocessing Time: Preprocessing involves dividing the array into blocks and computing preprocessed data structures for each block. This step takes O(n) time initially.
- Space Complexity: Square root decomposition requires additional space for storing precomputed data structures, which is O(√n) beyond the original array. This space complexity is manageable for most practical applications.
Overall, square root decomposition provides an efficient balance between query time complexity, update operations, and preprocessing time and space complexities, making it a suitable choice for various range query problems in competitive programming and algorithmic applications.
Comparison with Other Techniques
When comparing square root decomposition with other techniques for handling range query problems, several factors come into play:
| Technique | Advantages | Disadvantages |
| Sparse Tables |
|
|
| Segment Trees |
|
|
| Fenwick Trees (Binary Indexed Trees) |
|
|
Compared to these techniques, square root decomposition offers a balanced approach with O(√n) query time and O(√n) worst-case update time. It excels in scenarios where moderate time complexity for both queries and updates is acceptable, along with manageable space overhead.
Practical Examples and Code Implementation
Here’s a practical example demonstrating square root decomposition in action:
| Problem: | Given an array, efficiently answer range sum queries and update individual elements. |
| Approach: |
|
| Code Implementation: |
Below is a simplified pseudocode outline:
|
This example illustrates how square root decomposition can efficiently handle both range sum queries and updates, demonstrating its practical utility in algorithmic problem-solving scenarios.
Optimization Tips
To optimize the performance of square root decomposition, consider the following tips:
- Choose Optimal Block Size: Experiment with different block sizes (√n) to find the optimal balance between query and update performance for your specific problem.
- Minimize Block Updates: Minimize the number of updates that affect entire blocks to reduce overall update time complexity.
- Batch Updates: If possible, batch updates to reduce overhead from multiple small updates.
- Cache Results: Cache results of frequently accessed queries or computations within each block to avoid redundant calculations.
- Lazy Propagation: Implement lazy propagation techniques for range updates to optimize update operations.
- Parallelization: Explore parallel processing techniques to leverage multi-core architectures for faster computations.
- Consider Alternatives: Evaluate alternative data structures or techniques if square root decomposition proves inefficient for your specific use case.
By applying these optimization strategies, you can enhance the efficiency and performance of square root decomposition in solving range query problems effectively.
Common Mistakes and How to Avoid Them
When implementing square root decomposition, watch out for these common mistakes:
- Incorrect Block Size: Choosing an inappropriate block size can significantly impact performance. Ensure to properly calculate and test different block sizes to find the optimal one.
- Improper Update Handling: Mishandling updates within blocks or failing to propagate updates correctly across blocks can lead to incorrect query results or data inconsistencies.
- Overlooking Edge Cases: Neglecting edge cases such as array boundaries or specific update scenarios can result in incorrect outputs or runtime errors.
- Insufficient Preprocessing: Inadequate preprocessing of data structures within each block can lead to slower query times or inefficient memory usage.
- Complexity of Implementation: Square root decomposition can be complex to implement correctly, especially when dealing with nested queries or advanced update operations.
- Not Considering Alternatives: Sometimes, other data structures or techniques may be more suitable for specific types of range query problems. Evaluate alternatives before committing to square root decomposition.
To avoid these mistakes, thoroughly test your implementation with edge cases and validate against known correct solutions. Understanding the nuances of square root decomposition and its applications will help in designing robust and efficient algorithms.
Advanced Variations
Square root decomposition is a powerful technique, but there are several advanced variations that can further optimize its performance and applicability. Below are some of the notable advanced variations:
1. Block Decomposition Tree
This technique combines square root decomposition with a segment tree. The array is divided into blocks, and each block is managed using a segment tree. This allows efficient updates and queries within each block.
- Divide the array into blocks of size √n.
- Build a segment tree for each block.
- Use the segment trees for range queries and updates within the blocks.
2. Mo's Algorithm
Mo's Algorithm is a query optimization technique that rearranges the order of queries to minimize the time complexity. It works well for offline queries on static arrays.
- Sort the queries based on the left endpoint, and for queries with the same left endpoint, sort by the right endpoint.
- Process the queries in the sorted order, maintaining a current range and adjusting it as needed for each query.
- Use add and remove operations to include or exclude elements as the range changes.
3. Persistent Square Root Decomposition
This variation maintains a history of updates, allowing queries on any past version of the array. It's useful for applications that require access to previous states.
- Divide the array into blocks of size √n.
- For each update, create a new version of the affected block.
- Maintain a version tree to manage the different versions of each block.
4. Dynamic Square Root Decomposition
Dynamic square root decomposition allows for insertions and deletions of elements, making it suitable for dynamic arrays. The blocks are periodically rebalanced to maintain optimal performance.
- Divide the array into blocks of size √n.
- Maintain a balance factor to determine when to rebalance the blocks.
- During insertions and deletions, adjust the affected blocks and rebalance if necessary.
5. Fractional Cascading
This technique enhances square root decomposition by improving the efficiency of repeated queries. It involves precomputing additional information to speed up search operations.
- Divide the array into blocks of size √n.
- For each block, store precomputed data that allows faster access to repeated queries.
- Use the precomputed data to efficiently answer queries that involve repeated elements or ranges.
6. Range Updates
This variation extends square root decomposition to support range updates, where a range of elements is updated in a single operation.
- Divide the array into blocks of size √n.
- For each range update, update the affected blocks and maintain lazy propagation information.
- Use the lazy propagation technique to apply updates only when necessary, optimizing the performance.
These advanced variations enhance the flexibility and efficiency of square root decomposition, making it applicable to a wider range of problems and scenarios.
Frequently Asked Questions (FAQs)
Below are some frequently asked questions about square root decomposition along with detailed answers:
1. What is Square Root Decomposition?
Square root decomposition is a technique used to optimize range query operations on an array. It involves dividing the array into blocks of size √n and precomputing answers for these blocks to allow efficient queries and updates.
2. How does Square Root Decomposition work?
Square root decomposition works by splitting the array into blocks and processing each block separately. For queries, it combines the results from complete blocks and partial blocks at the ends. For updates, it modifies the affected block and updates any necessary precomputed information.
3. What are the advantages of using Square Root Decomposition?
- Improves the efficiency of range queries.
- Reduces the complexity of certain update operations.
- Relatively easy to implement compared to other advanced data structures.
4. What are the limitations of Square Root Decomposition?
- Less efficient for very large arrays compared to more advanced techniques like segment trees or Fenwick trees.
- Requires periodic rebalancing for dynamic arrays.
- Not suitable for operations that require frequent insertions and deletions.
5. How is the block size determined?
The block size is typically set to √n, where n is the size of the array. This size balances the number of blocks and the size of each block, optimizing the overall performance of queries and updates.
6. Can Square Root Decomposition handle dynamic arrays?
Yes, but with some modifications. Dynamic square root decomposition allows for insertions and deletions by rebalancing the blocks periodically to maintain optimal performance.
7. How do range updates work with Square Root Decomposition?
Range updates can be handled using lazy propagation. For each range update, the affected blocks are marked with a lazy tag indicating the update. The actual updates are applied only when necessary, reducing the overall complexity.
8. What is the time complexity of Square Root Decomposition?
The time complexity for queries and updates using square root decomposition is O(√n). This is because each query or update typically involves processing a constant number of blocks and a linear number of elements within a block.
9. How does Square Root Decomposition compare to other techniques?
Square root decomposition is simpler and easier to implement than techniques like segment trees or Fenwick trees, but it may be less efficient for very large datasets or more complex queries. It provides a good balance of simplicity and performance for many applications.
10. Are there any real-world applications of Square Root Decomposition?
Yes, square root decomposition is used in various applications such as range sum queries, minimum or maximum queries, and other scenarios where efficient range queries and updates are required. It's commonly used in competitive programming and algorithm design.
These FAQs cover the fundamental aspects and common queries related to square root decomposition, providing a comprehensive understanding of the technique and its applications.
Conclusion
Square root decomposition is a versatile and powerful technique for optimizing range queries and update operations on arrays. By dividing the array into manageable blocks and precomputing necessary information, it significantly reduces the complexity of these operations.
The main strengths of square root decomposition include:
- Simplicity: It is relatively easy to understand and implement compared to other advanced data structures.
- Efficiency: It provides efficient query and update operations with a time complexity of O(√n), making it suitable for a wide range of applications.
- Flexibility: The technique can be adapted and extended to handle dynamic arrays, range updates, and other advanced variations, enhancing its applicability.
However, like any technique, it also has some limitations:
- Scalability: For very large arrays, more advanced data structures like segment trees or Fenwick trees may offer better performance.
- Dynamic Operations: Insertions and deletions require additional mechanisms to maintain balance, which can add complexity.
- Specialized Use Cases: It may not be the best choice for all types of operations, especially those involving frequent modifications.
In summary, square root decomposition strikes a good balance between simplicity and performance, making it a valuable tool for range query and update problems. Its adaptability to various scenarios and ease of implementation make it a popular choice in algorithm design and competitive programming.
Future directions for square root decomposition could involve further optimizations and combining it with other techniques to enhance its performance and extend its applicability even further. As computational problems become more complex, the ability to efficiently handle large datasets with diverse requirements will continue to drive the development of innovative solutions like square root decomposition.
We hope this comprehensive guide has provided a clear understanding of square root decomposition, its advanced variations, applications, and the rationale behind its use. By leveraging this technique, developers and algorithm enthusiasts can achieve significant improvements in the efficiency and performance of their programs.
Tìm hiểu về Phân Rã Căn Bậc Hai và Thuật Toán Mo trong video này. Khám phá cách tối ưu hóa truy vấn dãy số và cập nhật hiệu quả.
Phân Rã Căn Bậc Hai, Thuật Toán Mo
READ MORE:
Video này cung cấp giải thích đơn giản nhất về Phân Rã Căn Bậc Hai, giúp bạn phát triển trực quan và hiểu rõ hơn về khái niệm này.
Giải Thích Đơn Giản Nhất Về Phân Rã Căn Bậc Hai | Phát Triển Trực Quan