Topic square root value: The square root value is a fundamental concept in mathematics, offering insights into various applications across science and engineering. This article explores the definition, properties, and methods to calculate square roots, helping you gain a deeper understanding of this essential mathematical operation.
Table of Content
- Understanding the Square Root Value
- Introduction to Square Root
- Definition and Basic Concept of Square Root
- Properties of Square Roots
- Methods to Calculate Square Roots
- Prime Factorization Method
- Long Division Method
- Using Calculators for Square Roots
- Square Roots of Negative Numbers and Imaginary Numbers
- Square Roots in Mathematics
- Square Roots in Physics
- Square Roots in Engineering
- Square Roots in Statistics
- Common Square Root Values
- Square Root Tables
- Historical Background of Square Roots
- Famous Mathematicians and the Development of Square Roots
- Square Roots in Different Number Systems
- Advanced Topics Related to Square Roots
- YOUTUBE: Xem video để hiểu rõ hơn về Square Roots và cách tính toán chúng. Có phù hợp với nội dung về giá trị căn bậc hai không?
Understanding the Square Root Value
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol \( \sqrt{} \). For example, the square root of 9 is 3 because \( 3 \times 3 = 9 \).
Basic Properties of Square Roots
- Non-negative Results: The square root of a non-negative number is always non-negative. For instance, \( \sqrt{16} = 4 \).
- Square of the Square Root: The square of the square root of a number returns the original number, \( (\sqrt{x})^2 = x \).
- Product Rule: The square root of a product is the product of the square roots, \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
- Quotient Rule: The square root of a quotient is the quotient of the square roots, \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
Calculating Square Roots
Square roots can be calculated using various methods, including:
- Prime Factorization: Break down the number into prime factors and pair them to find the square root.
- Long Division Method: A manual arithmetic method similar to long division.
- Using a Calculator: Most scientific calculators have a square root function.
Square Roots of Negative Numbers
The square root of a negative number is not a real number. Instead, it is an imaginary number. This is because there is no real number that, when squared, results in a negative number. For example, the square root of -1 is denoted as \( i \) where \( i = \sqrt{-1} \).
Square Root Table
| Number | Square Root |
|---|---|
| 1 | \( \sqrt{1} = 1 \) |
| 4 | \( \sqrt{4} = 2 \) |
| 9 | \( \sqrt{9} = 3 \) |
| 16 | \( \sqrt{16} = 4 \) |
| 25 | \( \sqrt{25} = 5 \) |
Applications of Square Roots
Square roots are used in various fields, including:
- Mathematics: Solving quadratic equations, simplifying expressions, and in calculus.
- Physics: Calculating quantities like the RMS (root mean square) values.
- Engineering: Used in various formulas and computations.
- Statistics: Determining standard deviations and variances.
Understanding square roots is fundamental to many areas of math and science, making it an essential concept to grasp.

READ MORE:
Introduction to Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. The square root is denoted by the radical symbol '√'. For example, the square root of 16 is 4, since \( 4 \times 4 = 16 \).
Mathematically, if \( x \) is the square root of \( y \), it is represented as \( x = \sqrt{y} \), or \( x^2 = y \). The square root function is defined as a one-to-one function that takes a positive number as input and returns its square root.
Square roots have both positive and negative solutions because both positive and negative values, when squared, yield a positive result. For instance, the square roots of 9 are 3 and -3 because \( 3 \times 3 = 9 \) and \( -3 \times -3 = 9 \).
Perfect Squares and Non-Perfect Squares
Recognizing perfect squares is essential in simplifying square root calculations. Perfect squares are numbers like 1, 4, 9, 16, 25, and so on, where the square root is an integer. For example, the square root of 25 is 5 because \( 5 \times 5 = 25 \).
For non-perfect squares, the square root is not an integer and is often an irrational number. For example, the square root of 2 is approximately 1.41421, which cannot be expressed as an exact fraction.
Properties of Square Roots
- The square root of a product: \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \)
- The square root of a quotient: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
- The square of a square root: \( (\sqrt{a})^2 = a \)
- Square roots of negative numbers involve imaginary numbers: \( \sqrt{-a} = i\sqrt{a} \), where \( i \) is the imaginary unit and \( i = \sqrt{-1} \)
Calculating Square Roots
There are several methods to calculate square roots, including:
- Prime factorization
- Long division method
- Using a calculator
Applications of Square Roots
Square roots are widely used in various fields such as mathematics, physics, engineering, and statistics. They are essential for solving quadratic equations, analyzing wave functions, determining areas, and in many other applications.
Definition and Basic Concept of Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. This can be expressed mathematically as follows:
If \( y \) is the square root of \( x \), then \( y^2 = x \). For example, the square roots of 16 are 4 and -4 because \( 4^2 = 16 \) and \( (-4)^2 = 16 \).
The symbol for the square root is \( \sqrt{} \), which typically denotes the principal (non-negative) square root. For instance, \( \sqrt{9} = 3 \).
Every positive number \( x \) has two square roots: \( \sqrt{x} \) and \( -\sqrt{x} \). However, the principal square root is usually the positive one.
- The square root of a perfect square (e.g., 1, 4, 9, 16) is an integer. For example, \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \).
- For non-perfect squares (e.g., 2, 3, 5), the square root is an irrational number. For instance, \( \sqrt{2} \approx 1.414 \).
The concept of square roots extends beyond positive real numbers. When dealing with negative numbers, square roots are not real. Instead, they involve imaginary numbers. For example, \( \sqrt{-1} \) is denoted as \( i \), which is the imaginary unit.
Square roots also have important properties and applications:
- Properties:
- \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \)
- \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
- \( (\sqrt{a})^2 = a \)
- Applications: Square roots are used in various fields such as mathematics, physics, engineering, and statistics.
In summary, understanding the definition and basic concept of square roots is fundamental to comprehending more advanced mathematical topics and their practical applications.
Properties of Square Roots
The square root function has several important properties that are fundamental to its behavior in mathematics. Here are some key properties of square roots:
- Non-negative Outputs: The square root of a non-negative number is also non-negative. For any non-negative number \(a\), \(\sqrt{a} \geq 0\).
- Product Property: The square root of a product is the product of the square roots. For any non-negative numbers \(a\) and \(b\): \[ \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \]
- Quotient Property: The square root of a quotient is the quotient of the square roots. For any non-negative number \(a\) and positive number \(b\): \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
- Power of a Square Root: For any non-negative number \(a\) and any integer \(n\): \[ (\sqrt{a})^n = a^{n/2} \]
- Square Root of a Square: The square root of the square of a number returns the absolute value of the original number. For any real number \(a\): \[ \sqrt{a^2} = |a| \]
- Even and Odd Properties: The square root of an even perfect square is even, and the square root of an odd perfect square is odd.
- Irrational Square Roots: If a number is not a perfect square, its square root is irrational. For example, \(\sqrt{2}\) and \(\sqrt{3}\) are irrational numbers.
- Square Root of Zero: The square root of zero is zero. \(\sqrt{0} = 0\).
These properties are useful in various mathematical contexts, including simplifying expressions, solving equations, and understanding the behavior of functions involving square roots.
Methods to Calculate Square Roots
Calculating the square root of a number can be done using several methods, ranging from simple approximations to more precise algorithmic approaches. Here are some common methods:
1. Guess and Check Method
This method involves making an initial guess, squaring it, and adjusting the guess based on whether the result is too high or too low. Repeat until the result is sufficiently accurate.
2. Using a Square Root Table
Before calculators, square root tables were used. Find the number in the table and its corresponding square root. For numbers not listed, interpolation can estimate the square root.
3. Prime Factorization Method
This method is useful for perfect squares. Factor the number into primes, pair the prime factors, and take the product of one factor from each pair. For example:
- Square root of 81: \(81 = 3 \times 3 \times 3 \times 3\), so \(\sqrt{81} = 3 \times 3 = 9\)
- Square root of 625: \(625 = 5 \times 5 \times 5 \times 5\), so \(\sqrt{625} = 5 \times 5 = 25\)
4. Long Division Method
This method is precise and useful for both perfect and non-perfect squares. Here’s an example for finding the square root of 7921:
- Group the digits in pairs from the decimal point. For 7921, it’s (79)(21).
- Find the largest number whose square is less than or equal to the first group (79). This is 8, since \(8^2 = 64\).
- Subtract \(64\) from \(79\) to get \(15\). Bring down the next pair (21), making it \(1521\).
- Double the quotient (8) to get 16. Find a digit x such that \(16x \times x \leq 1521\). This digit is 9, so the next digit in the quotient is 9.
- Repeat the process for more digits if necessary. For 7921, \(\sqrt{7921} = 89\).
5. Using a Calculator
Most calculators have a square root function. Simply enter the number and press the square root button to get an instant result.
6. Newton's Method (Newton-Raphson Method)
This iterative numerical method provides successively better approximations to the square root. Start with a guess \(x_0\) and use the formula:
\(x_{n+1} = \frac{1}{2}\left(x_n + \frac{a}{x_n}\right)\)
Continue iterating until the difference between successive approximations is within the desired accuracy.
7. Estimation by Linear Interpolation
Useful for quick estimates, this method uses known square roots of numbers close to the target value and interpolates between them. For example, to estimate \(\sqrt{18}\), use \(\sqrt{16} = 4\) and \(\sqrt{25} = 5\) and interpolate based on how close 18 is to these values.
Each method has its advantages and is suitable for different types of problems. Using these methods, you can accurately and efficiently find square roots for a variety of applications.
Prime Factorization Method
The Prime Factorization Method is an effective way to determine the square root of a given number. This method involves breaking down the number into its prime factors and then using those factors to find the square root. Here are the detailed steps:
-
Prime Factorization: Begin by expressing the given number as a product of its prime factors.
Example: To find the square root of 400, we start with its prime factorization:
\[
400 = 2 \times 2 \times 2 \times 2 \times 5 \times 5
\] -
Pairing the Factors: Group the prime factors into pairs of identical factors.
For 400, we can pair the factors as follows:
\[
(2 \times 2) \times (2 \times 2) \times (5 \times 5)
\] -
Taking One Factor from Each Pair: For each pair, take one factor out.
For 400, we take one 2 from each pair of twos and one 5 from the pair of fives:
\[
2 \times 2 \times 5 = 20
\] -
Multiplying the Selected Factors: Multiply the factors obtained in the previous step to get the square root of the original number.
For 400, multiplying the factors gives us the square root:
\[
\sqrt{400} = 20
\]
Let's look at another example:
- Find the square root of 625.
- Prime factorize 625: \[ 625 = 5 \times 5 \times 5 \times 5 \]
- Pair the factors: \[ (5 \times 5) \times (5 \times 5) \]
- Take one factor from each pair: \[ 5 \times 5 = 25 \]
- Thus, the square root of 625 is: \[ \sqrt{625} = 25 \]
This method is particularly useful for perfect squares and provides an intuitive understanding of how square roots work by utilizing the fundamental properties of prime numbers.
Long Division Method
The long division method is a classical technique for finding the square root of a number. This method is particularly useful for manual calculations and helps understand the process of finding square roots step by step. Below is a detailed explanation of the long division method:
- Separate the number into pairs: Starting from the decimal point, separate the digits into pairs (or groups of two) by putting a bar over them. If the number has an odd number of digits, the leftmost digit will be its own separate pair. For example, to find the square root of 1522756, you separate it into pairs: 15 22 75 56.
- Find the largest square: Determine the largest square less than or equal to the leftmost pair or single digit. Write this number at the top (the square root) and its square below the leftmost pair. Subtract to find the remainder. For example, the largest square less than or equal to 15 is 3 (since 32 = 9), and the remainder is 6 (15 - 9).
- Bring down the next pair: Bring down the next pair of digits next to the remainder to form a new dividend. For example, bringing down 22 next to the remainder 6 gives 622.
- Double the quotient: Double the current quotient (ignore the decimal part) and write it down. This becomes the first part of your new divisor. For example, doubling 3 gives 6.
- Find the next digit of the quotient: Choose a digit (d) such that when the new divisor (6d) is multiplied by d, the result is less than or equal to the new dividend. For example, if d = 9, then 69 × 9 = 621 which is less than 622. So, write 9 in the quotient and subtract 621 from 622 to get a remainder of 1.
- Repeat the process: Bring down the next pair and repeat the steps until you have processed all pairs of digits. For example, bringing down 75 next to 1 gives 175. Double the quotient (39), getting 78. Find a digit d where 78d × d is less than or equal to 175. Repeat these steps until all pairs are processed.
- Continue with decimal places (if needed): If there are remaining pairs or you wish to find a more precise value, continue the process by bringing down pairs of zeros.
Below is a simplified example for better understanding:
| Step | Operation | Quotient | Remainder |
| 1 | Find largest square ≤ 15 (3² = 9) | 3 | 6 |
| 2 | Bring down next pair (22) | 3 | 622 |
| 3 | Double quotient (3×2=6), Find d where 69d×d ≤ 622 (d=9) | 39 | 1 |
| 4 | Bring down next pair (75) | 39 | 175 |
| 5 | Double quotient (39×2=78), Find d where 78d×d ≤ 175 (d=2) | 392 | 19 |
| 6 | Bring down next pair (56) | 392 | 1956 |
| 7 | Double quotient (392×2=784), Find d where 784d×d ≤ 1956 (d=2) | 3922 | 0 |
The square root of 1522756 is approximately 1234. Following this method can provide a systematic approach to finding square roots without a calculator.
Using Calculators for Square Roots
Calculators provide a quick and efficient way to calculate square roots. They are designed to handle both simple and complex calculations, making them an essential tool for students, professionals, and anyone needing to perform mathematical operations. Below are detailed steps and tips for using calculators to find square roots.
Steps to Calculate Square Roots Using a Calculator
- Turn on the Calculator: Ensure your calculator is turned on and functioning correctly. Most calculators have an "ON" button that you need to press.
- Select the Square Root Function: Locate the square root button, usually denoted by the symbol
√or√x. This button may be directly accessible or require pressing a secondary function key (often labeled "2nd" or "Shift"). - Enter the Number: Input the number for which you want to find the square root. For example, to find the square root of 25, press
2followed by5. - Press the Square Root Button: After entering the number, press the square root button. The calculator will display the square root of the entered number. For instance, the square root of 25 will display as 5.
- Read the Result: View the result on the calculator display. Ensure the result is as expected and accurate to your needs.
Example Calculations
- Finding the square root of 9: Press
9, then√. The display should show3. - Finding the square root of 16: Press
1followed by6, then√. The display should show4. - Finding the square root of 100: Press
1followed by0and another0, then√. The display should show10.
Using Scientific Calculators
Scientific calculators offer additional functionalities and can handle more complex square root calculations:
- Negative Numbers: For negative numbers, scientific calculators will return an imaginary number result. For example,
√-4will show2i. - Fractional Inputs: These calculators can also handle square roots of fractions. For instance,
√(1/4)will return0.5. - Complex Calculations: For more advanced calculations, you can use functions like
y√xto find the y-th root of x, which is useful in higher mathematics.
Calculator Tips
- Always double-check your entries to avoid mistakes.
- Use the memory functions on your calculator to store and recall values for multi-step problems.
- Refer to your calculator's manual for specific instructions and additional functions.
Conclusion
Calculators simplify the process of finding square roots, whether for basic numbers or more complex calculations. By following the steps outlined above, you can efficiently and accurately compute square roots, enhancing your mathematical proficiency and problem-solving skills.
Square Roots of Negative Numbers and Imaginary Numbers
The square root of a negative number cannot be expressed as a real number. This is because the square of any real number (positive or negative) is always non-negative. Therefore, to deal with square roots of negative numbers, we introduce the concept of imaginary numbers.
Imaginary numbers are based on the imaginary unit, denoted as i, where:
\[ i = \sqrt{-1} \]
Using this definition, we can express the square root of any negative number. For example, the square root of -9 is calculated as follows:
\[ \sqrt{-9} = \sqrt{9 \cdot -1} = \sqrt{9} \cdot \sqrt{-1} = 3i \]
In general, for any negative number -a (where a is positive), the square root can be expressed as:
\[ \sqrt{-a} = \sqrt{a} \cdot i \]
Complex Numbers
Imaginary numbers form the basis of complex numbers. A complex number is a number that has both a real part and an imaginary part. It is generally expressed in the form a + bi, where a and b are real numbers.
For example, 4 + 3i is a complex number, where 4 is the real part and 3i is the imaginary part.
Properties of Complex Numbers
- Addition: \((a + bi) + (c + di) = (a + c) + (b + d)i\)
- Subtraction: \((a + bi) - (c + di) = (a - c) + (b - d)i\)
- Multiplication: \((a + bi)(c + di) = (ac - bd) + (ad + bc)i\)
- Division: \(\frac{a + bi}{c + di} = \frac{(a + bi)(c - di)}{c^2 + d^2} = \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2}\)
Applications
Complex numbers and imaginary numbers have several important applications in various fields, including engineering, physics, and applied mathematics. They are essential in solving certain differential equations, analyzing electrical circuits, and representing oscillations and waveforms.
Understanding the concept of imaginary and complex numbers allows for the extension of mathematical analysis beyond the real numbers, providing solutions to problems that involve square roots of negative numbers.

Square Roots in Mathematics
The concept of square roots is fundamental in mathematics. A square root of a number x is a value that, when multiplied by itself, yields x. This can be expressed as:
\( y^2 = x \)
where \( y \) is the square root of \( x \). The principal square root, denoted by \( \sqrt{x} \), is the non-negative square root of \( x \). For example, the principal square root of 9 is 3, as:
\( \sqrt{9} = 3 \)
Additionally, every positive number \( x \) has two square roots: \( \sqrt{x} \) (positive) and \( -\sqrt{x} \) (negative). This can be written as:
\( \pm\sqrt{x} \)
Square Roots and Equations
Square roots play a crucial role in solving quadratic equations. For instance, to solve the equation:
\( x^2 = 25 \)
we find:
\( x = \pm\sqrt{25} \)
which gives:
\( x = \pm 5 \)
Properties of Square Roots
- Non-Negative Property: The principal square root of a non-negative number is always non-negative.
- Product Property: The square root of a product is the product of the square roots:
\( \sqrt{xy} = \sqrt{x} \cdot \sqrt{y} \)
- Quotient Property: The square root of a quotient is the quotient of the square roots:
\( \sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}} \) for \( y \neq 0 \)
Square Roots of Irrational Numbers
Square roots of numbers that are not perfect squares are irrational. For example, \( \sqrt{2} \) is an irrational number because it cannot be expressed as a simple fraction. This property was known to ancient Greek mathematicians, including Pythagoras and his followers.
Historical Significance
The concept of square roots has been studied since ancient times. Babylonian mathematicians used an approximation method for square roots around 1800-1600 BCE. The Greeks also made significant contributions to the understanding of square roots and their properties.
Overall, square roots are a foundational concept in mathematics, with applications ranging from solving equations to understanding geometric properties and beyond.
Square Roots in Physics
Square roots play a crucial role in various fields of physics, helping to simplify complex formulas and understand fundamental principles. Below are some key applications of square roots in physics:
- Root Mean Square (RMS) Values:
The root mean square (RMS) is a statistical measure used extensively in physics to quantify the magnitude of a varying quantity. It is particularly useful in analyzing alternating current (AC) circuits and waveforms.
- For an AC voltage or current, the RMS value is given by \( V_{RMS} = \frac{V_{peak}}{\sqrt{2}} \) for a sinusoidal wave. This value represents the equivalent DC value that delivers the same power to a resistor.
- In the context of gas molecules, the RMS speed \( v_{RMS} \) is used to describe the average speed of gas particles. It is calculated using the formula \( v_{RMS} = \sqrt{\frac{3kT}{m}} \), where \( k \) is Boltzmann's constant, \( T \) is the temperature, and \( m \) is the molecular mass.
- Waveforms and Signal Processing:
Square roots are used to calculate the RMS values of various waveforms, which is critical in signal processing and electrical engineering. For example:
- The RMS value of a triangular wave is \( V_{RMS} = \frac{V_{peak}}{\sqrt{3}} \).
- For a sawtooth wave, the RMS value is also calculated using a similar approach.
- Kinetic Theory of Gases:
In the kinetic theory of gases, the RMS speed of gas molecules is used to relate the temperature of the gas to the average kinetic energy of its molecules. This relationship is crucial for understanding concepts such as pressure and temperature in gases.
- Quantum Mechanics:
In quantum mechanics, the concept of the wave function's amplitude is often analyzed using RMS values to determine probabilities and expectations of particle positions and momenta.
Understanding the applications of square roots in these areas helps physicists and engineers to model and analyze physical systems more effectively, leading to advancements in technology and science.
Square Roots in Engineering
Square roots play a crucial role in various engineering disciplines, particularly in electrical and structural engineering. Here are some key applications:
- Electrical Engineering:
In electrical engineering, the Root Mean Square (RMS) value is essential for analyzing AC circuits. The RMS value represents the effective value of a varying voltage or current. It is particularly important for calculating power in AC circuits, where:
\[
P = V_{\text{RMS}} \cdot I_{\text{RMS}} \cdot \cos(\phi)
\]
where \(P\) is the power, \(V_{\text{RMS}}\) is the RMS voltage, \(I_{\text{RMS}}\) is the RMS current, and \(\phi\) is the phase angle between the current and voltage.The RMS value for a sinusoidal waveform is calculated as:
\[
V_{\text{RMS}} = \frac{V_{\text{peak}}}{\sqrt{2}}
\]Engineers use this value to design and analyze circuits, ensuring devices operate efficiently without overheating.
- Mechanical Engineering:
In mechanical engineering, square roots are used in various calculations, such as determining the natural frequencies of structures. The formula for the natural frequency \(f\) of a simple system is:
\[
f = \frac{1}{2\pi} \sqrt{\frac{k}{m}}
\]
where \(k\) is the stiffness of the system and \(m\) is the mass.This helps in designing structures that can withstand dynamic loads and avoid resonance.
- Civil Engineering:
In civil engineering, square roots are often used in the context of material strength and stress analysis. For example, the formula for calculating the buckling load \(P_{\text{cr}}\) of a column is:
\[
P_{\text{cr}} = \frac{\pi^2 EI}{(KL)^2}
\]
where \(E\) is the modulus of elasticity, \(I\) is the moment of inertia, \(K\) is the column effective length factor, and \(L\) is the actual length of the column.This formula ensures the stability and safety of structures under compressive loads.
Overall, the application of square roots in engineering helps in creating efficient, safe, and reliable systems and structures by providing accurate calculations for design and analysis.
Square Roots in Statistics
The concept of square roots is fundamental in statistics, where it is used in various calculations and transformations to simplify data analysis and enhance interpretation.
- Standard Deviation: One of the primary applications of square roots in statistics is in the calculation of the standard deviation. The standard deviation, which measures the amount of variation or dispersion in a set of data values, is calculated by taking the square root of the variance. The variance itself is the average of the squared differences from the mean.
For example, if we have a dataset of heights of dogs:
- Calculate the mean (average) height.
- Determine the difference of each height from the mean, and square these differences.
- Find the average of these squared differences to get the variance.
- Take the square root of the variance to obtain the standard deviation.
Mathematically, if the heights are \(600 \text{mm}, 470 \text{mm}, 170 \text{mm}, 430 \text{mm}, 300 \text{mm}\), the steps are:
- Mean, \( \mu = \frac{600 + 470 + 170 + 430 + 300}{5} = 394 \text{mm} \)
- Variance, \( \sigma^2 = \frac{(600-394)^2 + (470-394)^2 + (170-394)^2 + (430-394)^2 + (300-394)^2}{5} \)
- Standard Deviation, \( \sigma = \sqrt{21704} \approx 147 \text{mm} \)
- Square Root Transformation: In statistics, transforming data using the square root is a common technique to stabilize variance and make the data more normally distributed, especially in the case of skewed data or data following a Poisson distribution.
This transformation is particularly useful in regression analysis and ANOVA (Analysis of Variance) to meet the assumptions of homoscedasticity (equal variances) and normality of residuals. The square root transformation can be represented as:
\[ y' = \sqrt{y} \]
where \( y \) is the original data value and \( y' \) is the transformed value.
- Root Mean Square Error (RMSE): Another application of square roots in statistics is the calculation of the Root Mean Square Error, which is used to measure the differences between values predicted by a model and the actual values. RMSE is given by:
\[ \text{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2} \]
where \( y_i \) are the observed values, \( \hat{y}_i \) are the predicted values, and \( n \) is the number of observations.
In summary, square roots play a crucial role in statistical calculations and transformations, helping to interpret data more effectively and ensuring that statistical models meet necessary assumptions.
Common Square Root Values
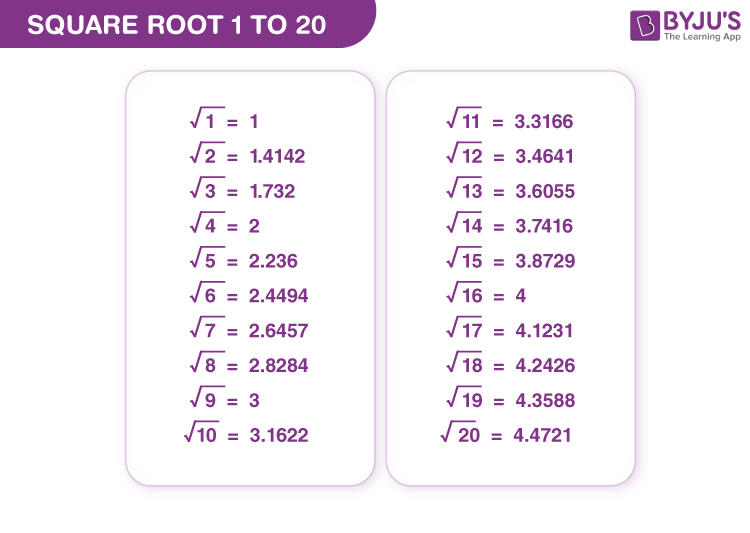
The square root of a number is a value that, when multiplied by itself, gives the original number. Here is a list of some common square root values, which are often used in various mathematical calculations:
- \(\sqrt{1} = 1\)
- \(\sqrt{2} \approx 1.414\)
- \(\sqrt{3} \approx 1.732\)
- \(\sqrt{4} = 2\)
- \(\sqrt{5} \approx 2.236\)
- \(\sqrt{6} \approx 2.449\)
- \(\sqrt{7} \approx 2.646\)
- \(\sqrt{8} \approx 2.828\)
- \(\sqrt{9} = 3\)
- \(\sqrt{10} \approx 3.162\)
These values are useful for quick reference and can help simplify calculations in various mathematical problems.
| Number | Square Root |
|---|---|
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3 |
| 10 | 3.162 |
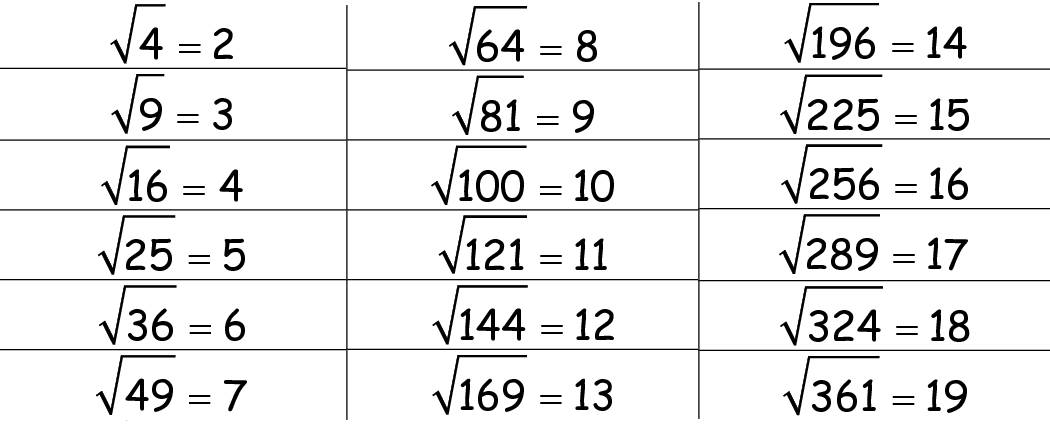
For numbers between 1 and 100, the square roots of the perfect squares are:
- \(\sqrt{1} = 1\)
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- \(\sqrt{16} = 4\)
- \(\sqrt{25} = 5\)
- \(\sqrt{36} = 6\)
- \(\sqrt{49} = 7\)
- \(\sqrt{64} = 8\)
- \(\sqrt{81} = 9\)
- \(\sqrt{100} = 10\)
These values are particularly important as they are exact integers, making them easy to work with in calculations.
Understanding these common square root values can greatly assist in solving problems in algebra, geometry, and various other fields of mathematics and science.
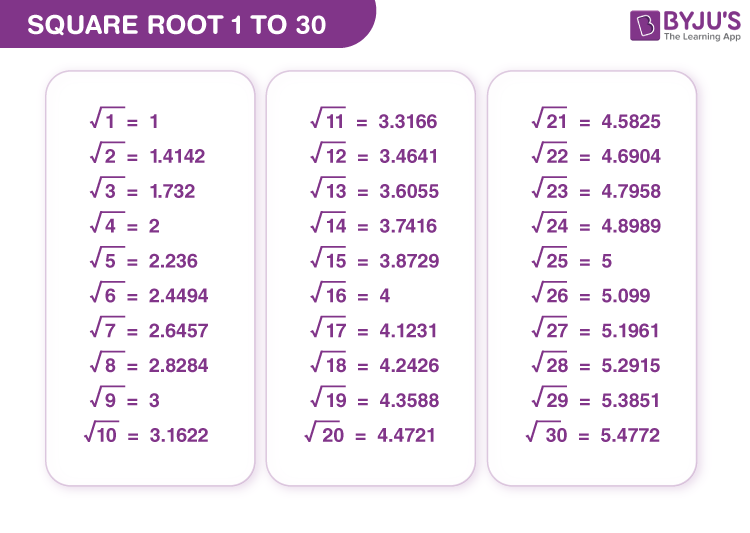
Square Root Tables
Square root tables provide a quick reference to find the square roots of perfect squares and approximate values for non-perfect squares. These tables are helpful for calculations in various fields such as mathematics, engineering, and physics. Below is a table displaying square roots for numbers 1 to 100:
| Number | Square | Square Root |
|---|---|---|
| 1 | 1 | 1.000 |
| 2 | 4 | 1.414 |
| 3 | 9 | 1.732 |
| 4 | 16 | 2.000 |
| 5 | 25 | 2.236 |
| 6 | 36 | 2.449 |
| 7 | 49 | 2.646 |
| 8 | 64 | 2.828 |
| 9 | 81 | 3.000 |
| 10 | 100 | 3.162 |
| 11 | 121 | 3.317 |
| 12 | 144 | 3.464 |
| 13 | 169 | 3.606 |
| 14 | 196 | 3.742 |
| 15 | 225 | 3.873 |
| 16 | 256 | 4.000 |
| 17 | 289 | 4.123 |
| 18 | 324 | 4.243 |
| 19 | 361 | 4.359 |
| 20 | 400 | 4.472 |
For numbers beyond this range, you can use the following method to estimate their square roots:
- Locate the closest perfect square numbers below and above the desired number.
- Use the corresponding square roots to estimate the square root of the desired number.
- For more precise calculations, use a calculator.
For example, to find the square root of 2000:
- Identify the nearest perfect squares: 1936 (44) and 2025 (45).
- The approximate square root is between 44 and 45.
- Using a calculator, you find the square root of 2000 is approximately 44.721.
Historical Background of Square Roots
The concept of square roots dates back to ancient civilizations such as Babylonian and Egyptian cultures, where numerical methods for approximating square roots were developed for practical purposes like construction and land measurement.
In ancient Greece, mathematicians like Pythagoras and Euclid studied properties of numbers, including square roots, contributing to foundational understanding. The discovery of irrational numbers, such as √2, challenged existing mathematical frameworks.
During the Islamic Golden Age, scholars such as Al-Khwarizmi advanced the understanding of algebraic techniques, including methods for solving quadratic equations involving square roots.
The Renaissance period saw renewed interest in mathematics and the formulation of algebraic symbolism, crucial for solving polynomial equations and manipulating square roots.
In the 17th and 18th centuries, European mathematicians like Descartes and Newton expanded the understanding of algebraic structures, further refining the concepts related to square roots.
Modern developments in mathematics, especially in the 19th and 20th centuries, have deepened the understanding of complex numbers and extended the application of square roots in various branches of science and technology.
Famous Mathematicians and the Development of Square Roots
1. Pythagoras (c. 570 – c. 495 BC): Founded the Pythagorean School, known for the Pythagorean Theorem and contributions to understanding square roots.
2. Euclid (c. 300 BC): Author of "Elements," which includes propositions related to geometric figures and square roots.
3. Al-Khwarizmi (c. 780 – c. 850): Persian mathematician who wrote "The Compendious Book on Calculation by Completion and Balancing," advancing algebraic techniques and methods for solving quadratic equations.
4. Rene Descartes (1596 – 1650): French mathematician and philosopher who contributed to the development of algebraic geometry and the understanding of square roots as solutions to polynomial equations.
5. Isaac Newton (1643 – 1727): English physicist and mathematician who made significant contributions to calculus and algebra, expanding the understanding of square roots in mathematical analysis.
6. Leonhard Euler (1707 – 1783): Swiss mathematician who contributed to various fields of mathematics, including number theory and algebra, further developing the theoretical basis of square roots.
7. Carl Friedrich Gauss (1777 – 1855): German mathematician who made contributions to many fields, including number theory, algebra, and statistics, refining the understanding and calculation of square roots.
Square Roots in Different Number Systems
1. Real Numbers: Square roots of non-negative real numbers are well-defined and widely used in everyday applications such as geometry and physics.
2. Complex Numbers: Every non-zero complex number has two square roots, which are typically expressed in the form \( \sqrt{a+bi} = \pm \left( \sqrt{\frac{|a+\sqrt{a^2+b^2}|}{2}} + i \cdot \mathrm{sgn}(b) \cdot \sqrt{\frac{|-a+\sqrt{a^2+b^2}|}{2}} \right) \), where \( a \) and \( b \) are real numbers.
3. Rational Numbers: Square roots of positive rational numbers that are not perfect squares are irrational, such as \( \sqrt{\frac{p}{q}} \) where \( p \) and \( q \) are coprime integers.
4. Integer Numbers: Square roots of perfect squares yield integers, while square roots of non-perfect squares are irrational numbers.
5. Binary System: In computing, square roots are often approximated using iterative methods suited for binary representations, crucial for algorithms and numerical computing.
Advanced Topics Related to Square Roots
1. Matrix Square Roots: In linear algebra, finding the square root of a matrix involves complex eigenvalue calculations and is used in various applications such as physics and engineering.
2. Continued Fractions: Representing square roots as continued fractions offers a way to approximate them with increasing accuracy, useful in number theory and algorithm design.
3. Multivalued Functions: Square roots are multivalued functions in complex analysis, requiring consideration of branch cuts and Riemann surfaces for consistent definitions and applications.
4. Functional Equations: Studying functional equations involving square roots leads to insights into symmetries and transformations in mathematical structures, impacting fields like analysis and geometry.
5. Computational Techniques: Advanced algorithms for computing square roots, such as Newton's method and the Babylonian method, optimize speed and accuracy in numerical computations and scientific simulations.
Xem video để hiểu rõ hơn về Square Roots và cách tính toán chúng. Có phù hợp với nội dung về giá trị căn bậc hai không?
Square Roots là gì? | Toán học cùng Thầy J
READ MORE:
Hướng dẫn cách tính căn bậc hai bằng tay mà không cần máy tính.
Hướng dẫn tính căn bậc hai bằng tay | Video