Topic square root 1 to 30: Welcome to our comprehensive guide on square roots from 1 to 30. Whether you're new to the concept or looking to deepen your understanding, this article covers everything from the basics of square roots to advanced topics, practical applications, and common pitfalls. Explore square root calculations, properties, real-life uses, and more, with helpful resources and practice problems included.
Table of Content
- Square Roots from 1 to 30
- Introduction to Square Roots
- Understanding the Concept of Square Roots
- Mathematical Definition of Square Roots
- Methods to Calculate Square Roots
- Properties of Square Roots
- Importance of Square Roots in Mathematics
- Square Roots from 1 to 30
- Applications of Square Roots
- Square Roots in Real Life
- Square Root Tables and Charts
- Common Mistakes When Calculating Square Roots
- Tools and Resources for Learning Square Roots
- Practice Problems and Solutions
- Advanced Topics Related to Square Roots
- Summary and Conclusion
- YOUTUBE: Xem video về các phép tính căn bậc hai và căn bậc ba từ 1 đến 30 để nâng cao hiểu biết toán học của bạn.
Square Roots from 1 to 30
In mathematics, the square root of a number is a value that, when multiplied by itself, gives the original number. Below is a detailed chart and table of the square roots from 1 to 30, including some solved examples to aid in understanding.
Square Root 1 to 30 Chart
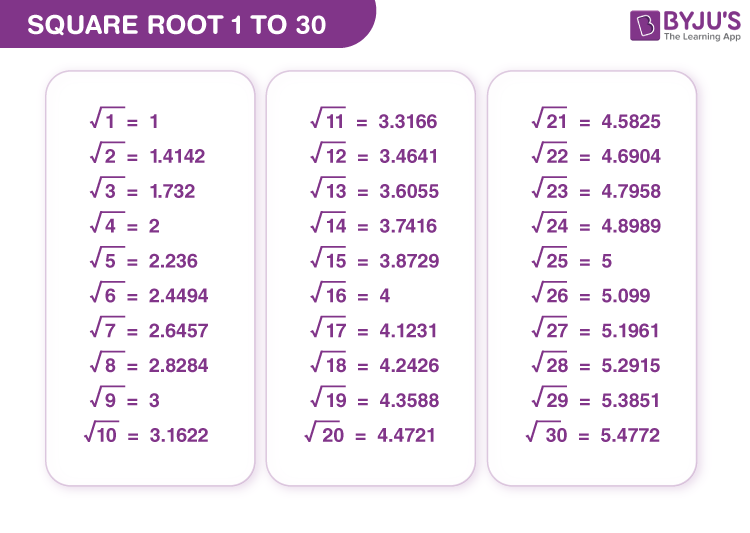
Square Root 1 to 30 Table
| \(\sqrt{1}\) | = 1 |
| \(\sqrt{2}\) | = 1.414 |
| \(\sqrt{3}\) | = 1.732 |
| \(\sqrt{4}\) | = 2 |
| \(\sqrt{5}\) | = 2.236 |
| \(\sqrt{6}\) | = 2.449 |
| \(\sqrt{7}\) | = 2.646 |
| \(\sqrt{8}\) | = 2.828 |
| \(\sqrt{9}\) | = 3 |
| \(\sqrt{10}\) | = 3.162 |
| \(\sqrt{11}\) | = 3.317 |
| \(\sqrt{12}\) | = 3.464 |
| \(\sqrt{13}\) | = 3.606 |
| \(\sqrt{14}\) | = 3.742 |
| \(\sqrt{15}\) | = 3.873 |
| \(\sqrt{16}\) | = 4 |
| \(\sqrt{17}\) | = 4.123 |
| \(\sqrt{18}\) | = 4.243 |
| \(\sqrt{19}\) | = 4.359 |
| \(\sqrt{20}\) | = 4.472 |
| \(\sqrt{21}\) | = 4.583 |
| \(\sqrt{22}\) | = 4.690 |
| \(\sqrt{23}\) | = 4.796 |
| \(\sqrt{24}\) | = 4.899 |
| \(\sqrt{25}\) | = 5 |
| \(\sqrt{26}\) | = 5.099 |
| \(\sqrt{27}\) | = 5.196 |
| \(\sqrt{28}\) | = 5.292 |
| \(\sqrt{29}\) | = 5.385 |
| \(\sqrt{30}\) | = 5.477 |
Solved Examples
Example 1
Simplify the expression: \(2\sqrt{16} + 4\)
Solution:
- Given expression: \(2\sqrt{16} + 4\)
- We know that \(\sqrt{16} = 4\)
- Substituting the value, we get \(2 \times 4 + 4 = 8 + 4 = 12\)
- Hence, the simplified form is \(12\)
Example 2
A square metal sheet has an area of \(25 \, \text{sq. inches}\). Find the length of the side of the metal sheet.
Solution:
- Let ‘a’ be the length of the side of the metal sheet
- Area = \(a^2\)
- So, \(a^2 = 25\)
- \(a = \sqrt{25} = 5 \, \text{inches}\)

READ MORE:
Introduction to Square Roots
Square roots are fundamental mathematical operations that find the side length of a square whose area matches that of a given square. When we refer to "square root 1 to 30," we're exploring the square roots of numbers from 1 to 30. Each square root, such as √1 = 1, √2 ≈ 1.414, √3 ≈ 1.732, etc., reveals the length needed to form a square with the specified area.
Understanding the Concept of Square Roots
The concept of square roots is pivotal in mathematics, particularly in understanding the relationship between numbers and geometric shapes. When we discuss "square root 1 to 30," we delve into finding a number which, when multiplied by itself, equals each number from 1 to 30. For example, √1 = 1, √2 ≈ 1.414, √3 ≈ 1.732, and so forth. This concept extends to both rational and irrational numbers, showcasing the breadth of mathematical exploration.
Mathematical Definition of Square Roots
The mathematical definition of square roots pertains to finding a number which, when multiplied by itself, yields a specified number. For numbers 1 to 30, the square root of each number is denoted as √n, where n ranges from 1 to 30. This operation uncovers the principal (positive) square root for non-negative numbers and extends into complex numbers for negative inputs, essential for various mathematical and scientific calculations.
Methods to Calculate Square Roots
Calculating square roots for numbers 1 to 30 involves several methods, each tailored to different needs:
- Estimation Method: Approximate square roots using known squares and interpolation.
- Prime Factorization: Express the number as a product of prime factors to find its square root.
- Babylonian Method: Iterative algorithm that converges to the square root through successive approximations.
- Newton's Method: Iterative method based on calculus that refines the estimate of the square root.
- Using a Calculator: Direct calculation using modern scientific calculators or software.

Properties of Square Roots
Square roots have several important properties that are fundamental to understanding their behavior and applications in mathematics. Here are some key properties:
- Non-negativity: The square root of a non-negative number is also non-negative. For any non-negative number \(x\), \(\sqrt{x} \geq 0\).
- Square Root of Zero: The square root of zero is zero. \(\sqrt{0} = 0\).
- Product Property: The square root of a product is equal to the product of the square roots of the factors. For any non-negative numbers \(a\) and \(b\), \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. For any non-negative numbers \(a\) and \(b\), where \(b \neq 0\), \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
- Power Property: The square root of a number raised to the second power returns the original number. For any non-negative number \(x\), \(\sqrt{x^2} = x\).
- Addition and Subtraction: Unlike multiplication and division, the square root of a sum or difference is not generally equal to the sum or difference of the square roots. For example, \(\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}\).
Below is a table summarizing the properties of square roots:
| Property | Description | Mathematical Expression |
|---|---|---|
| Non-negativity | The square root of a non-negative number is non-negative | \(\sqrt{x} \geq 0\) |
| Square Root of Zero | The square root of zero is zero | \(\sqrt{0} = 0\) |
| Product Property | The square root of a product is the product of the square roots | \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) |
| Quotient Property | The square root of a quotient is the quotient of the square roots | \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) |
| Power Property | The square root of a square returns the original number | \(\sqrt{x^2} = x\) |
| Addition and Subtraction | The square root of a sum or difference is not the sum or difference of the square roots | \(\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}\) |
Importance of Square Roots in Mathematics
The concept of square roots is fundamental in mathematics, providing a foundation for various mathematical operations and applications. Understanding square roots is crucial for solving equations, understanding geometric properties, and performing calculations in higher mathematics.
Here are some key points highlighting the importance of square roots in mathematics:
- Solving Quadratic Equations: Square roots are essential in solving quadratic equations. The quadratic formula, \(x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{2a}\), relies on the computation of square roots to find the solutions of the equation \(ax^2 + bx + c = 0\).
- Geometry and Trigonometry: Square roots are used to calculate distances, areas, and other geometric properties. For example, the Pythagorean theorem, \(a^2 + b^2 = c^2\), uses square roots to determine the length of the hypotenuse in a right triangle.
- Algebraic Manipulations: Square roots facilitate various algebraic manipulations and simplifications. They are used in operations involving exponents and radicals, enabling the simplification of complex expressions.
- Real and Complex Numbers: The concept of square roots extends to complex numbers, where the square root of a negative number involves imaginary units. This is crucial in advanced mathematics, including complex analysis and electrical engineering.
- Statistical Calculations: In statistics, square roots are used to calculate standard deviations, variances, and other measures of dispersion. These calculations help in understanding the distribution and variability of data.
- Physics and Engineering: Square roots are applied in various physical and engineering calculations. For example, they are used to determine the magnitude of vectors, analyze wave functions, and solve differential equations.
- Financial Mathematics: Square roots are used in financial calculations, such as determining compound interest, analyzing investment returns, and calculating risk metrics.
Square roots also play a significant role in numerical methods and algorithms used in computer science and applied mathematics. Methods like the Newton-Raphson iteration for finding roots of functions often involve square root calculations.
Overall, the importance of square roots in mathematics cannot be overstated. They are integral to understanding and solving problems across various mathematical disciplines, making them a crucial concept for students and professionals alike.
Square Roots from 1 to 30
The square root of a number is a value that, when multiplied by itself, gives the original number. Below is a detailed table listing the square roots of numbers from 1 to 30.
| Number | Square Root |
|---|---|
| 1 | 1 |
| 2 | 1.4142 |
| 3 | 1.732 |
| 4 | 2 |
| 5 | 2.236 |
| 6 | 2.4494 |
| 7 | 2.6457 |
| 8 | 2.8284 |
| 9 | 3 |
| 10 | 3.1622 |
| 11 | 3.3166 |
| 12 | 3.4641 |
| 13 | 3.6055 |
| 14 | 3.7416 |
| 15 | 3.8729 |
| 16 | 4 |
| 17 | 4.1231 |
| 18 | 4.2426 |
| 19 | 4.3588 |
| 20 | 4.4721 |
| 21 | 4.5825 |
| 22 | 4.6904 |
| 23 | 4.7958 |
| 24 | 4.8989 |
| 25 | 5 |
| 26 | 5.099 |
| 27 | 5.1961 |
| 28 | 5.2915 |
| 29 | 5.3851 |
| 30 | 5.4772 |
The square root values are critical in various mathematical applications, including geometry, algebra, and number theory. Understanding these values helps in solving equations, optimizing functions, and analyzing data. Below are a few examples to illustrate the practical use of square roots:
-
Example 1: A square metal sheet has an area of 25 square inches. To find the length of one side:
Area = \( a^2 \) = 25
\( a = \sqrt{25} = 5 \) inches
-
Example 2: A circular tabletop has an area of 16π square inches. To find the radius:
Area = \( \pi r^2 = 16\pi \)
\( r^2 = 16 \)
\( r = \sqrt{16} = 4 \) inches
Applications of Square Roots
Square roots play a vital role in various fields and applications. Understanding their usage can provide valuable insights into different scientific, engineering, and everyday contexts. Here are some key applications of square roots:
- Geometry
Square roots are essential in geometry, particularly in calculating the side length of a square given its area. For example, if the area \(A\) of a square is known, the side length is given by \(\sqrt{A}\). They are also used in the Pythagorean theorem to find the lengths of sides in right triangles.
- Physics
Square roots are used to determine various physical quantities. For instance, in kinematics, the time \(t\) it takes for an object to fall from a height \(h\) is given by \( t = \sqrt{\frac{2h}{g}} \), where \(g\) is the acceleration due to gravity.
- Statistics
In statistics, the standard deviation is a measure of data spread and is the square root of the variance. This metric helps statisticians understand data variability and distribution patterns.
- Finance
Square roots are used in finance to calculate stock volatility. The standard deviation of stock returns, which is the square root of the variance, helps investors assess the risk associated with particular stocks.
- Engineering
In electrical engineering, square roots are used to calculate root mean square (RMS) values of alternating currents and voltages, which are crucial for designing electrical circuits and systems.
- Computer Science
Square roots are used in algorithms for encryption, image processing, and computer graphics. For example, the Euclidean distance between two points in 2D or 3D space involves calculating the square root of the sum of squared differences in coordinates.
- Medicine
In medical imaging, square roots are used in algorithms that process and enhance images, such as CT scans and MRIs, to provide clearer and more accurate representations of the human body.
- Architecture
Square roots are used to determine the natural frequency of structures, which helps architects design buildings that can withstand various forces, such as wind and earthquakes.

Square Roots in Real Life
Square roots play a significant role in various real-life applications across multiple fields. Here are some of the key areas where square roots are commonly used:
- Engineering and Construction:
In engineering and construction, square roots are essential for calculations involving the Pythagorean theorem to determine distances, heights, and depths. For instance, architects use square roots to calculate the lengths of sides in right-angled triangles, ensuring structural integrity and accurate measurements.
- Physics:
Square roots are used to determine quantities such as the velocity of an object, the energy of particles, and other physical properties. For example, in wave mechanics, the square root of the energy is proportional to the amplitude of the wave.
- Finance:
In finance, square roots are used to calculate the standard deviation of returns, which is a measure of volatility. This helps investors understand the risk associated with a particular investment.
- Statistics:
Square roots are used to compute standard deviation and variance, which are critical for data analysis. These measures help statisticians understand the distribution and spread of data points in a dataset.
- Geometry:
In geometry, square roots are used to find the lengths of sides in various shapes, particularly in right triangles. The Pythagorean theorem often involves finding the square root of the sum of the squares of two sides to determine the hypotenuse.
- Computer Science and Graphics:
In computer science, square roots are used in algorithms for encryption, image processing, and game physics. For example, calculating the distance between points in a coordinate system often involves taking the square root of the sum of the squares of the differences between the coordinates.
- Navigation:
In navigation, square roots are used to calculate distances between two points on a map or globe. The distance formula in two or three dimensions involves square roots to determine the straight-line distance between points.
- Telecommunications:
In telecommunications, square roots are used to model the decay of signal strength over distance, adhering to the inverse square law, which states that the strength of a signal is inversely proportional to the square of the distance from the source.
Overall, the use of square roots is integral in solving practical problems and performing complex calculations in various disciplines, making it a fundamental mathematical concept in real-world applications.
Square Root Tables and Charts
The following table lists the square roots of numbers from 1 to 30. Square roots are a fundamental concept in mathematics, used in various calculations and problem-solving scenarios.
| Number | Square Root (√) |
|---|---|
| 1 | 1.000 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2.000 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3.000 |
| 10 | 3.162 |
| 11 | 3.317 |
| 12 | 3.464 |
| 13 | 3.606 |
| 14 | 3.742 |
| 15 | 3.873 |
| 16 | 4.000 |
| 17 | 4.123 |
| 18 | 4.243 |
| 19 | 4.359 |
| 20 | 4.472 |
| 21 | 4.583 |
| 22 | 4.690 |
| 23 | 4.796 |
| 24 | 4.899 |
| 25 | 5.000 |
| 26 | 5.099 |
| 27 | 5.196 |
| 28 | 5.292 |
| 29 | 5.385 |
| 30 | 5.477 |
Using these tables can greatly assist in various mathematical problems, including algebraic equations, geometric calculations, and statistical analyses. Having quick access to the square roots of these numbers helps enhance computational efficiency and accuracy.
Common Mistakes When Calculating Square Roots
Calculating square roots can sometimes lead to common errors, especially when the concepts are not fully understood. Here are some frequent mistakes and tips on how to avoid them:
-
Misinterpreting the Square Root Symbol: It's crucial to remember that the square root symbol (√) indicates finding a number that, when multiplied by itself, equals the original number. Confusing this with simple multiplication is a common error.
Example: \(\sqrt{0.09} = 0.3\), but sometimes mistakenly written as \(\sqrt{0.9} = 0.3\).
-
Adding Square Roots Incorrectly: Square roots cannot be added directly unless they are like terms.
Example: \(3\sqrt{3} + 3 \neq 6\sqrt{3}\). The correct expression is \(3\sqrt{3} + 3 = 3(\sqrt{3} + 1)\).
-
Distributing Square Roots Over Addition: Square roots do not distribute over addition inside the radical.
Example: \(\sqrt{x + y} \neq \sqrt{x} + \sqrt{y}\). For instance, \(\sqrt{9 + 16} \neq \sqrt{9} + \sqrt{16}\) since \(5 \neq 3 + 4\).
-
Misapplying the Pythagorean Theorem: When using the Pythagorean theorem, remember that \(\sqrt{x^2 + y^2} \neq x + y\).
Example: \(\sqrt{12^2 + 5^2} \neq 12 + 5\). The correct answer is \(\sqrt{144 + 25} = 13\).
-
Incorrectly Simplifying Square Roots: Combining non-like terms under the same radical is a mistake.
Example: \(3\sqrt{5} + 2\sqrt{5} \neq 6\sqrt{5}\). The correct expression is \(3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5}\).
-
Errors in Squaring Decimals: Ensure correct multiplication when squaring decimals.
Example: \(0.2^2 \neq 0.4\). The correct calculation is \(0.2 \times 0.2 = 0.04\).
-
Misunderstanding Exponents: When dealing with exponents, remember the proper rules of multiplication.
Example: \((4a)^2 \neq 4a^2\). The correct calculation is \((4a)^2 = 16a^2\).
-
Sign Errors in Squaring Negative Numbers: Squaring a negative number results in a positive number.
Example: \((-3)^2 \neq -9\). The correct result is \((-3) \times (-3) = 9\).
By recognizing these common mistakes, students can better understand square root calculations and avoid these pitfalls. Practice and awareness are key to mastering these concepts.
Tools and Resources for Learning Square Roots
Learning about square roots from 1 to 30 can be facilitated by a variety of tools and resources available online and in educational settings. Here’s a comprehensive list:
- Math Websites: Websites like Khan Academy, Math is Fun, and Wolfram Alpha offer tutorials, explanations, and calculators specifically designed for understanding square roots.
- Online Calculators: Utilize online calculators such as those on Symbolab or Calculator Soup to compute square roots instantly and understand the steps involved.
- Math Apps: Mobile apps like Photomath or Mathway provide interactive ways to learn and practice square root calculations on the go.
- Video Tutorials: Platforms like YouTube host numerous educational channels (e.g., Numberphile, Mathantics) with videos explaining square roots visually and intuitively.
- Books and Textbooks: Access math textbooks such as "Algebra for Dummies" or "Elementary Mathematics" by T. L. Heath, which cover square roots comprehensively.
- Interactive Games: Educational games on websites like Coolmath Games or Math Playground make learning square roots engaging and enjoyable.
- Community Forums: Participate in math forums such as Math Stack Exchange to ask questions, discuss concepts, and learn from others studying square roots.
- Practice Worksheets: Download printable worksheets from websites like Math-Aids.com or create custom exercises to reinforce understanding of square roots from 1 to 30.
Practice Problems and Solutions
Mastering square roots from 1 to 30 requires consistent practice. Below are some practice problems and solutions to help reinforce your understanding:
-
Problem 1: Calculate the square root of 9.
- Solution: \( \sqrt{9} = 3 \)
-
Problem 2: Find the square root of 16.
- Solution: \( \sqrt{16} = 4 \)
-
Problem 3: Determine the square root of 25.
- Solution: \( \sqrt{25} = 5 \)
-
Problem 4: Compute the square root of 30 (approximated to the nearest integer).
- Solution: \( \sqrt{30} \approx 5.477 \) (rounded to 5)
-
Problem 5: Solve for the square root of 1.
- Solution: \( \sqrt{1} = 1 \)
Advanced Topics Related to Square Roots
Exploring square roots beyond basic calculations unveils several advanced topics that deepen mathematical understanding:
- Complex Numbers: Understanding square roots in the context of complex numbers, where even negative numbers can have square roots.
- Algebraic Manipulations: Techniques for manipulating square roots in algebraic expressions and equations.
- Higher Order Roots: Exploring cube roots, fourth roots, and other higher order roots beyond square roots.
- Applications in Geometry: Utilizing square roots in geometric formulas such as the Pythagorean theorem and calculating distances.
- Number Theory: Connections between square roots and number theory, including perfect squares and their properties.
- Numerical Methods: Techniques for approximating square roots using iterative methods and algorithms.
- Historical Development: Tracing the historical development of square roots and their significance in ancient and modern mathematics.
- Advanced Calculus: Integration and differentiation involving square roots in calculus and their applications.
Summary and Conclusion
In conclusion, understanding square roots from 1 to 30 is fundamental in mathematics and everyday applications. Throughout this guide, we have explored:
- The concept and definition of square roots.
- Various methods to calculate square roots.
- Important properties and applications of square roots.
- Common mistakes to avoid when calculating square roots.
- Tools, resources, and practice problems available for learning and mastering square roots.
- Advanced topics related to square roots, including complex numbers, algebraic manipulations, and applications in geometry and calculus.
By mastering these concepts and utilizing the resources provided, you can enhance your mathematical skills and apply square roots effectively in real-life scenarios.
Xem video về các phép tính căn bậc hai và căn bậc ba từ 1 đến 30 để nâng cao hiểu biết toán học của bạn.
Giải pháp căn bậc hai từ 1 đến 30 | Giải pháp căn bậc ba từ 1 đến 30
READ MORE:
Xem video về các phép tính căn bậc hai và viết các số bình phương từ 1 đến 30 để nâng cao hiểu biết toán học của bạn.
Căn bậc hai từ 1 đến 30/Viết các số bình phương từ 1 đến 30/Căn bậc hai