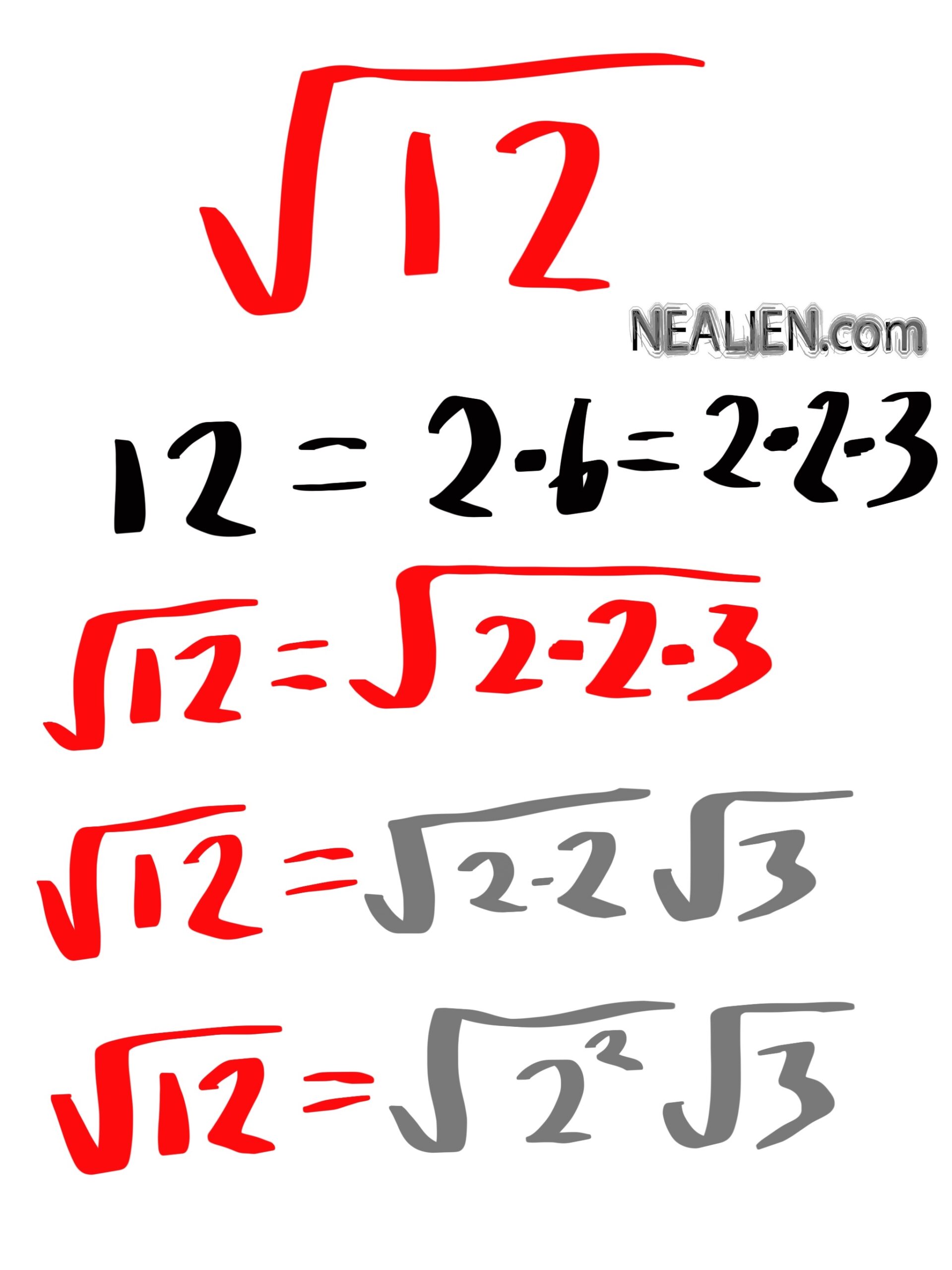Simplified Square Root of 65: A Complete Guide

To simplify the square root of 65, we need to determine if 65 can be expressed as a product of a perfect square and another number.

Steps to Simplify:

1. Factorize 65 to see if it includes a perfect square.
2. Check the prime factorization of 65: 65 = 5 × 13.
3. Neither 5 nor 13 is a perfect square.

Since 65 cannot be expressed as a product of a perfect square and another number, it is already in its simplest radical form.

Conclusion

The simplified form of \(\sqrt{65}\) remains \(\sqrt{65}\).

Simplifying square roots is a fundamental concept in mathematics that involves expressing a square root in its simplest form. This process helps in solving equations more easily and understanding the underlying properties of numbers. Here, we will take you through the steps to simplify square roots effectively.

To simplify a square root, follow these steps:

1. Find the prime factorization of the number under the square root.
2. Group the prime factors into pairs.
3. Move each pair of prime factors out of the square root.
4. If any prime factors are left unpaired, they remain under the square root.

Let's apply these steps to simplify the square root of 65:

1. Prime factorize 65: \(65 = 5 \times 13\).
2. Since 5 and 13 are both prime and do not form pairs, they remain under the square root.
3. Therefore, the square root of 65 cannot be simplified further and remains \(\sqrt{65}\).

This basic approach can be applied to any number to determine if its square root can be simplified. Understanding and mastering this method is crucial for tackling more complex mathematical problems with confidence.

A square root of a number is a value that, when multiplied by itself, gives the original number. The square root is denoted by the radical symbol \(\sqrt{}\). For example, the square root of 25 is 5 because \(5 \times 5 = 25\).

Key points to understand square roots:

• Definition: If \(x^2 = y\), then \(x\) is the square root of \(y\), written as \(x = \sqrt{y}\).
• Positive and Negative Roots: Every positive number has two square roots, one positive and one negative. For instance, the square roots of 9 are 3 and -3.
• Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are whole numbers.
• Non-Perfect Squares: Numbers that do not have whole number square roots, such as 2, 3, 5, and 65, are called non-perfect squares. Their square roots are irrational numbers.

Steps to find the square root of a non-perfect square:

1. Estimate: Find the two closest perfect squares between which the number lies. For 65, it is between 64 (\(8^2\)) and 81 (\(9^2\)).
2. Refine: Use methods like the average method or a calculator to get a more precise value.
3. Simplify (if possible): Simplify the square root by factoring out perfect squares. However, some square roots, like \(\sqrt{65}\), cannot be simplified further as they do not contain any perfect square factors other than 1.

Understanding the concept of square roots is fundamental in mathematics. It helps in solving equations, understanding geometric properties, and performing various calculations in advanced mathematical problems.

Simplifying square roots involves expressing a square root in its simplest form. This process is essential in mathematics for making calculations more manageable and understanding the properties of numbers. Here are the detailed methods to simplify square roots:

Prime Factorization Method:

1. Find the Prime Factors: Factorize the number under the square root into its prime factors. For example, for 72, we have \(72 = 2 \times 2 \times 2 \times 3 \times 3\).
2. Group the Prime Factors: Group the prime factors into pairs. Each pair of identical factors can be taken out of the square root. In the case of 72, we get \((2 \times 2) \times (3 \times 3) \times 2\).
3. Simplify: Take one factor from each pair out of the square root and multiply them together. The simplified form of \(\sqrt{72}\) is \(2 \times 3 \times \sqrt{2} = 6\sqrt{2}\).

Example: Simplifying \(\sqrt{50}\)

1. Prime factorize 50: \(50 = 2 \times 5 \times 5\).
2. Group the prime factors: \(50 = 2 \times (5 \times 5)\).
3. Simplify: Take out one 5 from the pair, giving \(5\sqrt{2}\). Hence, \(\sqrt{50} = 5\sqrt{2}\).

Perfect Square Method:

1. Identify Perfect Squares: Find the largest perfect square factor of the number under the square root.
2. Rewrite the Expression: Express the number as a product of the perfect square and another number. For example, for \(\sqrt{18}\), we rewrite it as \(\sqrt{9 \times 2}\).
3. Simplify: Take the square root of the perfect square and simplify. \(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\).

Example: Simplifying \(\sqrt{32}\)

1. Identify the largest perfect square factor: 16.
2. Rewrite 32 as \(16 \times 2\).
3. Simplify: \(\sqrt{32} = \sqrt{16 \times 2} = 4\sqrt{2}\).

These methods can simplify most square roots. However, some numbers, such as 65, do not have any perfect square factors other than 1, and thus their square roots cannot be simplified further. Understanding and mastering these methods are crucial for solving various mathematical problems effectively.

The prime factorization technique is a fundamental method for simplifying square roots. It involves breaking down a number into its prime factors and using these factors to simplify the square root expression. This method is systematic and helps in identifying whether a square root can be simplified. Here's a detailed step-by-step guide:

1. Find the Prime Factors:

   Start by finding the prime factors of the number under the square root. Prime factors are the prime numbers that multiply together to give the original number. For example, the prime factors of 60 are 2, 3, and 5, since \(60 = 2 \times 2 \times 3 \times 5\).

2. Group the Prime Factors:

   Next, group the prime factors into pairs. Each pair of identical prime factors can be taken out of the square root. For example, with \( \sqrt{60} \):
   

   
   
   • Prime factorization: \(60 = 2 \times 2 \times 3 \times 5\)
   
   
   • Grouping: \( (2 \times 2) \times 3 \times 5\)
   
   
   
   


3. Simplify the Expression:

   Take one factor from each pair out of the square root and multiply them together. Any remaining factors stay inside the square root. For \( \sqrt{60} \):
   

   
   
   • Take out one 2 from the pair of 2s: \(2\)
   
   
   • Remaining inside the square root: \(3 \times 5 = 15\)
   
   
   • Simplified form: \(2\sqrt{15}\)
   
   
   
   

Let's apply this technique to the square root of 65:

1. Find the Prime Factors:

   Prime factorize 65: \(65 = 5 \times 13\).

2. Group the Prime Factors:

   Since 5 and 13 are both prime and do not form pairs, they remain under the square root.

3. Simplify the Expression:

   As there are no pairs of prime factors, the square root cannot be simplified further. Therefore, the simplified form of \( \sqrt{65} \) is \( \sqrt{65} \).

The prime factorization technique is a powerful tool for simplifying square roots and understanding the structure of numbers. While some numbers, like 65, cannot be simplified further, this method is essential for identifying and simplifying those that can be.

When simplifying square roots, checking for perfect squares is a crucial step. A perfect square is a number that is the square of an integer. Recognizing these can greatly simplify the process. Here's how to check for perfect squares in a step-by-step manner:

1. Identify the Number:

   Start with the number under the square root. For example, let's consider the number 65.

2. List Perfect Squares:

   List some perfect squares for reference: \(1, 4, 9, 16, 25, 36, 49, 64, 81, 100,\) etc. These are squares of integers: \(1^2, 2^2, 3^2, 4^2, 5^2, 6^2, 7^2, 8^2, 9^2, 10^2,\) etc.

3. Check for Divisibility:

   Check if the given number (65) is divisible by any of these perfect squares other than 1. Divisibility by a perfect square indicates that part of the number can be simplified.
   

   
   
   • 65 is not divisible by 4, 9, 16, 25, 36, or 49.
   
   
   • 65 is only divisible by 1 (since any number is divisible by 1).
   
   
   
   


4. Determine Simplification:

   If the number is divisible by a perfect square, rewrite the number as a product of the perfect square and another number. Simplify the square root accordingly. Since 65 is not divisible by any perfect squares other than 1, it cannot be simplified further.
   

   
   
   • For example, \( \sqrt{50} \): 50 is divisible by 25 (which is \(5^2\)), so \( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \).
   
   
   
   

Applying this to \( \sqrt{65} \):

1. Identify the number: 65.
2. List perfect squares: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, etc.
3. Check for divisibility:
   • 65 ÷ 1 = 65
   • 65 ÷ 4 = not an integer
   • 65 ÷ 9 = not an integer
   • 65 ÷ 16 = not an integer
   • 65 ÷ 25 = not an integer
   • 65 ÷ 36 = not an integer
   • 65 ÷ 49 = not an integer
   • 65 ÷ 64 = not an integer
4. Determine simplification: Since 65 is not divisible by any perfect squares other than 1, \( \sqrt{65} \) cannot be simplified further.

Understanding and checking for perfect squares is a key step in the simplification process. Although some numbers like 65 cannot be simplified, this method is invaluable for identifying those that can be.

Simplifying the square root of a number involves breaking it down into its simplest form. Here is a detailed, step-by-step process to simplify square roots:

1. Identify the Number:

   Start with the number under the square root. For this example, we will simplify \(\sqrt{65}\).

2. Prime Factorization:

   Find the prime factors of the number. Prime factorization of 65 is:
   

   
   
   • 65 = 5 × 13
   
   
   
   


3. Check for Perfect Squares:

   Determine if there are any perfect square factors. Perfect squares are numbers like 1, 4, 9, 16, 25, etc. Since 5 and 13 are prime numbers and not perfect squares, there are no perfect square factors in 65.

4. Group Prime Factors:

   Group the prime factors into pairs. Each pair of identical factors can be taken out of the square root. However, in \(\sqrt{65}\), the prime factors 5 and 13 do not form pairs:
   

   
   
   • 65 = 5 × 13 (no pairs)
   
   
   
   


5. Simplify the Expression:

   Since there are no pairs of prime factors, the square root cannot be simplified further. Thus, \(\sqrt{65}\) remains \(\sqrt{65}\).

Let's summarize the steps with an example of a number that can be simplified:

Example: Simplifying \(\sqrt{72}\)

1. Identify the Number:

   The number is 72.

2. Prime Factorization:

   Prime factorize 72:
   

   
   
   • 72 = 2 × 2 × 2 × 3 × 3
   
   
   
   


3. Check for Perfect Squares:

   Identify the perfect square factors:
   

   
   
   • 72 = (2 × 2) × (3 × 3) × 2
   
   
   
   


4. Group Prime Factors:

   Group the factors into pairs:
   

   
   
   • (2 × 2) and (3 × 3) are pairs
   
   
   
   


5. Simplify the Expression:

   Take one factor from each pair out of the square root:
   

   
   
   • \(\sqrt{72} = \sqrt{(2 × 2) × (3 × 3) × 2} = 2 × 3 × \sqrt{2} = 6\sqrt{2}\)
   
   
   
   

By following these steps, you can simplify most square roots. However, some numbers, like 65, do not have any perfect square factors and thus cannot be simplified further.

To simplify the square root of 65, we follow a systematic approach to determine if it can be expressed in a simpler form. Here's the step-by-step process:

1. Identify the Number:

   The number to be simplified is 65, so we are looking to simplify \( \sqrt{65} \).

2. Prime Factorization:

   Break down 65 into its prime factors. The prime factorization of 65 is:
   

   
   
   • 65 = 5 × 13
   
   
   
   Both 5 and 13 are prime numbers.
   


3. Check for Perfect Squares:

   Perfect squares are numbers like 1, 4, 9, 16, 25, etc. Check if 65 has any perfect square factors. In this case:
   

   
   
   • 65 is not divisible by any perfect squares other than 1.
   
   
   
   


4. Group Prime Factors:

   Group the prime factors into pairs. For simplification, identical factors are taken out of the square root. However, in \(\sqrt{65}\), the prime factors 5 and 13 do not form pairs:
   

   
   
   • 65 = 5 × 13 (no pairs of identical factors)
   
   
   
   


5. Simplify the Expression:

   Since there are no pairs of prime factors to simplify, \(\sqrt{65}\) cannot be simplified further. Therefore, the square root remains in its original form:
   

   
   
   • \(\sqrt{65} = \sqrt{65}\)
   
   
   
   

Thus, the simplified form of \(\sqrt{65}\) is simply \(\sqrt{65}\). This shows that not all square roots can be simplified if the number does not have perfect square factors.

The square root of 65, denoted as √65, is an irrational number that cannot be simplified into a simpler radical form. This section explains why the square root of 65 cannot be simplified further by exploring its mathematical properties.

To understand why √65 cannot be simplified, let's review the steps for simplifying square roots:

1. Prime Factorization: We start by finding the prime factorization of 65. The number 65 can be broken down into its prime factors:
   • 65 = 5 × 13
   Since both 5 and 13 are prime numbers, the factorization cannot be simplified further into smaller factors.
2. Pairing Factors: In order to simplify a square root, we look for pairs of identical factors.
   • For example, √36 can be simplified because 36 = 6 × 6, and thus √36 = 6.
   • However, in the case of 65, there are no repeated factors (both 5 and 13 appear only once).
3. Checking for Perfect Squares: Another way to simplify is to see if 65 can be expressed as a product of perfect squares.
   • For example, √50 can be simplified because 50 = 25 × 2, and 25 is a perfect square. Thus, √50 = 5√2.
   • However, 65 = 5 × 13 does not contain any perfect square factors.

Since 65 has no pairs of identical prime factors and does not contain any perfect square factors, the square root of 65 cannot be simplified further. Thus, √65 remains in its simplest form as an irrational number.

In conclusion, √65 is already in its simplest form because:

• Its prime factorization contains no repeated factors.
• It does not include any perfect square factors.

Therefore, √65 is an irrational number and cannot be simplified into a simpler radical expression.

Simplified square roots are essential in various fields of mathematics, science, and engineering. Understanding how to simplify and apply square roots can help solve complex problems more efficiently. Here are some key applications:

1. Geometry and Trigonometry:

   Simplified square roots are frequently used in geometry and trigonometry to solve problems involving lengths, areas, and angles. For example:

   • Calculating Diagonals: The length of the diagonal in a square or rectangle can be found using the Pythagorean theorem. Simplifying the resulting square root helps in obtaining the exact length. For a square with side length a, the diagonal length is √2a.
   • Distance Formula: The distance between two points in the coordinate plane is determined using the distance formula, which often involves square roots. Simplifying these square roots provides precise distances. For points (x1, y1) and (x2, y2), the distance is √[(x2 - x1)^2 + (y2 - y1)^2].
2. Physics and Engineering:

   In physics and engineering, simplified square roots are crucial for calculations involving forces, velocities, and other vector quantities. Some examples include:

   • Kinematics: When calculating the resultant of multiple velocity components or forces, square roots help in determining the magnitude of the resultant vector. For example, the magnitude of a vector with components v_x and v_y is given by √[v_x^2 + v_y^2].
   • Wave Mechanics: The relationship between different wave properties, such as wavelength and frequency, often involves square roots. Simplifying these expressions aids in precise modeling of wave behaviors.
3. Statistics and Probability:

   Simplified square roots play a vital role in statistics, especially in standard deviation and variance calculations. Examples include:

   • Standard Deviation: Simplifying the square root in the standard deviation formula helps in understanding the spread of data. For a dataset with variance σ², the standard deviation is √σ² = σ.
   • Normal Distribution: The normal distribution curve often involves square roots in its probability density function. Simplifying these roots is essential for accurate probability calculations.
4. Construction and Architecture:

   In construction and architecture, square roots are used to calculate dimensions and ensure structures are built accurately:

   • Measurement Conversions: Simplifying square roots helps in converting between different units and ensuring precise measurements. For instance, converting diagonal measurements to horizontal and vertical distances often requires simplification of square roots.
   • Structural Analysis: Analyzing stress and load distribution in structures involves simplified square roots to determine stability and strength.

Overall, simplified square roots are indispensable in many real-world applications, providing clarity and precision in mathematical calculations across various domains.

When simplifying square roots, especially for numbers like 65, there are several common mistakes that students and enthusiasts often make. Understanding and avoiding these mistakes can help in achieving accurate results. Here are some of the most frequent errors:

• Not Identifying Perfect Squares Correctly: Ensure that you correctly identify and factor out any perfect squares. For example, in the case of √65, recognize that 65 is not a product of any perfect square factors (like 4, 9, 16, etc.).
• Incorrect Prime Factorization: When using the prime factorization method, make sure to break down the number completely into its prime factors. For 65, the prime factors are 5 and 13. Since neither is a perfect square, this indicates that √65 cannot be simplified further.
• Confusing Rational and Irrational Numbers: Remember that the square root of a non-perfect square is an irrational number. Trying to express √65 as a simple fraction will lead to incorrect results. √65 is approximately 8.062, and this should not be confused with rational approximations.
• Overlooking Simplification Opportunities: Always look for the greatest common factor that is a perfect square. However, in the case of √65, there are no perfect square factors, so it remains in its simplest form.
• Misapplying Simplification Rules: Ensure that the rules for simplifying square roots are applied correctly. For instance, √(a * b) = √a * √b only works if both a and b are non-negative. Applying this rule incorrectly can lead to significant errors.
• Ignoring Calculator Rounding Errors: When using a calculator to approximate square roots, be aware of rounding errors. For instance, while √65 is approximately 8.062, using rounded values in further calculations without acknowledging the rounding can lead to inaccuracies.
• Misinterpreting Simplified Forms: Understand that some square roots cannot be simplified into simpler radical forms. Accept that √65 is already in its simplest form, and attempting to force further simplification is a mistake.

Avoiding these common mistakes will help you accurately simplify square roots and understand the underlying principles better.

• What is the square root of 65?

  The square root of 65 is approximately 8.0622577482985. It is an irrational number, meaning it cannot be expressed as a simple fraction.

• Can the square root of 65 be simplified?

  No, the square root of 65 cannot be simplified further because 65 is not a perfect square, and its prime factors (5 and 13) do not form pairs.

• Is 65 a perfect square?

  No, 65 is not a perfect square. A perfect square is a number that can be expressed as the square of an integer. Since there is no integer whose square is 65, it is not a perfect square.

• Is the square root of 65 rational or irrational?

  The square root of 65 is an irrational number. This is because it cannot be written as a simple fraction and its decimal representation is non-repeating and non-terminating.

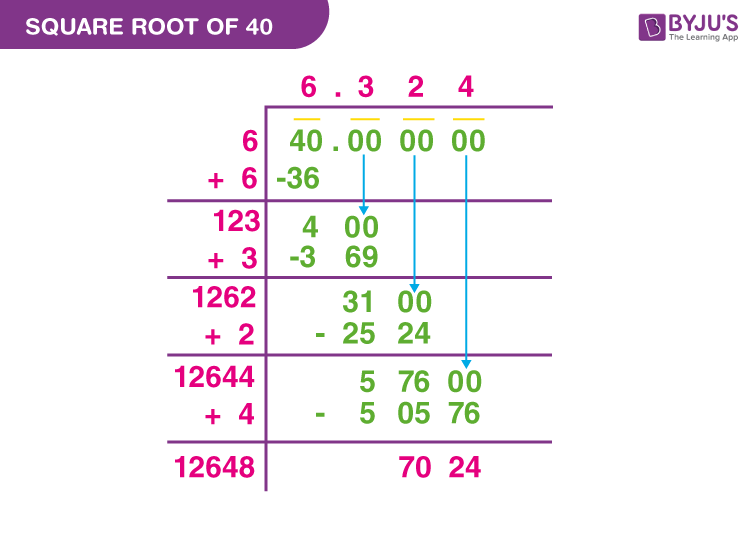
• How do you find the square root of 65 using the long division method?

  
  To find the square root of 65 using the long division method:
  

  
  
  1. Pair the digits of the number from right to left, starting with the decimal point (if any).
  
  
  2. Find the largest number whose square is less than or equal to the leftmost pair or single digit.
  
  
  3. Use this number as the divisor and the quotient.
  
  
  4. Subtract the square of the divisor from the leftmost pair or single digit and bring down the next pair of digits.
  
  
  5. Double the quotient and use it as a new divisor to find the next digit of the quotient.
  
  
  6. Repeat the process until you achieve the desired precision.
  
  
  
  


• 
  How do you express the square root of 65 in exponential form?

  The square root of 65 can be written in exponential form as \(65^{1/2}\).

• What is the decimal approximation of the square root of 65?

  The decimal approximation of the square root of 65 is 8.0622577482985.