Topic simplifying the square root: Simplifying square roots is an essential skill in mathematics that involves breaking down complex radicals into simpler forms. This article provides a comprehensive guide on various methods and examples to help you master the process of simplifying square roots. Dive in to learn more and enhance your math skills!
Table of Content
- Understanding and Simplifying Square Roots
- Introduction to Simplifying Square Roots
- Basic Concepts and Properties
- Prime Factorization Method
- Simplifying Square Roots of Perfect Squares
- Simplifying Square Roots of Non-Perfect Squares
- Simplifying Square Roots with Fractions
- Simplifying Square Roots with Variables
- Common Mistakes and Pitfalls
- Practice Problems and Solutions
- Advanced Techniques and Applications
- Conclusion and Further Resources
- YOUTUBE:
Understanding and Simplifying Square Roots
Simplifying square roots involves expressing the square root in its simplest form. Here are some methods and examples to help you master this concept.
Basic Rules for Simplifying Square Roots
- Factor the number under the square root into its prime factors.
- Pair the prime factors and move them outside the square root.
- If there are any unpaired factors, they remain under the square root.
Examples of Simplifying Square Roots
Let's go through some examples to understand the process better:
- Example: Simplify
√12
12 can be factored into 4 and 3.
√12 = √(4 × 3) = √4 × √3 = 2√3 - Example: Simplify
√45
45 can be factored into 9 and 5.
√45 = √(9 × 5) = √9 × √5 = 3√5 - Example: Simplify
√8
8 can be factored into 4 and 2.
√8 = √(4 × 2) = √4 × √2 = 2√2 - Example: Simplify
√50
50 can be factored into 25 and 2.
√50 = √(25 × 2) = √25 × √2 = 5√2
Product and Quotient Rules for Radicals
When dealing with products or quotients of square roots, we can use the following rules:
- Product Rule:
√a × √b = √(a × b) - Quotient Rule:
√(a/b) = √a / √b
Examples Using Product and Quotient Rules
- Example: Simplify
√6 × √15
√6 × √15 = √(6 × 15) = √90 = √(9 × 10) = 3√10 - Example: Simplify
√30 / √10
√30 / √10 = √(30 / 10) = √3
Advanced Simplification Techniques
For more complex expressions, breaking them down step-by-step is key:
- Example: Simplify
2√12 + 9√3
First, simplify each term individually:
2√12 = 2 × 2√3 = 4√3Then, combine like terms:
4√3 + 9√3 = (4 + 9)√3 = 13√3 - Example: Simplify
√20 × √5√2
√20 = √(4 × 5) = 2√5Then, multiply the terms:
2√5 × √5√2 = 2 × 5√2 = 10√2

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots involves reducing the number under the square root sign to its simplest form. This process makes calculations easier and expressions more concise. To simplify square roots, we use various techniques such as factoring into prime numbers and applying mathematical rules for square roots.
Here are the steps to simplify square roots:
- Identify the prime factors of the number inside the square root.
- Group the prime factors into pairs.
- For each pair of prime factors, take one factor out of the square root sign.
- Multiply the factors taken out of the square root sign.
- The remaining factors stay inside the square root sign.
For example, to simplify \( \sqrt{18} \):
- Prime factorize 18: \( 18 = 2 \times 3 \times 3 \)
- Group the factors: \( 18 = 2 \times (3 \times 3) \)
- Take one 3 out of the square root: \( \sqrt{18} = 3\sqrt{2} \)
Here is another example to simplify \( \sqrt{50} \):
- Prime factorize 50: \( 50 = 2 \times 5 \times 5 \)
- Group the factors: \( 50 = 2 \times (5 \times 5) \)
- Take one 5 out of the square root: \( \sqrt{50} = 5\sqrt{2} \)
Understanding how to simplify square roots is a fundamental skill in algebra that helps in solving more complex mathematical problems efficiently.
Basic Concepts and Properties
Understanding square roots and their properties is fundamental in mathematics. Simplifying square roots involves expressing the square root in its simplest form. Here are the key concepts and properties you need to know:
- Square of a Number: If \( n^2 = m \), then \( m \) is the square of \( n \).
- Square Root of a Number: If \( n^2 = m \), then \( n \) is a square root of \( m \). Both \( n \) and \(-n\) are square roots of \( m \).
- Positive Square Root: The principal square root is denoted by \( \sqrt{m} \) and represents the positive square root.
- Product Property of Square Roots: For nonnegative numbers \( a \) and \( b \), \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \).
- Quotient Property of Square Roots: For nonnegative numbers \( a \) and \( b \), \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
Let's look at some examples to understand these properties better:
| Example | Steps |
| \(\sqrt{36}\) | \(6\) (since \( 6^2 = 36 \)) |
| \(\sqrt{50}\) | \(\sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\) |
| \(\sqrt{\frac{9}{4}}\) | \(\frac{\sqrt{9}}{\sqrt{4}} = \frac{3}{2}\) |
By applying these properties, you can simplify square roots efficiently. For example, \(\sqrt{45}\) can be simplified to \(3\sqrt{5}\) because \(45 = 9 \times 5\) and \(\sqrt{9} = 3\).
Prime Factorization Method
The prime factorization method is a systematic approach to simplifying square roots by expressing the number as a product of its prime factors. Here are the detailed steps involved in this method:
- Prime Factorization: Break down the given number into its prime factors.
- Pairing Prime Factors: Group the identical prime factors into pairs.
- Extracting Factors: Take one factor from each pair and multiply them.
- Result: The product of the extracted factors is the simplified square root of the given number.
Let's go through a few examples to illustrate this method:
| Example 1: | Find the square root of 16 using the prime factorization method. |
| Step 1: | Prime factorize 16: \(16 = 2 \times 2 \times 2 \times 2\) |
| Step 2: | Pair the factors: \((2 \times 2) \times (2 \times 2)\) |
| Step 3: | Extract one factor from each pair: \(2 \times 2\) |
| Step 4: | Multiply the extracted factors: \(2 \times 2 = 4\) |
| Result: | \(\sqrt{16} = 4\) |
Here is another example:
| Example 2: | Find the square root of 81 using the prime factorization method. |
| Step 1: | Prime factorize 81: \(81 = 3 \times 3 \times 3 \times 3\) |
| Step 2: | Pair the factors: \((3 \times 3) \times (3 \times 3)\) |
| Step 3: | Extract one factor from each pair: \(3 \times 3\) |
| Step 4: | Multiply the extracted factors: \(3 \times 3 = 9\) |
| Result: | \(\sqrt{81} = 9\) |
This method ensures a clear and straightforward way to simplify square roots, making it easier to handle both perfect squares and non-perfect squares effectively.
Simplifying Square Roots of Perfect Squares
Square roots of perfect squares can be simplified easily because a perfect square is a number that is the product of an integer multiplied by itself. Here is a detailed step-by-step method to simplify square roots of perfect squares:
- Identify the perfect square. For example, \(64\) is a perfect square because \(8 \times 8 = 64\).
- Take the square root of the perfect square. Since \(64\) is \(8^2\), the square root of \(64\) is \(8\).
Let's go through some examples:
| \(\sqrt{36}\) | \(36\) is a perfect square because \(6 \times 6 = 36\). Thus, \(\sqrt{36} = 6\). |
| \(\sqrt{49}\) | \(49\) is a perfect square because \(7 \times 7 = 49\). Thus, \(\sqrt{49} = 7\). |
| \(\sqrt{81}\) | \(81\) is a perfect square because \(9 \times 9 = 81\). Thus, \(\sqrt{81} = 9\). |
This method is straightforward for perfect squares because the result is always an integer. Practice with various perfect squares to get comfortable with this process.
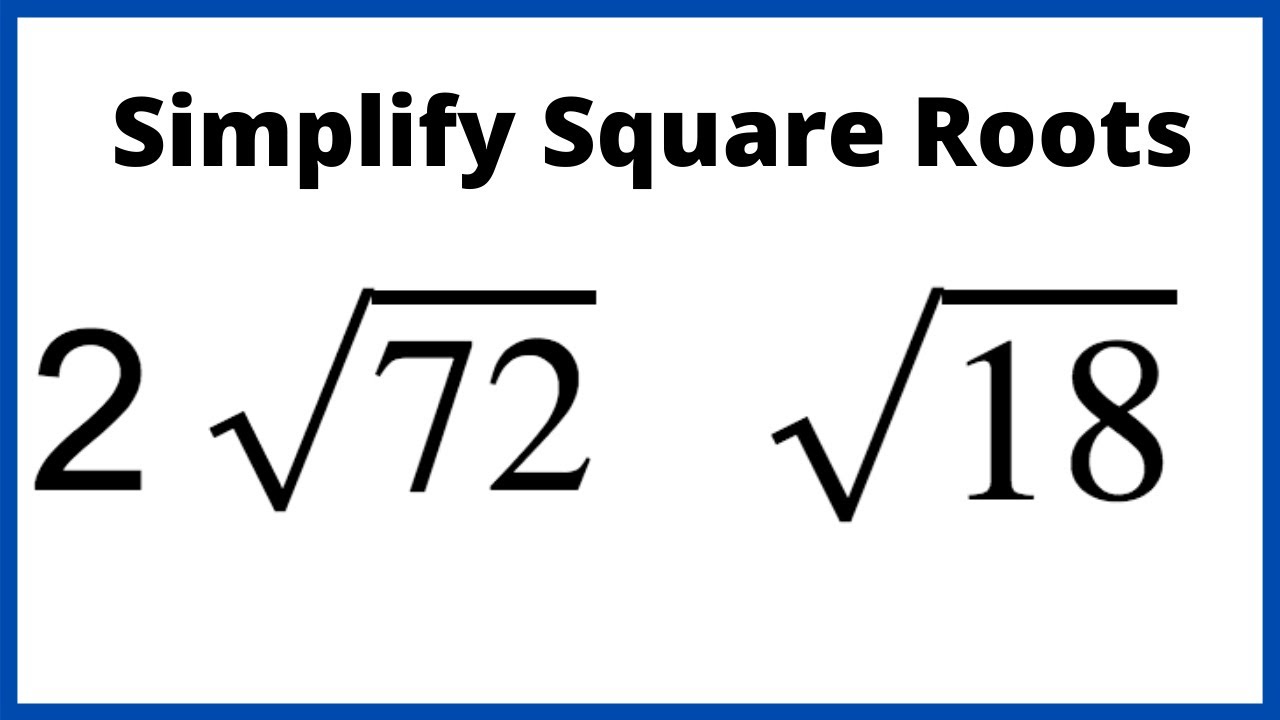
Simplifying Square Roots of Non-Perfect Squares
To simplify the square root of a non-perfect square, follow these steps:
- Identify the prime factors of the number: Break down the number inside the square root into its prime factors.
- Pair the prime factors: Group the prime factors into pairs.
- Simplify the pairs: For each pair of prime factors, move one of the factors outside the square root.
- Multiply outside the square root: Multiply the factors outside the square root together.
- Keep the remaining factors inside the square root: Any unpaired prime factors remain inside the square root.
Let's go through an example to illustrate this process:
Example:
Simplify \( \sqrt{72} \)
- Identify the prime factors:
First, find the prime factors of 72:
\( 72 = 2 \times 36 \)
\( 36 = 2 \times 18 \)
\( 18 = 2 \times 9 \)
\( 9 = 3 \times 3 \)
So, the prime factorization of 72 is:
\( 72 = 2^3 \times 3^2 \)
- Pair the prime factors:
Group the prime factors into pairs:
\( 2^3 = 2 \times 2 \times 2 \)
\( 3^2 = 3 \times 3 \)
- Simplify the pairs:
Each pair of prime factors can be simplified:
\( \sqrt{2 \times 2} = 2 \)
\( \sqrt{3 \times 3} = 3 \)
- Multiply outside the square root:
Move the pairs outside the square root and multiply them together:
\( 2 \times 3 = 6 \)
- Keep the remaining factors inside the square root:
Any unpaired prime factors remain inside the square root:
\( 2 \) remains inside the square root.
Thus, the simplified form of \( \sqrt{72} \) is:
\( \sqrt{72} = 6\sqrt{2} \)
Here are more examples to practice:
- \( \sqrt{50} = 5\sqrt{2} \)
- \( \sqrt{45} = 3\sqrt{5} \)
- \( \sqrt{98} = 7\sqrt{2} \)
Simplifying Square Roots with Fractions
Simplifying the square root of a fraction involves a few steps. We will use the Quotient Property of Square Roots, which states that for any non-negative real numbers \(a\) and \(b\) (with \(b \neq 0\)), the square root of a fraction can be expressed as the quotient of the square roots of the numerator and the denominator:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]
Let's break this down with some examples:
-
Example 1: Simplify \(\sqrt{\frac{21}{64}}\)
- Apply the Quotient Property:
- Simplify the square root of the denominator:
- Combine the results:
\[
\sqrt{\frac{21}{64}} = \frac{\sqrt{21}}{\sqrt{64}}
\]
\[
\sqrt{64} = 8
\]
\[
\sqrt{\frac{21}{64}} = \frac{\sqrt{21}}{8} -
Example 2: Simplify \(\sqrt{\frac{28}{81}}\)
- Apply the Quotient Property:
- Simplify the square roots:
\[
\sqrt{\frac{28}{81}} = \frac{\sqrt{28}}{\sqrt{81}}
\]
\[
\sqrt{81} = 9 \quad \text{and} \quad \sqrt{28} = \sqrt{4 \times 7} = 2\sqrt{7} - Combine the results:
-
Example 3: Simplify \(\sqrt{\frac{45}{100}}\)
- Apply the Quotient Property:
\[
\sqrt{\frac{45}{100}} = \frac{\sqrt{45}}{\sqrt{100}} - Simplify the square roots:
- Combine the results:
\[
\sqrt{\frac{28}{81}} = \frac{2\sqrt{7}}{9}
\[
\sqrt{100} = 10 \quad \text{and} \quad \sqrt{45} = \sqrt{9 \times 5} = 3\sqrt{5}
\[
\sqrt{\frac{45}{100}} = \frac{3\sqrt{5}}{10}
By following these steps, you can simplify the square root of any fraction. Remember to always simplify the fraction inside the radical first if possible before applying the Quotient Property. This method ensures that your final answer is in its simplest form.
Simplifying Square Roots with Variables
Simplifying square roots with variables follows a systematic approach, similar to simplifying numerical square roots. Here's a step-by-step guide:
- Identify the variables under the square root.
When you have a square root expression with variables, the first step is to identify each variable and its exponent. For example, consider the expression \(\sqrt{x^6}\).
- Rewrite the variable's exponent in terms of perfect squares.
To simplify \(\sqrt{x^6}\), express the exponent as a multiple of 2: \(x^6 = (x^3)^2\).
- Apply the square root to each term.
Use the property \(\sqrt{a^2} = a\) to simplify: \(\sqrt{(x^3)^2} = x^3\). Thus, \(\sqrt{x^6} = x^3\).
Let's look at more complex examples involving multiple variables:
- Multiple Variables Example:
Simplify \(\sqrt{x^4 y^6 z^2}\):
- Rewrite each variable's exponent: \(x^4 = (x^2)^2\), \(y^6 = (y^3)^2\), \(z^2 = (z^1)^2\).
- Apply the square root: \(\sqrt{(x^2)^2 (y^3)^2 (z^1)^2} = x^2 y^3 z\).
So, \(\sqrt{x^4 y^6 z^2} = x^2 y^3 z\).
- Variables with Odd Exponents:
When a variable has an odd exponent, separate it into a product of an even exponent and the variable itself. Simplify \(\sqrt{x^5}\):
- Rewrite: \(x^5 = x^4 \cdot x\).
- Express as a product of squares: \(x^4 = (x^2)^2\).
- Apply the square root: \(\sqrt{x^4 \cdot x} = x^2 \sqrt{x}\).
Thus, \(\sqrt{x^5} = x^2 \sqrt{x}\).
- Combination of Variables and Numbers:
Simplify \(\sqrt{18 x^3 y^4}\):
- Factorize the number: \(18 = 9 \cdot 2 = 3^2 \cdot 2\).
- Rewrite the variables: \(x^3 = x^2 \cdot x\) and \(y^4 = (y^2)^2\).
- Combine: \(\sqrt{18 x^3 y^4} = \sqrt{3^2 \cdot 2 \cdot x^2 \cdot x \cdot (y^2)^2}\).
- Apply the square root: \(3 y^2 \sqrt{2x}\).
Thus, \(\sqrt{18 x^3 y^4} = 3 y^2 \sqrt{2x}\).
By following these steps, you can simplify any square root expression involving variables systematically and accurately.
Common Mistakes and Pitfalls
When simplifying square roots, it is easy to make mistakes that can lead to incorrect answers. Understanding these common errors can help you avoid them and ensure accurate simplification. Here are some typical mistakes and pitfalls to watch out for:
-
Incorrectly Simplifying Non-Perfect Squares: A common mistake is to simplify a non-perfect square as if it were a perfect square. For example, simplifying \(\sqrt{18}\) as \(\sqrt{9 \times 2}\) without fully simplifying to \(3\sqrt{2}\).
Correct Approach: Find the largest perfect square factor.
Example:
\(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\)
-
Misapplying the Distributive Property: Incorrectly distributing square roots across addition or subtraction.
Incorrect: \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\)
Correct: \(\sqrt{a + b}\) is simplified only if the expression inside the square root can be factored into a perfect square.
Example:
Incorrect: \(\sqrt{4 + 9} = \sqrt{4} + \sqrt{9} = 2 + 3 = 5\)
Correct: \(\sqrt{4 + 9} = \sqrt{13}\)
-
Combining Unlike Radicals: Adding or subtracting radicals that are not like terms.
Incorrect: \(\sqrt{3} + \sqrt{5} = \sqrt{8}\)
Correct: Leave the expression as \(\sqrt{3} + \sqrt{5}\).
-
Forgetting to Simplify Fully: Sometimes students stop too early and do not simplify the square root completely.
Example:
Incorrect: \(\sqrt{32} = \sqrt{16 \times 2} = 4\sqrt{2}\)
Correct: Ensure no further perfect square factors remain.
\(\sqrt{32} = \sqrt{16 \times 2} = 4\sqrt{2}\) (This is correct as it is fully simplified)
-
Not Rationalizing the Denominator: Leaving a square root in the denominator is usually not preferred.
Example:
Incorrect: \(\frac{1}{\sqrt{2}}\)
Correct: Multiply numerator and denominator by \(\sqrt{2}\).
\(\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
-
Misunderstanding Even and Odd Exponents: Simplifying variables incorrectly when they have even or odd exponents.
Example:
Incorrect: \(\sqrt{x^4} = x^2\) is correct, but \(\sqrt{x^3}\) requires further simplification.
Correct: \(\sqrt{x^3} = \sqrt{x^2 \times x} = x\sqrt{x}\)
By being aware of these common mistakes, you can take care to avoid them and ensure your square root simplifications are accurate and complete.

Practice Problems and Solutions
Below are some practice problems for simplifying square roots along with their detailed solutions. Follow each step to understand the process thoroughly.
-
Simplify \( \sqrt{50} \)
Solution:
- Factor 50 into its prime factors: \( 50 = 2 \times 5^2 \)
- Rewrite the square root using these factors: \( \sqrt{50} = \sqrt{2 \times 5^2} \)
- Extract the square root of the perfect square: \( \sqrt{2 \times 5^2} = 5\sqrt{2} \)
Thus, \( \sqrt{50} = 5\sqrt{2} \)
-
Simplify \( \sqrt{72} \)
Solution:
- Factor 72 into its prime factors: \( 72 = 2^3 \times 3^2 \)
- Rewrite the square root using these factors: \( \sqrt{72} = \sqrt{2^3 \times 3^2} \)
- Extract the square root of the perfect squares: \( \sqrt{2^3 \times 3^2} = 3\sqrt{8} \)
- Further simplify \( \sqrt{8} \): \( \sqrt{8} = \sqrt{2^3} = 2\sqrt{2} \)
- Combine the results: \( 3 \times 2\sqrt{2} = 6\sqrt{2} \)
Thus, \( \sqrt{72} = 6\sqrt{2} \)
-
Simplify \( \sqrt{98} \)
Solution:
- Factor 98 into its prime factors: \( 98 = 2 \times 7^2 \)
- Rewrite the square root using these factors: \( \sqrt{98} = \sqrt{2 \times 7^2} \)
- Extract the square root of the perfect square: \( \sqrt{2 \times 7^2} = 7\sqrt{2} \)
Thus, \( \sqrt{98} = 7\sqrt{2} \)
-
Simplify \( \sqrt{200} \)
Solution:
- Factor 200 into its prime factors: \( 200 = 2^3 \times 5^2 \)
- Rewrite the square root using these factors: \( \sqrt{200} = \sqrt{2^3 \times 5^2} \)
- Extract the square root of the perfect squares: \( \sqrt{2^3 \times 5^2} = 5\sqrt{8} \)
- Further simplify \( \sqrt{8} \): \( \sqrt{8} = \sqrt{2^3} = 2\sqrt{2} \)
- Combine the results: \( 5 \times 2\sqrt{2} = 10\sqrt{2} \)
Thus, \( \sqrt{200} = 10\sqrt{2} \)
Practicing these problems will help you get comfortable with the steps involved in simplifying square roots. Make sure to factor the radicand completely and always look for pairs of prime factors.
Advanced Techniques and Applications
Understanding advanced techniques for simplifying square roots is essential for tackling complex mathematical problems in various fields. Here, we explore some of these techniques and their applications.
Nested Square Roots
Nested square roots appear in specific quadratic equations and advanced mathematical problems. Simplifying them involves recognizing patterns and using algebraic techniques.
- Identify the Pattern: Recognize the repeating pattern within the nested square roots.
- Substitution Method: Introduce a new variable to represent the nested square root, then solve the resulting equation.
Example:
Evaluate \( \sqrt{2 + \sqrt{2 + \sqrt{2 + \cdots}}} \)
- Let \( x = \sqrt{2 + \sqrt{2 + \sqrt{2 + \cdots}}} \)
- Square both sides: \( x^2 = 2 + \sqrt{2 + \sqrt{2 + \cdots}} \)
- Replace the nested square root: \( x^2 = 2 + x \)
- Solve the quadratic equation: \( x^2 - x - 2 = 0 \)
- Factorize: \( (x - 2)(x + 1) = 0 \)
- Solutions: \( x = 2 \) or \( x = -1 \)
- Since \( x \) must be positive, \( x = 2 \)
Quotient Property
The quotient property of square roots states that \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). This is useful for simplifying fractions under a square root.
- Separate the square root of the numerator and the denominator.
- Simplify each square root individually.
Example:
Simplify \( \sqrt{\frac{16}{4}} \)
- Separate the fraction: \( \sqrt{16} / \sqrt{4} \)
- Simplify: \( 4 / 2 = 2 \)
Applications in Real Life
Square roots are used in various fields including:
- Physics: Calculating the intensity of earthquakes using the Richter scale.
- Engineering: Determining material stress and strain relationships.
- Finance: Pricing European-style options using the Black-Scholes formula.
- Architecture: Designing parabolic arches and bridges.
- Healthcare: Enhancing image clarity in MRI and CT scans.
Practice Problems
- Simplify \( \sqrt{50} \)
- Factorize 50: \( 50 = 25 \times 2 \)
- Simplify: \( \sqrt{25 \times 2} = 5\sqrt{2} \)
- Simplify \( \sqrt{\frac{49}{9}} \)
- Separate the fraction: \( \sqrt{49} / \sqrt{9} \)
- Simplify: \( 7 / 3 \)
Conclusion and Further Resources
Understanding how to simplify square roots is a fundamental skill in algebra and higher-level mathematics. Throughout this guide, we have explored various techniques and methods to simplify square roots, ranging from perfect squares to more complex expressions involving variables and fractions.
Here are some key takeaways:
- Simplifying square roots involves breaking down the number under the square root into its prime factors and then pairing them appropriately.
- For non-perfect squares, you simplify by identifying and extracting the largest perfect square factor.
- When dealing with fractions under a square root, simplify the numerator and the denominator separately before simplifying the fraction as a whole.
- Square roots involving variables follow the same rules, with additional steps to handle the variable factors.
To deepen your understanding and practice more, consider exploring the following resources:
- - A comprehensive set of lessons and practice problems on simplifying square roots and other radical expressions.
- - An easy-to-follow guide with examples and explanations.
- - A detailed step-by-step guide with practice questions and answers.
By regularly practicing these techniques and referring to the resources mentioned, you will become proficient in simplifying square roots and applying this knowledge to solve more complex mathematical problems. Keep practicing and exploring, and don't hesitate to seek further help from educational platforms and math communities online.
Cách Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Đơn Giản Hóa Căn Bậc Hai | Toán Học với Thầy J






