Topic simplify the expression calculator with square roots: Discover how to simplify complex expressions involving square roots with ease using our comprehensive calculator guide. Learn key rules, methods, and examples that will help you master radical simplification. Enhance your mathematical skills and solve problems more efficiently with step-by-step instructions and practical applications.
Table of Content
- Simplify Radical Expressions Calculator with Square Roots
- Introduction
- Understanding Square Roots
- Basic Rules for Simplifying Radicals
- Methods to Simplify Square Roots
- Using Prime Factorization
- Simplifying Complex Radical Expressions
- Using Online Calculators
- Step-by-Step Examples
- Applications of Simplified Radicals
- Frequently Asked Questions
- Conclusion
- YOUTUBE:
Simplify Radical Expressions Calculator with Square Roots
Simplifying radical expressions, especially those involving square roots, can often be challenging. Using an online calculator can make this task much simpler. Below is a comprehensive guide on how to simplify square root expressions and the benefits of using a calculator for these operations.
Key Simplification Rules
- Multiplication Rule: \(\sqrt{x} \cdot \sqrt{y} = \sqrt{xy}\)
- Division Rule: \(\frac{\sqrt{x}}{\sqrt{y}} = \sqrt{\frac{x}{y}}\)
- Grouping Rule: Combine and simplify radicals under one root when possible.
Steps for Simplifying Square Roots
- Identify the radical expression and check for multiple radicals.
- If multiple radicals are present, use the multiplication or division rule to group them.
- Factor the radicand (the number under the root) to identify and extract squares.
- Simplify the expression by removing the extracted squares from under the radical.
Example Calculations
Example 1: Addition of Radicals
Simplify \(\sqrt{75} + \sqrt{12}\):
- Express each radical with its prime factors: \(\sqrt{75} = \sqrt{25 \cdot 3} = 5\sqrt{3}\), \(\sqrt{12} = \sqrt{4 \cdot 3} = 2\sqrt{3}\)
- Add the simplified terms: \(5\sqrt{3} + 2\sqrt{3} = 7\sqrt{3}\)
Example 2: Multiplication of Radicals
Simplify \(\sqrt{18} \cdot \sqrt{14}\):
- Express each radical with its prime factors: \(\sqrt{18} = \sqrt{9 \cdot 2} = 3\sqrt{2}\), \(\sqrt{14}\)
- Multiply the simplified terms: \(3\sqrt{2} \cdot \sqrt{14} = 3\sqrt{28} = 6\sqrt{7}\)
Using an Online Calculator
Online calculators simplify radical expressions by automatically applying these rules and showing step-by-step solutions. They can handle complex expressions involving addition, subtraction, multiplication, and division of radicals.
For example, the and the are powerful tools that can simplify radicals quickly and accurately.
Benefits of Using a Calculator
- Accuracy: Ensures correct application of mathematical rules.
- Efficiency: Saves time compared to manual calculations.
- Learning Aid: Provides step-by-step solutions to help understand the process.
By using these tools, you can simplify even the most complex radical expressions with confidence and ease.

READ MORE:
Introduction
Simplifying expressions with square roots is a fundamental skill in algebra that allows you to break down complex radical expressions into simpler, more manageable forms. This process involves a variety of methods and rules that help to reduce the complexity of the expressions while maintaining their original values.
Square root calculators available online, such as those from Symbolab, MathCracker, and Mathway, can aid in this simplification process. These tools not only compute the square root of a given number but also provide step-by-step solutions, ensuring a clear understanding of each simplification step.
To effectively simplify square roots, one must be familiar with a few basic rules:
- Rule 1: \(\sqrt{x} \cdot \sqrt{y} = \sqrt{xy}\)
- Rule 2: \(\sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}}\)
- Rule 3: \(\sqrt{x^2} = |x|\)
The process of simplifying square roots generally involves the following steps:
- Identify the radical expression and determine if it contains multiple radicals.
- Use Rule 1 to combine radicals that are multiplied together.
- Apply Rule 2 to handle divisions involving radicals.
- Use Rule 3 to simplify expressions where possible, removing the radical when the number under the root is a perfect square.
Online calculators simplify this process by automatically applying these rules and providing detailed explanations for each step. This not only helps in obtaining the correct result but also enhances your understanding of the underlying mathematical principles.
Understanding how to simplify square roots is essential for solving more complex mathematical problems, including those found in algebra, calculus, and beyond. It also ensures that you can express answers in their simplest form, which is crucial for further calculations and applications.
Understanding Square Roots
Square roots are a fundamental concept in mathematics, representing a value that, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3 because \(3 \times 3 = 9\). The symbol for the square root is \(\sqrt{}\).
Understanding the properties of square roots is crucial for simplifying expressions involving them. Here are some key properties:
- \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- \(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\)
- \(\sqrt{a^2} = |a|\)
To simplify a square root, we often use the prime factorization method. Here's a step-by-step process:
- Prime Factorization: Break down the number under the square root into its prime factors. For example, to simplify \(\sqrt{48}\):
- Prime factors of 48 are \(2 \times 2 \times 2 \times 2 \times 3\)
- Pair the Factors: Group the prime factors into pairs:
- \(\sqrt{2 \times 2 \times 2 \times 2 \times 3} = \sqrt{(2 \times 2) \times (2 \times 2) \times 3}\)
- Simplify: For each pair of prime factors, take one factor out of the square root:
- \(\sqrt{(2 \times 2) \times (2 \times 2) \times 3} = 2 \times 2 \times \sqrt{3} = 4\sqrt{3}\)
Not all square roots simplify neatly. For example, \(\sqrt{2}\) and \(\sqrt{3}\) cannot be simplified further because their prime factors do not form pairs.
Let's look at an example using a calculator to simplify a complex radical expression:
Consider simplifying \(\sqrt{72}\) using an online calculator:
- Enter the expression \(\sqrt{72}\) into the calculator.
- The calculator uses the prime factorization method:
- Prime factors of 72 are \(2 \times 2 \times 2 \times 3 \times 3\)
- Grouping into pairs: \(\sqrt{(2 \times 2) \times 2 \times (3 \times 3)} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\)
Using these steps, you can simplify any square root expression. Online calculators are handy tools that can perform these calculations quickly and show the step-by-step process, helping you understand the method better.
Basic Rules for Simplifying Radicals
Simplifying square roots involves expressing the number inside the root in its simplest form. Here are the basic rules and steps for simplifying radicals:
- Identify Perfect Squares: Find the largest perfect square factor of the number under the square root.
- Factor the Radicand: Express the number inside the square root as a product of two factors, one of which is the largest perfect square.
- Apply the Square Root Property: Use the property \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) to separate the factors.
- Simplify: Take the square root of the perfect square factor and simplify the expression.
Let's look at a few examples to understand these steps better:
-
Example: Simplify \(\sqrt{12}\)
- Identify the largest perfect square factor of 12, which is 4.
- Factorize: \(12 = 4 \cdot 3\)
- Apply the square root property: \(\sqrt{12} = \sqrt{4 \cdot 3} = \sqrt{4} \cdot \sqrt{3}\)
- Simplify: \(\sqrt{4} = 2\), so \(\sqrt{12} = 2\sqrt{3}\)
-
Example: Simplify \(\sqrt{45}\)
- Identify the largest perfect square factor of 45, which is 9.
- Factorize: \(45 = 9 \cdot 5\)
- Apply the square root property: \(\sqrt{45} = \sqrt{9 \cdot 5} = \sqrt{9} \cdot \sqrt{5}\)
- Simplify: \(\sqrt{9} = 3\), so \(\sqrt{45} = 3\sqrt{5}\)
-
Example: Simplify \(\sqrt{8}\)
- Identify the largest perfect square factor of 8, which is 4.
- Factorize: \(8 = 4 \cdot 2\)
- Apply the square root property: \(\sqrt{8} = \sqrt{4 \cdot 2} = \sqrt{4} \cdot \sqrt{2}\)
- Simplify: \(\sqrt{4} = 2\), so \(\sqrt{8} = 2\sqrt{2}\)
These steps can also be extended to simplify more complex expressions involving square roots:
-
Example: Simplify \(\sqrt{6} \cdot \sqrt{15}\)
- Combine the square roots: \(\sqrt{6} \cdot \sqrt{15} = \sqrt{6 \cdot 15} = \sqrt{90}\)
- Factorize: \(90 = 9 \cdot 10\)
- Apply the square root property: \(\sqrt{90} = \sqrt{9 \cdot 10} = \sqrt{9} \cdot \sqrt{10}\)
- Simplify: \(\sqrt{9} = 3\), so \(\sqrt{90} = 3\sqrt{10}\)
-
Example: Simplify \(2\sqrt{12} + 9\sqrt{3}\)
- Simplify \(2\sqrt{12}\) first: \(2\sqrt{12} = 2 \cdot 2\sqrt{3} = 4\sqrt{3}\)
- Now combine like terms: \(4\sqrt{3} + 9\sqrt{3} = (4 + 9)\sqrt{3} = 13\sqrt{3}\)
By following these rules and steps, you can simplify most radical expressions with square roots efficiently.
Methods to Simplify Square Roots
There are several methods to simplify square roots, which can make complex expressions easier to handle. Here are the most common methods:
1. Prime Factorization
Prime factorization involves breaking down the number inside the square root into its prime factors.
- Write the number as a product of prime numbers.
- Group the prime factors in pairs.
- For each pair, take one number out of the square root.
For example:
\(\sqrt{72}\)
Prime factorization: \(72 = 2 \times 2 \times 2 \times 3 \times 3\)
Grouping in pairs: \(2 \times 2\) and \(3 \times 3\)
Simplified form: \(2 \times 3 \sqrt{2} = 6 \sqrt{2}\)
2. Simplifying Fractions
Simplify the fractions inside the square root by separating the numerator and the denominator.
- Simplify the numerator and the denominator separately.
- Take the square root of the simplified numerator and denominator.
For example:
\(\sqrt{\frac{50}{2}}\)
Simplify the fraction: \(\frac{50}{2} = 25\)
Simplified form: \(\sqrt{25} = 5\)
3. Using Conjugates
When dealing with radicals in the denominator, use the conjugate to rationalize the expression.
- Multiply the numerator and the denominator by the conjugate of the denominator.
- Simplify the resulting expression.
For example:
\(\frac{1}{\sqrt{2}}\)
Multiply by conjugate: \(\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
Simplified form: \(\frac{\sqrt{2}}{2}\)
4. Combining Like Terms
Combine square root terms that have the same radicand (the number inside the square root).
- Ensure the square root terms have the same radicand.
- Combine the coefficients of these terms.
For example:
\(2\sqrt{3} + 4\sqrt{3}\)
Combine like terms: \((2 + 4)\sqrt{3} = 6\sqrt{3}\)
5. Using Online Calculators
Online calculators can be very helpful in simplifying square roots quickly and accurately. Tools like the Simplify Calculator and Mathway's Square Root Calculator can automate the process.
- Input the radical expression into the calculator.
- Select the operation you want to perform.
- View the step-by-step solution provided by the tool.
For more complex expressions, these tools can provide detailed explanations and ensure accuracy.
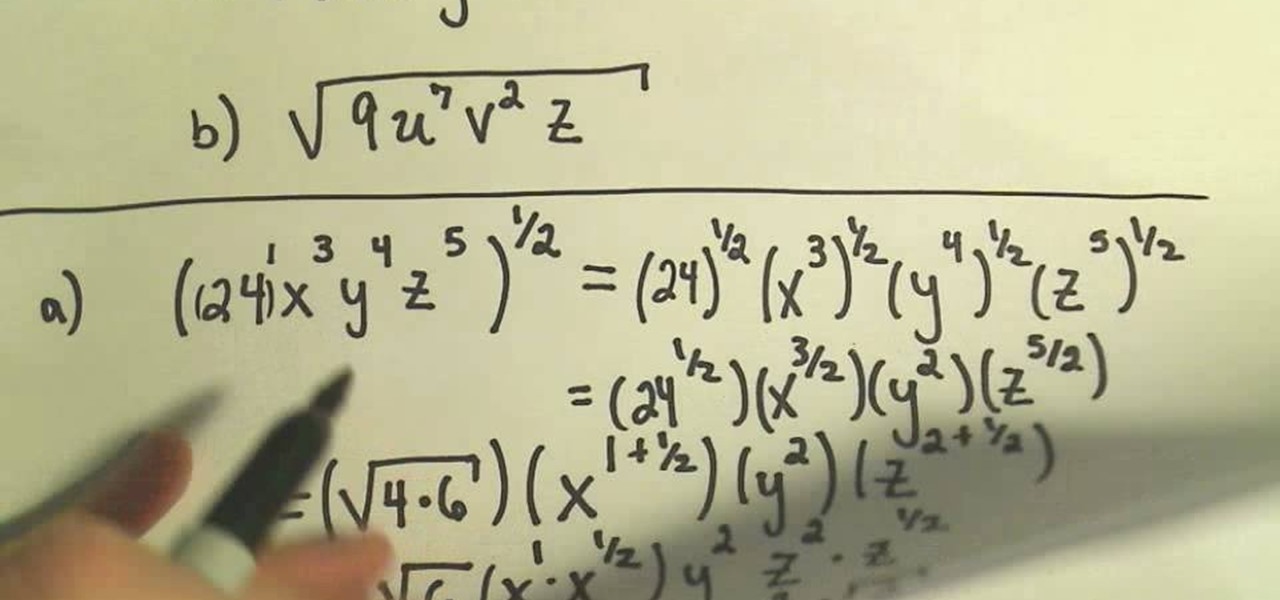
Using Prime Factorization
Prime factorization is a method used to simplify square roots by breaking down the number inside the square root into its prime factors. Here are the steps to simplify square roots using prime factorization:
- Find the prime factors: Break down the number under the square root into its prime factors.
- Group the prime factors: Pair the prime factors in groups of two.
- Move the pairs outside the square root: Each pair of prime factors can be moved outside the square root as a single number.
- Simplify the expression: Multiply the numbers outside the square root and keep the remaining factors inside the square root.
Let's look at some examples to understand this process better:
Example 1: Simplify \(\sqrt{72}\)
- Step 1: Find the prime factors of 72: \(72 = 2 \times 2 \times 2 \times 3 \times 3\)
- Step 2: Group the prime factors: \((2 \times 2) \times (2) \times (3 \times 3)\)
- Step 3: Move the pairs outside the square root: \(\sqrt{72} = 2 \times 3 \times \sqrt{2}\)
- Step 4: Simplify the expression: \(2 \times 3 = 6\), so \(\sqrt{72} = 6\sqrt{2}\)
Example 2: Simplify \(\sqrt{50}\)
- Step 1: Find the prime factors of 50: \(50 = 2 \times 5 \times 5\)
- Step 2: Group the prime factors: \((5 \times 5) \times 2\)
- Step 3: Move the pairs outside the square root: \(\sqrt{50} = 5 \times \sqrt{2}\)
- Step 4: Simplify the expression: \(\sqrt{50} = 5\sqrt{2}\)
Prime factorization is a powerful technique to simplify square roots, especially when dealing with larger numbers. By following these steps, you can make the number under the square root as small as possible, making it easier to work with in calculations and further simplifications.
Simplifying Complex Radical Expressions
Simplifying complex radical expressions involves breaking down and combining terms in a way that reduces the expression to its simplest form. Here are detailed steps to achieve this:
-
Identify and Separate Radicals: Start by identifying the radicals in the expression and separating them.
- For example, in the expression \(2\sqrt{6} + \sqrt[4]{64}\), the radicals are \(\sqrt{6}\) and \(\sqrt[4]{64}\).
-
Simplify Each Radical: Simplify each radical individually by factoring the numbers inside the radicals.
- For \(\sqrt{6}\), since 6 is 2 multiplied by 3, it remains \(\sqrt{6}\).
- For \(\sqrt[4]{64}\), since 64 is \(2^6\), it simplifies to \(2\sqrt[4]{2^2} = 2\sqrt[4]{4} = 2 \times 2 = 4\).
-
Combine Like Terms: Combine the simplified radicals, if possible. This involves adding, subtracting, multiplying, or dividing the radicals.
- In the example, after simplification, we get \(2\sqrt{6} + 4\). Since these are unlike terms, they cannot be combined further.
-
Rationalize the Denominator: If the expression involves a fraction with a radical in the denominator, multiply both the numerator and the denominator by a term that will eliminate the radical from the denominator.
- For example, to simplify \(\frac{3}{\sqrt{2}}\), multiply by \(\frac{\sqrt{2}}{\sqrt{2}}\) to get \(\frac{3\sqrt{2}}{2}\).
-
Use the Least Common Multiple (LCM): When dealing with different radicals in addition or subtraction, use the LCM to combine them under a common radical, if possible.
- For instance, to simplify \(\sqrt{2} + \sqrt[3]{4}\), find the LCM of the exponents to combine the terms effectively, although in many cases, the terms may remain separate.
By following these steps, complex radical expressions can be simplified to their most basic forms. Using these techniques ensures that the expressions are easier to work with and understand.
Using Online Calculators
Online calculators are powerful tools that can simplify radical expressions quickly and accurately. Here are the steps to use an online calculator for simplifying square roots:
- Open a reliable online calculator, such as those available on Mathway, Symbolab, or Calculator-Online.net.
- Enter the expression you want to simplify into the calculator's input field. For example, if you want to simplify \(\sqrt{50}\), type "sqrt(50)" into the field.
- Click the "Calculate" or "Simplify" button to process the expression. The calculator will apply the appropriate mathematical rules to simplify the square root.
- Review the step-by-step solution provided by the calculator. This may include breaking down the number under the square root into its prime factors and simplifying accordingly.
Here are some examples to illustrate how online calculators work:
- Example 1: Simplifying \(\sqrt{75}\)
- Input: \(\sqrt{75}\)
- Step 1: Factor 75 into 25 and 3, i.e., \(75 = 25 \times 3\)
- Step 2: Simplify to \(5\sqrt{3}\)
- Output: \(5\sqrt{3}\)
- Example 2: Simplifying \(\sqrt{72}\)
- Input: \(\sqrt{72}\)
- Step 1: Factor 72 into 36 and 2, i.e., \(72 = 36 \times 2\)
- Step 2: Simplify to \(6\sqrt{2}\)
- Output: \(6\sqrt{2}\)
Online calculators can handle a variety of expressions, including those with multiple terms and different operations. They are especially useful for checking your work and ensuring accuracy in complex calculations.
Step-by-Step Examples
Below are detailed step-by-step examples to help you simplify radical expressions using various methods.
-
Example 1: Simplify \(\sqrt{50}\)
- Factor the number inside the square root: \(50 = 25 \times 2\).
- Write the square root of the product: \(\sqrt{50} = \sqrt{25 \times 2}\).
- Take the square root of the perfect square factor: \(\sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2}\).
- Simplify: \(\sqrt{25} = 5\), so \(\sqrt{50} = 5\sqrt{2}\).
-
Example 2: Simplify \(\sqrt{72}\)
- Factor the number inside the square root: \(72 = 36 \times 2\).
- Write the square root of the product: \(\sqrt{72} = \sqrt{36 \times 2}\).
- Take the square root of the perfect square factor: \(\sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2}\).
- Simplify: \(\sqrt{36} = 6\), so \(\sqrt{72} = 6\sqrt{2}\).
-
Example 3: Simplify \(\sqrt{32} + \sqrt{8}\)
- Factor the numbers inside the square roots: \(32 = 16 \times 2\) and \(8 = 4 \times 2\).
- Write the square roots of the products: \(\sqrt{32} = \sqrt{16 \times 2} = \sqrt{16} \times \sqrt{2}\) and \(\sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2}\).
- Simplify the square roots of the perfect square factors: \(\sqrt{16} = 4\) and \(\sqrt{4} = 2\).
- Combine the simplified terms: \( \sqrt{32} = 4\sqrt{2}\) and \(\sqrt{8} = 2\sqrt{2}\).
- Add the simplified terms: \(4\sqrt{2} + 2\sqrt{2} = 6\sqrt{2}\).
-
Example 4: Simplify \(\sqrt[3]{54}\)
- Factor the number inside the cube root: \(54 = 27 \times 2\).
- Write the cube root of the product: \(\sqrt[3]{54} = \sqrt[3]{27 \times 2}\).
- Take the cube root of the perfect cube factor: \(\sqrt[3]{27 \times 2} = \sqrt[3]{27} \times \sqrt[3]{2}\).
- Simplify: \(\sqrt[3]{27} = 3\), so \(\sqrt[3]{54} = 3\sqrt[3]{2}\).

Applications of Simplified Radicals
Simplified radicals find applications in various fields, particularly in mathematics, physics, engineering, and computer science. Below are some key applications:
-
Geometry:
Simplified radicals are used to express the lengths of sides and diagonals of geometric shapes. For example, the diagonal of a square with side length \(a\) is given by \(a\sqrt{2}\).
-
Physics:
In physics, simplified radicals appear in formulas related to wave mechanics, optics, and quantum physics. For example, the wavelength (\(\lambda\)) in the wave equation \(\lambda = \frac{hc}{E}\) often involves radicals when solving for energy levels.
-
Engineering:
Engineers use simplified radicals in calculations involving structural loads, electrical circuits, and material science. For instance, the resonant frequency of an LC circuit is given by \(f = \frac{1}{2\pi\sqrt{LC}}\).
-
Computer Science:
Simplified radicals are used in algorithms for computational geometry, graphics, and data analysis. Algorithms that involve distance calculations often use the Euclidean distance formula, which includes a square root: \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\).
-
Algebra:
Simplified radicals help in solving quadratic equations and inequalities. For example, the quadratic formula \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\) involves simplifying the radical expression under the square root.
Below are step-by-step examples demonstrating the application of simplified radicals in various problems:
-
Example in Geometry:
Find the length of the diagonal of a rectangle with sides 3 units and 4 units:
Using the Pythagorean theorem: \(d = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\)
-
Example in Physics:
Calculate the de Broglie wavelength of an electron with kinetic energy 150 eV:
\(\lambda = \frac{h}{\sqrt{2m_e E}} \approx \frac{6.626 \times 10^{-34}}{\sqrt{2 \times 9.109 \times 10^{-31} \times 150 \times 1.602 \times 10^{-19}}} \approx 1.01 \times 10^{-10} \, \text{m}\)
These examples illustrate how simplified radicals are integral to solving practical problems across different domains.
Frequently Asked Questions
-
What is a simplified radical expression?
A simplified radical expression is one in which the radicand (the number under the root) has no perfect square factors other than 1. The expression is reduced to its simplest form.
-
How do I simplify a square root expression?
To simplify a square root expression, you need to factor the radicand into its prime factors and then pair the factors. Each pair of factors can be taken out of the square root as a single factor.
For example, to simplify \( \sqrt{50} \):
- Factor 50 into prime factors: \( 50 = 2 \times 5 \times 5 \).
- Pair the 5s: \( \sqrt{50} = \sqrt{2 \times 5^2} \).
- Take the square root of the pair: \( \sqrt{2 \times 5^2} = 5\sqrt{2} \).
-
What is prime factorization, and how is it used to simplify radicals?Prime factorization is the process of breaking down a number into its prime factors. To simplify radicals, you use prime factorization to identify pairs of prime factors, which can then be taken out of the radical.
-
Can I use an online calculator to simplify radicals?
Yes, online calculators such as those from Symbolab, CalculatorSoup, and OmniCalculator can simplify radicals quickly. These calculators provide step-by-step solutions to help you understand the process.
-
How do I simplify a radical expression with variables?
The process is similar to simplifying numeric radicals. Factor the expression inside the radical, pair the factors, and simplify.
For example, to simplify \( \sqrt{18x^2y^3} \):
- Factor \( 18x^2y^3 \): \( 18 = 2 \times 3^2 \), \( x^2 \), \( y^3 = y^2 \times y \).
- Pair the factors: \( \sqrt{2 \times 3^2 \times x^2 \times y^2 \times y} \).
- Simplify: \( 3xy\sqrt{2y} \).
-
What are the rules for adding and subtracting radicals?You can only add or subtract radicals with the same radicand and index. For example, \( \sqrt{2} + 3\sqrt{2} = 4\sqrt{2} \), but \( \sqrt{2} + \sqrt{3} \) cannot be simplified further.
-
What are the rules for multiplying and dividing radicals?
When multiplying or dividing radicals, you can combine the radicands under a single radical sign.
For example, \( \sqrt{a} \times \sqrt{b} = \sqrt{ab} \) and \( \frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \).
Conclusion
Simplifying expressions with square roots is an essential skill in algebra that provides a solid foundation for tackling more complex mathematical problems. By mastering this process, you can transform complicated expressions into simpler forms, making them easier to work with and understand.
Throughout this guide, we've explored various methods for simplifying square roots, from basic rules and prime factorization to more complex techniques involving radical expressions. We've also discussed how to utilize online calculators to aid in the simplification process, ensuring accuracy and efficiency.
The applications of simplified radicals are numerous, ranging from solving equations in algebra and geometry to applications in physics and engineering. Simplified radicals are used to simplify measurements, solve quadratic equations, and even in calculating areas and volumes in geometric shapes.
We hope this comprehensive guide has provided you with the knowledge and tools needed to simplify square roots effectively. Whether you're a student, educator, or professional, these techniques will serve as valuable assets in your mathematical toolkit.
Remember, practice is key to mastering these concepts. Utilize online resources, practice problems, and step-by-step examples to reinforce your understanding and improve your skills.
Thank you for reading, and we wish you the best of luck in your mathematical endeavors!
Đơn giản hóa Biểu thức Căn bậc hai mà không cần Máy tính! | Hướng dẫn Từng bước
READ MORE:
Cách Đơn giản hóa Căn bậc hai











