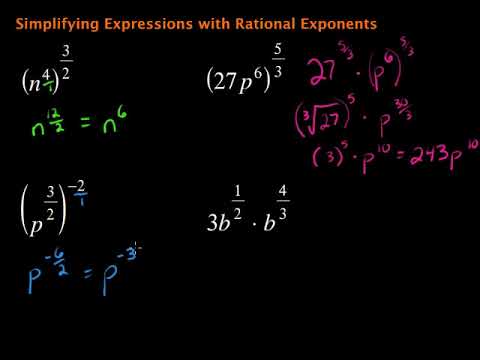Topic how do i simplify square roots: Simplifying square roots can seem challenging, but with the right approach, it becomes a straightforward process. This guide will walk you through the steps to simplify square roots, using clear examples and practical tips. Whether you're a student or just need a refresher, you'll find everything you need to master this essential math skill.
Table of Content
- How to Simplify Square Roots
- Introduction to Simplifying Square Roots
- Understanding Square Roots
- Basic Concepts of Simplifying Square Roots
- Prime Factorization Method
- Pairing Factors to Simplify Square Roots
- Simplifying Square Roots with Variables
- Examples of Simplifying Square Roots
- Common Mistakes to Avoid
- Advanced Techniques for Simplifying Square Roots
- Practical Applications of Simplifying Square Roots
- Practice Problems
- Tips and Tricks for Simplifying Square Roots
- Frequently Asked Questions (FAQs)
- Conclusion
- YOUTUBE:
How to Simplify Square Roots
Simplifying square roots involves breaking down a number into its prime factors and then simplifying by taking out pairs of factors. Here's a step-by-step guide to help you understand the process:
Steps to Simplify Square Roots
- Find the prime factors of the number inside the square root.
- Group the prime factors into pairs.
- Move each pair of prime factors outside the square root as a single number.
- If there are any remaining factors inside the square root, leave them inside.
Example: Simplifying \( \sqrt{72} \)
Let's break down \( \sqrt{72} \) step by step:
- Find the prime factors of 72: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
- Group the prime factors into pairs: \( (2 \times 2) \times (3 \times 3) \times 2 \).
- Move each pair outside the square root: \( 2 \times 3 \).
- Leave the remaining factor inside the square root: \( 2 \).
So, \( \sqrt{72} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \).
Example: Simplifying \( \sqrt{50} \)
Let's break down \( \sqrt{50} \) step by step:
- Find the prime factors of 50: \( 50 = 2 \times 5 \times 5 \).
- Group the prime factors into pairs: \( (5 \times 5) \times 2 \).
- Move the pair outside the square root: \( 5 \).
So, \( \sqrt{50} = 5 \sqrt{2} \).
Tips for Simplifying Square Roots
- Always look for the largest perfect square factor of the number inside the square root.
- If the number inside the square root is a perfect square, the square root is an integer.
- Practice with different numbers to get comfortable with the process.
By following these steps and tips, you can simplify any square root effectively.

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots is a fundamental skill in mathematics that involves reducing a square root to its simplest form. This process is essential for solving equations and understanding mathematical concepts more deeply. Here's a detailed, step-by-step guide to help you simplify square roots:
Step 1: Understand the Basics
A square root asks the question: "What number, when multiplied by itself, gives the original number?" For example, the square root of 9 is 3 because \(3 \times 3 = 9\).
Step 2: Prime Factorization
Break down the number inside the square root into its prime factors. Prime factors are the prime numbers that multiply together to give the original number.
- For example, the prime factors of 72 are \(2 \times 2 \times 2 \times 3 \times 3\).
Step 3: Group the Prime Factors
Group the prime factors into pairs. Each pair of prime factors can be taken out of the square root as a single number.
- For example, \(72 = 2 \times 2 \times 2 \times 3 \times 3\) can be grouped as \((2 \times 2) \times (3 \times 3) \times 2\).
Step 4: Simplify by Removing Pairs
Move each pair outside the square root. If there are any remaining factors inside the square root that do not form a pair, they stay inside.
- For example, \(\sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\).
By following these steps, you can simplify any square root. This skill is not only useful in solving mathematical problems but also in understanding more complex mathematical concepts.
Understanding Square Roots
A square root is a mathematical function that, given a number \( x \), finds a number \( y \) such that \( y^2 = x \). In other words, the square root of a number is a value that, when multiplied by itself, gives the original number.
Basic Properties of Square Roots
- Non-Negative Numbers: The square root of a non-negative number is always non-negative. For example, \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \).
- Zero: The square root of zero is zero, \( \sqrt{0} = 0 \), because \( 0 \times 0 = 0 \).
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are whole numbers.
Square Root Notation
The square root of a number is denoted using the radical symbol \( \sqrt{} \). For example, \( \sqrt{9} \) represents the square root of 9.
Principal Square Root
The principal square root is the non-negative square root of a number. When we refer to the square root of a number, we usually mean the principal square root. For example, \( \sqrt{16} = 4 \), not -4, even though \((-4) \times (-4) = 16\).
Square Roots of Non-Perfect Squares
When a number is not a perfect square, its square root is an irrational number. Irrational numbers cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal expansions. For example, \( \sqrt{2} \) is approximately 1.414, but it cannot be written exactly as a fraction.
Examples of Square Roots
- \(\sqrt{4} = 2\) because \(2 \times 2 = 4\).
- \(\sqrt{9} = 3\) because \(3 \times 3 = 9\).
- \(\sqrt{25} = 5\) because \(5 \times 5 = 25\).
- \(\sqrt{10}\) is approximately 3.162, as 10 is not a perfect square.
Understanding square roots is crucial for simplifying them and solving various mathematical problems. Mastering this concept will help you in algebra, geometry, and beyond.
Basic Concepts of Simplifying Square Roots
Simplifying square roots involves reducing a square root to its simplest form. This process makes it easier to work with square roots in mathematical expressions and equations. Here are the basic concepts to understand:
Step 1: Identifying Perfect Squares
A perfect square is a number that is the square of an integer. For example, 1, 4, 9, 16, and 25 are perfect squares because they are \(1^2, 2^2, 3^2, 4^2,\) and \(5^2\), respectively.
Step 2: Prime Factorization
Prime factorization involves breaking down a number into its prime factors, which are prime numbers that multiply together to give the original number. For example, the prime factors of 18 are \(2 \times 3 \times 3\).
Step 3: Grouping Prime Factors
To simplify a square root, group the prime factors into pairs. Each pair of prime factors can be taken out of the square root as a single number. For example:
- \(\sqrt{72} = \sqrt{2 \times 2 \times 2 \times 3 \times 3} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\)
Step 4: Simplifying Non-Perfect Squares
When the number inside the square root is not a perfect square, simplify by taking out pairs and leaving the remaining factors inside the square root. For example:
- \(\sqrt{50} = \sqrt{2 \times 5 \times 5} = \sqrt{(5 \times 5) \times 2} = 5\sqrt{2}\)
Step 5: Combining Like Terms
When working with multiple square roots, combine like terms to simplify the expression further. For example:
- \(2\sqrt{3} + 3\sqrt{3} = (2 + 3)\sqrt{3} = 5\sqrt{3}\)
Examples of Simplifying Square Roots
- \(\sqrt{36} = 6\) because \(6 \times 6 = 36\).
- \(\sqrt{45} = \sqrt{9 \times 5} = 3\sqrt{5}\).
- \(\sqrt{98} = \sqrt{49 \times 2} = 7\sqrt{2}\).
By understanding and applying these basic concepts, you can simplify any square root and make complex mathematical problems more manageable.
Prime Factorization Method
The Prime Factorization Method is an effective way to simplify square roots by breaking down the number inside the square root into its prime factors. This method helps in identifying perfect square factors that can be simplified. Here's a step-by-step guide to using the Prime Factorization Method:
- Find the Prime Factors
Prime factorization involves expressing the number inside the square root as a product of its prime factors. Prime factors are prime numbers that multiply together to give the original number.
- Example: The prime factors of 72 are \(2 \times 2 \times 2 \times 3 \times 3\).
- Group the Prime Factors into Pairs
Next, group the prime factors into pairs. Each pair of prime factors can be taken out of the square root as a single number.
- Example: \(72 = 2 \times 2 \times 2 \times 3 \times 3\) can be grouped as \((2 \times 2) \times (3 \times 3) \times 2\).
- Simplify by Moving Pairs Outside the Square Root
Move each pair of prime factors outside the square root. Any remaining factors that do not form a pair will stay inside the square root.
- Example: \(\sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\).
Let's look at a few more examples to understand this method better:
- Example 1: Simplify \(\sqrt{50}\)
- Find prime factors: \(50 = 2 \times 5 \times 5\).
- Group into pairs: \((5 \times 5) \times 2\).
- Move pairs outside: \(5\sqrt{2}\).
- Simplified form: \(\sqrt{50} = 5\sqrt{2}\).
- Example 2: Simplify \(\sqrt{45}\)
- Find prime factors: \(45 = 3 \times 3 \times 5\).
- Group into pairs: \((3 \times 3) \times 5\).
- Move pairs outside: \(3\sqrt{5}\).
- Simplified form: \(\sqrt{45} = 3\sqrt{5}\).
- Example 3: Simplify \(\sqrt{18}\)
- Find prime factors: \(18 = 2 \times 3 \times 3\).
- Group into pairs: \((3 \times 3) \times 2\).
- Move pairs outside: \(3\sqrt{2}\).
- Simplified form: \(\sqrt{18} = 3\sqrt{2}\).
By mastering the Prime Factorization Method, you can simplify square roots efficiently and accurately, making complex mathematical problems more manageable.
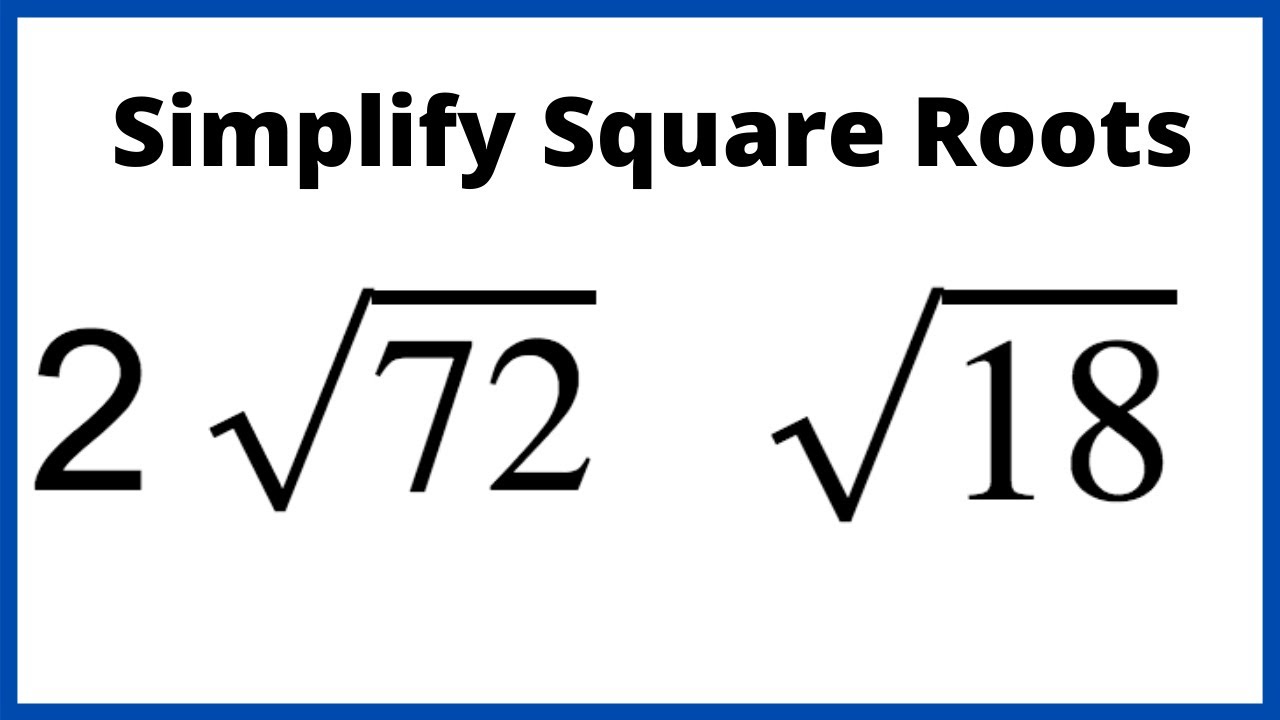
Pairing Factors to Simplify Square Roots
Pairing factors is a critical step in simplifying square roots. By identifying pairs of factors, you can extract these pairs from under the square root, simplifying the expression. Here’s a detailed, step-by-step guide to help you through this process:
- Find the Prime Factors
Break down the number inside the square root into its prime factors. Prime factors are prime numbers that multiply together to give the original number.
- Example: The prime factors of 72 are \(2 \times 2 \times 2 \times 3 \times 3\).
- Group the Prime Factors into Pairs
Group the prime factors into pairs. Each pair of prime factors can be taken out of the square root as a single number.
- Example: \(72 = 2 \times 2 \times 2 \times 3 \times 3\) can be grouped as \((2 \times 2) \times (3 \times 3) \times 2\).
- Simplify by Moving Pairs Outside the Square Root
Move each pair of prime factors outside the square root. Any remaining factors that do not form a pair will stay inside the square root.
- Example: \(\sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\).
Let’s apply this method to a few more examples:
- Example 1: Simplify \(\sqrt{50}\)
- Find prime factors: \(50 = 2 \times 5 \times 5\).
- Group into pairs: \((5 \times 5) \times 2\).
- Move pairs outside: \(5\sqrt{2}\).
- Simplified form: \(\sqrt{50} = 5\sqrt{2}\).
- Example 2: Simplify \(\sqrt{45}\)
- Find prime factors: \(45 = 3 \times 3 \times 5\).
- Group into pairs: \((3 \times 3) \times 5\).
- Move pairs outside: \(3\sqrt{5}\).
- Simplified form: \(\sqrt{45} = 3\sqrt{5}\).
- Example 3: Simplify \(\sqrt{18}\)
- Find prime factors: \(18 = 2 \times 3 \times 3\).
- Group into pairs: \((3 \times 3) \times 2\).
- Move pairs outside: \(3\sqrt{2}\).
- Simplified form: \(\sqrt{18} = 3\sqrt{2}\).
By mastering the technique of pairing factors, you can simplify square roots efficiently and accurately, making it easier to work with them in various mathematical problems.
Simplifying Square Roots with Variables
Simplifying square roots that contain variables follows the same principles as simplifying numerical square roots. The key is to factor the expression under the square root into products of squares and non-squares. Here are the steps to simplify square roots with variables:
- Identify and separate the numerical and variable components.
- Factor each component into its prime factors or powers.
- Group the factors into pairs of identical factors (for variables, pair the exponents as even numbers).
- Take the square root of each pair, moving them outside the radical.
- Simplify the remaining expression under the radical, if any.
Let's look at some examples to illustrate these steps:
Example 1: Simplifying a Single Variable
Simplify \( \sqrt{x^6} \).
Solution:
- Rewrite the variable as a product of squares: \( x^6 = (x^3)^2 \).
- Take the square root: \( \sqrt{(x^3)^2} = x^3 \).
Therefore, \( \sqrt{x^6} = x^3 \).
Example 2: Simplifying Multiple Variables
Simplify \( \sqrt{w \cdot x^9 \cdot y^8 \cdot z^5} \).
Solution:
- Rewrite the variables to factor out squares:
- \( x^9 = (x^4)^2 \cdot x \)
- \( y^8 = (y^4)^2 \)
- \( z^5 = (z^2)^2 \cdot z \)
- Combine the factors: \( w \cdot x^9 \cdot y^8 \cdot z^5 = w \cdot (x^4)^2 \cdot x \cdot (y^4)^2 \cdot (z^2)^2 \cdot z \).
- Take the square root of each square: \( \sqrt{w \cdot (x^4)^2 \cdot x \cdot (y^4)^2 \cdot (z^2)^2 \cdot z} = x^4 \cdot y^4 \cdot z^2 \cdot \sqrt{w \cdot x \cdot z} \).
Therefore, \( \sqrt{w \cdot x^9 \cdot y^8 \cdot z^5} = x^4 \cdot y^4 \cdot z^2 \cdot \sqrt{w \cdot x \cdot z} \).
Example 3: Simplifying with Coefficients
Simplify \( \sqrt{12x^5y^2} \).
Solution:
- Factor the numerical part: \( 12 = 2^2 \cdot 3 \).
- Rewrite the variable parts to factor out squares:
- \( x^5 = (x^2)^2 \cdot x \)
- \( y^2 = (y)^2 \)
- Combine the factors: \( \sqrt{12x^5y^2} = \sqrt{2^2 \cdot 3 \cdot (x^2)^2 \cdot x \cdot (y)^2} \).
- Take the square root of each square: \( 2x^2y \cdot \sqrt{3x} \).
Therefore, \( \sqrt{12x^5y^2} = 2x^2y \cdot \sqrt{3x} \).
By following these steps, you can simplify any square root expression containing variables, making it easier to work with in various mathematical applications.
Examples of Simplifying Square Roots
Simplifying square roots involves reducing the square root to its simplest form. Here are some detailed examples:
Example 1: Simplify √50
- Factor the number inside the square root: 50 = 25 × 2
- Rewrite the square root using the product rule: √50 = √(25 × 2)
- Split the square root: √50 = √25 × √2
- Simplify the square roots: √25 = 5 and √2 remains the same
- Combine the results: √50 = 5√2
Example 2: Simplify √72
- Factor the number inside the square root: 72 = 36 × 2
- Rewrite the square root using the product rule: √72 = √(36 × 2)
- Split the square root: √72 = √36 × √2
- Simplify the square roots: √36 = 6 and √2 remains the same
- Combine the results: √72 = 6√2
Example 3: Simplify √200
- Factor the number inside the square root: 200 = 100 × 2
- Rewrite the square root using the product rule: √200 = √(100 × 2)
- Split the square root: √200 = √100 × √2
- Simplify the square roots: √100 = 10 and √2 remains the same
- Combine the results: √200 = 10√2
Example 4: Simplify √72a2b4
- Factor the number and variables inside the square root: 72a2b4 = 36 × 2 × a2 × b4
- Rewrite the square root using the product rule: √(36 × 2 × a2 × b4)
- Split the square root: √36 × √2 × √a2 × √b4
- Simplify the square roots: √36 = 6, √a2 = a, and √b4 = b2
- Combine the results: √72a2b4 = 6ab2√2
Example 5: Simplify 2√18 + 3√8
- Simplify each square root individually:
- √18 = √(9 × 2) = √9 × √2 = 3√2
- √8 = √(4 × 2) = √4 × √2 = 2√2
- Combine like terms: 2√18 + 3√8 = 2(3√2) + 3(2√2) = 6√2 + 6√2
- Combine the coefficients: 6√2 + 6√2 = 12√2
By following these steps and practicing with different numbers, you can become proficient at simplifying square roots.
Common Mistakes to Avoid
While simplifying square roots, it's important to be aware of common mistakes that can lead to incorrect results. Here are some key mistakes to avoid:
- Overlooking Perfect Squares: Always check for perfect squares within the radicand. For example, in , recognizing that 50 can be broken down into 25 and 2 allows simplification to .
- Misapplying Properties: Ensure correct application of the product and quotient properties of square roots. Remember, is , but is not equal to .
- Ignoring Variables: When variables are involved, identify and simplify any that are perfect squares. For example, simplifies to .
- Simplification Errors: Double-check factorization and arithmetic operations. Incorrect factorization or simplification steps can lead to errors.
- Forgetting to Rationalize the Denominator: Leaving a square root in the denominator is often considered incomplete. For example, should be rationalized to .
Avoiding these common mistakes will improve your accuracy and efficiency in simplifying square roots. Practice regularly and verify each step to ensure correct simplification.

Advanced Techniques for Simplifying Square Roots
Mastering advanced techniques for simplifying square roots can greatly enhance your mathematical skills, especially when dealing with more complex expressions. Below are detailed methods and steps to handle these advanced simplifications.
Using the Quotient Property
The quotient property of square roots allows you to simplify the square root of a fraction by dealing with the numerator and denominator separately.
- Identify the numerator and denominator inside the square root. For example, simplify \( \sqrt{\frac{4}{9}} \).
- Apply the quotient property: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). Thus, \( \sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} \).
- Simplify the square roots individually: \( \frac{\sqrt{4}}{\sqrt{9}} = \frac{2}{3} \).
Rationalizing the Denominator
Rationalizing the denominator involves eliminating the square root from the denominator of a fraction. This process is essential for simplifying and standardizing expressions.
- Identify the radical in the denominator. For example, simplify \( \frac{1}{\sqrt{2}} \).
- Multiply the numerator and denominator by the same radical to eliminate the square root in the denominator: \( \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \).
Simplifying Radicals with Variables
When variables are involved, apply the same principles used for numerical square roots, with careful attention to the properties of exponents.
- Factor the expression under the square root, identifying perfect square factors. For example, simplify \( \sqrt{x^4y^3} \).
- Apply the product property: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \). Thus, \( \sqrt{x^4 \cdot y^3} = \sqrt{x^4} \cdot \sqrt{y^3} \).
- Simplify each part separately: \( \sqrt{x^4} = x^2 \) and \( \sqrt{y^3} = y^{3/2} \). Combine the results: \( x^2 \cdot y^{3/2} \).
Using Conjugates
For expressions with binomial denominators involving square roots, use conjugates to simplify.
- Identify the conjugate of the denominator. For example, simplify \( \frac{5}{2 + \sqrt{3}} \).
- Multiply the numerator and the denominator by the conjugate of the denominator: \( \frac{5}{2 + \sqrt{3}} \times \frac{2 - \sqrt{3}}{2 - \sqrt{3}} = \frac{5(2 - \sqrt{3})}{(2 + \sqrt{3})(2 - \sqrt{3})} \).
- Simplify the result: \( \frac{10 - 5\sqrt{3}}{4 - 3} = 10 - 5\sqrt{3} \).
Prime Factorization
Prime factorization helps simplify radicals by breaking down the number into its prime factors.
- Factorize the number into primes. For example, simplify \( \sqrt{72} \).
- Prime factors of 72 are \( 2^3 \cdot 3^2 \).
- Group the prime factors into pairs: \( \sqrt{72} = \sqrt{(2^2 \cdot 3^2) \cdot 2} = 6\sqrt{2} \).
By mastering these advanced techniques, you can simplify complex square root expressions efficiently, enhancing your problem-solving capabilities in algebra and beyond.
Practical Applications of Simplifying Square Roots
Simplifying square roots is not just an academic exercise; it has many practical applications in various fields. Here are some examples:
1. Geometry and Construction
In geometry, the distance between two points in a plane or in space can be found using the distance formula, which involves square roots.
- The distance \( D \) between points \((x_1, y_1)\) and \((x_2, y_2)\) in 2D space is calculated as:
- In 3D space, the distance formula extends to:
\[ D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
\[ D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \]
2. Physics and Engineering
Square roots are used in physics, particularly in equations related to motion and gravity.
- For example, the time \( t \) it takes for an object to fall from a height \( h \) is given by:
\[ t = \frac{\sqrt{h}}{4} \]
3. Medicine
In medical imaging, such as MRI and CT scans, square roots are used in algorithms that reconstruct images from raw data.
4. Finance
In finance, square roots are involved in calculating standard deviation and variance, which are measures of risk and volatility in investments.
5. Accident Investigation
Police use square roots to determine the speed of a vehicle before a crash based on the length of skid marks.
- The speed \( s \) in miles per hour can be estimated using:
- where \( d \) is the length of the skid marks in feet.
\[ s = \sqrt{24d} \]
6. Architecture
In architecture, square roots help in calculating the diagonal lengths of squares and rectangles, ensuring structures are built accurately.
7. Environmental Science
Square roots are used in calculating the root mean square error (RMSE) in environmental data modeling, which measures the differences between predicted and observed values.
Understanding these practical applications highlights the importance of being able to simplify square roots efficiently and accurately.
Practice Problems
Here are some practice problems to help you master the process of simplifying square roots. Work through these problems step-by-step, ensuring that you follow the correct methods to simplify each expression. Use the hints provided if you get stuck.
- Problem 1: Simplify \( \sqrt{50} \)
- Problem 2: Simplify \( \sqrt{72} \)
- Problem 3: Simplify \( \sqrt{98} \)
- Problem 4: Simplify \( \sqrt{200} \)
- Problem 5: Simplify \( \sqrt{45} \)
- Problem 6: Simplify \( \sqrt{32} \)
- Problem 7: Simplify \( \sqrt{18} \)
Hint: Break down 50 into its prime factors and look for pairs.
Solution: \( \sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2} \)
Hint: Decompose 72 into its prime factors and simplify.
Solution: \( \sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2} \)
Hint: Find the largest perfect square factor of 98.
Solution: \( \sqrt{98} = \sqrt{49 \cdot 2} = \sqrt{49} \cdot \sqrt{2} = 7\sqrt{2} \)
Hint: Identify the perfect squares within 200.
Solution: \( \sqrt{200} = \sqrt{100 \cdot 2} = \sqrt{100} \cdot \sqrt{2} = 10\sqrt{2} \)
Hint: Break down 45 into prime factors.
Solution: \( \sqrt{45} = \sqrt{9 \cdot 5} = \sqrt{9} \cdot \sqrt{5} = 3\sqrt{5} \)
Hint: Decompose 32 into its prime factors and simplify.
Solution: \( \sqrt{32} = \sqrt{16 \cdot 2} = \sqrt{16} \cdot \sqrt{2} = 4\sqrt{2} \)
Hint: Find the perfect square factors within 18.
Solution: \( \sqrt{18} = \sqrt{9 \cdot 2} = \sqrt{9} \cdot \sqrt{2} = 3\sqrt{2} \)
Practice these problems multiple times until you feel confident with the process of simplifying square roots. Remember, the key is to break down the number inside the square root into its prime factors and simplify by removing any perfect squares.
Tips and Tricks for Simplifying Square Roots
Simplifying square roots can be made easier with some useful tips and tricks. Here are some steps and strategies to help you master this process:
- Recognize Perfect Squares: Memorize the list of perfect squares (e.g., \(1, 4, 9, 16, 25, 36, 49, 64, 81, 100\)). This helps in identifying factors quickly.
- Prime Factorization: Break down the number inside the square root into its prime factors. For example, \( \sqrt{72} \) can be broken down into \( \sqrt{2^3 \cdot 3^2} \).
- Pairing Factors: When you have pairs of prime factors, take one factor out of the square root. For instance, \( \sqrt{2^3 \cdot 3^2} = \sqrt{2^2 \cdot 2 \cdot 3^2} = 2 \cdot 3 \cdot \sqrt{2} = 6\sqrt{2} \).
- Using the Product Property: The product property of square roots states that \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \). This can simplify calculations. For example, \( \sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2} \).
- Dividing and Simplifying: For more complex numbers, divide them by the largest perfect square. For example, \( \sqrt{200} = \sqrt{100 \cdot 2} = 10\sqrt{2} \).
- Simplifying with Variables: Apply the same principles when variables are involved. For example, \( \sqrt{50x^2} = \sqrt{25 \cdot 2 \cdot x^2} = 5x\sqrt{2} \).
- Estimation: When exact simplification isn't possible, use estimation. For example, \( \sqrt{45} \approx \sqrt{36 + 9} = 6 + 3 = 9 \), then refine the estimate.
By practicing these tips and tricks, you can improve your ability to simplify square roots quickly and accurately.

Frequently Asked Questions (FAQs)
-
Q1: What is the basic process for simplifying square roots?
A: To simplify a square root, factor the number into its prime factors, pair the prime factors, and then move each pair out of the square root.
Example: Simplify \(\sqrt{18}\).
- Factor 18 into primes: \(18 = 2 \times 3 \times 3\).
- Pair the prime factors: \(18 = 2 \times (3 \times 3)\).
- Move the pair out of the square root: \(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\).
-
Q2: How do I simplify square roots of fractions?
A: Simplify the numerator and the denominator separately, then divide.
Example: Simplify \(\sqrt{\frac{25}{9}}\).
- Simplify the numerator: \(\sqrt{25} = 5\).
- Simplify the denominator: \(\sqrt{9} = 3\).
- Divide the simplified results: \(\sqrt{\frac{25}{9}} = \frac{5}{3}\).
-
Q3: How can I simplify square roots with variables?
A: Apply the same process of factoring and pairing to the coefficients and the variables.
Example: Simplify \(\sqrt{50x^4}\).
- Factor the coefficient: \(50 = 2 \times 5^2\).
- Factor the variable: \(x^4 = (x^2)^2\).
- Pair the factors: \(\sqrt{50x^4} = \sqrt{2 \times 5^2 \times (x^2)^2}\).
- Move pairs out of the square root: \(5x^2\sqrt{2}\).
-
Q4: Can all square roots be simplified?
A: No, some square roots cannot be simplified if the number inside the square root does not have any perfect square factors other than 1. These are called surds.
Example: \(\sqrt{3}\) is a surd because 3 has no perfect square factors other than 1.
-
Q5: What are some common mistakes to avoid when simplifying square roots?
- Forgetting to pair all prime factors.
- Not simplifying both the numerator and the denominator in a fraction.
- Ignoring the presence of variables or not correctly factoring them.
Conclusion
Simplifying square roots is an essential skill in mathematics that helps in various areas such as algebra, geometry, and calculus. By breaking down complex square roots into simpler forms, we can make calculations easier and more efficient. Here are the key takeaways:
- Understanding Square Roots: A square root of a number is a value that, when multiplied by itself, gives the original number.
- Prime Factorization Method: This involves expressing the number inside the square root as a product of prime factors and then simplifying.
- Pairing Factors: Identify pairs of factors and bring them out of the square root to simplify the expression.
- Simplifying with Variables: Apply the same principles to expressions containing variables, ensuring to consider the exponents and variable properties.
- Common Mistakes: Avoid errors such as forgetting to simplify completely or mishandling variables.
- Advanced Techniques: These include simplifying complex fractions and radicals, often using rationalization techniques.
By mastering these methods, you can approach more complex mathematical problems with confidence. Practice regularly, review your steps, and use these techniques to simplify square roots effectively. Remember, mathematics is a skill that improves with practice and perseverance.
We hope this guide has provided you with a comprehensive understanding of how to simplify square roots. Keep practicing, and soon you'll find these techniques becoming second nature.
Cách Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Hướng dẫn cách đơn giản hóa căn bậc hai một cách dễ hiểu và chi tiết với Thầy J.
Đơn Giản Hóa Căn Bậc Hai | Toán học với Thầy J