Topic how do you simplify a negative square root: Learn how to simplify a negative square root with our comprehensive guide. Understanding this essential mathematical concept can be straightforward and rewarding. Discover step-by-step instructions and practical examples that make simplifying negative square roots easy and intuitive.
Table of Content
- How to Simplify a Negative Square Root
- Introduction to Simplifying Negative Square Roots
- Understanding Imaginary Numbers
- Steps to Simplify the Square Root of a Negative Number
- Examples of Simplifying Negative Square Roots
- Common Mistakes and How to Avoid Them
- Practice Problems and Solutions
- Applications of Imaginary Numbers
- Further Reading and Resources
- YOUTUBE:
How to Simplify a Negative Square Root
To simplify a negative square root, follow these steps:
- Identify the negative sign before the square root.
- Apply the property of square roots that states \( \sqrt{-a} = i\sqrt{a} \), where \( i \) is the imaginary unit.
- If the expression under the square root is a perfect square, simplify it as usual and multiply by \( i \).
- Ensure the final answer is in the form \( i\sqrt{b} \), where \( b \) is a positive number.
For example, to simplify \( \sqrt{-25} \):
| Step 1: | Identify the negative sign. |
| Step 2: | Apply \( \sqrt{-25} = i\sqrt{25} = 5i \). |

READ MORE:
Introduction to Simplifying Negative Square Roots
When simplifying the square root of a negative number, the process involves the concept of imaginary numbers. This is because there is no real number that can be squared to produce a negative result. Instead, we use the imaginary unit, denoted as \(i\), which is defined as the square root of -1.
Here is a step-by-step guide to simplifying negative square roots:
-
Recognize the imaginary unit \(i\):
The imaginary unit \(i\) is defined as \(i = \sqrt{-1}\). This fundamental concept allows us to handle the square roots of negative numbers.
-
Express the negative square root using \(i\):
Rewrite the square root of a negative number in terms of \(i\). For example, \(\sqrt{-16}\) can be written as \(\sqrt{16 \cdot -1}\).
-
Simplify the positive part:
Separate the square root into the product of the square roots of the positive part and \(-1\). Using the previous example, \(\sqrt{16 \cdot -1}\) becomes \(\sqrt{16} \cdot \sqrt{-1}\).
-
Apply the imaginary unit:
Substitute \(i\) for \(\sqrt{-1}\). Continuing the example, \(\sqrt{16} \cdot \sqrt{-1}\) becomes \(4i\) since \(\sqrt{16} = 4\) and \(\sqrt{-1} = i\).
Therefore, the simplified form of \(\sqrt{-16}\) is \(4i\). This method applies to any negative square root, allowing us to work with these numbers within the realm of complex numbers.
Understanding Imaginary Numbers
Imaginary numbers are a fundamental concept in mathematics, essential for solving problems involving the square root of negative numbers. When mathematicians encountered the square root of a negative number, they created a new number, i, defined as the square root of -1. This new number allows for the extension of the real number system to include solutions to equations that previously had no solutions within the reals.
The imaginary unit i has the unique property that i2 = -1. This property enables the simplification of negative square roots.
Properties of Imaginary Numbers
- Definition: i = √(-1)
- Properties:
- i2 = -1
- i3 = -i
- i4 = 1
Using Imaginary Numbers to Simplify Negative Square Roots
To simplify the square root of a negative number, we follow these steps:
- Express the negative number as the product of -1 and a positive number.
- Separate the square root into two parts: the square root of -1 and the square root of the positive number.
- Replace the square root of -1 with i.
For example, to simplify √(-16):
| Step 1: | √(-16) = √(-1 * 16) |
| Step 2: | √(-1) * √(16) |
| Step 3: | i * 4 |
| Result: | 4i |
This process shows how imaginary numbers allow us to work with square roots of negative numbers, enabling solutions to previously unsolvable equations and expanding our mathematical toolkit.
Steps to Simplify the Square Root of a Negative Number
When simplifying the square root of a negative number, you need to use the imaginary unit i, where i is defined as i = \sqrt{-1}. The steps below outline how to simplify such square roots:
-
Identify the negative sign under the square root.
For example, consider
\(\sqrt{-a}\). -
Rewrite the square root of the negative number as the product of the square root of -1 and the square root of the positive counterpart.
Example:
\(\sqrt{-a} = \sqrt{-1 \cdot a}\). -
Express the square root of -1 as i.
Example:
\(\sqrt{-a} = \sqrt{-1} \cdot \sqrt{a} = i \cdot \sqrt{a}\). -
Simplify the expression if possible.
Example:
\(i \cdot \sqrt{a}\). Ifacan be further simplified, do so.
Let's go through some examples:
| Example | Steps | Result |
|---|---|---|
\(\sqrt{-9}\) |
|
3i |
\(\sqrt{-50}\) |
|
5i\sqrt{2} |
Examples of Simplifying Negative Square Roots
Let's go through some examples to understand how to simplify the square roots of negative numbers. Remember, when dealing with negative square roots, we introduce the imaginary unit \(i\), where \(i = \sqrt{-1}\).
Example 1: Simplify \(\sqrt{-25}\)
- Identify the negative sign and the number under the square root: \(\sqrt{-25}\).
- Separate the negative sign and the number: \(\sqrt{-1 \times 25}\).
- Use the property of square roots to split them: \(\sqrt{-1} \times \sqrt{25}\).
- Substitute \(\sqrt{-1}\) with \(i\): \(i \times \sqrt{25}\).
- Simplify \(\sqrt{25}\) to 5: \(i \times 5\) or \(5i\).
The simplified form of \(\sqrt{-25}\) is \(5i\).
Example 2: Simplify \(\sqrt{-8}\)
- Identify the negative sign and the number under the square root: \(\sqrt{-8}\).
- Separate the negative sign and the number: \(\sqrt{-1 \times 8}\).
- Use the property of square roots to split them: \(\sqrt{-1} \times \sqrt{8}\).
- Substitute \(\sqrt{-1}\) with \(i\): \(i \times \sqrt{8}\).
- Simplify \(\sqrt{8}\) to \(2\sqrt{2}\): \(i \times 2\sqrt{2}\) or \(2i\sqrt{2}\).
The simplified form of \(\sqrt{-8}\) is \(2i\sqrt{2}\).
Example 3: Simplify \(\sqrt{-50}\)
- Identify the negative sign and the number under the square root: \(\sqrt{-50}\).
- Separate the negative sign and the number: \(\sqrt{-1 \times 50}\).
- Use the property of square roots to split them: \(\sqrt{-1} \times \sqrt{50}\).
- Substitute \(\sqrt{-1}\) with \(i\): \(i \times \sqrt{50}\).
- Simplify \(\sqrt{50}\) to \(5\sqrt{2}\): \(i \times 5\sqrt{2}\) or \(5i\sqrt{2}\).
The simplified form of \(\sqrt{-50}\) is \(5i\sqrt{2}\).

Common Mistakes and How to Avoid Them
When simplifying negative square roots, it’s essential to be aware of common mistakes and misconceptions. Here are some frequent errors and tips on how to avoid them:
- Forgetting the Imaginary Unit:
One of the most common mistakes is forgetting to include the imaginary unit \( i \) when simplifying the square root of a negative number. Always remember that the square root of a negative number involves \( i \), where \( i^2 = -1 \).
- Incorrect Sign of the Imaginary Unit:
Another common error is getting the sign of the imaginary unit wrong. The square root of a negative number is not a negative real number. For example, \( \sqrt{-4} \) is \( 2i \), not \(-2\).
- Overcomplicating the Process:
Sometimes, students overcomplicate the simplification process. Simplifying negative square roots can be straightforward if you first convert the negative under the square root to its positive counterpart and then apply the imaginary unit \( i \). For instance, \( \sqrt{-16} = \sqrt{16} \cdot i = 4i \).
- Misconception About Usefulness:
There is a misconception that imaginary numbers are not useful in real-life situations. In reality, imaginary numbers are crucial in fields such as engineering, physics, and electronics. They are used to solve problems involving complex numbers, such as in AC circuit analysis.
By understanding and avoiding these common mistakes, you can simplify negative square roots accurately and with confidence.
Practice Problems and Solutions
Below are some practice problems to help you master simplifying negative square roots. Each problem is followed by a detailed solution.
-
Simplify \( \sqrt{-5} \)
Solution:
- Rewrite the square root of the negative number using \(i\):
- Simplify the square root of \(-1\) to \(i\):
- Combine the results:
\( \sqrt{-5} = \sqrt{-1 \cdot 5} = \sqrt{-1} \cdot \sqrt{5} \)
\( \sqrt{-1} = i \)
\( \sqrt{-5} = i\sqrt{5} \)
-
Simplify \( \sqrt{-36} \)
Solution:
- Rewrite the square root of the negative number using \(i\):
- Simplify the square root of \(-1\) to \(i\) and the square root of 36:
- Combine the results:
\( \sqrt{-36} = \sqrt{-1 \cdot 36} = \sqrt{-1} \cdot \sqrt{36} \)
\( \sqrt{-1} = i \) and \( \sqrt{36} = 6 \)
\( \sqrt{-36} = i \cdot 6 = 6i \)
-
Simplify \( \sqrt{-48} \)
Solution:
- Rewrite the square root of the negative number using \(i\):
- Simplify the square root of \(-1\) to \(i\) and factor the radicand:
- Combine the results:
\( \sqrt{-48} = \sqrt{-1 \cdot 48} = \sqrt{-1} \cdot \sqrt{48} \)
\( \sqrt{-1} = i \) and \( \sqrt{48} = \sqrt{16 \cdot 3} = \sqrt{16} \cdot \sqrt{3} = 4\sqrt{3} \)
\( \sqrt{-48} = i \cdot 4\sqrt{3} = 4i\sqrt{3} \)
-
Simplify \( \sqrt{-50} \)
Solution:
- Rewrite the square root of the negative number using \(i\):
- Simplify the square root of \(-1\) to \(i\) and factor the radicand:
- Combine the results:
\( \sqrt{-50} = \sqrt{-1 \cdot 50} = \sqrt{-1} \cdot \sqrt{50} \)
\( \sqrt{-1} = i \) and \( \sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2} \)
\( \sqrt{-50} = i \cdot 5\sqrt{2} = 5i\sqrt{2} \)
Applications of Imaginary Numbers
Imaginary numbers, represented by the unit \( i \) where \( i = \sqrt{-1} \), have numerous practical applications in various fields. Here are some key applications:
-
Electrical Engineering:
Imaginary numbers are used to analyze and design electrical circuits, particularly in AC circuit analysis. The impedance of a circuit is often expressed as a complex number \( Z = R + jX \), where \( R \) is the resistance, \( X \) is the reactance, and \( j \) is the imaginary unit.
Example: Calculate the impedance \( Z \) for a circuit with \( R = 3 \Omega \) and \( X = 4 \Omega \): Solution: \( Z = 3 + 4i \) -
Signal Processing:
Imaginary numbers are essential in signal processing, including Fourier transforms. They help decompose signals into their frequency components, making it easier to analyze and manipulate these signals.
For example, the Fourier transform uses the complex exponential \( e^{i\omega t} \) to convert time-domain signals into the frequency domain.
-
Control Systems:
Control engineers use imaginary numbers for stability analysis of control systems. The poles of a system's transfer function, which determine stability, are often complex numbers.
-
Quantum Mechanics:
In physics, imaginary numbers are used in the Schrödinger equation to describe the wave function of quantum systems. The equation involves the imaginary unit to account for the probabilistic nature of quantum mechanics.
-
Fractals:
Imaginary numbers are used to generate fractals, such as the Mandelbrot set. These sets are visual representations of complex numbers and are used in various fields, including computer graphics and natural phenomena modeling.
These applications demonstrate the importance of imaginary numbers in both theoretical and practical aspects of science and engineering.
Further Reading and Resources
To deepen your understanding of simplifying negative square roots and the applications of imaginary numbers, here are some recommended readings and resources:
-
Understanding Imaginary Numbers
- - This tutorial provides a comprehensive overview of simplifying negative square roots.
-
Practice Problems and Solutions
- - Offers interactive calculators, video tutorials, and practice problems to reinforce your learning.
- - An excellent resource for solving and simplifying square roots, including step-by-step explanations.
-
Advanced Concepts
- - Explore more advanced topics related to complex numbers and their properties.
- - A comprehensive guide to understanding complex numbers, including their applications in various fields.
-
Further Exploration
- - Simplified explanations and interactive content to make learning about complex numbers enjoyable.
- - Detailed lessons on complex numbers, including operations and properties.
These resources will help you gain a deeper understanding of the topic and provide ample practice to master simplifying negative square roots and working with imaginary numbers.
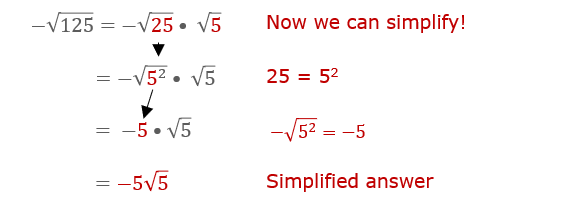
Đại số 2 - Đơn giản hóa căn bậc hai âm bằng đơn vị tưởng tượng i, sqrt(-24)
READ MORE:
Cách Tìm Căn Bậc Hai Của Một Số Âm










