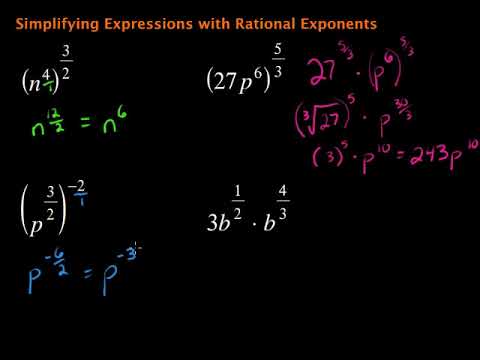Topic how do i simplify a square root: Learning how to simplify a square root can transform complex mathematical expressions into manageable forms. In this guide, we'll explore essential techniques and rules for simplifying square roots, providing you with clear, step-by-step instructions and practical examples. Simplifying square roots is easier than you think, and with practice, you'll master this fundamental math skill in no time!
Table of Content
- How to Simplify a Square Root
- Introduction to Simplifying Square Roots
- Understanding the Basics
- Prime Factorization Method
- Using the Product Rule
- Using the Quotient Rule
- Simplifying Square Roots of Fractions
- Common Examples and Step-by-Step Solutions
- Simplifying Expressions Involving Multiple Radicals
- Special Cases: Surds and Perfect Squares
- Practice Problems and Solutions
- Advanced Techniques and Harder Examples
- Common Mistakes and How to Avoid Them
- Conclusion and Further Reading
- YOUTUBE:
How to Simplify a Square Root
Simplifying a square root involves expressing the square root in its simplest form. This often means reducing the number inside the radical to its smallest possible value by factoring out perfect squares. Here are the key steps to simplify square roots:
Steps to Simplify Square Roots
- Identify and factor the number inside the square root (radicand) into its prime factors.
- Look for pairs of prime factors, as they can be taken out of the square root.
- Rewrite the square root as the product of two square roots, one containing the perfect square and the other containing the remaining factors.
- Simplify by taking the square root of the perfect square and leaving the remaining factors inside the square root.
Examples
Example 1: Simplify √12
12 can be factored into 4 × 3. Therefore:
\[
\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3}
\]
Example 2: Simplify √45
45 can be factored into 9 × 5. Therefore:
\[
\sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5}
\]
Example 3: Simplify √18
18 can be factored into 9 × 2. Therefore:
\[
\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}
\]
Using the Product and Quotient Rules
The product rule states that the square root of a product is the product of the square roots:
\[
\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}
\]
Similarly, the quotient rule states that the square root of a quotient is the quotient of the square roots:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}, \quad b \neq 0
\]
Examples with Fractions
Example 4: Simplify \(\sqrt{\frac{36}{4}}\)
\[
\sqrt{\frac{36}{4}} = \frac{\sqrt{36}}{\sqrt{4}} = \frac{6}{2} = 3
\]
Example 5: Simplify \(\frac{\sqrt{30}}{\sqrt{10}}\)
\[
\frac{\sqrt{30}}{\sqrt{10}} = \sqrt{\frac{30}{10}} = \sqrt{3}
\]
Complex Examples
Example 6: Simplify \(2\sqrt{12} + 9\sqrt{3}\)
First, simplify \(2\sqrt{12}\):
\[
2\sqrt{12} = 2 \times 2\sqrt{3} = 4\sqrt{3}
\]
Then, add \(4\sqrt{3} + 9\sqrt{3}\):
\[
4\sqrt{3} + 9\sqrt{3} = (4 + 9)\sqrt{3} = 13\sqrt{3}
\]
Special Notes
A root that cannot be simplified further is called a surd. For example, \(\sqrt{3}\) is a surd, but \(\sqrt{4} = 2\) is not.

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots involves reducing the radicand (the number under the square root symbol) to its simplest form. This process is essential for solving many algebraic problems and can be done using various methods. Here, we'll explore the prime factorization method and the product rule to simplify square roots step-by-step.
Prime Factorization Method
To simplify a square root using the prime factorization method, follow these steps:
- Find the prime factors of the number under the square root.
- Pair the prime factors.
- Move each pair of prime factors out from under the square root.
- Multiply the numbers outside the square root and those remaining inside.
For example:
- Simplify \( \sqrt{72} \)
- Prime factors of 72: \( 2 \times 2 \times 2 \times 3 \times 3 \)
- Pair the prime factors: \( (2 \times 2) \) and \( (3 \times 3) \)
- Move pairs out: \( 2 \times 3 = 6 \)
- Remaining inside: \( 2 \)
- So, \( \sqrt{72} = 6\sqrt{2} \)
Using the Product Rule
The product rule for square roots states that \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \). This rule can be used to simplify square roots by breaking down the radicand into factors.
For example:
- Simplify \( \sqrt{50} \)
- Factor 50 into 25 and 2: \( \sqrt{50} = \sqrt{25 \times 2} \)
- Apply the product rule: \( \sqrt{25} \times \sqrt{2} \)
- Simplify: \( 5\sqrt{2} \)
Practice Examples
- Simplify \( \sqrt{18} \):
- Factor 18: \( 9 \times 2 \)
- Apply the product rule: \( \sqrt{9} \times \sqrt{2} = 3\sqrt{2} \)
- Simplify \( \sqrt{45} \):
- Factor 45: \( 9 \times 5 \)
- Apply the product rule: \( \sqrt{9} \times \sqrt{5} = 3\sqrt{5} \)
By mastering these methods, you can simplify any square root, making complex algebraic expressions much easier to handle.
Understanding the Basics
Simplifying square roots involves expressing a square root in its simplest form. To achieve this, you need to understand some fundamental concepts and rules. Here are the key points to get you started:
The Square Root Symbol
The square root symbol (√) represents the principal square root of a number. For a given non-negative number \( x \), the square root of \( x \) is a number \( y \) such that \( y^2 = x \). The expression under the square root symbol is called the radicand.
Basic Rule: The Product Rule
The product rule for square roots states that the square root of a product is the product of the square roots:
\[
\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}
\]
Steps to Simplify Square Roots
- Factor the Radicand: Begin by factoring the number inside the square root into its prime factors. For example, to simplify \( \sqrt{72} \), first factor 72 into 2, 2, 2, 3, and 3.
- Pair the Factors: Group the prime factors into pairs. Each pair of identical factors can be taken out of the square root as a single number. For \( \sqrt{72} \), the pairs are \( (2, 2) \) and \( (3, 3) \), with 2 and 3 left inside the root.
- Simplify: Multiply the numbers outside the square root and the remaining numbers inside the square root. For \( \sqrt{72} \): \[ \sqrt{72} = \sqrt{2 \times 2 \times 2 \times 3 \times 3} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \]
Examples
Let's look at a few examples to illustrate the process:
- Example 1: Simplify \( \sqrt{50} \) \[ \sqrt{50} = \sqrt{2 \times 5 \times 5} = 5\sqrt{2} \]
- Example 2: Simplify \( \sqrt{45} \) \[ \sqrt{45} = \sqrt{3 \times 3 \times 5} = 3\sqrt{5} \]
- Example 3: Simplify \( \sqrt{200} \) \[ \sqrt{200} = \sqrt{2 \times 2 \times 2 \times 5 \times 5} = 2 \times 5 \times \sqrt{2} = 10\sqrt{2} \]
By understanding and applying these basic rules and steps, you can simplify any square root to its simplest form, making calculations easier and more manageable.
Prime Factorization Method
The prime factorization method is a straightforward technique for simplifying square roots. This method involves breaking down the number inside the square root into its prime factors and then simplifying. Here is a step-by-step guide:
- Prime Factorization: Start by finding the prime factors of the number.
- Group the Pairs: Group the prime factors into pairs.
- Take One Factor from Each Pair: For each pair, take one factor out of the square root.
- Multiply the Factors Outside: Multiply the factors that have been taken out of the square root.
- Simplify the Remaining Factor: Multiply any remaining factors inside the square root.
Let’s go through a few examples to illustrate this method:
Example 1: Simplify √72
- Prime Factorization: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
- Group the Pairs: \( (2 \times 2) \) and \( (3 \times 3) \)
- Take One Factor from Each Pair: \( 2 \) and \( 3 \)
- Multiply the Factors Outside: \( 2 \times 3 = 6 \)
- Simplify the Remaining Factor: No remaining factors
- Result: \( \sqrt{72} = 6\sqrt{2} \)
Example 2: Simplify √180
- Prime Factorization: \( 180 = 2 \times 2 \times 3 \times 3 \times 5 \)
- Group the Pairs: \( (2 \times 2) \) and \( (3 \times 3) \)
- Take One Factor from Each Pair: \( 2 \) and \( 3 \)
- Multiply the Factors Outside: \( 2 \times 3 = 6 \)
- Simplify the Remaining Factor: \( \sqrt{5} \)
- Result: \( \sqrt{180} = 6\sqrt{5} \)
Example 3: Simplify √50
- Prime Factorization: \( 50 = 2 \times 5 \times 5 \)
- Group the Pairs: \( (5 \times 5) \)
- Take One Factor from Each Pair: \( 5 \)
- Multiply the Factors Outside: \( 5 \)
- Simplify the Remaining Factor: \( \sqrt{2} \)
- Result: \( \sqrt{50} = 5\sqrt{2} \)
By using the prime factorization method, you can simplify square roots efficiently and accurately. This method is particularly useful when dealing with larger numbers or when you need to simplify multiple square roots quickly.
Using the Product Rule
The product rule for square roots states that the square root of a product is equal to the product of the square roots of the factors. This rule can be applied to simplify complex square root expressions.
The general formula is:
To simplify a square root using the product rule, follow these steps:
- Factor any perfect squares out of the radicand (the number under the square root).
- Rewrite the radicand as a product of these factors.
- Apply the product rule to separate the factors into individual square roots.
- Simplify each square root, if possible.
Let's look at some examples:
Example 1
Simplify .
- Factor 300 into 100 and 3:
- Rewrite the square root:
- Simplify:
Example 2
Simplify .
- Factor 162 into 81 and 2:
- Rewrite the square root:
- Simplify:
Using the product rule makes simplifying square roots straightforward and helps in breaking down complex radical expressions into simpler parts.
Using the Quotient Rule
The quotient rule is a useful property when simplifying the square root of a fraction. This rule states that the square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator.
Mathematically, this is expressed as:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]
Here’s a step-by-step guide to simplify square roots using the quotient rule:
- Simplify the Fraction: First, simplify the fraction under the radical, if possible.
- Apply the Quotient Rule: Use the quotient rule to rewrite the radical expression as the quotient of two separate radicals.
- Simplify Each Radical: Simplify the radicals in the numerator and the denominator separately.
Let's look at some examples to understand this better:
Example 1: Simplify \(\sqrt{\frac{9}{16}}\)
- Simplify the fraction: \(\frac{9}{16}\) is already in simplest form.
- Apply the quotient rule: \[ \sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} \]
- Simplify each radical: \[ \frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4} \]
So, \(\sqrt{\frac{9}{16}} = \frac{3}{4}\).
Example 2: Simplify \(\sqrt{\frac{20}{25}}\)
- Simplify the fraction: \[ \frac{20}{25} = \frac{4}{5} \]
- Apply the quotient rule: \[ \sqrt{\frac{4}{5}} = \frac{\sqrt{4}}{\sqrt{5}} \]
- Simplify each radical:
\[
\frac{\sqrt{4}}{\sqrt{5}} = \frac{2}{\sqrt{5}}
\]
For simplicity, you might rationalize the denominator:
\[
\frac{2}{\sqrt{5}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{2\sqrt{5}}{5}
\]
Example 3: Simplify \(\sqrt{\frac{45x^5}{y^4}}\)
- Simplify the fraction: \(\frac{45x^5}{y^4}\) is already in simplest form.
- Apply the quotient rule: \[ \sqrt{\frac{45x^5}{y^4}} = \frac{\sqrt{45x^5}}{\sqrt{y^4}} \]
- Simplify each radical: \[ \frac{\sqrt{45x^5}}{\sqrt{y^4}} = \frac{\sqrt{9 \cdot 5 \cdot x^4 \cdot x}}{y^2} = \frac{3x^2\sqrt{5x}}{y^2} \]
By following these steps, you can simplify square roots of fractions effectively using the quotient rule.
Simplifying Square Roots of Fractions
Simplifying the square root of a fraction involves applying the square root to both the numerator and the denominator separately. Here are the detailed steps to achieve this:
-
Identify the fraction:
Consider the fraction inside the square root. For example, \(\sqrt{\frac{a}{b}}\).
-
Separate the square roots:
Use the property of square roots to separate the fraction into the square root of the numerator and the square root of the denominator:
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]
-
Simplify the numerator and the denominator:
Simplify \(\sqrt{a}\) and \(\sqrt{b}\) as much as possible. If either contains perfect squares, simplify them:
For example, \(\sqrt{18}\) can be simplified to \(3\sqrt{2}\) because \(18 = 9 \times 2\) and \(\sqrt{9} = 3\).
-
Rationalize the denominator (if necessary):
If the denominator is not a perfect square, rationalize it by multiplying both the numerator and the denominator by the square root of the denominator:
For example, to simplify \(\frac{\sqrt{2}}{\sqrt{5}}\), multiply by \(\frac{\sqrt{5}}{\sqrt{5}}\):
\[\frac{\sqrt{2}}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{10}}{5}\]
Here are some examples to illustrate the process:
-
Example 1: Simplify \(\sqrt{\frac{49}{64}}\)
Separate the square roots: \(\frac{\sqrt{49}}{\sqrt{64}} = \frac{7}{8}\)
-
Example 2: Simplify \(\sqrt{\frac{18}{50}}\)
Reduce the fraction first: \(\frac{18}{50} = \frac{9}{25}\)
Separate the square roots: \(\frac{\sqrt{9}}{\sqrt{25}} = \frac{3}{5}\)
-
Example 3: Simplify \(\sqrt{\frac{30}{32}}\)
Separate the square roots: \(\frac{\sqrt{30}}{\sqrt{32}}\)
Rationalize the denominator: \(\frac{\sqrt{30}}{\sqrt{32}} \times \frac{\sqrt{32}}{\sqrt{32}} = \frac{\sqrt{960}}{32}\)
Simplify further: \(\frac{8\sqrt{15}}{32} = \frac{\sqrt{15}}{4}\)
Common Examples and Step-by-Step Solutions
In this section, we will go through common examples of simplifying square roots with detailed, step-by-step solutions to help you understand the process.
Example 1: Simplify \(\sqrt{72}\)
- Prime factorize 72:
\(72 = 2 \times 2 \times 2 \times 3 \times 3\)
- Group the factors into pairs:
\(72 = (2 \times 2) \times (3 \times 3) \times 2\)
- Take one factor from each pair out of the square root:
\(\sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\)
Example 2: Simplify \(\sqrt{288}\)
- Prime factorize 288:
\(288 = 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3\)
- Group the factors into pairs:
\(288 = (2 \times 2) \times (2 \times 2) \times (3 \times 3) \times 2\)
- Take one factor from each pair out of the square root:
\(\sqrt{288} = \sqrt{(2 \times 2) \times (2 \times 2) \times (3 \times 3) \times 2} = 2 \times 2 \times 3 \times \sqrt{2} = 12\sqrt{2}\)
Example 3: Simplify \(\sqrt{108}\)
- Prime factorize 108:
\(108 = 2 \times 2 \times 3 \times 3 \times 3\)
- Group the factors into pairs:
\(108 = (2 \times 2) \times (3 \times 3) \times 3\)
- Take one factor from each pair out of the square root:
\(\sqrt{108} = \sqrt{(2 \times 2) \times (3 \times 3) \times 3} = 2 \times 3 \times \sqrt{3} = 6\sqrt{3}\)
Example 4: Simplify \(\sqrt{50}\)
- Prime factorize 50:
\(50 = 2 \times 5 \times 5\)
- Group the factors into pairs:
\(50 = 2 \times (5 \times 5)\)
- Take one factor from each pair out of the square root:
\(\sqrt{50} = \sqrt{2 \times (5 \times 5)} = 5 \sqrt{2}\)
Example 5: Simplify \(\sqrt{200}\)
- Prime factorize 200:
\(200 = 2 \times 2 \times 2 \times 5 \times 5\)
- Group the factors into pairs:
\(200 = (2 \times 2) \times (5 \times 5) \times 2\)
- Take one factor from each pair out of the square root:
\(\sqrt{200} = \sqrt{(2 \times 2) \times (5 \times 5) \times 2} = 2 \times 5 \times \sqrt{2} = 10 \sqrt{2}\)
Example 6: Simplify \(\sqrt{98}\)
- Prime factorize 98:
\(98 = 2 \times 7 \times 7\)
- Group the factors into pairs:
\(98 = 2 \times (7 \times 7)\)
- Take one factor from each pair out of the square root:
\(\sqrt{98} = \sqrt{2 \times (7 \times 7)} = 7 \sqrt{2}\)
Simplifying Expressions Involving Multiple Radicals
Simplifying expressions with multiple radicals can seem challenging, but with the right approach, it becomes much more manageable. Here are the steps you can follow:
Step-by-Step Process
- Identify and Separate the Radicals
- For example, given an expression like \( \sqrt{a} \cdot \sqrt{b} \), identify the individual radicals.
- Use the Product Rule
- The product rule states: \( \sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b} \).
- Apply this rule to combine the radicals under a single square root if possible.
- Simplify the Radicand
- Factor the radicand (the number inside the square root) into its prime factors.
- For example, \( \sqrt{50} = \sqrt{2 \cdot 5 \cdot 5} \).
- Extract the Square Factors
- Any factor that appears twice can be taken out of the square root as a single factor.
- For instance, \( \sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2} \).
- Combine Like Terms
- If you have similar radicals, combine them just like you would with like terms in algebra.
- Example: \( 3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2} \).
Examples
Let's look at some examples to illustrate these steps:
Example 1: \( \sqrt{18} \cdot \sqrt{2} \)
- Identify and Separate the Radicals:
- Given: \( \sqrt{18} \cdot \sqrt{2} \)
- Use the Product Rule:
- Combine: \( \sqrt{18 \cdot 2} = \sqrt{36} \)
- Simplify the Radicand:
- Since \( 36 = 6 \cdot 6 \), we get \( \sqrt{36} = 6 \)
- Result: \( 6 \)
Example 2: \( \sqrt{12} + 2\sqrt{3} \)
- Identify and Separate the Radicals:
- Given: \( \sqrt{12} + 2\sqrt{3} \)
- Use the Product Rule:
- Simplify \( \sqrt{12} \) by factoring into \( \sqrt{4 \cdot 3} = 2\sqrt{3} \)
- Combine Like Terms:
- \( 2\sqrt{3} + 2\sqrt{3} = 4\sqrt{3} \)
- Result: \( 4\sqrt{3} \)
Example 3: \( \sqrt{8} \cdot \sqrt{2} \)
- Identify and Separate the Radicals:
- Given: \( \sqrt{8} \cdot \sqrt{2} \)
- Use the Product Rule:
- Combine: \( \sqrt{8 \cdot 2} = \sqrt{16} \)
- Simplify the Radicand:
- \( \sqrt{16} = 4 \)
- Result: \( 4 \)
Conclusion
Simplifying expressions involving multiple radicals is all about using the product rule, simplifying the radicand, and combining like terms. With practice, these steps will become second nature.

Special Cases: Surds and Perfect Squares
When simplifying square roots, there are special cases involving surds and perfect squares. Understanding these cases can help simplify the process and make calculations easier.
Surds
A surd is an irrational number that can't be simplified to remove the square root. For example, \(\sqrt{2}\), \(\sqrt{3}\), and \(\sqrt{5}\) are surds because they cannot be simplified to a rational number.
To simplify a surd:
- Find a square number that is a factor of the number inside the root sign. For example, in \(\sqrt{72}\), 72 = 36 × 2, where 36 is a square number.
- Rewrite the surd using the product rule: \(\sqrt{72} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\).
- If there are more square factors, continue simplifying. For instance, \(\sqrt{48} = \sqrt{16} \times \sqrt{3} = 4\sqrt{3}\).
Here are some examples:
- \(\sqrt{50} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\)
- \(\sqrt{28} = \sqrt{4} \times \sqrt{7} = 2\sqrt{7}\)
- \(\sqrt{63} = \sqrt{9} \times \sqrt{7} = 3\sqrt{7}\)
Perfect Squares
A perfect square is a number that can be expressed as the square of an integer. For example, 1, 4, 9, 16, and 25 are perfect squares. When simplifying the square root of a perfect square, the result is always an integer.
For example:
- \(\sqrt{16} = 4\)
- \(\sqrt{25} = 5\)
- \(\sqrt{36} = 6\)
When dealing with expressions involving perfect squares and surds, use the following steps:
- Identify and separate the perfect squares and surds.
- Apply the product rule to simplify the square roots of the perfect squares.
- Combine the results for a simplified expression.
For example:
Simplify \(\sqrt{72} \times \sqrt{18}\)
- \(\sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2}\)
- \(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
- \(6\sqrt{2} \times 3\sqrt{2} = 18 \times 2 = 36\)
The simplified result is 36.
Understanding these special cases and the rules for simplifying surds and perfect squares will make working with square roots more manageable and less error-prone.
Practice Problems and Solutions
Here are some practice problems to help you master simplifying square roots. Follow the detailed solutions step-by-step.
Problem 1: Simplify √72
- Factor 72 into its prime factors: 72 = 2 × 2 × 2 × 3 × 3.
- Group the prime factors into pairs: (2 × 2) × (3 × 3) × 2.
- Take one factor from each pair out of the square root: √(2² × 3² × 2) = 2 × 3 √2.
- Multiply the factors: 2 × 3 = 6. Therefore, √72 = 6√2.
Problem 2: Simplify √288
- Factor 288 into its prime factors: 288 = 2 × 2 × 2 × 2 × 2 × 3 × 3.
- Group the prime factors into pairs: (2 × 2) × (2 × 2) × (3 × 3) × 2.
- Take one factor from each pair out of the square root: √(2⁴ × 3² × 2) = 2² × 3 √2.
- Multiply the factors: 2² = 4, and 4 × 3 = 12. Therefore, √288 = 12√2.
Problem 3: Simplify √108
- Factor 108 into its prime factors: 108 = 2 × 2 × 3 × 3 × 3.
- Group the prime factors into pairs: (2 × 2) × (3 × 3) × 3.
- Take one factor from each pair out of the square root: √(2² × 3² × 3) = 2 × 3 √3.
- Multiply the factors: 2 × 3 = 6. Therefore, √108 = 6√3.
Problem 4: Simplify √60
- Factor 60 into its prime factors: 60 = 2 × 2 × 3 × 5.
- Group the prime factors into pairs: (2 × 2) × 3 × 5.
- Take one factor from each pair out of the square root: √(2² × 3 × 5) = 2 √(3 × 5).
- Multiply the remaining factors inside the square root: √(3 × 5) = √15. Therefore, √60 = 2√15.
Problem 5: Simplify √18
- Factor 18 into its prime factors: 18 = 2 × 3 × 3.
- Group the prime factors into pairs: 2 × (3 × 3).
- Take one factor from each pair out of the square root: √(2 × 3²) = 3 √2.
- Therefore, √18 = 3√2.
Problem 6: Simplify √45
- Factor 45 into its prime factors: 45 = 3 × 3 × 5.
- Group the prime factors into pairs: (3 × 3) × 5.
- Take one factor from each pair out of the square root: √(3² × 5) = 3 √5.
- Therefore, √45 = 3√5.
Problem 7: Simplify √8
- Factor 8 into its prime factors: 8 = 2 × 2 × 2.
- Group the prime factors into pairs: (2 × 2) × 2.
- Take one factor from each pair out of the square root: √(2² × 2) = 2 √2.
- Therefore, √8 = 2√2.
Keep practicing these problems to improve your skills in simplifying square roots. Remember to factor numbers into their prime factors and group them to simplify effectively.
Advanced Techniques and Harder Examples
When dealing with more complex square root simplifications, advanced techniques such as rationalizing the denominator, denesting radicals, and solving radical equations come into play. Here are detailed steps and examples for each method:
1. Rationalizing the Denominator
To rationalize the denominator, multiply the numerator and the denominator by a suitable value to eliminate the radical in the denominator.
- Example: Simplify \( \frac{5}{\sqrt{2}} \)
- Multiply numerator and denominator by \( \sqrt{2} \):
- \( \frac{5 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} = \frac{5\sqrt{2}}{2} \)
2. Denesting Radicals
Denesting involves expressing nested radicals in a simpler form. This often requires algebraic manipulation and understanding of identities.
- Example: Simplify \( \sqrt{2 + \sqrt{3}} \)
- Assume \( \sqrt{2 + \sqrt{3}} = \sqrt{a} + \sqrt{b} \)
- Square both sides: \( 2 + \sqrt{3} = a + b + 2\sqrt{ab} \)
- Equate rational and irrational parts: \( a + b = 2 \) and \( 2\sqrt{ab} = \sqrt{3} \)
- Solve the system: \( ab = \frac{3}{4} \)
- Possible values: \( a = \frac{3}{2} \), \( b = \frac{1}{2} \) (or vice versa)
- Thus, \( \sqrt{2 + \sqrt{3}} = \sqrt{\frac{3}{2}} + \sqrt{\frac{1}{2}} \)
3. Solving Radical Equations
Radical equations often require isolating the radical and squaring both sides of the equation. This may need to be repeated until the radical is eliminated.
- Example: Solve \( \sqrt{x-3} + \sqrt{x} = 3 \)
- Isolate one radical: \( \sqrt{x-3} = 3 - \sqrt{x} \)
- Square both sides: \( x - 3 = 9 - 6\sqrt{x} + x \)
- Simplify and isolate the remaining radical: \( -3 = 9 - 6\sqrt{x} \)
- Solve for \( \sqrt{x} \): \( 6\sqrt{x} = 12 \Rightarrow \sqrt{x} = 2 \Rightarrow x = 4 \)
- Check the solution in the original equation to confirm.
These methods require careful algebraic manipulation and verification to ensure that the solutions are correct and simplified appropriately. Practice with various examples helps in mastering these advanced techniques.
Common Mistakes and How to Avoid Them
Simplifying square roots can sometimes be tricky, and it's easy to make mistakes. Here are some common errors and tips on how to avoid them:
- Forgetting to check for perfect squares: Before simplifying, always check if the number is a perfect square. For example, √36 simplifies directly to 6.
- Rushing through the process: Simplification requires careful step-by-step calculations. Take your time to avoid errors.
- Incorrectly handling negative square roots: Remember that √(-1) is not a real number. For real numbers, square roots should be non-negative.
- Not fully simplifying: Ensure all factors are simplified. For instance, √72 should be simplified to 6√2, not left as √72.
Here are some detailed examples to illustrate these points:
| Example | Common Mistake | Correct Approach |
|---|---|---|
| √50 | Leaving as √50 | Recognize that 50 = 25 * 2, so √50 = √(25 * 2) = √25 * √2 = 5√2 |
| √18 | Leaving as √18 | Recognize that 18 = 9 * 2, so √18 = √(9 * 2) = √9 * √2 = 3√2 |
| √(-16) | Treating √(-16) as a real number | Understand that √(-16) is 4i in the complex number system |
By being aware of these common pitfalls and taking a methodical approach, you can simplify square roots accurately and efficiently. Practice regularly, and don't hesitate to seek help from teachers or online resources if needed.

Conclusion and Further Reading
Simplifying square roots is a fundamental skill in mathematics that can make complex calculations easier and more elegant. By mastering this technique, you can solve problems more efficiently and gain a deeper understanding of higher-level mathematical concepts.
As you continue your mathematical journey, remember these key points:
- Always look for perfect squares within the radicand to simplify the square root.
- Use prime factorization to break down the number inside the square root for easier simplification.
- Apply the product and quotient rules for square roots to handle more complex expressions.
To further enhance your skills, consider exploring additional resources and practice problems. Here are some recommendations for further reading:
- - A comprehensive guide with videos and practice exercises.
- - An easy-to-follow explanation with examples and visual aids.
- - Step-by-step instructions with tips and common pitfalls to avoid.
Embrace the challenges of simplifying square roots, practice regularly, and don't hesitate to seek help from tutors or online forums when needed. Remember, math is not just about numbers; it's a journey of discovery and learning.
Thank you for exploring the art of simplifying square roots with us. Keep practicing, stay curious, and enjoy the mathematical adventures ahead!
Cách Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Cách Đơn Giản Hóa Căn Bậc Hai