Topic how do you simplify square roots: Simplifying square roots can seem challenging, but with the right approach, it becomes straightforward. This guide will walk you through the process, explaining methods like prime factorization and the quotient property, making it easy for you to master this essential math skill.
Table of Content
- Simplifying Square Roots
- Introduction to Simplifying Square Roots
- Understanding Square Roots
- Basic Rules for Simplifying Square Roots
- Prime Factorization Method
- Simplifying Square Roots of Perfect Squares
- Simplifying Non-Perfect Squares
- Combining Square Roots
- Simplifying Square Roots with Fractions
- Quotient Property of Square Roots
- Simplifying Square Roots of Variables
- Common Mistakes to Avoid
- Practice Problems
- Advanced Examples
- Using Technology to Simplify Square Roots
- YOUTUBE: Học cách đơn giản hóa căn bậc hai trong video này từ Khan Academy, bao gồm các khái niệm về số mũ, căn bậc hai và ký hiệu khoa học.
Simplifying Square Roots
Simplifying square roots involves expressing the square root in its simplest form. Here are the steps and examples to help you understand the process:
Steps to Simplify Square Roots
- Factor out the perfect squares from the number inside the square root.
- Separate the perfect squares using the property of square roots: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \).
- Simplify the square roots of the perfect squares.
Examples
Example 1: Simplify \( \sqrt{72} \)
- Factor 72 into prime factors: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
- Group the pairs of factors: \( 72 = (2 \times 2) \times (3 \times 3) \times 2 = 4 \times 9 \times 2 \).
- Simplify: \( \sqrt{72} = \sqrt{4 \times 9 \times 2} = \sqrt{4} \cdot \sqrt{9} \cdot \sqrt{2} = 2 \cdot 3 \cdot \sqrt{2} = 6\sqrt{2} \).
Example 2: Simplify \( \sqrt{45} \)
- Factor 45 into prime factors: \( 45 = 3 \times 3 \times 5 \).
- Group the pairs of factors: \( 45 = (3 \times 3) \times 5 = 9 \times 5 \).
- Simplify: \( \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \cdot \sqrt{5} = 3\sqrt{5} \).
Simplifying Square Roots of Fractions
To simplify square roots of fractions, use the quotient property of square roots:
\[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
Example: Simplify \( \sqrt{\frac{72z^{12}}{2z^{10}}} \)
- Simplify the fraction inside the square root: \( \frac{72z^{12}}{2z^{10}} = 36z^2 \).
- Apply the square root: \( \sqrt{36z^2} = 6z \).
Using Prime Factorization
Another method to simplify square roots is to use prime factorization:
- Break the number into its prime factors.
- For each pair of factors, take one factor out of the square root.
- Multiply the factors outside the square root together.
Example: Simplify \( \sqrt{90} \)
- Factor 90 into prime factors: \( 90 = 2 \times 3 \times 3 \times 5 \).
- Group the pairs of factors: \( 90 = (3 \times 3) \times 2 \times 5 \).
- Simplify: \( \sqrt{90} = \sqrt{9 \times 10} = \sqrt{9} \cdot \sqrt{10} = 3\sqrt{10} \).
Conclusion
By following these methods, you can simplify square roots efficiently. Whether using prime factorization or the properties of square roots, the key is to factorize the number and simplify step by step.

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots is an essential skill in algebra that involves expressing a square root in its simplest form. The process typically involves breaking down the number inside the square root (the radicand) into its prime factors and simplifying where possible.
To start, recognize that a square root can be simplified by finding perfect square factors of the radicand. For instance, the square root of 12 can be simplified because 12 can be factored into 4 and 3, where 4 is a perfect square.
- Identify and factor the radicand into its prime factors.
- Group the prime factors into pairs of identical factors.
- Move one factor of each pair outside the square root symbol.
- Multiply the factors outside the square root and simplify the expression.
For example, to simplify \( \sqrt{12} \):
- Factor 12 into 4 and 3: \( \sqrt{12} = \sqrt{4 \times 3} \)
- Since 4 is a perfect square, simplify: \( \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} \)
- Simplify \( \sqrt{4} \) to 2: \( 2\sqrt{3} \)
Thus, \( \sqrt{12} \) simplifies to \( 2\sqrt{3} \).
This method can be applied to any square root to simplify it, making it easier to work with in further calculations.
Understanding Square Roots
Square roots are mathematical operations that determine what number, when multiplied by itself, equals the given number. They are represented using the radical symbol \( \sqrt{} \). For example, \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \). Understanding square roots is fundamental to simplifying them and performing other mathematical operations involving radicals.
Here are key points to understanding square roots:
- The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). This is written as \( \sqrt{x} \).
- Square roots of perfect squares (numbers like 1, 4, 9, 16, etc.) are integers. For example, \( \sqrt{16} = 4 \) and \( \sqrt{81} = 9 \).
- Non-perfect squares have irrational square roots. For example, \( \sqrt{2} \approx 1.414 \) and \( \sqrt{3} \approx 1.732 \).
- Square roots can be simplified by factoring the number inside the radical to find perfect square factors.
- The properties of square roots are crucial for simplification and include:
- \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \)
- \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) where \( b \neq 0 \)
Understanding these basics will help you simplify square roots and work more effectively with radical expressions.
Basic Rules for Simplifying Square Roots
To simplify square roots, we use several fundamental rules and properties. Understanding and applying these rules helps in breaking down complex square root expressions into simpler forms.
Here are the basic rules for simplifying square roots:
- Prime Factorization: Break the number inside the square root into its prime factors. For each pair of identical factors, one can be taken out of the square root.
- Product Rule: The square root of a product is the product of the square roots of the factors. This can be expressed as \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\).
- Quotient Rule: The square root of a quotient is the quotient of the square roots of the numerator and denominator. This can be expressed as \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
- Perfect Squares: Recognize perfect squares within the radicand (the number inside the square root). A perfect square is a number that has an integer as its square root (e.g., 1, 4, 9, 16).
Here is a step-by-step process to simplify a square root using these rules:
- Identify and factorize the radicand into its prime factors. For example, \(\sqrt{72} = \sqrt{2 \times 2 \times 2 \times 3 \times 3}\).
- Group the prime factors into pairs. For each pair, take one factor out of the square root. In our example, \(\sqrt{2 \times 2 \times 2 \times 3 \times 3} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\).
- If dealing with a fraction, use the quotient rule to separate the numerator and denominator. Simplify each part separately and then divide the results. For instance, \(\sqrt{\frac{8}{50}} = \frac{\sqrt{8}}{\sqrt{50}} = \frac{2\sqrt{2}}{5\sqrt{2}} = \frac{2}{5}\).
- Combine all simplified parts. Ensure there are no perfect squares left inside the square root.
By following these steps and rules, you can simplify most square root expressions efficiently and accurately.
Prime Factorization Method
The prime factorization method is a reliable way to simplify square roots by breaking down a number into its prime factors. Here are the detailed steps to simplify a square root using this method:
- Factor the number into prime factors: Start by expressing the number inside the square root as a product of prime numbers. For example, to simplify \(\sqrt{72}\), you first express 72 as \(2 \times 2 \times 2 \times 3 \times 3\).
- Pair the prime factors: Next, group the prime factors into pairs. Each pair of identical prime factors can be taken out of the square root. For \(\sqrt{72}\), you group the factors as \((2 \times 2) \times (3 \times 3) \times 2\).
- Take one factor out of each pair: For each pair of prime factors, take one factor out of the square root. Using the example, this gives \(2 \times 3 \times \sqrt{2}\).
- Multiply the factors outside the square root: Finally, multiply the factors taken out of the square root. For \(\sqrt{72}\), this results in \(6\sqrt{2}\).
This method can be applied to any number to simplify its square root effectively. For instance, \(\sqrt{180}\) is simplified as follows:
- Prime factorization: \(180 = 2 \times 2 \times 3 \times 3 \times 5\).
- Pair the factors: \((2 \times 2) \times (3 \times 3) \times 5\).
- Take out one factor from each pair: \(2 \times 3 \times \sqrt{5} = 6\sqrt{5}\).
By following these steps, you can simplify any square root by using the prime factorization method.
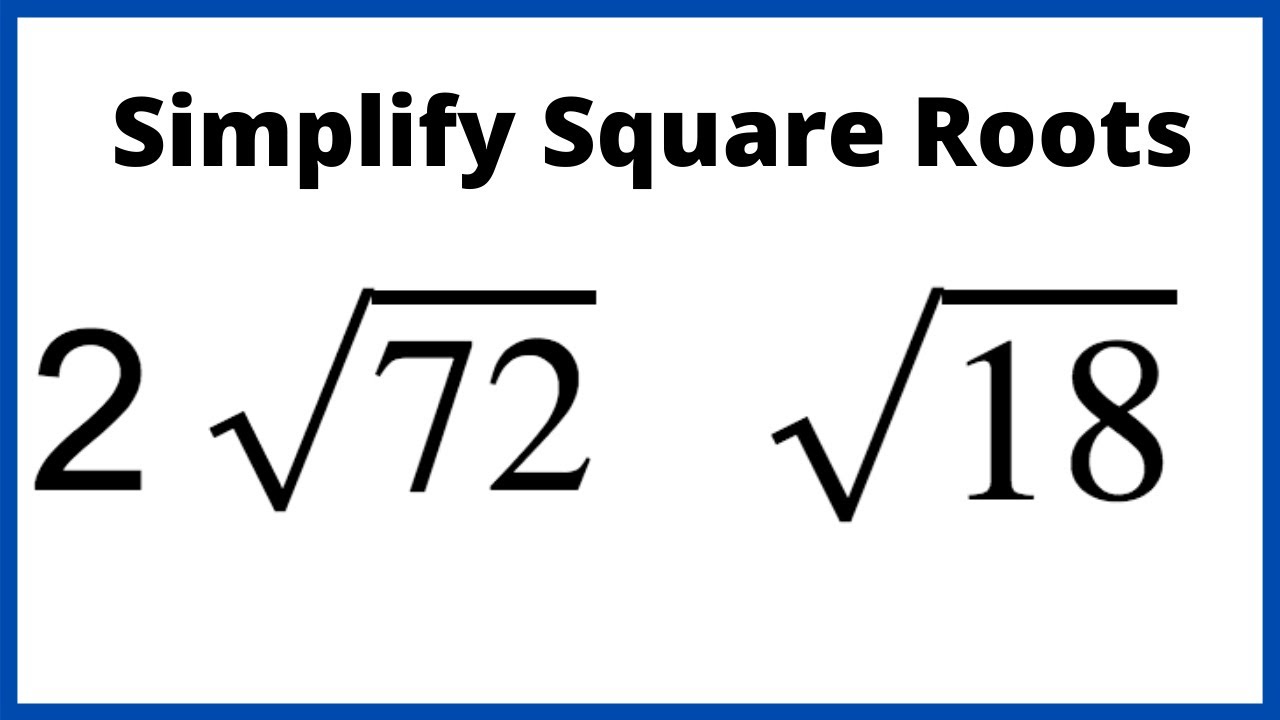
Simplifying Square Roots of Perfect Squares
When simplifying square roots of perfect squares, the process is straightforward because perfect squares have whole numbers as their square roots. Here is a step-by-step guide to help you simplify these square roots:
- Identify the Perfect Square: A perfect square is a number that is the square of an integer. For example, \(1, 4, 9, 16, 25,\) etc.
- Find the Square Root: Determine the integer whose square gives the original number. This integer is the simplified form of the square root.
- Examples:
- \(\sqrt{16}\): Since \(16\) is \(4^2\), the square root of \(16\) is \(4\). Therefore, \(\sqrt{16} = 4\).
- \(\sqrt{25}\): Since \(25\) is \(5^2\), the square root of \(25\) is \(5\). Therefore, \(\sqrt{25} = 5\).
- \(\sqrt{36}\): Since \(36\) is \(6^2\), the square root of \(36\) is \(6\). Therefore, \(\sqrt{36} = 6\).
These steps illustrate that simplifying the square root of a perfect square is simply recognizing the number as a product of an integer multiplied by itself and then taking that integer as the result.
Simplifying Non-Perfect Squares
When dealing with square roots of non-perfect squares, the goal is to simplify the expression to its simplest form. This involves breaking down the number under the square root into its prime factors and then simplifying by grouping pairs of prime factors.
Here is a step-by-step process to simplify square roots of non-perfect squares:
- Find the prime factorization: Break down the number under the square root into its prime factors. For example, for \( \sqrt{18} \), the prime factorization of 18 is \( 2 \times 3 \times 3 \).
- Group the pairs: Identify and group the pairs of prime factors. In the case of \( \sqrt{18} \), we have one pair of 3s.
- Simplify by taking out the pairs: For each pair of factors, take one factor out of the square root. This means \( \sqrt{18} = \sqrt{3 \times 3 \times 2} = 3\sqrt{2} \).
Let's look at another example:
Example: Simplify \( \sqrt{50} \).
- Find the prime factorization: \( 50 = 2 \times 5 \times 5 \).
- Group the pairs: The pairs are \( 5 \times 5 \).
- Simplify by taking out the pairs: \( \sqrt{50} = \sqrt{5 \times 5 \times 2} = 5\sqrt{2} \).
Another example to reinforce the concept:
Example: Simplify \( \sqrt{72} \).
- Find the prime factorization: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
- Group the pairs: We have pairs \( 2 \times 2 \) and \( 3 \times 3 \).
- Simplify by taking out the pairs: \( \sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \sqrt{2} = 6\sqrt{2} \).
This method ensures that the square root is expressed in its simplest form. For larger numbers, this process can be repeated, and using a calculator to find the prime factors can be helpful. Remember, the goal is to simplify the expression as much as possible while keeping it accurate.
Combining Square Roots
Combining square roots can often simplify expressions and make calculations easier. Here are some steps and examples to guide you through this process.
1. Combining Square Roots with Multiplication
When you multiply two square roots, you can combine them under a single radical.
- Example: Combine \( \sqrt{6} \) and \( \sqrt{15} \).
- Step 1: Multiply the numbers inside the radicals: \( \sqrt{6} \times \sqrt{15} = \sqrt{6 \times 15} \).
- Step 2: Simplify inside the radical: \( \sqrt{6 \times 15} = \sqrt{90} \).
- Step 3: Factorize the number under the radical: \( \sqrt{90} = \sqrt{9 \times 10} \).
- Step 4: Simplify the square root of any perfect squares: \( \sqrt{9 \times 10} = 3\sqrt{10} \).
- Result: \( \sqrt{6} \times \sqrt{15} = 3\sqrt{10} \).
2. Combining Square Roots with Addition and Subtraction
To combine square roots through addition or subtraction, they must have the same radicand (the number under the radical).
- Example: Combine \( 2\sqrt{3} \) and \( 5\sqrt{3} \).
- Step 1: Ensure the radicands are the same: \( 2\sqrt{3} \) and \( 5\sqrt{3} \) both have \( \sqrt{3} \).
- Step 2: Add the coefficients: \( 2 + 5 = 7 \).
- Result: \( 2\sqrt{3} + 5\sqrt{3} = 7\sqrt{3} \).
3. Examples of Combining Square Roots
- Example: Combine \( \sqrt{8} \) and \( \sqrt{2} \).
- Step 1: Simplify each square root if possible: \( \sqrt{8} = 2\sqrt{2} \).
- Step 2: Combine like terms: \( 2\sqrt{2} + \sqrt{2} = 3\sqrt{2} \).
- Result: \( \sqrt{8} + \sqrt{2} = 3\sqrt{2} \).
4. Combining Square Roots with Division
When dividing square roots, you can use the property of radicals to combine them.
- Example: Combine \( \frac{\sqrt{50}}{\sqrt{2}} \).
- Step 1: Combine the square roots under one radical: \( \frac{\sqrt{50}}{\sqrt{2}} = \sqrt{\frac{50}{2}} \).
- Step 2: Simplify inside the radical: \( \sqrt{\frac{50}{2}} = \sqrt{25} \).
- Step 3: Simplify the radical: \( \sqrt{25} = 5 \).
- Result: \( \frac{\sqrt{50}}{\sqrt{2}} = 5 \).
By following these steps and examples, you can effectively combine and simplify square roots in various mathematical expressions.
Simplifying Square Roots with Fractions
Simplifying square roots that contain fractions involves a few steps. By using the Quotient Property of Square Roots, we can break down and simplify these expressions more easily. Here’s a step-by-step guide:
Simplify the Fraction if Possible: If the fraction inside the square root can be simplified, do that first. This makes the subsequent steps easier.
Apply the Quotient Property of Square Roots: The property states that the square root of a fraction is equal to the square root of the numerator divided by the square root of the denominator:
$$\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$$
Ensure that both the numerator and the denominator are non-negative.
Simplify the Radicals: Simplify the square roots in both the numerator and the denominator. This step might involve finding perfect squares within the numbers or variables.
Rationalize the Denominator (if necessary): If the denominator is not a perfect square, multiply the numerator and the denominator by a number that will make the denominator a perfect square. This is called rationalizing the denominator.
Examples
Example 1: Simplify $$\sqrt{\frac{9}{16}}$$
Step 1: Both 9 and 16 are perfect squares.
Step 2: Apply the Quotient Property:
$$\sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4}$$
Example 2: Simplify $$\sqrt{\frac{18}{50}}$$
Step 1: Simplify the fraction: $$\frac{18}{50} = \frac{9}{25}$$
Step 2: Apply the Quotient Property:
$$\sqrt{\frac{9}{25}} = \frac{\sqrt{9}}{\sqrt{25}} = \frac{3}{5}$$
Example 3: Simplify $$\sqrt{\frac{5}{8}}$$
Step 1: Apply the Quotient Property directly:
$$\sqrt{\frac{5}{8}} = \frac{\sqrt{5}}{\sqrt{8}}$$
Step 2: Simplify the denominator:
$$\frac{\sqrt{5}}{\sqrt{8}} = \frac{\sqrt{5}}{2\sqrt{2}}$$
Step 3: Rationalize the denominator:
$$\frac{\sqrt{5}}{2\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{10}}{4}$$
These steps and examples show how to approach simplifying square roots that involve fractions, ensuring clarity and precision in your calculations.

Quotient Property of Square Roots
The Quotient Property of Square Roots is a useful tool for simplifying square roots that involve fractions. This property states that the square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. Mathematically, this can be expressed as:
\[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
Here are the steps to simplify square roots using the Quotient Property:
-
Simplify the fraction inside the square root, if possible: Before applying the quotient property, check if the fraction inside the square root can be simplified. For example, \( \frac{8}{32} \) simplifies to \( \frac{1}{4} \).
-
Apply the Quotient Property: Use the property to rewrite the square root of the fraction as the quotient of the square roots of the numerator and the denominator. For example, \(\sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}}\).
-
Simplify the square roots: Finally, simplify the square roots of the numerator and the denominator separately. For example, \(\frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2}\).
Let's look at a few examples:
-
Simplify \( \sqrt{\frac{25}{9}} \):
- Rewrite using the quotient property: \( \frac{\sqrt{25}}{\sqrt{9}} \)
- Simplify the square roots: \( \frac{5}{3} \)
So, \( \sqrt{\frac{25}{9}} = \frac{5}{3} \).
-
Simplify \( \sqrt{\frac{50}{2}} \):
- Simplify the fraction: \( \frac{50}{2} = 25 \)
- Apply the square root: \( \sqrt{25} = 5 \)
So, \( \sqrt{\frac{50}{2}} = 5 \).
-
Simplify \( \sqrt{\frac{18}{32}} \):
- Simplify the fraction: \( \frac{18}{32} = \frac{9}{16} \)
- Rewrite using the quotient property: \( \frac{\sqrt{9}}{\sqrt{16}} \)
- Simplify the square roots: \( \frac{3}{4} \)
So, \( \sqrt{\frac{18}{32}} = \frac{3}{4} \).
Using the Quotient Property of Square Roots can greatly simplify the process of working with square roots involving fractions. Practice applying these steps to become more comfortable with the process.
Simplifying Square Roots of Variables
When simplifying square roots that involve variables, follow these steps:
- Factor the expression inside the square root: Express the radicand as a product of its factors.
- Identify perfect square factors: Identify any factors that are perfect squares.
- Apply the square root property: Take the square root of each perfect square factor.
- Combine like terms: Combine the square roots of the perfect square factors and any remaining factors outside the square root symbol.
Let's consider an example:
Given the expression \( \sqrt{18x^2} \), we can simplify it as follows:
- Factor inside the square root: \( 18x^2 = 9 \cdot 2 \cdot x^2 \).
- Identify perfect squares: \( 9 \) is a perfect square.
- Apply the square root property: \( \sqrt{9 \cdot 2 \cdot x^2} = \sqrt{9} \cdot \sqrt{2} \cdot \sqrt{x^2} \).
- Combine like terms: \( \sqrt{9} \cdot \sqrt{2} \cdot \sqrt{x^2} = 3x\sqrt{2} \).
Therefore, \( \sqrt{18x^2} = 3x\sqrt{2} \).
Common Mistakes to Avoid
- Forgetting to simplify perfect squares: Always check if there are perfect square factors that can be simplified.
- Mixing up addition and multiplication under the square root: Remember that square roots do not distribute over addition, only over multiplication.
- Incorrectly applying square roots to variables: Ensure to apply the square root property correctly to each factor inside the square root, especially when dealing with variables.
- Ignoring the square root of negative numbers: Be mindful of the square root of negative numbers, which involve imaginary numbers and should be handled appropriately.
- Skipping steps in simplification: Take each step in simplification carefully to avoid missing factors or making calculation errors.
Practice Problems
Practice simplifying square roots with the following problems:
- Simplify \( \sqrt{50} \).
- Simplify \( \sqrt{75} \).
- Simplify \( \sqrt{18x^2} \).
- Simplify \( \sqrt{12y^3} \).
- Simplify \( \sqrt{2a^4b^2} \).

Advanced Examples
Explore these advanced examples of simplifying square roots:
- Simplify \( \sqrt{27} \).
- Simplify \( \sqrt{\frac{32}{9}} \).
- Simplify \( \sqrt{50x^3y^5} \).
- Simplify \( \sqrt{\frac{18a^2b}{3ab^2}} \).
- Simplify \( \sqrt{72z^4} \).
Using Technology to Simplify Square Roots
Technology can greatly assist in simplifying square roots, making the process quicker and more accurate. Here are some tools and methods you can use:
1. Graphing Calculators
Graphing calculators such as the TI-83 and TI-86 are powerful tools for simplifying square roots. Here’s how you can use them:
- Turn on the calculator and press the square root (√) button.
- Enter the number you wish to simplify.
- Press the "Enter" key to get the simplified square root.
These calculators can handle more complex expressions and even variables, making them a valuable resource for students and professionals alike.
2. Online Calculators and Apps
Several online calculators and mobile apps are available to simplify square roots. Websites like Symbolab and Khan Academy provide step-by-step solutions:
- Symbolab: Enter the square root expression, and it will show the simplified result along with the steps taken to simplify it.
- Khan Academy: Offers instructional videos and practice problems to help understand the process of simplifying square roots.
3. Spreadsheet Software
Spreadsheet programs like Microsoft Excel can also be used to simplify square roots:
- Open Excel and select a cell.
- Type the formula
=SQRT(number), replacing "number" with the value you wish to simplify. - Press "Enter" to display the simplified square root.
Excel can handle more complex calculations, including those involving variables and larger expressions.
4. Educational Websites
Websites such as Wisc-Online offer tutorials and interactive lessons on simplifying square roots. These resources can be very helpful for visual learners and those who prefer interactive content.
5. Mobile Apps
Apps like Photomath allow users to take pictures of their math problems and receive instant solutions, including the steps to simplify square roots. This is particularly useful for quick checks and learning on the go.
Using these technologies not only simplifies the process but also helps in understanding the underlying principles, making learning more effective and engaging.
Học cách đơn giản hóa căn bậc hai trong video này từ Khan Academy, bao gồm các khái niệm về số mũ, căn bậc hai và ký hiệu khoa học.
Đơn giản hóa căn bậc hai | Số mũ, căn bậc hai, và ký hiệu khoa học | Tiền Đại số | Khan Academy
READ MORE:
Học cách đơn giản hóa căn bậc hai một cách dễ dàng và hiệu quả trong video này.
Cách Đơn Giản Hóa Căn Bậc Hai










