Topic how do you solve the square root of a number: Discover the essential methods and techniques for solving the square root of a number in this comprehensive guide. Whether you're a student or just curious, learn how to tackle square roots with confidence using simple explanations and practical examples. Start mastering square roots today!
Table of Content
- How to Solve the Square Root of a Number
- Introduction to Square Roots
- Understanding Square Numbers
- Square Roots: Basic Concepts
- The Relationship Between Squares and Square Roots
- Perfect Squares and Their Roots
- Calculating Square Roots of Non-Perfect Squares
- Methods to Calculate Square Roots
- Prime Factorization Method
- Long Division Method
- Using a Calculator for Square Roots
- Handling Decimal Numbers
- Square Roots of Negative Numbers
- Visualizing Square Roots
- Practical Applications of Square Roots
- Fun Facts About Square Roots
- YOUTUBE: Khám phá khái niệm căn bậc hai với Thầy J trong video này. Tìm hiểu cách tính căn bậc hai và ứng dụng của nó trong toán học.
How to Solve the Square Root of a Number
The square root of a number is a value that, when multiplied by itself, gives the original number. To solve the square root of a number, follow these detailed steps:
1. Understanding Square Roots
Square roots are usually denoted by the symbol √. For example, √9 = 3 because 3 * 3 = 9.
2. Methods to Find Square Roots
- Using Prime Factorization
- Using the Long Division Method
- Using Estimation and Approximation
3. Prime Factorization Method
- Factorize the number into its prime factors.
- Pair the prime factors.
- Take one factor from each pair and multiply them.
Example: Find the square root of 36
- 36 = 2 * 2 * 3 * 3
- Pairing the factors: (2*2) and (3*3)
- Taking one factor from each pair: 2 and 3
- Multiplying them: 2 * 3 = 6
So, √36 = 6
4. Long Division Method
- Group the digits in pairs, starting from the decimal point.
- Find the largest number whose square is less than or equal to the first group.
- Subtract the square of the number found from the first group and bring down the next group of digits.
- Double the quotient obtained and use it as a new divisor.
- Find a digit to append to the new divisor, such that the product is less than or equal to the current dividend.
- Repeat the process until you have calculated to the desired precision.
5. Estimation and Approximation
- Find two perfect square numbers between which the given number lies.
- Estimate the square root as a decimal between the two square roots.
- Refine the estimate by averaging and adjusting as necessary.
Example: Estimate √50
- 72 = 49 and 82 = 64
- √50 is between 7 and 8
- Try 7.1: 7.1 * 7.1 = 50.41 (too high)
- Try 7.05: 7.05 * 7.05 = 49.7025 (close)
- So, √50 ≈ 7.05
6. Using Calculators
Modern calculators and software can easily find square roots. Simply enter the number and press the square root button (usually denoted as √ or with a function key).
7. Special Cases
- Perfect Squares: Numbers like 1, 4, 9, 16, 25, etc., have whole number square roots.
- Non-Perfect Squares: Numbers that do not have whole number square roots result in irrational numbers.
Understanding and using these methods will help you solve the square root of any number efficiently.

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is the inverse operation of squaring a number. For example, the square root of 9 is 3 because 3 multiplied by 3 equals 9.
Mathematically, the square root is represented by the radical symbol (√). For a number x, the square root is written as √x. The number under the radical symbol is called the radicand.
Here are some fundamental concepts related to square roots:
- Perfect Squares: Numbers like 1, 4, 9, 16, 25, etc., which are squares of integers, are called perfect squares. For example, 4 is a perfect square because it is 2 squared (2^2 = 4).
- Non-Perfect Squares: Numbers that are not perfect squares do not have integer square roots. For instance, the square root of 2 is an irrational number approximately equal to 1.414.
- Positive and Negative Roots: While every positive number has two square roots (one positive and one negative), the principal square root is the non-negative value. For example, both 3 and -3 are square roots of 9, but the principal square root is 3.
Let's consider an example to illustrate the concept:
Example: Find the square root of 16.
- We know that 16 is a perfect square.
- The number 4, when multiplied by itself, gives 16 (4 × 4 = 16).
- Thus, the square root of 16 is 4.
Square roots also apply to decimal numbers and fractions. For example, the square root of 0.25 is 0.5 because 0.5 multiplied by 0.5 equals 0.25.
In summary, the square root function is a fundamental mathematical operation with wide applications in various fields, including geometry, algebra, and real-world problem-solving.
Understanding Square Numbers
Square numbers are the result of multiplying an integer by itself. They are also known as perfect squares. For example, the square of 4 is calculated as follows:
Square numbers can be positive or negative because the product of two negative numbers is positive. Here are some examples:
\[3^2 = 3 \times 3 = 9\] \[(-3)^2 = (-3) \times (-3) = 9\] \[\left(\frac{5}{2}\right)^2 = \frac{5}{2} \times \frac{5}{2} = \frac{25}{4}\]
In general, a square number can be written as \(n^2\), where \(n\) is an integer. For example:
\[4^2 = 16\] \[(-6)^2 = 36\]
Square numbers have specific properties and applications, particularly in algebra, where they help in solving equations and understanding relationships between numbers. For instance, if \(x^2 = y\), then \(x = \sqrt{y}\) or \(x = -\sqrt{y}\).
The principal square root, denoted as \(\sqrt{y}\), refers to the non-negative square root of \(y\). For example:
\[\sqrt{25} = 5\] \[\sqrt{49} = 7\]
To further illustrate, the principal square root of a number is the one that is non-negative:
Understanding square numbers is crucial as they form the basis for more advanced mathematical concepts, including solving quadratic equations, understanding geometric shapes, and performing algebraic manipulations.
Square Roots: Basic Concepts
The square root of a number is a value that, when multiplied by itself, gives the original number. The symbol for the square root is √, known as the radical sign. For example, the square root of 9 is 3 because 3 × 3 = 9. This can be expressed as:
\(\sqrt{9} = 3\)
Here are some important concepts and properties of square roots:
- Every positive number has two square roots: one positive and one negative. For instance, the square roots of 25 are 5 and -5, because \(5^2 = 25\) and \((-5)^2 = 25\). However, by convention, √ refers to the principal (non-negative) square root.
- Square roots can be approximated using methods like Heron's method or a calculator for non-perfect squares.
- Square roots of fractions can be calculated by taking the square root of the numerator and the denominator separately. For example: \(\sqrt{\frac{25}{16}} = \frac{\sqrt{25}}{\sqrt{16}} = \frac{5}{4}\).
- Square roots follow the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\), which helps in simplifying expressions. For instance: \(\sqrt{36 \times 25} = \sqrt{36} \times \sqrt{25} = 6 \times 5 = 30\).
Here is a step-by-step example of solving a square root:
- Identify the number you want to find the square root of, say 16.
- Determine what number multiplied by itself gives 16. Here, 4 × 4 = 16.
- So, the square root of 16 is 4, which can be written as: \(\sqrt{16} = 4\).
For numbers that are not perfect squares, the square root can be approximated. For instance, the square root of 20 can be estimated as follows:
- Identify two perfect squares between which 20 lies. In this case, 16 (4²) and 25 (5²).
- Since 20 is closer to 16, start with an estimate of 4.5. Refine the estimate using a calculator or iterative methods like Heron's method.
Understanding these basic concepts about square roots is essential for solving more complex mathematical problems.
The Relationship Between Squares and Square Roots
Understanding the relationship between squares and square roots is fundamental in mathematics. A square number is the result of multiplying an integer by itself. For example:
In general, if n is an integer, then is a perfect square.
The square root is the inverse operation of squaring a number. It finds the original number that was squared to get a given square. For example:
Mathematically, if , then . The relationship can be summarized as follows:
| Number (x) | Square (x^2) | Square Root (√x^2) |
|---|---|---|
| 2 | 4 | 2 |
| 3 | 9 | 3 |
| 4 | 16 | 4 |
This relationship is crucial for understanding various mathematical concepts and solving equations involving square roots. For instance, knowing that helps in simplifying expressions and solving problems efficiently.
In summary, while squaring a number means multiplying it by itself, finding the square root involves determining which number, when squared, produces the given value. Both operations are inverse processes that highlight the intrinsic connection between squares and square roots.
Perfect Squares and Their Roots
Perfect squares are the squares of whole numbers. These numbers have special significance because their square roots are always whole numbers as well. Understanding perfect squares and their roots helps in simplifying and solving various mathematical problems.
Here is a list of perfect squares from 0 to 15:
- 02 = 0
- 12 = 1
- 22 = 4
- 32 = 9
- 42 = 16
- 52 = 25
- 62 = 36
- 72 = 49
- 82 = 64
- 92 = 81
- 102 = 100
- 112 = 121
- 122 = 144
- 132 = 169
- 142 = 196
- 152 = 225
The square root function is the inverse of squaring. This means if you have a perfect square, you can easily find its square root. For example, since 42 = 16, it follows that √16 = 4.
Here is a table showing perfect squares and their corresponding square roots:
| Number | Square | Square Root |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 4 | 2 |
| 3 | 9 | 3 |
| 4 | 16 | 4 |
| 5 | 25 | 5 |
| 6 | 36 | 6 |
| 7 | 49 | 7 |
| 8 | 64 | 8 |
| 9 | 81 | 9 |
| 10 | 100 | 10 |
| 11 | 121 | 11 |
| 12 | 144 | 12 |
| 13 | 169 | 13 |
| 14 | 196 | 14 |
| 15 | 225 | 15 |
Knowing the perfect squares and their roots can help in many areas of math, including solving quadratic equations, simplifying expressions, and more.
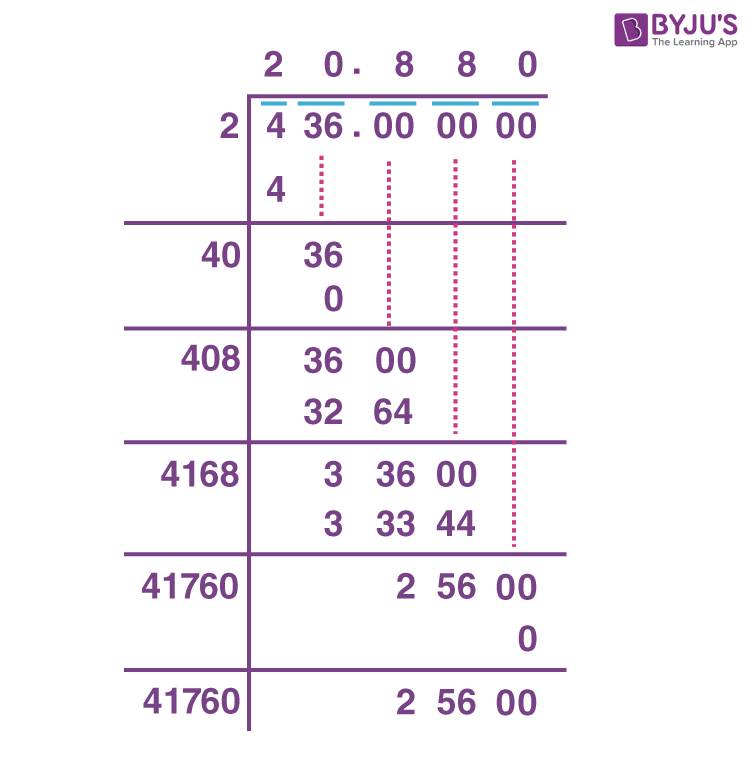
Calculating Square Roots of Non-Perfect Squares
Calculating the square root of non-perfect squares can be done using various methods. Here are the steps for some of the most commonly used methods:
Method 1: Long Division Method
Group the digits in pairs from the decimal point. If the number is whole, start grouping from the right. Add zeros if necessary.
Find the largest square number less than or equal to the first group. Write this number's square root as the first digit of the answer.
Subtract the square number from the first group and bring down the next pair of digits.
Double the current result, and write it down as a new divisor with a placeholder for the next digit.
Find a digit which, when added to the placeholder and multiplied by the resulting number, gives a product less than or equal to the current number. This digit becomes the next digit of the result.
Repeat the process until the desired accuracy is achieved.
For example, to find the square root of 2 using the long division method:
| Step | Explanation |
| 1 | Group digits: 2.00 (add decimal points) |
| 2 | Largest square less than 2 is 1 (1x1). Write 1 as the first digit. |
| 3 | Subtract 1 from 2, bring down 00 to get 100. |
| 4 | Double 1 to get 2. Find a digit such that 2d x d is less than or equal to 100. |
| 5 | The digit is 4 (24 x 4 = 96). Write 4 as the next digit. |
| 6 | Repeat the process with the new remainder. |
Method 2: Estimation and Averaging
Start with a rough estimate. For example, to find the square root of 20, note that it lies between 4 (since 42 = 16) and 5 (since 52 = 25).
Divide 20 by the estimate. Average the quotient and the estimate. For example, 20/4.5 = 4.44, and the average of 4.5 and 4.44 is approximately 4.47.
Repeat the process until the result is accurate enough.
Method 3: Newton's Method (Iterative Method)
Choose an initial guess for the square root (x0).
Use the formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \) where S is the number whose square root is desired.
Repeat until the difference between successive approximations is smaller than the desired accuracy.
For example, to find the square root of 20 using Newton's Method:
Start with an initial guess: x0 = 4.5
Apply the formula: x1 = 0.5 * (4.5 + 20/4.5) = 4.472
Repeat the process until convergence.
These methods provide systematic approaches to finding the square roots of non-perfect squares, ensuring accuracy through iterative steps.
Methods to Calculate Square Roots
Calculating the square root of a number can be done using several methods. Here, we will explore three primary methods: the prime factorization method, the long division method, and using a calculator.
Prime Factorization Method
This method works well for perfect squares. Follow these steps:
- Factor the number into its prime factors.
- Group the factors into pairs of identical numbers.
- Take one number from each pair and multiply them together.
For example, to find the square root of 144:
- Prime factors of 144: \( 144 = 2 \times 2 \times 2 \times 2 \times 3 \times 3 \)
- Group into pairs: \( (2 \times 2), (2 \times 2), (3 \times 3) \)
- Take one number from each pair and multiply: \( 2 \times 2 \times 3 = 12 \)
So, \( \sqrt{144} = 12 \).
Long Division Method
This method is useful for both perfect and non-perfect squares. Here’s a step-by-step guide:
- Group the digits of the number in pairs, starting from the decimal point.
- Find the largest number whose square is less than or equal to the first pair. Write this number as the divisor and the quotient.
- Subtract the square of the divisor from the first pair and bring down the next pair of digits.
- Double the quotient and write it as the new divisor, leaving a blank digit at the end. Find a digit to fill the blank such that when the new divisor is multiplied by this digit, the product is less than or equal to the current number.
- Repeat the process until all pairs of digits have been brought down.
For example, to find the square root of 20 using the long division method:
- Group digits: \( 20.000000 \)
- First pair: 20. Largest number whose square ≤ 20 is 4 (since \( 4^2 = 16 \)).
- Subtract: \( 20 - 16 = 4 \). Bring down next pair: 400.
- New divisor: \( 2 \times 4 = 8 \). Find a digit \( x \) such that \( 8x \times x \leq 400 \).
- Continue the process: the next digit is 5, so the divisor becomes 85 and \( 85 \times 5 = 425 \).
This continues until the desired accuracy is achieved. The result is approximately \( \sqrt{20} \approx 4.47 \).
Using a Calculator
Using a calculator is the simplest and fastest method:
- Enter the number for which you want to find the square root.
- Press the square root (√) button.
For example, to find the square root of 50:
- Enter 50 and press √.
- The display shows \( \sqrt{50} \approx 7.071 \).
Each of these methods provides a way to calculate square roots accurately, with the choice depending on the context and tools available.
Prime Factorization Method
The prime factorization method is a systematic way to find the square root of a number by expressing it as a product of its prime factors. Here’s a detailed step-by-step guide:
-
Factorize the Number into Prime Factors
Start by dividing the number by the smallest prime number (usually 2) and continue dividing the quotient by prime numbers until the quotient is a prime number. This process will give you the prime factors of the number.
Example: To factorize 72:
- 72 ÷ 2 = 36
- 36 ÷ 2 = 18
- 18 ÷ 2 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
Prime factors of 72 are: \(2^3 \times 3^2\)
-
Organize the Prime Factors into Pairs
Group identical prime factors into pairs. If a factor does not have a pair, it remains single.
Example: From \(2^3 \times 3^2\):
- Pairs: (2, 2), (2), (3, 3)
-
Multiply One Element from Each Pair
Select one prime from each pair and multiply them. Any unpaired prime factor remains under the square root.
Example: \(2 \times 3 = 6\) (with 2 remaining unpaired under the square root)
-
Calculate the Square Root
Multiply the results from the previous step and combine with any unpaired factors under the square root symbol.
Example: The square root of 72 is \(6\sqrt{2}\).
Examples
Example 1: Square Root of 144
- Prime factorize 144: \(144 = 2^4 \times 3^2\)
- Pairs: (2, 2), (2, 2), (3, 3)
- Multiply one from each pair: \(2 \times 2 \times 3 = 12\)
- Since all factors are paired, \(\sqrt{144} = 12\)
Example 2: Square Root of 200
- Prime factorize 200: \(200 = 2^3 \times 5^2\)
- Pairs: (2, 2), (5, 5), with 2 unpaired
- Multiply one from each pair: \(2 \times 5 = 10\)
- Square root: \(\sqrt{200} = 10\sqrt{2}\)

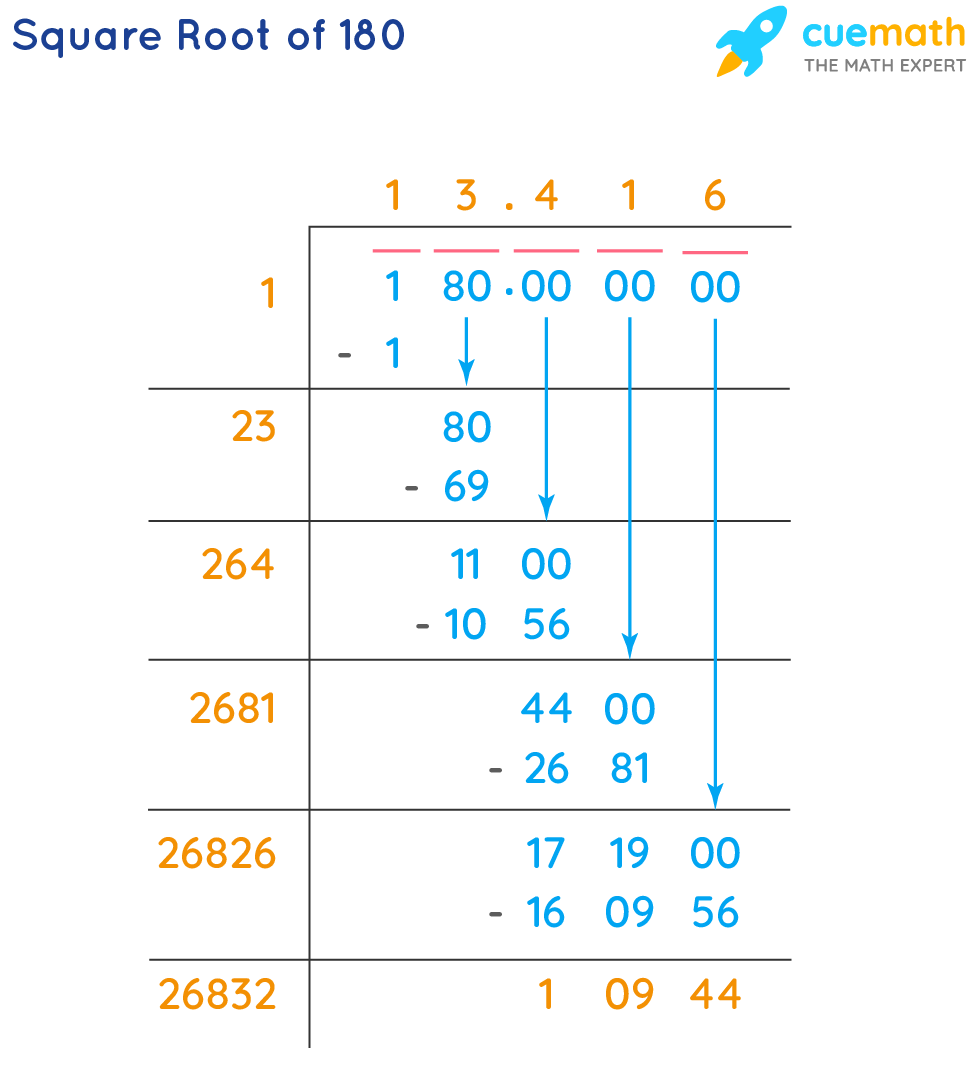
Long Division Method
The long division method is a systematic technique to find the square root of a number. This method is particularly useful for large numbers or for numbers that are not perfect squares. Here are the detailed steps:
-
Pair the Digits: Start by pairing the digits of the number from right to left. If the number has an odd number of digits, the leftmost digit will be unpaired. For example, to find the square root of 104976, we pair the digits as 10, 49, 76.
-
Find the Largest Integer: Find the largest integer whose square is less than or equal to the first pair or unpaired digit. Write this integer as the first digit of the quotient. Subtract the square of this integer from the first pair to get the remainder. In our example, the largest integer whose square is less than or equal to 10 is 3 (since 32 = 9). Write 3 as the first digit of the quotient and subtract 9 from 10 to get a remainder of 1.
-
Bring Down the Next Pair: Bring down the next pair of digits next to the remainder to form a new dividend. In the example, bring down 49 to get 149.
-
Double the Quotient: Double the quotient obtained so far (ignore the last digit) and write it as the new divisor with a blank digit. Find the largest digit to fill in the blank so that the product of the new divisor and this digit is less than or equal to the new dividend. Add this digit to the quotient and also to the divisor to update both. Subtract the product from the dividend to get a new remainder. For 149, double the quotient 3 to get 6_, find that 62 * 2 = 124 ≤ 149. Update quotient to 32 and divisor to 62.
-
Repeat the Process: Repeat the process of bringing down pairs of digits, doubling the quotient, and finding the appropriate digit until all pairs have been brought down and processed. For example, bring down 76, and so forth, until the remainder is zero or until you have reached the desired precision.
-
Handle Decimals: If you need more precision, after processing all the original pairs, add pairs of zeros to the dividend and continue the process. This will give the decimal places of the square root.
Let's illustrate this with an example:
- Pair the digits: 10, 49, 76.
- Find the largest integer for the first pair: 3 (32 = 9, remainder = 1).
- Bring down the next pair: 149.
- Double the quotient (3): 6_. Find 62 * 2 = 124. Update quotient to 32, remainder to 25.
- Bring down the next pair: 2576.
- Double the quotient (32): 64_. Find 644 * 4 = 2576. Update quotient to 324, remainder to 0.
Thus, the square root of 104976 is 324.
Using a Calculator for Square Roots
Calculating square roots using a calculator is straightforward and efficient. Here’s how you can do it:
- Turn on your calculator and make sure it’s set to the basic or scientific mode.
- Enter the number for which you want to find the square root.
- Press the square root (√) button. On most calculators, this is denoted as √ or sqrt.
- The result will appear on the screen. Ensure that your calculator displays the principal square root (non-negative root).
For example, to find the square root of 25:
| Step 1: | Turn on your calculator. |
| Step 2: | Enter 25. |
| Step 3: | Press the √ button. |
| Step 4: | The calculator displays 5 as the square root of 25. |
Using a calculator is especially useful for quickly obtaining accurate square root values, whether dealing with perfect squares or non-perfect squares.
Handling Decimal Numbers
Calculating the square root of decimal numbers can be straightforward if you follow these steps:
- Convert the Decimal to a Fraction:
Express the decimal as a fraction. For example, 0.25 can be written as \(\frac{25}{100}\).
- Simplify the Fraction:
Reduce the fraction to its simplest form. \(\frac{25}{100}\) simplifies to \(\frac{1}{4}\).
- Calculate the Square Root of the Numerator and Denominator Separately:
Find the square root of the numerator and the denominator separately. In this case, \(\sqrt{1} = 1\) and \(\sqrt{4} = 2\). Thus, \(\sqrt{\frac{1}{4}} = \frac{1}{2}\).
- Express the Result as a Decimal:
Convert the result back to decimal form. \(\frac{1}{2} = 0.5\).
Here’s an example to illustrate the process:
- Example: Find the square root of 0.81.
- Express 0.81 as a fraction: \(\frac{81}{100}\).
- Simplify the fraction: It's already in simplest form.
- Calculate the square root of the numerator and denominator:
\(\sqrt{81} = 9\) and \(\sqrt{100} = 10\). Thus, \(\sqrt{\frac{81}{100}} = \frac{9}{10}\).
- Express the result as a decimal: \(\frac{9}{10} = 0.9\).
For another method, consider the following steps:
- Square Root by Estimation:
- Find two perfect squares between which the decimal lies. For 0.81, it lies between 0.64 (\(0.8^2\)) and 1 (\(1^2\)).
- Estimate a value between the two perfect squares. In this case, 0.9 is a reasonable estimate since \(0.9^2 = 0.81\).
Using these methods can help simplify the process of finding the square root of decimal numbers.
Square Roots of Negative Numbers
When dealing with the square roots of negative numbers, we enter the realm of imaginary numbers. Imaginary numbers are essential in various fields of mathematics and engineering, despite their name suggesting otherwise. The imaginary unit is denoted by \( i \), where \( i \) is defined as the square root of -1, i.e., \( i = \sqrt{-1} \).
Understanding Imaginary Numbers
Imaginary numbers arise from the need to solve equations that involve the square root of negative numbers. For example, consider the square root of -9:
- \(\sqrt{-9} = \sqrt{9 \times -1} = \sqrt{9} \times \sqrt{-1} = 3 \times i = 3i\)
Here, \( 3i \) is the imaginary number result of \( \sqrt{-9} \).
General Rule
The general formula for the square root of any negative number can be written as:
\[\sqrt{-x} = i\sqrt{x}\]
Where \( x \) is a positive number. This means that the square root of a negative number is the product of \( i \) and the square root of the positive counterpart of that number.
Examples
| Expression | Solution |
|---|---|
| \(\sqrt{-4}\) | \(2i\) |
| \(\sqrt{-16}\) | \(4i\) |
| \(\sqrt{-25}\) | \(5i\) |
Applications of Imaginary Numbers
Imaginary numbers are used in various applications such as electrical engineering, signal processing, and control theory. For instance, in alternating current (AC) circuit analysis, complex numbers (which include imaginary numbers) are used to describe the phase difference between voltage and current.
Complex Numbers
Imaginary numbers can be combined with real numbers to form complex numbers. A complex number is expressed in the form \( a + bi \), where \( a \) and \( b \) are real numbers, and \( i \) is the imaginary unit. For example, \( 3 + 4i \) is a complex number.
Conclusion
Imaginary numbers might seem abstract at first, but they are incredibly useful in solving equations that have no real solutions and are applied extensively in various scientific and engineering disciplines.
Visualizing Square Roots
Visualizing square roots can greatly aid in understanding their concepts and properties. Here are several ways to visualize square roots:
-
Using a Number Line: Place the numbers on a number line and identify their square roots. For example, the square root of 4 is 2, which can be visualized as the distance from 0 to 2 on the number line.
-
Geometric Representation: Represent square roots as the side length of a square. For example, the square root of 9 is 3 because a square with side lengths of 3 units has an area of 9 square units.
-
Graphical Visualization: Use graphs to show the relationship between numbers and their square roots. The graph of the function \( y = \sqrt{x} \) helps illustrate how square roots grow as the numbers increase.
Here are some examples of square roots visualized using these methods:
| Number | Square Root | Visualization |
|---|---|---|
| 4 | \(\sqrt{4} = 2\) |  |
| 9 | \(\sqrt{9} = 3\) |  |
| 16 | \(\sqrt{16} = 4\) |  |
Additionally, using technology such as graphing calculators or computer software can help in visualizing square roots more interactively. Tools like sliders can demonstrate how the square root function behaves for different values of x.
Overall, visualizing square roots through these methods can make the abstract concept more tangible and easier to understand.
Practical Applications of Square Roots
Square roots are used in various fields and everyday situations. Here are some of the practical applications:
- Finance: In finance, square roots are used to calculate stock market volatility. The standard deviation, which measures the dispersion of stock returns, is the square root of the variance.
- Architecture: Architects use square roots to determine the natural frequency of structures like bridges and buildings to predict how they will respond to environmental factors such as wind or earthquakes.
- Science: Square roots are used in various scientific calculations, including the determination of the velocity of moving objects and the intensity of sound waves.
- Statistics: In statistics, square roots are used to calculate standard deviation, which indicates how much individual data points deviate from the mean of the data set.
- Geometry: Square roots are essential in geometry for calculating the sides of right triangles using the Pythagorean theorem, where the hypotenuse is found by taking the square root of the sum of the squares of the other two sides.
- Computer Science: In computer science, square roots are used in algorithms for encryption, image processing, and game physics. For example, encryption algorithms use modular arithmetic and square roots to generate secure keys.
- Navigation: Square roots are used in navigation to compute distances between points on a map or globe, which is essential for pilots and mariners in planning their routes.
- Electrical Engineering: Electrical engineers use square roots to calculate power, voltage, and current in circuits. These calculations are crucial for designing efficient electrical systems.
- Photography: In photography, the aperture of a camera lens, which controls the amount of light entering the camera, is expressed as an f-number. The area of the aperture is proportional to the square of the f-number.
- Cooking: When scaling recipes, the square root of the scaling factor is used to adjust the amount of ingredients, ensuring the right balance of flavors even when making larger batches.
- Computer Graphics: Square roots are used in 2D and 3D graphics applications to calculate distances between points or lengths of vectors, essential for rendering accurate images and animations.
These examples illustrate how fundamental square roots are to a variety of fields and everyday activities, demonstrating their importance beyond pure mathematics.
Fun Facts About Square Roots
Square roots are fascinating and come with several interesting facts that showcase their unique properties and applications in mathematics. Here are some fun facts about square roots:
- Imaginary Numbers: The square roots of negative numbers are not real; they are called imaginary numbers. For example, the square root of -1 is represented as \(i\), where \(i^2 = -1\).
- Irrational Numbers: The square root of 2 is an irrational number, approximately 1.41421. This means it cannot be expressed as a simple fraction.
- Historical Origins: The square root symbol (√) is believed to come from the letter "r", representing "radix" in Latin, meaning "root".
- Geometric Representation: Square roots can be visualized geometrically. For instance, the diagonal of a square with side length 1 is √2.
- Golden Ratio: The golden ratio, approximately 1.618, can be represented using square roots: \(\phi = \frac{1 + \sqrt{5}}{2}\).
- Perfect Squares: Numbers that are perfect squares have whole numbers as their square roots. For example, the square root of 16 is 4.
- Newton's Method: A quick way to approximate square roots is using Newton's method: \[A_{k+1} = \frac{1}{2} \left( A_k + \frac{N}{A_k} \right)\]. This iterative method converges rapidly to the square root of \(N\).
Below is a table of the first few perfect squares and their square roots:
| Number | Square Root |
|---|---|
| 1 | 1.000 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2.000 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3.000 |
| 10 | 3.162 |
Khám phá khái niệm căn bậc hai với Thầy J trong video này. Tìm hiểu cách tính căn bậc hai và ứng dụng của nó trong toán học.
Căn Bậc Hai Là Gì? | Toán Học với Thầy J
READ MORE:
Khám phá mẹo tính căn bậc hai nhanh chóng và hiệu quả trong video này. Học cách áp dụng các phương pháp đơn giản để giải quyết căn bậc hai của một số.
Mẹo Tính Căn Bậc Hai











