Topic how to solve a square root function: Discover the essential methods and techniques to solve square root functions with ease. This comprehensive guide provides a step-by-step approach, covering properties, domain and range, graphing, and practical examples. Perfect for students and enthusiasts aiming to master square root functions confidently and effectively.
Table of Content
- How to Solve a Square Root Function
- Introduction to Square Root Functions
- Properties of Square Root Functions
- Domain and Range of Square Root Functions
- Methods to Solve Square Root Equations
- Using the Square Root Property
- Examples and Practice Problems
- Common Mistakes and Troubleshooting
- Applications of Square Root Functions
- YOUTUBE: Học cách giải các phương trình căn bậc hai trong video này. Xem ngay để nắm bắt các kỹ năng quan trọng trong toán học!
How to Solve a Square Root Function
Solving square root functions involves isolating the square root term, squaring both sides to remove the square root, and then solving the resulting equation. Here's a step-by-step guide:
Steps to Solve Square Root Equations
-
Isolate the Square Root: Move all other terms to the opposite side of the equation to isolate the square root term.
Example: \( \sqrt{5x + 6} = 9 \)
-
Square Both Sides: Square both sides of the equation to eliminate the square root.
\( (\sqrt{5x + 6})^2 = 9^2 \)
\( 5x + 6 = 81 \)
-
Solve the Resulting Equation: Solve the resulting equation using algebraic methods.
Subtract 6 from both sides: \( 5x = 75 \)
Divide by 5: \( x = 15 \)
-
Check the Solution: Substitute the solution back into the original equation to verify it.
\( \sqrt{5(15) + 6} = 9 \)
\( \sqrt{75 + 6} = 9 \)
\( \sqrt{81} = 9 \)
Since 9 = 9, the solution \( x = 15 \) is correct.
Example Problems
Example 1: Simple Square Root Equation
Solve \( \sqrt{2x + 3} = 7 \).
- Square both sides: \( (2x + 3) = 7^2 \)
- Simplify: \( 2x + 3 = 49 \)
- Isolate x: \( 2x = 46 \)
- Solve: \( x = 23 \)
Example 2: Square Root Function
Consider the function \( f(x) = 2\sqrt{x + 1} + 7 \). Find the output for \( x = 0, 3, 8 \).
- For \( x = 0 \): \( f(0) = 2\sqrt{0 + 1} + 7 = 9 \)
- For \( x = 3 \): \( f(3) = 2\sqrt{3 + 1} + 7 = 11 \)
- For \( x = 8 \): \( f(8) = 2\sqrt{8 + 1} + 7 = 13 \)
Graphing Square Root Functions
Graphing square root functions involves plotting points and understanding transformations. The parent square root function is \( f(x) = \sqrt{x} \), which can be translated, dilated, and reflected to form \( f(x) = a\sqrt{b(x - h)} + k \).
- Domain: The set of all possible input values.
- Range: The set of all possible output values.
- Example: For \( f(x) = 2\sqrt{x + 1} + 7 \), the domain is \( x \ge -1 \) and the range is \( y \ge 7 \).
By following these steps and examples, you can effectively solve and graph square root functions. Practice with various problems to enhance your understanding.

READ MORE:
Introduction to Square Root Functions
Square root functions are a type of radical function where the variable is under the square root symbol. The general form of a square root function is \( f(x) = \sqrt{x} \). These functions are crucial in various fields such as physics, engineering, and finance, as they describe phenomena that grow at a decreasing rate. Understanding square root functions involves exploring their properties, domains, ranges, and graphical representations.
Square root functions are unique because they are defined only for non-negative values of \( x \), given that the square root of a negative number is not a real number. This leads to the domain of \( f(x) = \sqrt{x} \) being \( [0, \infty) \). Similarly, since the output of \( \sqrt{x} \) is always non-negative, the range of the function is also \( [0, \infty) \).
Here are some fundamental properties of square root functions:
- Domain: \( [0, \infty) \)
- Range: \( [0, \infty) \)
- The graph of \( f(x) = \sqrt{x} \) is a curve that starts at the origin (0,0) and increases slowly to the right.
- It is an increasing function, meaning that as \( x \) increases, \( f(x) \) also increases.
To solve square root functions, one often isolates the square root on one side of the equation and then squares both sides to eliminate the square root. Here’s a simple example:
- Consider the equation \( \sqrt{x + 3} = 5 \).
- First, square both sides: \( (\sqrt{x + 3})^2 = 5^2 \) to get \( x + 3 = 25 \).
- Then, solve for \( x \): \( x = 25 - 3 \), which simplifies to \( x = 22 \).
Graphing square root functions involves plotting points and drawing a smooth curve through them. For example, to graph \( f(x) = \sqrt{x - 2} + 3 \), compute and plot several points by substituting values of \( x \) and finding corresponding \( y \)-values.
Properties of Square Root Functions
The square root function, typically represented as \( f(x) = \sqrt{x} \), has several important properties:
- Domain: The domain of \( f(x) = \sqrt{x} \) is \( [0, \infty) \), meaning it includes all non-negative real numbers. This is because the square root of a negative number is not defined in the set of real numbers.
- Range: The range of \( f(x) = \sqrt{x} \) is also \( [0, \infty) \), which includes all non-negative real numbers. As \( x \) increases, \( \sqrt{x} \) also increases.
- Intercepts: The function \( f(x) = \sqrt{x} \) has a y-intercept at (0,0). There are no x-intercepts as the function never crosses the x-axis for positive values.
- Behavior: The square root function is always increasing; as \( x \) increases, \( \sqrt{x} \) also increases. However, it increases at a decreasing rate, meaning it gets flatter as \( x \) gets larger.
- End Behavior: As \( x \) approaches infinity, \( \sqrt{x} \) also approaches infinity. As \( x \) approaches zero from the right, \( \sqrt{x} \) approaches zero.
- Critical Points: The function has a critical point at (0,0), where it changes from not defined to defined and starts increasing.
- Symmetry: The square root function is not symmetric. It does not exhibit symmetry about the y-axis or the origin.
- Continuity: The function \( f(x) = \sqrt{x} \) is continuous for all \( x \) in its domain. There are no breaks, holes, or jumps in its graph.
These properties help in understanding the behavior of the square root function and in solving equations involving square roots.
Domain and Range of Square Root Functions
The domain and range of square root functions are essential aspects to understand their behavior. Let's explore them in detail:
Domain
The domain of a square root function is the set of all possible input values (x-values) that produce real numbers as outputs. For the function \( f(x) = \sqrt{x} \), the domain is all non-negative real numbers:
\[
\text{Domain} = \{ x \in \mathbb{R} \mid x \geq 0 \}
\]
In general, for a function of the form \( f(x) = \sqrt{g(x)} \), the domain is determined by setting the expression inside the square root greater than or equal to zero:
\[
g(x) \geq 0
\]
Range
The range of a square root function is the set of all possible output values (y-values) that the function can produce. For the function \( f(x) = \sqrt{x} \), the range is all non-negative real numbers:
\[
\text{Range} = \{ y \in \mathbb{R} \mid y \geq 0 \}
\]
In general, the range of \( f(x) = \sqrt{g(x)} \) is determined by considering the output values for the domain values:
\[
\text{Range} = \{ y \in \mathbb{R} \mid y \geq 0 \}
\]
Examples
- For \( f(x) = \sqrt{x-2} \):
- Domain: \( x-2 \geq 0 \) ⟹ \( x \geq 2 \)
- Range: \( y \geq 0 \)
- For \( f(x) = \sqrt{9-x^2} \):
- Domain: \( 9-x^2 \geq 0 \) ⟹ \( -3 \leq x \leq 3 \)
- Range: \( 0 \leq y \leq 3 \)
Understanding the domain and range of square root functions helps in graphing and solving equations involving these functions.
Methods to Solve Square Root Equations
Solving square root equations involves several methods. Below are the detailed steps:
-
Isolate the Square Root Term:
Ensure that the square root term is by itself on one side of the equation.
-
Square Both Sides:
Eliminate the square root by squaring both sides of the equation. For example, if you have \(\sqrt{x} = 3\), square both sides to get \(x = 9\).
-
Simplify the Resulting Equation:
After squaring both sides, simplify the equation to solve for the variable.
-
Check for Extraneous Solutions:
Substitute the solutions back into the original equation to verify they are valid, as squaring both sides can introduce extraneous solutions.
Here are some examples to illustrate these methods:
-
Example 1:
Solve \(\sqrt{x} + 2 = 5\):
- Isolate the square root: \(\sqrt{x} = 3\)
- Square both sides: \(x = 9\)
- Check: \(\sqrt{9} + 2 = 5\), which is true, so \(x = 9\) is a valid solution.
-
Example 2:
Solve \(\sqrt{2x + 3} = x - 1\):
- Square both sides: \(2x + 3 = (x - 1)^2\)
- Expand and simplify: \(2x + 3 = x^2 - 2x + 1\)
- Rearrange to form a quadratic equation: \(x^2 - 4x - 2 = 0\)
- Solve the quadratic equation using the quadratic formula: \(x = \frac{4 \pm \sqrt{16 + 8}}{2} = 2 \pm \sqrt{6}\)
- Check both solutions in the original equation to confirm validity.
By following these steps, you can systematically solve square root equations effectively.

Using the Square Root Property
The Square Root Property is a useful tool for solving quadratic equations of the form \(x^2 = k\), where \(k\) is a constant. This method involves isolating the quadratic term and then applying the property to find the solutions. Here are the steps to solve an equation using the Square Root Property:
- Isolate the quadratic term: Ensure that the quadratic term is by itself on one side of the equation. For example, if the equation is \(x^2 - 25 = 0\), add 25 to both sides to get \(x^2 = 25\).
- Apply the Square Root Property: According to the Square Root Property, if \(x^2 = k\), then \(x = \pm \sqrt{k}\). So for the equation \(x^2 = 25\), the solutions are \(x = \pm \sqrt{25}\), which simplifies to \(x = 5\) and \(x = -5\).
- Simplify the radical (if needed): In some cases, the value under the square root may not be a perfect square. For example, if \(x^2 = 7\), then \(x = \pm \sqrt{7}\). Since \(\sqrt{7}\) cannot be simplified further, the solutions remain as \(x = \sqrt{7}\) and \(x = -\sqrt{7}\).
- Check the solutions: Substitute the solutions back into the original equation to verify their correctness. For instance, substituting \(x = 5\) into \(x^2 - 25 = 0\) gives \(25 - 25 = 0\), which is true. Similarly, substituting \(x = -5\) gives the same result.
Let's look at a detailed example:
| Equation: | \(x^2 - 50 = 0\) |
| Step 1: | Isolate the quadratic term: \(x^2 = 50\) |
| Step 2: | Apply the Square Root Property: \(x = \pm \sqrt{50}\) |
| Step 3: | Simplify the radical: \(x = \pm \sqrt{25 \cdot 2} = \pm 5\sqrt{2}\) |
| Step 4: | Check the solutions by substituting back into the original equation:
|
Thus, the solutions to the equation \(x^2 - 50 = 0\) are \(x = 5\sqrt{2}\) and \(x = -5\sqrt{2}\).
The Square Root Property is particularly helpful for equations where the quadratic term is easily isolated and the constant term is not a perfect square, allowing for a straightforward solution process.
Examples and Practice Problems
1. Solve the equation \( \sqrt{x+5} = 3 \).
- Start with the equation \( \sqrt{x+5} = 3 \).
- Square both sides to eliminate the square root: \( x + 5 = 9 \).
- Solve for \( x \): \( x = 4 \).
2. Solve the inequality \( \sqrt{2x-1} \geq 3 \).
- Write the inequality \( \sqrt{2x-1} \geq 3 \).
- Square both sides to eliminate the square root: \( 2x - 1 \geq 9 \).
- Add 1 to both sides: \( 2x \geq 10 \).
- Divide both sides by 2: \( x \geq 5 \).
3. Solve the system of equations:
\[
\begin{cases}
\sqrt{y} = 4 \\
y - 5 = 3
\end{cases}
\]
- Solve \( \sqrt{y} = 4 \) to find \( y = 16 \).
- Use \( y - 5 = 3 \) to verify \( y = 8 \).
4. Simplify and solve the expression \( \sqrt{a^2 + 2a + 1} \) where \( a = 2 \).
- Substitute \( a = 2 \) into the expression: \( \sqrt{2^2 + 2 \cdot 2 + 1} \).
- Simplify under the square root: \( \sqrt{4 + 4 + 1} = \sqrt{9} = 3 \).
Common Mistakes and Troubleshooting
1. Forgetting to check for extraneous solutions, especially after squaring both sides of a square root equation.
2. Incorrectly applying the square root property by missing possible solutions or misidentifying valid domains.
3. Misinterpreting the domain and range restrictions of square root functions, leading to incorrect solutions.
4. Using incorrect algebraic manipulations when solving square root equations, such as incorrect signs or operations.
Applications of Square Root Functions
1. Calculating distances in physics and engineering, where distance is often represented by the square root of sums of squares.
2. Modeling financial growth or decay processes using square root functions to understand rates of change.
3. Estimating error margins in statistical analysis, where square roots are used to calculate standard deviations.
4. Designing parabolic shapes in architecture and art, utilizing square roots to determine curve parameters.
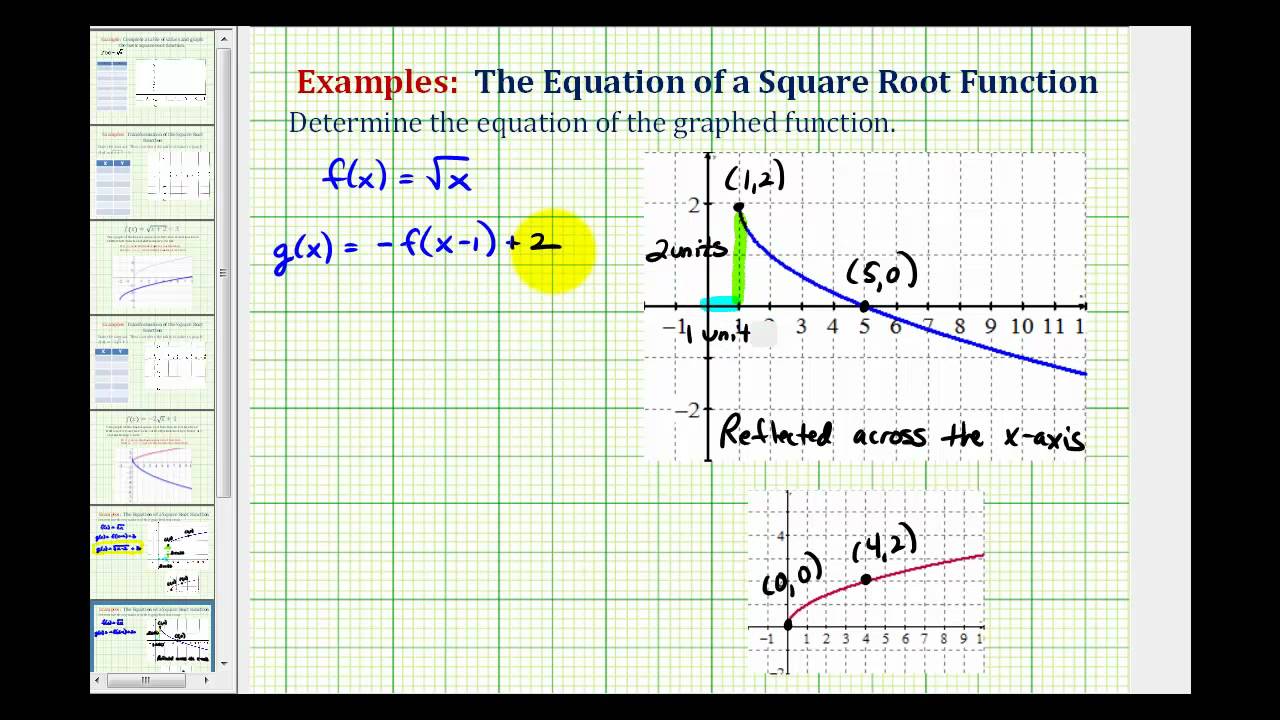
Học cách giải các phương trình căn bậc hai trong video này. Xem ngay để nắm bắt các kỹ năng quan trọng trong toán học!
Học cách giải phương trình căn bậc hai | Video hướng dẫn
READ MORE:
Học cách tìm miền xác định và viết trong dạng khoảng của hàm căn bậc hai trong video này. Xem ngay để nắm bắt các kỹ năng quan trọng trong toán học!
Tìm miền xác định và viết trong dạng khoảng của hàm căn bậc hai